一种自适应搜索的足球机器人定位方法

彭为微,　赵逢禹

(1.上海理工大学 医疗器械与食品学院,上海　200093; 2.上海理工大学 光电信息与计算机工程学院,上海　200093)



一种自适应搜索的足球机器人定位方法

彭为微1,赵逢禹2

(1.上海理工大学 医疗器械与食品学院,上海200093; 2.上海理工大学 光电信息与计算机工程学院,上海200093)

摘要：基于目前结构环境下的机器人定位问题,将机器人定位的概率问题转换为有限空间范围内的极小值搜索问题,实现了一种新的基于机器自学习的搜索方法.为了保证定位的实时性与定位精度,提出了一个能自动调整搜索步长的自适应搜索算法,解决了RoboCup中型组足球机器人的自定位问题,并在实际环境中完成了算法有效性测试.

关键词：自定位; 全向移动机器人; 全景成像; 扩展卡尔曼滤波器; 自适应搜索

机器人自定位问题作为移动机器人自主化、智能化研究中最为基础的问题,由于受到外界环境的复杂性、计算机资源的有限性,以及噪声和干扰的影响,一直是智能移动机器人领域研究的一个重点.

机器人自定位技术作为新的研究热门领域,自提出以来涌现了许多种方法.例如,纯粹利用编码器和陀螺仪的航迹推断算法[1],利用图像识别的几何定位方法[2].但是,由于基于航迹推断的方法存在无法避免的累积误差,而图像的几何定位方法对外界环境的适应性较差,且存在难以满足精度和实时性要求的问题,所以,这些方法在实际中未能得到广泛的应用.

目前,基于贝叶斯滤波理论的概率方法是解决机器人自定位问题的主流方法,在具体的实际应用中可采用多种不同的实现方式,其中,最有代表性的方法为基于贝叶斯估值理论的卡尔曼滤波器.卡尔曼滤波器提供了一种以最小均方差来估计机器人位姿信息的有效的递归计算方法,但是,由于其数学模型自身的局限性,卡尔曼滤波器也存在诸多不足.例如:a.起始姿态必须是已知且满足高斯分布;b.不能从跟踪失败中恢复过来,无法避免机器人定位的“绑架问题”;c.不能处理多峰分布时的定位问题.

由于卡尔曼滤波器模型本身的局限性,近几年,一种基于粒子滤波的方法被应用于足球机器人的定位[3-4],该方法又称为蒙特卡洛算法,其基本思想是采用带有权重的粒子的集合来表示对系统状态的估计,并通过序贯权重采样法来更新粒子集合.传统的粒子滤波的定位方法也存在其局限性,其中的粒子点数量直接影响了定位算法的复杂度和效果,因此，其定位精度和计算效率是相互矛盾的.

自定位算法作为足球机器人研究中最为重要和基础的组成部分,不仅估算出当前机器人在场地中实时的位置和朝向,同时也为移动物体的速度估计提供了计算基础,以便决策模块能对下一步动作作合理的规划,所以,自定位算法的实时性和定位精度显得尤为重要.

传统的粒子滤波算法的大量时间用于计算权重已经较低的粒子,而这些粒子对最终的定位效果的贡献其实已经非常小,为了避免这种多余的计算,很多学者提出了不同的解决办法.例如,文献[5]提出的对粒子群进行速度与位置变更的方法.本文提出了一种新的基于机器自学习的搜索方法,其基本思想是根据前几次搜索计算的结果自动修正搜索步长,在保证实时性的同时又保证了搜索精度.其本质可看作一个可以“移动”的粒子,其移动的步长来源于前几次学习的结果.由于不需要对粒子数量的约束,且当误差较大时,自适应算法会自动增加搜索步长,避免了粒子滤波器中粒子数量过少导致的“粒子贫乏”现象.另外,由于只采用了一个可移动的粒子,极大地降低了对计算机内存容量的要求,同时也避免了粒子数量过多而造成的计算量大、无法保证实时性的问题.此方法在解决了“粒子贫乏”的基础上,还避免了估算精度和算法效率难以兼顾的情况.

为了提高整体系统的计算频率,本文进一步提出了一种适合结构环境中的观测模型的计算方法,通过对相互独立的特征点进行聚合,将弱特征聚合为强特征点,从而在提高计算效率的同时,最大程度地避免了外界环境及图像处理中产生的误差对整体系统的影响.

1观测模型的计算方法

1.1成像系统

机器人的图像传感器大都基于小孔成像原理,成像效果好,但往往视野较窄,即使是鱼眼镜头,也存在图像扭曲程度过大且成像的角度只能在180°左右的问题.由于机器人运动速度较快(2～3m/s),且运动过程中常伴有自转,即使采用云台的方式,也难免会有拖影现象,且无法避免图像拼接难以匹配的问题.而对于中型组的足球机器人,如果视野被其他机器人遮挡,不能在比赛过程中实时360 °观察周围情况,机器人就无法确定自己的位姿.所以,在本实验机器人上采用了一种全景图像采集装置,相机并不直接对外成像,而是通过采集双曲反光镜反射的信息来获得外界360 °的环境信息,如图1所示,其主要结构分为三部分:短焦相机、双曲反光镜和支撑装置.

现介绍全景视觉系统的设计参数(安装位置为机器人顶部,距离地面高度为1m).

a. 视距范围:机器人周围5m以内清晰成像；

b. 视野范围:水平方向360 °,垂直方向5～80 °.

在实验场地的成像效果如图2所示.

摄像头的实际成像平面的图像来自场景的光线经过反射镜反射后在CCD(图像控制器)平面内的成像,并非双曲面反射全景成像系统的透视像.为了求取成像中的像点对应水平方向上的真实物体的位置(物点),根据设计的双曲镜面,可以用参数方程表示二次曲线.

式中:e为离心率;p为二次曲线的焦距；t为变量;r(t)为二次曲线.

图1　全景成像装置

图2　全景成像图

当e>1时,该方程表示双曲线,双曲面反射镜上点的坐标

式中:z(t)为径向坐标;r(t)为镜像坐标.

由图3可知,反射光线的方向向量

设镜面的法向向量为N(t),根据反射定律,得出入射光线的方向向量

虽然单目全景视觉系统无法得到深度信息,但在已知反射镜头的安装高度和入射光线的方向向量的情况下,即可求出在同一水平面上物点相对机器人的水平距离d.

式中:Z为双曲镜面距离地面的安装高度.

1.2特征点选取

近年来,针对RoboCup中型组足球机器人的定位问题,在定位时采用的特征点主要有以下3种:

a. 提取黄球门、蓝球门、立柱等特殊物体作为特征点,从而实现几何三角定位[6].

b. 通过Hough变换等方法来提取场地白色标志线组成的特殊几何形状,从而实现集合定位[7].

c. 提取场地白线上的白点作为特征点[8].

早期采用黄球门、蓝球门、立柱等特殊的地标点作为特征点的定位方法[9],其定位精度差,容易受到障碍物遮挡,加上现阶段中型组的比赛场地已经取消了类似的标志物,所以,此类方法已经不再适用,而且由于比赛场地的扩大,基于主动型传感器(激光测距仪和声纳等传感器)的定位方法[10-11]也不再适用.

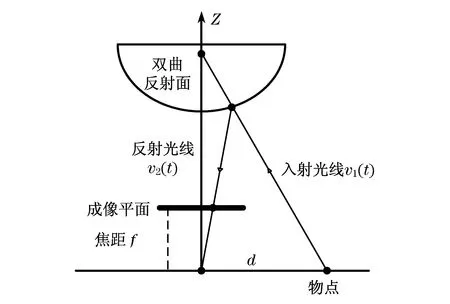
图3　双曲反射镜成像光路图

中型组比赛场地的简化,加上场地周围观众干扰等不确定性,使机器人定位非常容易受到外界因素的干扰；针对这种结构环境下的定位问题,依靠场地的尺寸和白线是唯一相对固定的条件.本文在图像处理过程中,选取白线作为参考点.

在以往采用白线作为特征点识别的方法中,往往倾向于利用图像内容中容易确定的强特征点,如角点、直线交叉点、中场的圆形等[12].这类特征点的优点是比较直观和方便理解,但针对这类区域特征点的计算方法往往需要借助图像分割算法,如Hough变换等.而这类算法的计算效率偏低,加上实际图像中经常因为遮挡导致数据缺失且包含噪声,所以,在实际的应用中很难保证识别的稳定性和实时性.

为了避免强特征点在识别过程中计算效率低、关键点被遮挡时无法正确识别的问题,本文提出将直线上的点作为观测模型计算的特征点.不同于角点、直线交叉点等强特征点,边线上单独的每个点虽然相互独立,但将相互独立的弱特征通过投票的机制聚合在一起时,便构成了强特征点,即使局部被遮挡或存在外部噪声时,也不会对整体的识别效果造成太大的影响.

为了提取边线上的白色特征点,如果对图像中的每个点都进行分析,则计算量太大(640×480=307 200个像素),且会提取出很多重复的特征点.在实际的计算中,结合全景成像的特点,采用扫描线的方式提取特征点[13],扫描线采用自机器人中心放射状的射线,如图4所示.

图4　放射状扫描线

特征点提取的方式为在扫描线上白色区域的中间点,且白色区域的两端都为绿色区域,如图5所示.图6给出了图5中特征点的局部放大图.

图6　扫描线与特征点的局部放大图

1.3地图模型的建立

作为结构环境下的机器人定位方法,首先需要建立场地的地图数据.在移动机器人定位中采用的地图的表示方法主要有4种:拓扑图、特征图、网格图和直接表征法.

由于中型组足球机器人比赛的场地尺寸已知,且观测模型的特征点已明确,故在直接表征法的基础上对其进行改进,地图的建立方法如下:

a. 以RoboCup中型组机器人真实比赛的场地尺寸建立模型,以场地上的白线作为标记物.

b. 以10cm的间距遍历场地中的所有位置,假设该特征点的质量为1,所有白线的质量为1,通过万有引力公式计算两物体之间的引力

F=GmM/r2

式中:G为引力常量;m,M分别为两物体的质量;r为两物体距离.

场地上所有线段对该特征点的引力的作用结果为一个合力,其结果用矢量表示.F的值越小,表示该点的误差值越大;反之越小.因为,这部分的计算量比较大且不会发生变化,所以,在实际的运用中，将它作为标定数据存放在内存中供查表使用,以提高计算速度.为了提高定位精度,场地边线外1m也进行计算,实际遍历区间为(18+2)×(12+2)m.

1.4观测模型的计算

在地图模型已知的情况下,每当捕获到新的图像信息后,首先提取白线上的特征点(参见图6),然后将识别到的每个特征点代入公式中进行计算,将特征点从机器人的相对坐标系转换到世界地图模型中的全局坐标系下,其转换式为

(1)

式中:si代表特征点在在机器人相对坐标系下的位置(X′,Y′);P点代表机器人在全局坐标系下的位置(X″,Y″);角度θ代表机器人当前的姿态;R为机器人在全局坐标下的位置.

从而可以将特征点在机器人相对坐标系下的(X′,Y′),通过坐标系旋转式,转换为特征点在全局坐标下的坐标(X,Y),其计算式即为

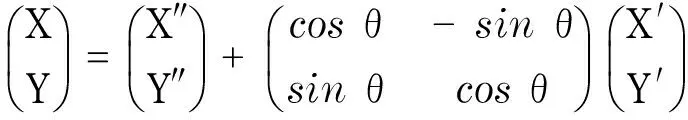
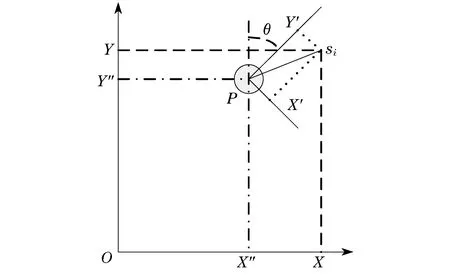
图7　机器人坐标特征点向全局坐标变换

当特征点转换到全局坐标系后,理论上所有的特征点都应该位于白线上且完全吻合,但是,由于机器人在运动过程中可能受到碰撞,其真实位置与姿态同理论值存在差异,将图像识别的特征点转换到全局坐标系后,都会存在一定的偏差.所以,将特征点到地图模型上最近白线的最小距离值(标量),作为该特征点的观测误差值.图8中的黑点表示特征点,黑线表示特征点到白线的距离,即特征点观测模型和世界模型间的误差值.

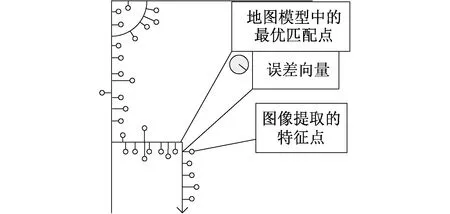
图8　计算出的特征点坐标

为了尽量减少识别错误点对定位效果的影响,在计算时,对距离白线越远的特征点Ri,采用的可信度越低；反之,越近的特征点,其可信度越高.误差值ε的计算公式为

(2)

式中:C取常数250;di为特征点Ri在地图模型中距离白线最短的距离.

误差值可看作是该特征点对当前机器人位置的一次投票.综合考虑所有的特征点投票,将其所有的误差值进行累加计算.

(3)

E可作为当前机器人位姿相对观测模型的一个评估值.该误差值越小,说明机器人在该位置的可能性越大；反之则可能性越小.相对于采用强特征进行识别并定位的方法[14-15],此方法将多个相互独立的弱特征聚合为强特征,在图像被遮挡或局部特征提取错误的情况下,不会导致整体系统计算失效,极大地提高了容错性,其计算量相对于特征点的数量也仅仅成线性比例关系,该方法在数量计算及速度上有非常大的提升.

2自适应搜索算法

机器人自定位的问题,可以转换为假设机器人在场地上的不同位置,计算在该位置的误差值,通过计算找到误差最小的位置,即为机器人当前所在概率最高的位置.从而将机器人自定位问题转换为计算图中误差最小位置的问题.该问题最简单的方法就是直接对场地上所有机器人的位置遍历计算后寻找最小值,但是,在实际操作中,由于机器人姿态由位置(X″,Y″)和姿态θ(因为机器人在平面上移动,所以这里的姿态代表机器人的转动角度信息)3个参数组成,如果在三维的环境下进行搜索,计算量会以几何倍数递增,例如:以X″,Y″最小搜索步长10cm,θ最小搜索步长1°为例,每次定位所需要的计算次数为(1 800/10)(1 200/10)(360/1),共7 776 000次,这么大的计算量很难达到实时性的要求.在实际应用中,为了平衡精度和实时性的矛盾,通常采用扩展卡尔曼滤波粒子滤波等方法来减少计算量,但都有不可避免的局限性.本文提出另一种求解方法,即将机器人自定位的问题转换为数值计算中求极大极小值的问题,从而避免了以往方法的局限性,其计算方法为

(4)

式中,n为特征点的数量.

在数学模型中,求解这类极大极小值问题的方法有很多,如爬山、模拟退火等方法,但在计算速度和精度上很难有一个很好的取舍.例如,当搜索范围小时,虽能很好地保证定位精度和实时性,但计算的结果容易陷入局部极小位置,导致出现粒子滤波中“粒子贫乏”问题.如果增大搜索的范围,又不能保证实时性.如果增加搜索步长,又会导致定位精度不能满足要求.为了解决采用固定步长无法同时满足精度和计算效率的问题,本文提出了一种基于机器自适应搜索的机器人定位算法.

将第t步搜索的步长定义为w(t),为了达到步长自适应调整的目的,下次搜索的步长不仅依靠学习率,而且还结合了前几次的计算结果来进行调整,这样就可以达到当目标偏离较远时,搜索步长会快速增加以期最快速度接近目标,当较接近搜索目标时,会在目标区域附近震荡,逐渐减小步长,以期最大程度接近目标.

为了达到搜索步长学习的目的,引入一个可变因子Δ来计算下一次的步长w(t+1),其更新的规则不仅仅依赖全局学习率η,而且还和前次学习的偏导数Δ(t-1)有关,计算公式为

全局学习率η的取值不依赖于前次搜索的结果,而取决于上次定位的偏差值.若前次定位的偏差越小,则η的取值越小,反之则越大,其计算方法为

式中:K为设定参数,用以满足0<η-<1<η+的约束条件;η+为误差变小时的正向学习率;η+-为误差变大时的逆向学习率.

当可变因子计算完成后,则可以计算步长的调节率Δw(t),计算公式为

最后即可得到下次采用的步长w(t+1),更新规则为

但是,会有一种意外情况,如果偏导数w(t-1)为负值时,及前次步长过大,则有可能会“冲过”目标点,从而错失最佳的匹配位置,所以,下次搜索的步长必须具有方向性,从而能够进行反向的调节,其计算方法为

3测试效果

针对自适应搜索算法和粒子滤波算法,在实际场地进行测试(18m×12m),直径为50cm的机器人,计算平台为P2.4双核CPU,1G内存,机器人从点A以1.5m/s的速度移动到点B,然后移动到点C,再回到点A作为一次测试样本.同时在运行过程中以激光测距设备实时保存机器人的位姿信息,作为算法定位效果对比的标准数据信息.图9表示机器人测试时的移动轨迹.

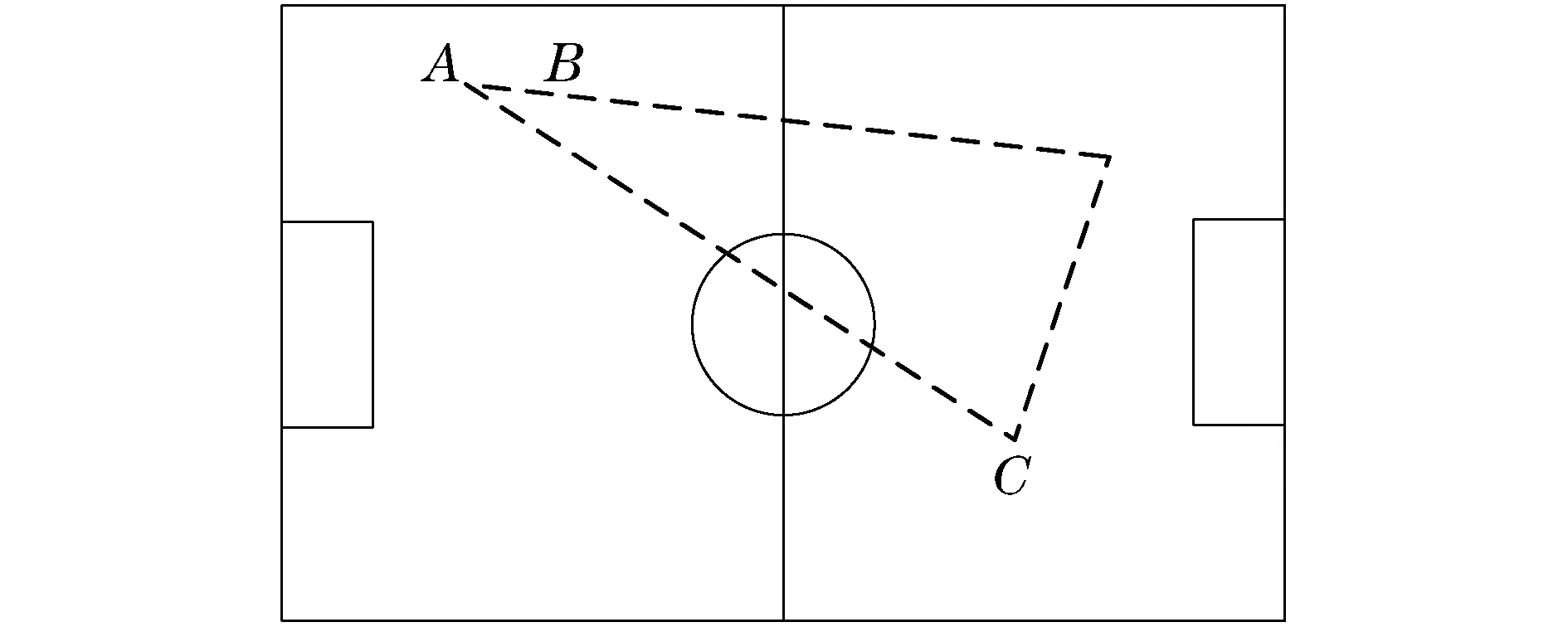
图9　机器人移动路径图

在同样的计算耗时(5ms)的情况下,粒子滤波方法中,粒子的数量不能大于50个,表1以50个粒子数量及150个粒的粒子滤波方法同自适应搜索算法的定位效果(平均误差)进行了对比,误差单位为ms.

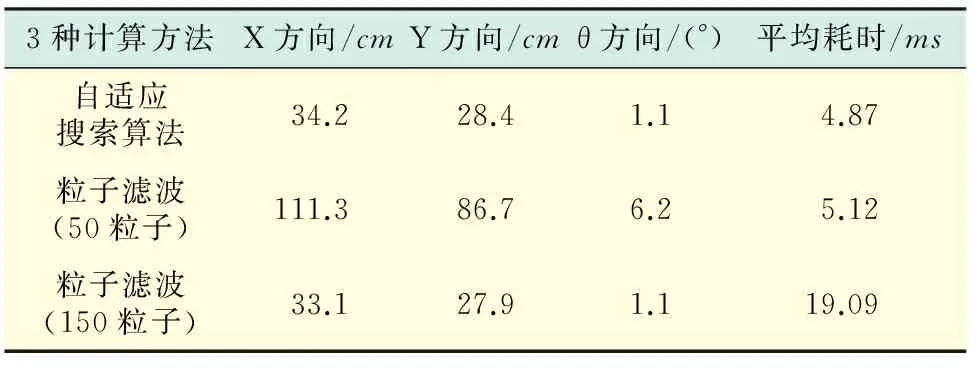
表1　定位精度和耗时对比

从表1看出,当粒子数量较少时(50个)时,计算的平均耗时都在5ms左右时,粒子滤波算法的定位精度远远低于自适应搜索算法的定位精度,其最大误差值可达111.3cm及6.2°,远大于自适应搜索算法的34.2cm和1.1°.当增加粒子数量到150个时,定位精度接近自适应搜索算法的定位精度,但计算时间却大幅增加,平均耗时达到19.09ms,远大于自适应搜索算法的4.87ms.

4结束语

基于粒子滤波的机器人自定位方法中,候选粒子的个数是个关键问题,它影响到机器人自定位的精度和算法消耗的时间,并且无法调和.相对于采用粒子滤波的定位方法,自适应搜索的定位方法在保证满足RoboCup中型组足球机器人定位精度要求的同时,极大地提高了计算效率.

参考文献：

[1]董晓杰,陈启军.卡尔曼滤波在足球机器人定位中的应用[J].装备制造技术,2008(2):45-48.[2]杨洋,罗亚辉,康江,等.基于航迹推算的移动式机器人定位系统设计[J].山西电子技术,2012(2):24-27.[3]THRUNS,FOXD,BURGARDW,etal.Robustmontecarlolocalizationformobilerobots[J].ArtificialIntelligence,2001,128(1/2):99-141.[4]MENEGATTIE,PRETTOA,PAGELLOE.Anewomnidirectionalvisionsensorformonte-carlolocalization[M]∥NARDID,RIEDMILLERM,SAMMUTC,etal.RoboCup2004:RobotSoccerWorldCupVIII.Berlin:Springer-Verlag,2005:97-109.

[5]袁光辉,樊重俊,张惠珍,等.一种新的粒子群算法与人工鱼群算法的混合算法[J].上海理工大学学报,2014,36(3):223-226,238.

[6]刘伟.RoboCup中型组机器人全景视觉系统设计与实现[D].长沙:国防科学技术大学,2004.

[7]卢惠民,刘斐,郑志强.一种新的用于足球机器人的全向视觉系统[J].中国图象图形学报,2007,12(7):1243-1248.

[8]MENEGATTIE,PRETTOA,SCARPAA,etal.Omnidirectionalvisionscanmatchingforrobotlocalizationindynamicenvironments[J].IEEETransactionsonRobotics,2006,22(3):523-535.

[9]YASUDAG,BING.Objectrecognitionandself-localizationforinteractivesoccerrobots[C]∥ProceedingsoftheIEEEInternationalConferenceonRoboticsandBiomimetics.Shenyang:IEEE,2004:407-412.

[10]方正,佟国峰,徐心和.一种鲁棒高效的移动机器人定位方法[J].自动化学报,2007,33(1):48-53.

[11]徐则中,庄燕滨.移动机器人定位方法对比研究[J].系统仿真学报,2009,21(7):1891-1896.

[12]BAISTA,SABLATNIGR,NOVAKG.Line-basedlandmarkrecognitionforself-localizationofsoccerrobots[C]∥ProceedingsoftheIEEESymposiumonEmergingTechnologies.Islamahad:IEEE,2005:132-137.

[13]NEVESAJR,MARTINSDA,PINHOAJ.Ahybridvisionsystemforsoccerrobotsusingradialsearchlines[C]∥Proceedingsofthe8thConferenceonAutonomousRobotSystemsandCompetitions,2008:51-55.

[14]丘柳东,王牛,李祖枢.一种中型自主足球机器人自定位方法[J].计算机工程与应用,2011,47(22):21-25.

[15]LUORH,MINHQ.Anewomni-visionbasedself-localizationmethodforsoccerrobots[C]∥ProceedingsofWRIWorldCongressonSoftwareEngineering.Xiamen:IEEE,2009:126-130.

(编辑:石瑛)

Self-localization Approach for Soccer Robot Based on Self-adaptive Searching

PENG Weiwei1,ZHAO Fengyu2

(1.SchoolofMedicalInstrumentandFoodEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China; 2.SchoolofOptical-ElectricalandComputerEngineering,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

Abstract：In order to solve the problem of robot self-localization in structure environment,a fast and robust approach for self-localization implemented in robotic soccer was presented.In the approach,the probability of robot localization problem was converted to a minimum value in the range of a limited searching space.To achieve high searching efficiency and avoid the local optimum of particle filter method,a self-adaptive search algorithm was provided.The experiment results show that the localization method proposed has the advantages of real time and precision and is superior to other current robot localization methods.

Keywords：self-localization; omni-directional mobilerobot; omni-directional vision; extended Kalman filter; adaptive search

文章编号：1007-6735(2016)03-0281-06

DOI：10.13255/j.cnki.jusst.2016.03.012

收稿日期：2015-01-26

基金项目：国家自然科学基金资助项目(61202376)

通信作者：赵逢禹(1963-),男,教授.研究方向:人工智能、软件工程、智能信息处理.E-mail:zhaofengyv@usst.edu.cn

中图分类号：TP 181

文献标志码：A

第一作者： 彭为微(1981-),女,硕士研究生.研究方向:人工智能.E-mail:pengww314@163.com