一些拉普拉斯谱确定的图

王玉洁,　何常香

(上海理工大学 理学院,上海　200093)



一些拉普拉斯谱确定的图

王玉洁,何常香

(上海理工大学 理学院,上海200093)

摘要：如果与图G同拉普拉斯谱的图都与图G同构,则称图G由它的拉普拉斯谱确定.给出了三类基图为B(P3,P3,P3)(即连接2点的3条长为2的内不交的路)的连通二部双圈图类H(n;n1),H(n;n1,n2)和B(n;n1,n2).证明了H(n;n1),H(n;n1,n2)和B(n;n1,n2)是拉普拉斯谱确定的,且与完全图经并接运算后所得图也是拉普拉斯谱确定的.

关键词：二部双圈图; 拉普拉斯矩阵; 拉普拉斯谱确定

1问题的提出

所考虑的图都是简单连通无向图.n阶连通图G=(V,E)称为双圈图,若G中恰含n+1条边.用A(G)=(aij)表示图G的邻接矩阵,其中,若vivj∈E(G),则aij=1;若vivj∉E(G),则aij=0.用D(G)=diag(d1,d2,…,dn)表示图G的顶点度对角矩阵.矩阵L(G)=D(G)-A(G)为图G的拉普拉斯矩阵,L(G)的特征多项式定义为G的拉普拉斯特征多项式,记为

令μ1≥μ2≥…≥μn=0是L(G)的所有特征值,这些特征值构成的多重集合称为图G的拉普拉斯谱.如果与图G同拉普拉斯谱的图都与图G同构,则称图G由它的拉普拉斯谱确定,简记为DLS.

“哪些图可由它们的谱确定？”这一问题是在1957年发现第一对同谱图后提出的[1].关于同谱图的研究是图谱理论中一个有趣且困难的问题.1966年,Fisher在考虑Kac[2]提出的“一个人能否听到鼓声的形状”的问题时,研究的正是图的谱确定问题.文献[3]提到恰有n个点的图,不能由谱确定的图比能由谱确定的图多.在这个结果出现以后,研究图的谱确定性问题变得热门起来.之后,人们又开始研究拉普拉斯谱确定的问题.如文献[4]证明了T-型树是拉普拉斯谱确定的,文献[5]证明了双星图由其拉普拉斯谱确定,文献[6-7]分别证明了型图和3-玫瑰图是拉普拉斯谱确定的.文献[8-10]分别证明了棒棒糖图、太阳图和沙漏图是拉普拉斯谱确定的.文献[11]研究了双圈图的无符号拉普拉斯特征多项式系数.文献[12]研究了关于H-联图的拉普拉斯特征值.受这些工作的启发,本文研究了二部双圈图与完全图并接后所得图的拉普拉斯谱确定性.

2基本定义

不含悬挂点的双圈图可以分为B(p,l,q)(其中,l≥0,p≥3,q≥3)和B(Ps,Pm,Pl)(其中,2≤m≤min{s,l})两种.

B(p,l,q)是在圈Cp中的点u和圈Cq中的点v加1条长为l的新路uv1v2…vl-1v得到的图,如图1所示.特别地,当l=0时,B(p,0,q)是由唯一公共点u(或v)的圈CP(或Cq)组成的图.

B(Ps,Pm,Pl)是由点x到点y的3条内点不交的路组成的图.设这3条路分别为:长为s-1的路xv1v2…vs-2y,长为m-1的路xu1u2…um-2y和长为l-1的路xw1w2…wl-2y,如图1所示.

可将双圈图按其基图分为如下两类:

图1　双圈图B(p,l,q)和双圈图B(Ps,Pm,Pl)

3基本引理

现介绍一些证明主要结论时需要用到的引理.本文图G的拉普拉斯特征多项式记为

引理1[13]对于图G,由其拉普拉斯谱可以确定图G的以下参数:

a. 顶点数;

b. 边数;

c. 连通分支数;

d. 顶点度的平方和;

e. 生成树个数.

引理2[13]设图G的顶点集和边集分别为V(G)≠φ和E(G)≠φ,有

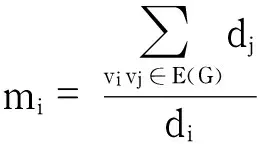
引理3[14]图G的拉普拉斯特征多项式中xk的系数的绝对值

式中:Fk是图G的恰有k个连通分支的生成森林构成的集合;γ(F)为生成森林F∈Fk的各连通分支顶点数的乘积.

引理4[15]设图G是一个恰有n个顶点和m条边的图,(d1,d2,…,dn)为图G的度序列,则在G的拉普拉斯特征多项式中,

式中:τ(G)为图G的生成树数目;nG(C3)为图G中三角形数目.

引理5设(d1,d2,…,dn)和(d′1,d′2,…,d′n)分别为图G和G′的度序列,记

若G与图G′有相同的拉普拉斯谱,则q3(G)=q3(G′).

证明若G与G′拉普拉斯同谱,则l3(G)=l3(G′).由引理1及引理4可知

进一步有

（2）当搅拌机将物料倒放到运料卡车上时，卡车需要前后移动，按前后中的顺序分为三堆，以减少粗集料发生离析的现象。

由生成树的定义,可得引理6.

引理6设图G是双圈图,τ(G)是G的生成树数目.

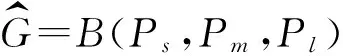
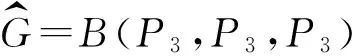
图2　双圈图B(P3,P3,P3)和双圈图B(3,l,4)

证明若图G和G′同拉普拉斯谱,则G′也连通,且G′的边数与G的边数相同,故G′也是双圈图.由引理6可知,τ(G)=12,故τ(G′)=12.

若τ(G′)=12,分两种情况讨论.

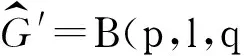
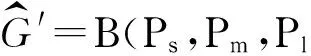
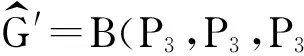
引理8[16]设图G是恰有n个点、m条边的连通DLS图,如果图G同时满足以下3个条件:

b. 图G的边连通度为1;

c.n-m+1≤n-5,即m≥6.

则图G与完全图Kr(其中r为任意整数)并接后所得图G∨Kr也为DLS图.

4图H(n;n1)∨Kr是DLS图

研究二部双圈图H(n;n1)(图3)与完全图Kr并接后所得图H(n;n1)∨Kr(其中r为任意非负整数)的拉普拉斯谱确定性,为了证明这个结论,先证明引理9.

图3　双圈图H(n;n1)

引理9二部双圈图H(n;n1)是DLS图.

证明令G=H(n;n1),设G′是与G拉普拉斯同谱的图.并设G′度为i的点恰有x′i个,i=1,2,…,Δ,其中,Δ为G′的最大度.由引理2

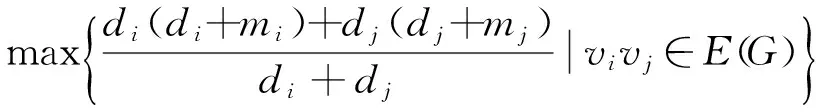
可知

从而有

解得x′1=1,x′2=n-3,x′3=1,x′4=1,故图G′的度序列为(11,2n-3,31,41),因此,图G′与图H(n;n1)同构.

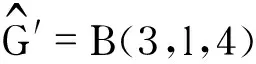
从而有

解得x′1=0,x′2=n,x′3=-2,x′4=2,显然这是不可能的.

综上所述,H(n;n1)是DLS图.

定理1当n≥6,r为任意非负整数时,H(n;n1)∨Kr是DLS图.

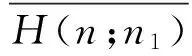
5图H(n;n1,n2)∨Kr是DLS图

研究二部双圈图H(n;n1,n2)(图4)与完全图Kr并接后所得图H(n;n1,n2)∨Kr(其中r为任意非负整数)的拉普拉斯谱确定性,为了证明这个结论,先证明引理10和引理11.

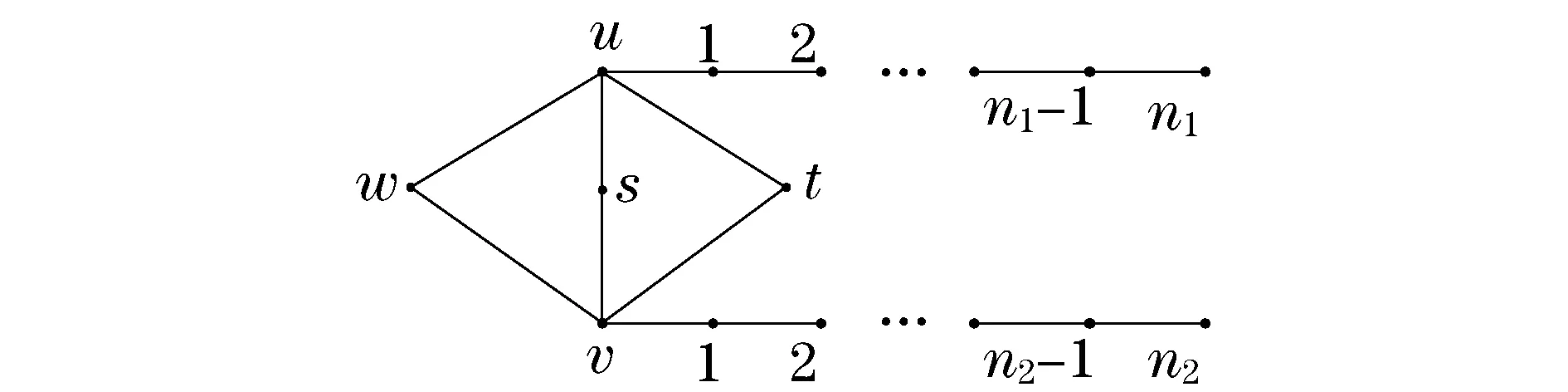
图4　双圈图H(n;n1,n2)

引理102个形如H(n;n1,n2)的二部双圈图,如果具有相同的拉普拉斯谱,则它们必定同构.

若F∈F22,分以下两种情况讨论.

情形1u或v不在F的同一分支中.

此时,γ(F)=(1+n1)(4+n2)或γ(F)=(4+n1)(1+n2)

这样的生成森林共有2个,上述每种情况各1个.

子情形1.2u(或v)只与{w,s,t}中的1个点在F的同一分支中.

此时,γ(F)=(2+n1)(3+n2)或γ(F)=(3+n1)(2+n2)

这样的生成森林共有6个,上述每种情况各3个.

情形2u和v在F的同一分支中,即u与v同时和{w,s,t}中的2个点在F的同一分支中.

此时,γ(F)=1×(4+n1+n2).不难看出,这样的生成森林共有12个.所以

(1+n2)+3×(2+n1)(3+n2)+

3×(3+n1)(2+n2)+12×(4+n1+n2)

综上

n2)2+60(n1+n2)-40n1n2+92

同理

由于n1+n2=n′1+n′2,故有n1n2=n′1n′2,从而有n1=n′1,n2=n′2或n1=n′2,n2=n′1

无论哪一种情况,G与G′均同构.

引理11二部双圈图H(n;n1,n2)是DLS图.

证明令图G=H(n;n1,n2),设G′是与G拉普拉斯同谱的图.并设G′度为i的点恰有x′i个,i=1,2,…,Δ,其中,Δ为G′的最大度.由引理2

可知

所以,Δ≤5.由引理7可知

或

从而有

解得x′1=2,x′2=n-4,x′3=0,x′4=2,x′5=0,故图G′的度序列为(12,2n-4,42),因此,图G′与图H(n;n1,n2)同构.

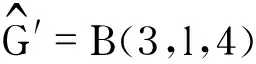
从而有

解得x′1=1,x′2=n-1,x′3=-3,x′4=3,x′5=0,显然这是不可能的.

综上所述,H(n;n1,n2)是DLS图.

定理2当n≥6,r为任意非负整数时,H(n;n1,n2)∨Kr是DLS图.

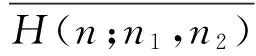
6图B(n;n1,n2)∨Kr是DLS图

研究二部双圈图B(n;n1,n2)(图5)与完全图Kr并接后所得图B(n;n1,n2)∨Kr(其中r为任意非负整数)的拉普拉斯谱确定性,为了证明这个结论,先证明引理12和引理13.

引理122个形如B(n;n1,n2)的二部双圈图,如果具有相同的拉普拉斯谱,则它们必定同构.

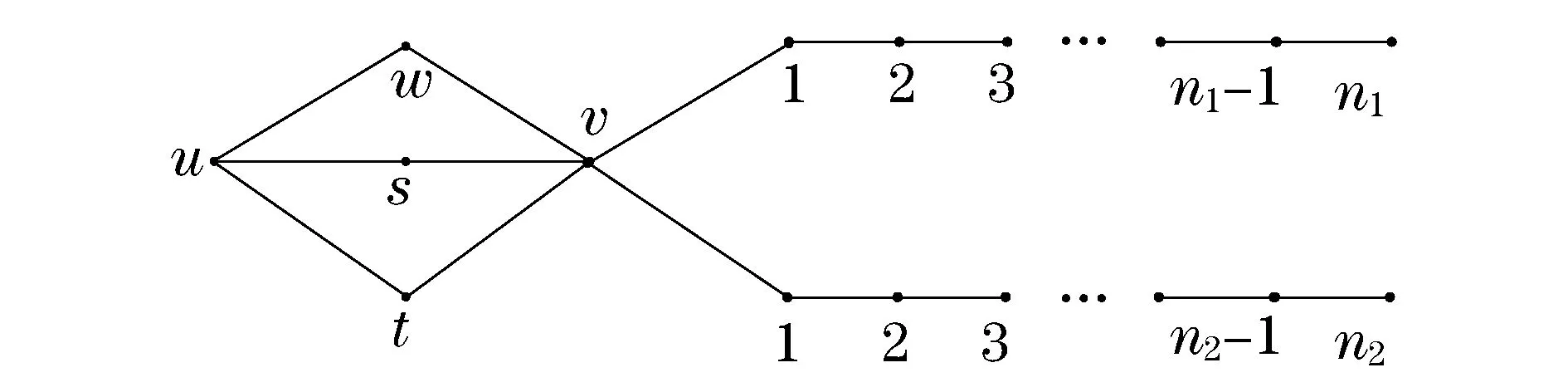
图5　双圈图B(n;n1,n2)

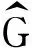
若F∈F22,分以下两种情况讨论.

情形1u或v不在F的同一分支中.

此时,γ(F)=1×(4+n1+n2)或γ(F)=4×(1+n1+n2)

这样的生成森林共有2个,上述每种情况各1个.

子情形1.2u或v只与{w,s,t}中的1个点在F的同一分支中.

此时,γ(F)=2×(3+n1+n2)或γ(F)=3×(2+n1+n2)

这样的生成森林共有6个,上述每种情况各3个.

情形2u和v在F的同一分支中,即u与v同时和{w,s,t}中的2个点在F的同一分支中.

此时,γ(F)=1×(4+n1+n2).不难看出,这样的生成森林共有12个.所以

综上

n2)2+60(n1+n2)-48n1n2+92

同理

由于n1+n2=n′1+n′2,故有n1n2=n′1n′2,从而有n1=n′1,n2=n′2或n1=n′2,n2=n′1

无论哪一种情况,G与G′均同构.

引理13二部双圈图B(n;n1,n2)是DLS图.

证明令图G=B(n;n1,n2),设G′是与G拉普拉斯同谱的图.并设G′度为i的点恰有x′i个,i=1,2,…,Δ,其中,Δ为G′的最大度.由引理2

可知

所以,Δ≤5.由引理7可知

或

从而有

解得x′1=2,x′2=n-4,x′3=1,x′4=0,x′5=1,故图G′的度序列为(12,2n-4,31,51),因此,图G′与图B(n;n1,n2)同构.

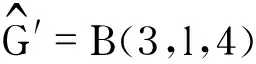
从而有

解得x′1=1,x′2=n-1,x′3=-2,x′4=1,x′5=1;或x′1=0,x′2=n+3,x′3=-8,x′4=5,x′5=0.显然这都是不可能的.

综上所述,B(n;n1,n2)是DLS图.

定理3当n≥6,r为任意非负整数时,B(n;n1,n2)∨Kr是DLS图.

参考文献：

[1]VON COLLATZ L,SINOGOWITZ U.Spektren endlicher grafen[J].Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,1957,21(1):63-77.

[2]KAC M.Can one hear the shape of a drum[J].The Americam Mathmatical Monthly,1966,73(4):1-23.

[3]VAN DAM E R,HAEMERS W H.Which graphs are determined by their spectrum?[J].Linear Algebra and its Applications,2003,373(1):241-272.

[4]WANG W,XU C X.On the spectral characterization of T-shape trees[J].Linear Algebra and its Applications,2006,414(2/3):492-501.

[5]LIU X G,ZHANG Y P,LU P L.One special double star like graph is determined by its Laplacian spectrum[J].Applied Mathematics Letters,2009,22(4):435-438.[6]WANG J F,HUANG Q X,BELARDO F,et al.On the spectral characterizations of-graph[J].Discrete Mathematics,2010,310(13/14):1854-1855.[7]LIU F J,HUANG Q X.Laplacian spectral characterization of 3-rose graphs[J].Linear Algebra and its Applications,2013,439(10):2914-2920.

[8]HAEMERS W H,LIU X G,ZHANG Y P.Spectral characterizations of lollipop graphs[J].Linear Algebra and its Applications,2008,428(11/12):2415-2423.

[9]BOULET R.Spectral characterizations of sun graphs and broken sun graphs[J].Discrete Mathematics and Theoretical Computer Science,2009,11(2):149-160.

[10]LU P L,LIU X G,YUAN Z T,et al.Spectral characterizations of sandglass graphs[J].Applied Mathematics Letters,2009,22(8):1225-1230.[11]徐丽珍,何常香.双圈图的无符号拉普拉斯特征多项式的系数[J].上海理工大学学报,2014,36 (1):12-14.

[12]娄源源,吴宝丰.关于H-联图的拉普拉斯特征值[J].上海理工大学学报,2015,37(2):130-135.

[13]LI J S,ZHANG X D.On the Laplacian eigenvalues of a graph[J].Linear Algebra and its Applications,1998,285(1/2/3):305-307.

[15]KELMANS A K,CHELNOLOV V M.A certain polynomial of a graph and graphs with an extremal number of trees[J].Journal Combinatorial Theory,Series B,1974,16(3):197-214.

[16]ZHOU J,BU C J.Laplacian spectral characterization of some graphs obtained by product operation[J].Discrete Mathematics,2012,312(10):1591-1595.

(编辑:石瑛)

Some Graphs Determined by Their Laplacian Spectrum

WANG Yujie,HE Changxiang

(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：A graph is said to be determined by its Laplacian spectrum,if there is no other non-isomorphic graph with the same Laplacian spectrum.Three types of bicyclic bipartite graphs H(n;n1),H(n;n1,n2) and B(n;n1,n2),which all have the base of B(P3,P3,P3) (three disjoint paths of length 2 between two vertices) were studlied.It is proved that the graphs are determined by their Laplacian spectrum,and the graphs obtained by the join of complete graphs and the above three type bicyclic graphs are also determined by their Laplacian spectrum.

Keywords：bipartite bicyclic graph; Laplacian matrix; determination by the Laplacian spectrum

文章编号：1007-6735(2016)03-0223-07

DOI：10.13255/j.cnki.jusst.2016.03.004

收稿日期：2015-12-30

基金项目：国家自然科学基金资助项目(11201303);上海市自然科学基金资助项目(12ZR1420300)

通信作者：何常香(1979-),女,副教授.研究方向:组合数学与图论.E-mail:changxianghe@hotmail.com

中图分类号：O 157.5

文献标志码：A

第一作者： 王玉洁(1991-),女,硕士研究生.研究方向:组合数学与图论.E-mail:569971787@qq.com