具超线性增长非线性项的拟线性椭圆型方程共振问题

黄　晨,　贾　高,　黄利娜

(上海理工大学 理学院,上海　200093)



具超线性增长非线性项的拟线性椭圆型方程共振问题

黄晨,贾高,黄利娜

(上海理工大学 理学院,上海200093)

摘要：在非线性项具有超线性增长条件下,研究了拟线性椭圆型方程的共振问题.通过建立拟线性算子与线性算子的一种关系,依据Shapiro在加权Sobolev空间中建立的紧嵌入定理和推广的Brouwer定理,运用截断方法证明了近似方程的解存在;借助Sobolev理论、Fatou引理和Lebesgue控制收敛定理证明了上述近似解一致有界;利用投影技巧和Galerkin方法得到共振问题的非平凡解的存在性.

关键词：加权Sobolev空间; 拟线性椭圆型方程; 超线性增长

1问题的提出

在现实生活中,共振现象是常见的.在工程技术中,人们利用或者试图避免共振现象的发生.关于椭圆型方程共振问题有较多的研究,并取得了一系列重要成果[1-8].

1981年Berestycki等[1]用强极大值原理讨论了Dirichlet问题

弱解的存在性.其中，Δ是Laplacian算子，λ1是Laplacian算子的第一特征值，u-是函数u的负部.

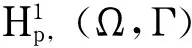
弱解的存在性,T是线性算子.

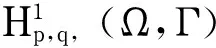
(1)

非平凡解的存在性.其中,算子

非线性项f(x,u)具有超线性增长.

本文所讨论的理论模型来源于研究飞机、汽车、电站的设计和建造，以及环境污染分析等实际背景[3,5].

2假设与引理

设Ω是RN中的有界区域,设Γ⊂∂Ω是一个闭集(可能为空集),pi(x),q(x),ρ(x)∈C0(Ω)是权函数,其中,q(x)是非负的,记p(x)=(p1(x),p2(x),…,pN(x))为向量函数.

考虑准希尔伯特空间

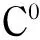
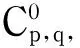
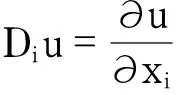
(3)

记

(4)

线性算子

拟线性算子M的二形式分别为

定义1如果满足下面的条件a-e,称区域Ω和算子L满足Simple-VL条件.

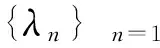
且在Ω上,φ1>0;

c.Ω=Ω1×Ω2×…×ΩN,其中,Ωi⊂R,i=1,2,…,N,是开区域;

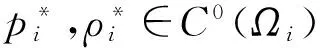
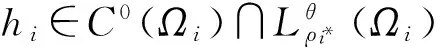
其中

满足以上5个条件的区域和算子的例子有很多,见文献[9-10].

对于算子M和算子L中的aij(x),a0(x),bij(x),b0(x)(i,j=1,2,…,N)作如下假设:aij(x),a0(x)满足条件f-h (bij(x)和b0(x)也满足类似的条件):

f.a0(x),aij(x)∈C0(Ω)∩L(Ω),aij(x)=aji(x),∀x∈Ω,i,j=1,2,…,N;

g.a0(x)≥β0>0,∀x∈Ω;

h. 存在常数c0,c1>0,使得对所有x∈Ω,ξ∈RN,有

对于算子M中的σi(u),假设满足条件i,j:

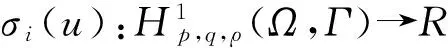
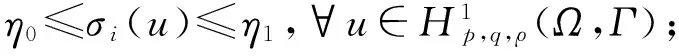
假设问题(1)中的非线性项f(x,s)满足条件k-m:

k.f(x,s)满足Caratheodory条件;

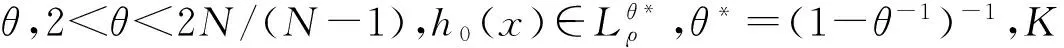
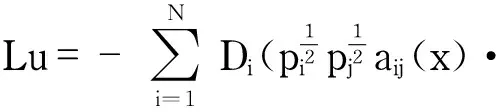
对于加权Sobolev空间,Shapiro在文献[10]中给出并证明了嵌入定理(引理1).

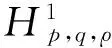
3主要结果及证明

本文的主要结论如定理1.

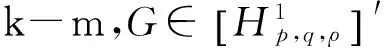
(7)

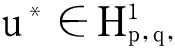
为了证明主要结果,先证明命题1和命题2.

命题1假设定理1的条件都成立,则当n≥2时,存在un∈Sn使得

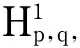
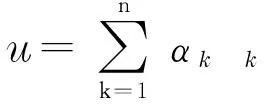
且

(9)

利用定义1的条件f-h,得到

(10)

其中,l=min{c0,β0,1}>0.结合式(9)和式(10),可得

(11)

对于任意正整数m≥2,定义辅助函数

(12)

根据定义1的条件l可知

式中,Tm为与m有关的正常数.

现分两部分证明.

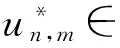
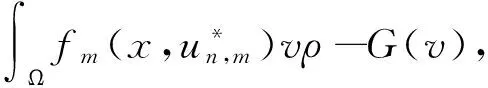
(14)

设

那么,有

其中

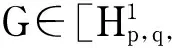
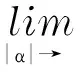
对于式(16),利用式(8)得到

(17)

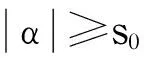
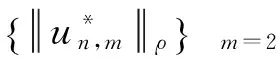
采用反证法.不失一般性,假设

(18)

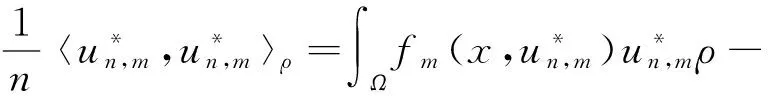
(19)

即

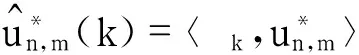
另一方面,对于任意s≥m,由定义1的条件m可得

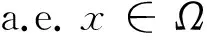
(21)

类似地,当-m≤s≤m和s≤-m时,可以得到同样的结论.因此

根据式(20)和式(22)可以得到

(23)

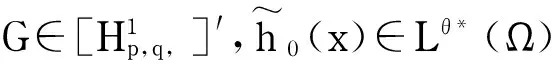
(24)

(25)

因此，由式(25)可得

(26)

运用引理1,有

(27)

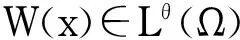
由Hölder不等式,定义1的条件i,m和Lebesgue控制收敛定理,有

将式(14)中的m替换为mj,并且令j→,两边取极限可得式(7)成立.

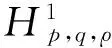
(28)

由于

利用定义1的条件m,通过计算可得

G(un)+L(un,un)-M(un,un)

(30)

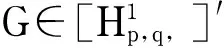
另一方面,根据定义1的条件b,可以找到常数η>0，使得ηλk≤λk-λ1,∀k≥2.

这样,利用引理1,存在常数K2,使得

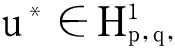
(32)

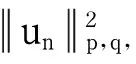
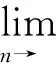
(33)

运用引理1,由式(32)和式(33)可得

(34)

再由式(28)以及算子M和算子L是Near-相关的,可得

(35)

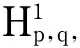
结合式(34)可得

注意到

所以,存在正的常数K4,使得

(36)

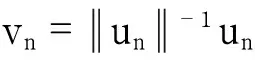
(37)

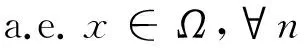
(38)

(39)

(40)

(41)

(42)

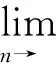
(43)

利用式(34)还可以得到

(44)

(45)

由定义1的条件b可知:任意的x∈Ω,有φ1>0.利用式(28),(36),(39)可得

再利用式(35)和式(36),对于给定的ε>0,存在正的常数n0,当n≥n0时,有

(46)

由定义1的条件m和式(38)得

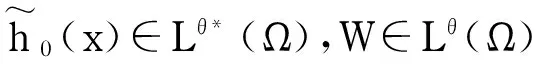
(47)

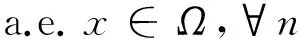
(48)

(49)

(50)

(51)

(52)

设vJ∈SJ,其中,J≥2为任意确定的正整数.那么,对于n≥J,有

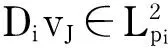
(54)

此外,利用定义1的条件k,l,式(48)和式(49),Hölder不等式和Lebesgue控制收敛定理,可以得到

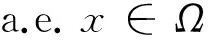
(55)

再由式(47),有

(56)

对式(56)两边取极限n→,根据式(51),(54),(55),有

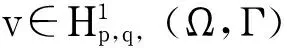
(58)

将式(55)中的vJ替换为PJv,并在等式两边取极限J→,从式(56)得到

因此,定理1成立.

参考文献：

[1]BERESTYCKI H,DE FIGUEIREDO D G.Double resonance in semilinear elliptic problems[J].Communications in Partial Differential Equations,1981,6(1):91-120.

[2]SHAPIROVL.Quasilinearitybelowthe1steigenvalue[J].ProceedingsoftheAmericanMathematicalSociety,2001,129(7):1955-1962.

[3]RUMBOSAJ,SHAPIROVL.JumpingnonlinearitiesandweightedSobolevspaces[J].JournalofDifferentialEquations,2005,214(2):326-357.

[4]RUMBOSA.Asemilinearellipticboundaryvalueproblematresonancewherethenonlinearitymaygrowlinearly[J].NonlinearAnalysis:Theory,Methods&Applications,1991,16(12):1159-1168.[5]LEFTONLE,SHAPIROVL.Resonanceandquasilinearparabolicpartialdifferentialequations[J].JournalofDifferentialEquations,1993,101(1):148-177.

[6]SHAPIROVL.Resonance,distributionsandsemilinearellipticpartialdifferentialequations[J].NonlinearAnalysis:Theory,Methods&Applications,1984,8(8):857-871.

[7]赵美玲,贾高.加权Sobolev空间中奇异拟线性椭圆方程共振问题[J].上海理工大学学报,2012,34(6):598-603.

[8]JIAG,SUND.Existenceofsolutionsforaclassofsingularquasilinearellipticresonanceproblems[J].NonlinearAnalysis:Theory,Methods&Applications,2011,74(10):3055-3064.[9]SHAPIROVL.Specialfunctionsandsingularquasilinearpartialdifferentialequations[J].SIAMJournalonMathematicalAnalysis,1991,22(5):1411-1429.

[10]SHAPIROVL.Singularquasilinearityandhighereigenvalues[M].RhodeIsland:AmericanMathematicalSociety,2001.

[11]KESAVANS.Topicsinfunctionalanalysisandapplications[M].NewYork:JohnWiley&Sons,1989.

(编辑:石瑛)

Resonance Problem of a Quasilinear Elliptic Quation with Superlinear Nonlinearities

HUANG Chen,JIA Gao,HUANG Lina

(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：The resonance problem of a quasilinear elliptic equation with superlinear nonlinearities were focused.By establishing the relationship between the quasilinear operators and linear operators,according to the Shapiro-type compact embedding theorem and Brouwer’s theorem,the existence of solutions of the approximate equation was revealed.With the help of the Sobolev theory,Fatou’s Lemma and Lebesgue dominated convergence theorem,the uniform boundness of the approximate solutions was proved.By using the projection technique and the Galerkin method,the existence of nontrivial solutions of the resonance problem was revealed.

Keywords：weighted Sobolev space; quasilinear elliptic equation; superlinear growth

文章编号：1007-6735(2016)03-0205-06

DOI：10.13255/j.cnki.jusst.2016.03.001

收稿日期：2015-05-17

基金项目：国家自然科学基金资助项目(11171220);沪江基金资助项目(B14005)

通信作者：贾高(1960-),男,教授.研究方向:非线性分析及其应用.E-mail:gaojia89@163.com

中图分类号：O 175

文献标志码：A

第一作者： 黄晨(1991-),男,硕士研究生.研究方向:非线性分析及其应用.E-mail:1285612283@qq.com