基于层次分析法的供应商风险评估指标

胡 爽 董周战

（中国空空导弹研究院，河南 洛阳 471000）



基于层次分析法的供应商风险评估指标

胡 爽 董周战

（中国空空导弹研究院，河南 洛阳 471000）

[摘要]结合企业实际供应商管理状况，运用层次分析法构建了供应商风险评价模型，并对供应商的供货风险进行了分析和评价。

[关键词]供应商风险；层次分析法；指标体系；分析及评价

[收修订稿日期] 2016-01-24

基于未来联合作战模式，航空装备产品利益攸关方的需求和要求急剧增加，航空装备产品及其与使用环境的交联关系不断增加，系统及其与子系统设计、综合的复杂度和风险不断提高，产品技术创新性和管理复杂度越来越高，必须依靠国内相关技术专业内知名企业组成联合研制团队开发产品，外包成为复杂系统研制中的重要一环；供应商协同研发模式体现出供应商的贡献度越来越大，供应商管理地位日趋凸显，如何降低和避免供应商风险带来的损失，已成为企业赢得市场和获取竞争优势的重要战略之一。本文从企业的视角出发，结合层次分析法研究成果的运用，对某航空企业供应商进行风险评估。

1　供应商风险评价常用方法

供应商风险评价方法研究大致经历了定性、定量、定性与定量相结合3个阶段。早期的供应商风险评价方法采用定性方法，主要是根据经验进行主观的判断，这种方法由于缺少科学依据而较少采纳。定量的方法主要包括成本法、线性规划法、非线性规划法、模糊规划、多目标规划、数据包络分析、各种智能方法和实践方法。目前研究比较多的供应商风险评价模型主要有数学规划模型、人工智能技术，以及线性权重模型。这3种方法都存在局限性，数学规划模型的优势是定量分析，但复杂和繁琐的数据使其失去现实可操作性。人工智能技术基于案例推理和神经网络的方法过度依赖稀缺的案例数据。线性权重模型中层次分析法使用较多，它通过构建判断矩阵将复杂的问题条理化、层次化，因此，与其他方法相比，层次分析法用于供应商风险评估较为合适。

2　层次分析法基本原理

层次分析法（Analytic Hierarchy Process，AHP）是由美国运筹学家、匹兹堡大学萨蒂（T. L.Saaty）教授提出的一种定量与定性相结合，将问题分解成不同的组成要素，将要素按不同层次组合，进行综合分析的决策方法。

层次分析法在供应商风险评价中应用的基本步骤如下。

2.1建立递阶层次结构

递阶的层次决策结构模型如图1。

2.2运用二二比较法，构造成判断矩阵

Satty教授提出用1～9尺度，构成判断矩阵，并得出权重。萨蒂标度法如表1。

同一层第i个元素与第j个元素相对于上一层某个因素的重要性时，使用数量化的相对权重aij来描述，设共有n个元素参与比较，构造出判断矩阵：A= (aij)n×n，矩阵中元素由专家根据实际经验按表1的定义来评定尺度数量值。其中：aij＞0，aij=1/aji，aii=1(i、j=1，2，3，…，n)。

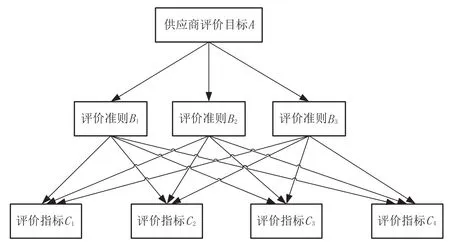
图1　供应商风险评价层次结构图

表1　萨蒂标度

2.3确定要素权重及一致性检验

根据判断矩阵中元素间相互比较，利用求和法，将判断矩阵A按列归一化，再将归一化的矩阵按行求和，继续归一化，即可得到A的特征向量：W=（w1、w2、… wn）T，特征向量就是各指标的权重。权重是对评价指标定性判断的量化，实际操作中可由设计、工艺、质量、物资、生产等成员组成的评价小组共同参与完成。

为了保证在对元素进行比较时没有自相矛盾的结论，对权重向量进行一致性检验，以验证判断矩阵是否满足一致性。

一致性检验公式：C.I.=（λmax-n）/（n-1），其中 λmax=1 / n • ∑ ［（A • Wi）/ Wi]

当C.I.=0时，A为一致阵；C.I.越大，A的不一致程度越严重，C.I.越小，说明一致性越好。

为更好评价一致性，Satty教授又提出平均随机一致性指标 R.I.（是足够多个随机发生的判断矩阵计算的一致性指标的平均值）。

1～10阶矩阵的R.I.值见表2（表2中数值为500个样本平均值）。

如比值C.I. / R.I.小于0.1，就认为判断矩阵具有较高的一致性。

层次数的多少取决于系统分析的需要。最高层元素只能有1个，每一个元素所支配的下一层元素一般不超过9个，元素过多时可进一步再分组。同一层内及不同层次的各元素相互独立，不存在包含关系。

3　建立供应商风险评估指标体系

为使供应商风险评价更客观全面，企业通过组织或聘请专家团队，运用风险评价小组头脑风暴，确定企业供应商风险评价因素，按照层次分析法要求，将评价系统层层分解，最终建立风险评价指标体系，如图2。

表2　多阶比较矩阵的平均一致性指标数值表

评价目标共分为3个层次：由高到低分别为目标层、准则层、指标层，Wi表示各层元素对上一层的相应权重。

第一层（目标层A）：供应商风险评价目标A；

第二层（准则层B）：质量风险B1，进度风险B2，成本风险B3；

第三层（指标层C）：准则层相对应的评价项目C1、C2、C3。

4　应用实例

以某航空企业供应商风险管理为例来验证。从供应商质量、进度、成本3个指标两两比较，构成矩阵如下，通过每列向量归一化，并按行求和，所得W即为供应商质量、进度、成本3个指标的权重。

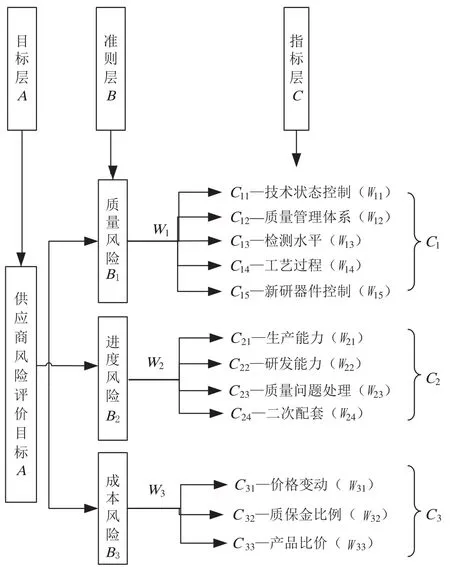
图2　供应商综合评价指标体系

C.I.=0.003 7；C.I./ R.I.=0.006 4＜0.1，满足一致性要求，说明矩阵可以接受。同理可求出指标层C各因素的权重。由此，可算出所有指标对目标层A的综合重要度，如表4。

在实际运行过程中，由于供应商风险评价涉及的因素很多，既有定性因素，也有定量因素，因此，评价小组只有通过综合不同评价者的意见，根据供应商风险评价指标体系及权重，才能得出一个全面、客观的评价。

5　风险分析及评价

5.1建立风险等级

根据某航空企业型号产品特点，将综合风险值P等级按表5标准划分。

5.2建立评判等级

风险发生的可能性等级是对风险发生可能性的度量，根据型号产品情况将发生可能性等级定位5级。建立供应商评判向量5等级划分制，如表6。

表4　供应商风险评估指标权重值

表5　综合风险等级标准

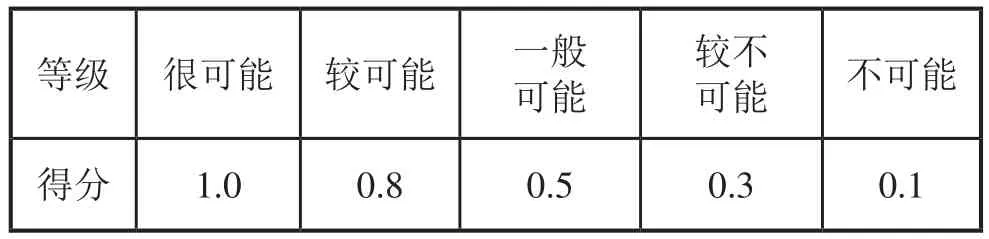
表6　供应商评判向量5等级划分表

5.3确定风险评判值

由企业设计、工艺、质量、物资、生产组成的评价小组成员根据五等级划分表，分别各自对供应商风险评价指标层的各项指标给出风险评判值，如表7。

由表7中的各风险评判值建立起供应商的判断矩阵R，通过公式B = W • R，计算出判断矩阵B，进而计算出目标层向量U，再通过以下公式，最终得出综合风险值P：

P = U｛1.0 0.8 0.5 0.3 0.1｝′= 0.427

根据风险等级，可知该供应商的综合能力风险等级为一般风险。

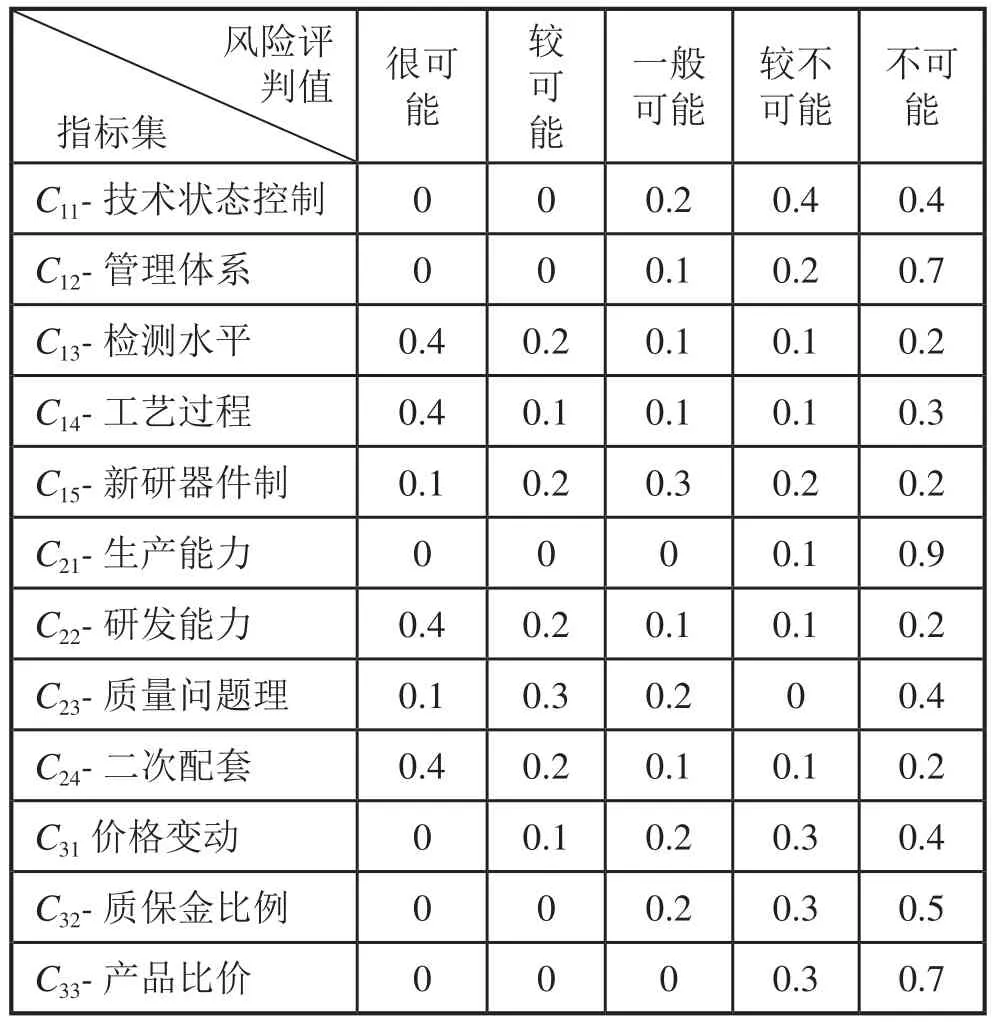
表7　指标给出风险评判值

风险预警机制是降低产品风险损失的有效手段，企业可根据不同的风险等级采取应对措施，控制不良后果发生，使项目得以顺利进行。

6　结束语

本文针对企业供应商管理实际情况，通过运用层次分析法，建立了供应商风险评估指标体系，科学、合理地分配了供应商风险评价各因素的权重，较好地将定性分析与定量分析相结合，并对指标情况进行了分析，证明了该指标体系的有效性。

[参考文献]

[1] 许树伯. 层次分析法原理 [M]. 天津：天津出版社，1988：1-100.

[2] 宋慧刚.层次分析法在管理中的应用 [J]. 中国科技信息，2005（22）.

[3] 朱铎辉，吴志军，张玉峰. 基于层次分析法的供应商评价模型的研究 [J]. 计算机应用研究，2004（6）：90-92.

[4] 邵良杉，杜文涛. 基于模糊逻辑的供应商选择[D]. 辽宁工程技术大学学报，2007(6).

（编辑：劳边）

[中图分类号]F273.2

[文献标识码]C

[文章编号]1003-6660（2016）02-0035-04

[DOI编码]10.13237/j.cnki.asq.2016.02.009