基于径向基神经网络的白矮主序双星自动分类
王文玉,郭格霖,姜 斌,王 丽
山东大学(威海)机电与信息工程学院, 山东 威海 264209
基于径向基神经网络的白矮主序双星自动分类
王文玉,郭格霖,姜 斌,王 丽*
山东大学(威海)机电与信息工程学院, 山东 威海 264209
白矮主序双星的光谱特征是决定其类型的关键因素,如何有效提取恒星光谱的特征是亟待解决的问题。提出一种新的方法,通过构建模型捕获恒星光谱数据的特征,对SDSS-DR10海量光谱进行自动分类。径向基神经网络作为一种有效的计算模型,在数值逼近和目标分类上均有较好的表现效果,但由于目前神经网络超参数的确定大多数依赖于实验经验,很大程度上制约了算法能力的发挥。在分析白矮主序双星光谱数据的高维分布特征的基础上,提出一种基于径向基神经网络的白矮主序双星自动分类模型,并以白矮主序双星的光谱特征为导向,针对恒星光谱提出了中心准则和宽度准则以确定神经网络的超参数,大幅度提高了模型的准确度。实验对分类模型进行数值训练并使用训练的模型对SDSS-DR10光谱数据进行白矮主序双星的自动分类,共发现4 631个白矮主序双星,通过Simbad,NED和Google交叉验证后发现其中有25个是未予以收录的新候选体。实验结果验证了该模型在大规模白矮主序双星自动分类任务中的有效性,新发现的白矮主序双星也为特殊天体的进一步研究补充了有效数据。
白矮主序双星;径向基神经网络;自动分类;中心准则;宽度准则
引 言
位于新墨西哥州阿帕奇山顶天文台的斯隆数字巡天SDSS是有史以来具有重大突破性的巡天项目[1]。随着2015年1月最新观测数据DR12的发布,海量的天体观测数据向特殊天体的自动发现工作发起挑战。在这些海量的天体观测数据中隐藏着很多稀少天体,时变天体以及未知天体。而白矮主序双星(white dwarf-main sequence,WDMS)作为一种特殊的双星系统,对求恒星的半径、质量等参数有着非常重要的作用。对于还没有发生物质交流或者没有在白矮星周围形成吸积盘的WDMS双星系统,可以被近似认为白矮星和M型主序星之间没有或者有很弱的相互作用,因而它们的光谱可以看成是白矮星光谱和M型主序星光谱的简单叠加。
目前,发现WDMS的方式仍以模板匹配、测光筛选以及人工判定的方法为主导。其中司建敏[2]在应用核密度估计与人工判定研究特殊天体的过程中发现了1颗未予以收录的WDMS,任娟娟[3]使用颜色筛选的方式从LAMOST望远镜的先导巡天数据中发现了28颗未被收录的WDMS,Mansergas[4]使用模板匹配的方法从DR7中发现了2 248个WDMS候选体,但是这几种方法都存在需要进行大量人工干预的问题,难以广泛应用到TB级别的海量天体光谱中。
径向基(radial basis function,RBF)神经网络是一种具有数据局部特征捕捉能力的神经网络,和传统的BP神经网络相比,RBF有如下优点:(1)收敛速度快[5];(2)函数结构更加紧凑[6];(3)应用范围广泛[7]。但由于RBF网络的超参数没有统一的确定方式,导致该算法的大规模实施存在一定的难度。
本文结合K-means算法,引入了中心准则和宽度准则,确定了白矮主序双星RBF网络模型,对SDSS的DR10数据进行自动挖掘。
1 WDMS径向基神经网络
径向基神经网络是具有单隐含层的局部神经网络,构造如图1所示的RBF网络系统用于完成WDMS分类任务。虽然RBF网络是一个局部学习器,但Léon Bottou等[8]已发现通过合理地控制网络的超参数,能够利用RBF网络去逼近全局学习器。基于此,图1中的决策信息从WDMS光谱实验中获得:(1)通过交叉检验准确率确定主成分的数量;(2)基于K-means算法和两个准则确定网络的超参数(样本中心和局部宽度)。

图1 预处理与发现WDMS的分类系统
标准RBF网络的隐含层计算单元为高斯函数。对于输入光谱x={x1,x2,…,xn},RBF网络拟合判别函数
(1)
隐含层结点和输出层结点的传递函数采用Sigmoid函数,将网络的输出限制在(0,1)区间内,具体形式为
(2)
网络的输出函数进一步改写为
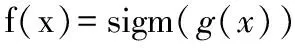
(3)
通过基于梯度下降的优化方法求解输出函数的系数{w1,w2,…,wk}和b0。
1.1 中心准则
大量实验表明,在欧几里得范数的度量下同种类型的天体光谱之间通常具有更近的距离,因此采用K-means算法选择光谱作为样本中心。在针对WDMS光谱的实验中发现,为使模型达到最优的泛化效果,RBF网络所需的隐含层神经元个数满足
(4)
其中n为训练样本总数,c为训练光谱的类别总数,d为输入样本的维度,β∈(0,1]称为宽度约束因子,当光谱的高维分布越分散时,通常希望β的值越大。
1.2 宽度准则
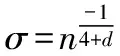
(1)定义中心距离矩阵D,对于矩阵中的元素
(5)
(2)计算最近中心距
(6)
(3)计算每一个类中心拥有的样本点距离类中心的平均距离。即构建距离数组R,其中
(7)
(4)定义神经元对应的宽度
(8)
宽度准则保证模型能对光谱的局部分布特征进行有力捕捉,使隐含层结点根据光谱的分布获得不同程度的激活。
2 实验数据及预处理
本文的实验数据来源于SDSS DR10恒星光谱数据,选用类型确定的12 000条光谱训练RBF模型,之后将模型对DR10中2 462 508条光谱进行深度挖掘。训练数据分布见表1。

表1 样本分配
对每一条光谱进行归一化处理并应用主成分分析法进行降维。为权衡运算时间与模型准确度,通过实验结果(表2)确定最终主成分数量为27。
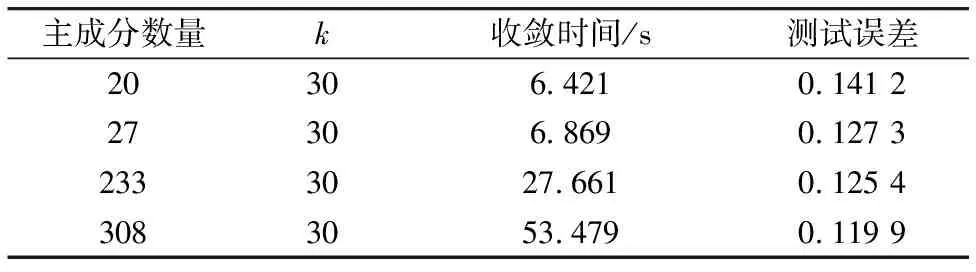
表2 参数性能
表2中k为通过中心准则确定的隐含层结点数量。
3 结果及分析
3.1 K-means有效性验证
本实验采用K-means算法确定隐含层结点的样本中心。相较于随机从样本点中选取光谱作为中心,K-means在表现效果上优于随机方法。见图2。随着隐含层结点的增多,两种算法确定的模型呈现出不同的最优解(K-means:k=30,MSE=0.1;Random:k=102,MSE=0.13)。
如图2所示,应用K-means算法确定的系统(系统1)在分类误差上低于随机算法所确定的系统(系统2),且两者在达到最优解时,系统1所需的隐含层结点远少于系统2,大大降低了系统出现过拟合的风险[10]。
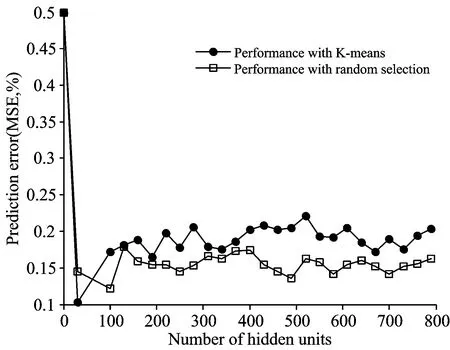
图2 K-means与随机算法确定样本中心比较
3.2 WDMS光谱激活
通过K-means算法确定隐含层结点参数时确定k=30,该过程产生3个WDMS代表结点。对应光谱见图3。由于RBF网络的局部特性,各隐含层结点捕捉到了不同类型光谱的局部特征,表现为赋予不同结点的权值随着迭代次数的增加有着不同的变化趋势。见图4。以WDMS光谱为簇中心的结点在各次迭代中得到最大程度激活,而其他结点则随着迭代次数的增多不断被抑制。
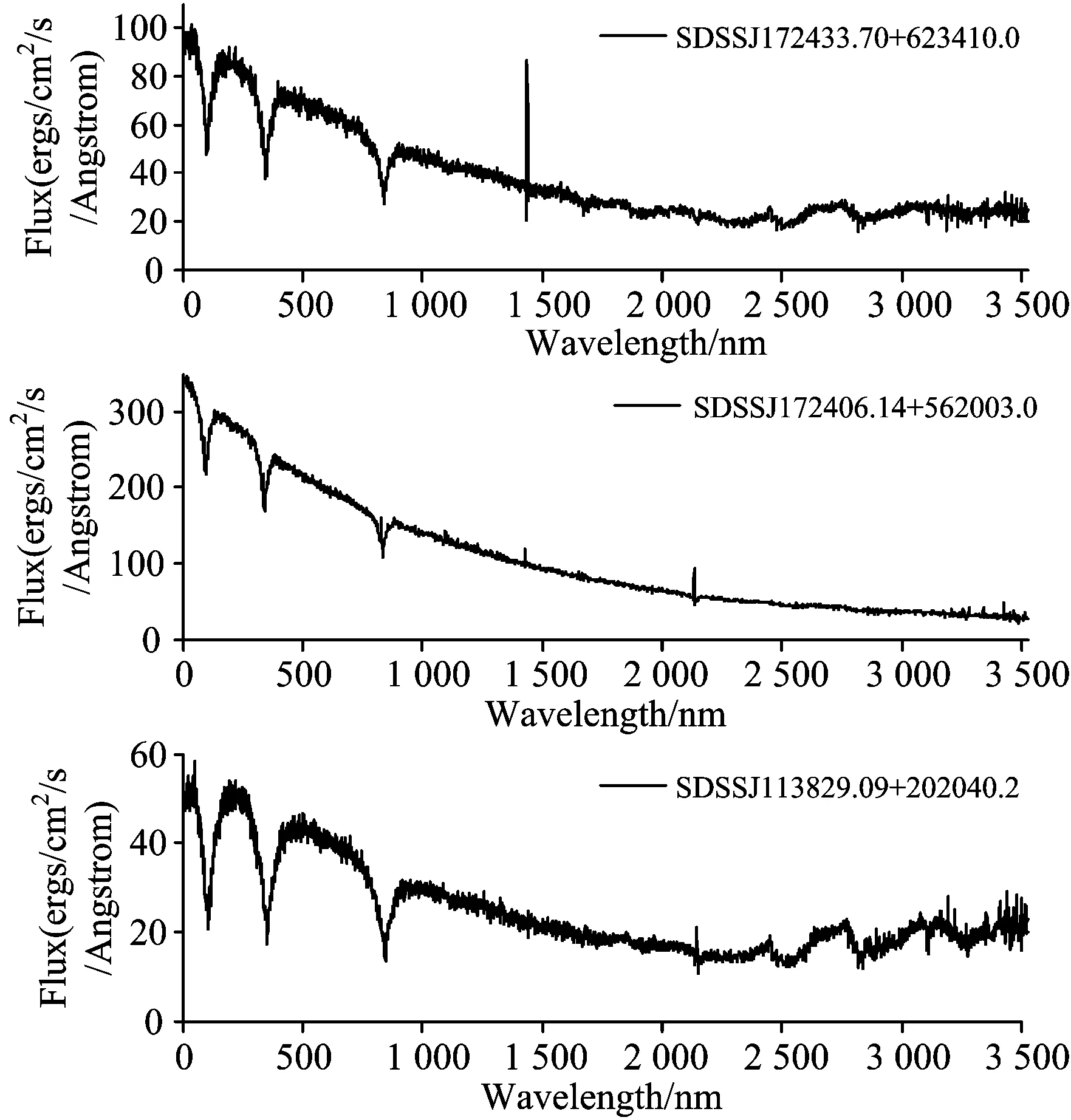
图3 K-means确定的WDMS光谱
训练后的RBF网络对每一条未知类型的输入光谱,输出该光谱是WDMS的概率。
3.3 挖掘结果
本工作最后使用训练后的RBF网络对SDSS DR10中所有光谱进行海量挖掘,共产生4 631条WDMS光谱,经过Simbad,NED和Google检验后确定其中25个是未被收录的新源。新候选体的信息见表3。

图4 WDMS中心点和其他隐藏单元
表3 实验结果
Table 3 Results of experiment
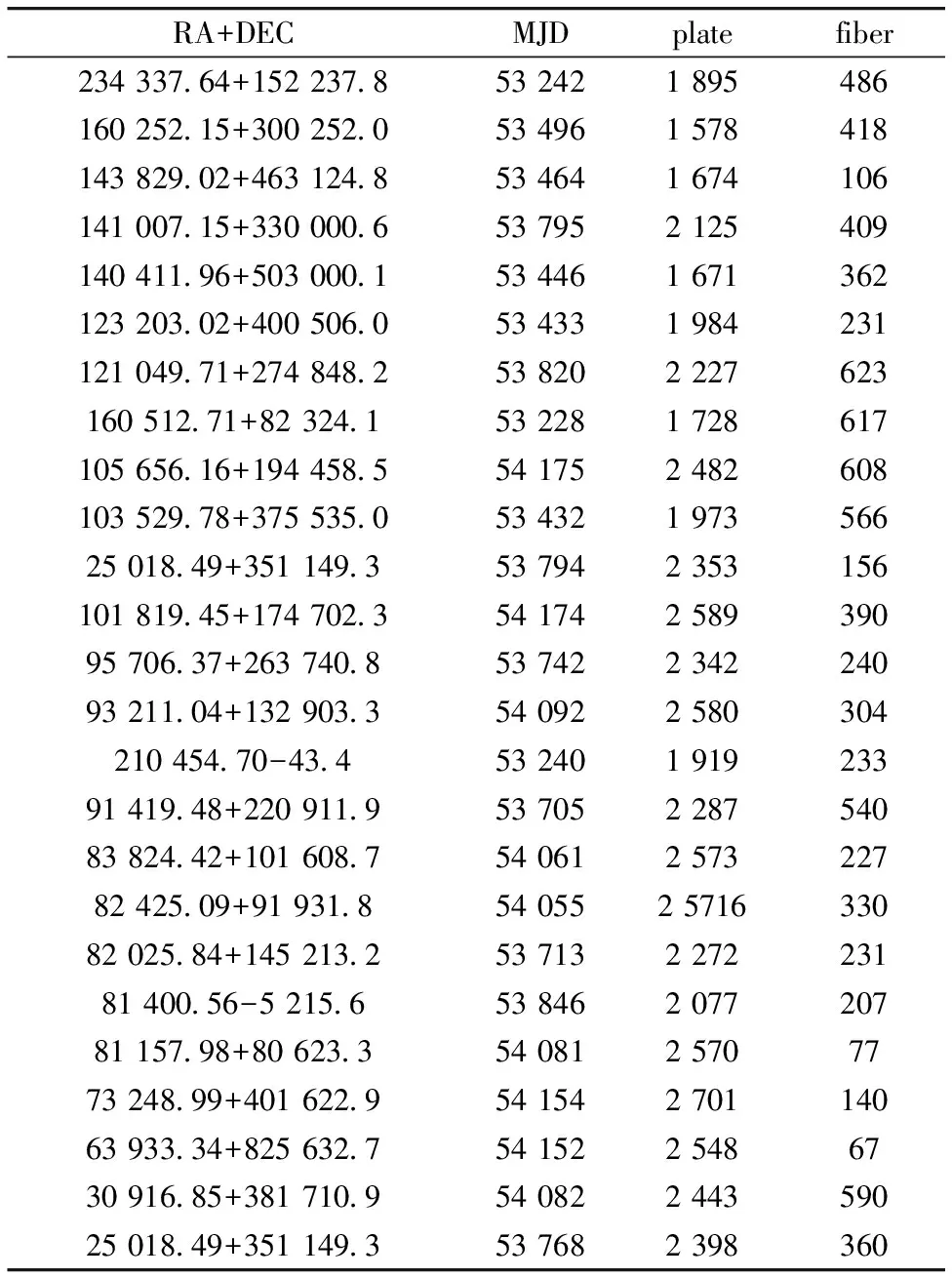
RA+DECMJDplatefiber234337 64+152237 8532421895486160252 15+300252 0534961578418143829 02+463124 8534641674106141007 15+330000 6537952125409140411 96+503000 1534461671362123203 02+400506 0534331984231121049 71+274848 2538202227623160512 71+82324 1532281728617105656 16+194458 5541752482608103529 78+375535 053432197356625018 49+351149 3537942353156101819 45+174702 354174258939095706 37+263740 853742234224093211 04+132903 3540922580304210454 70-43 453240191923391419 48+220911 953705228754083824 42+101608 754061257322782425 09+91931 8540552571633082025 84+145213 253713227223181400 56-5215 653846207720781157 98+80623 35408125707773248 99+401622 954154270114063933 34+825632 75415225486730916 85+381710 954082244359025018 49+351149 3537682398360
4 结 论
通过引入中心准则和宽度准则,提出了RBF网络在恒星光谱数据上超参数(中心参数、局部宽度)的一种确定方式,有效避免了网络超参数仅能依靠经验确定的弊端,为网络的表现能力给予了一个良好的解释。实验证明,将训练好的RBF网络用于大规模WDMS的发现十分有效。
通过对比实验3.1验证了该方法的有效性。在对于WDMS的分类任务上,RBF和传统多层感知机(MLP)相比具有更快的收敛速度和唯一的全局最优解,大幅度提高了WDMS在海量恒星光谱中的分类准确率。
由于深度神经网络的发展,浅层网络(2~3个隐含层)在复杂任务上的表现受到挑战,如何将浅层模型进行深度拓展是今后一个重要的研究趋势。由于大多数恒星光谱的数据具有高维、信噪比低等特点,如何利用伤工智能算法对恒星光谱进行强针对性的预处理也是一个重要的研究方向。
[1] Dawson Kyle S, Schlegel David J, Ahn Christopher P, et al. The Astronomical Journal, 2013, 145(1): 41.
[2] SI Jian-min, LUO A-li, WU Fu-zhao, et al. Spectrosc. Spectr. Anal., 2015, 35(3): 834.
[3] Ren J, Luo A, Li, et al. The Astronomical Journal, 2013, 146(4): 82.
[4] Rebassa-Mansergas A, Nebot Gomez-Moran A, Schreiber M R, et al. Monthly Notices of the Royal Astronomical Society, 2011, 402: 620.
[5] Moody J,Darken C J. Neural Computation, 1989.
[6] Lee S,Kil R M. Neural Networks, 1991.
[7] Park J,Wsandberg J. Neural Computation, 1991.
[8] Bottou E, Vapnik V. Neural Computation, 1992, 4(6): 888.
[9] Härdle W, Müller M, et al. Springer, 2004.
[10] Yuan J L,Fine T L. IEEE Trans. Neural Networks,1998.
(Received May 6, 2015; accepted Sep. 10, 2015)
*Corresponding author
Discovering WDMS with Automatic Classification System Based on RBF Neural Network
WANG Wen-yu, GUO Ge-lin, JIANG Bin, WANG Li*
School of Mechanical, Electrical & Information Engineering, Shandong University, Weihai, Weihai 264209, China
A model which is capable of capturing the spectral distribution features helps to improve the WDMS(White Dwarf + M Sequence Binaries) classification system running in SDSS-DR10 because the distribution feature of a spectra is one of the most important factors that determine its spectral type. Radial basis function (RBF) neural network is an efficient computational model that is widely used for numerical approximation and object classification. However, due to the reason that the network’s hyper-parameters are usually determined empirically, the performance of the network is limited. In this paper, on the basis of analyzing the distribution features of WDMS in a high dimensional space, an automatic classification model for WDMS ia propose based on RBF neural network. And according to the features, we propose centroids criterion and width criterion to determine hyper-parameters for the network in a more theoretical way, which improves the accuracy of the model. After training and applying the model, a total number of 4 631 WDMS candidates are classified and 25 of them are newly identified, which proves the feasibility of the model and provides further researches on WDMS with more data.
WDMS;Radial basis function (RBF) neural network;Automatic classification;Centroids criterion;Width criterion
2015-05-06,
2015-09-10
国家自然科学基金项目(11473019), 山东省自然科学基金项目(ZR2014AM015),山东大学基本科研业务费项目(2015ZZXM002)资助
王文玉,1976年生,山东大学(威海)机电与信息工程学院博士研究生 e-mail: sdwangwenyu@163.com *通讯联系人 e-mail: hochi@sdu.edu.cn
O657.3
A
10.3964/j.issn.1000-0593(2016)10-3360-04
- 光谱学与光谱分析的其它文章
- Gd靶激光等离子体光源离带辐射及其等离子体演化的研究
- Probing the Binding of Torasemide to Pepsin and Trypsin by Spectroscopic and Molecular Docking Methods
- Mn(Ⅱ)-5-Br-PADAP共沉淀-火焰原子吸收光谱法测定虾、贝样中的镉
- Near Infrared Spectroscopy Study on Nitrogen in Shortcut Nitrification and Denitrification Using Principal Component Analysis Combined with BP Neural Networks
- 内蒙古草原植被最大光能利用率取值优化研究
- 健康和糖尿病大鼠红细胞荧光光谱非线性程度差异

