非线性流行降维与近红外光谱分析技术的大米贮藏期快速判别
林 萍,陈永明*,邹志勇
1. 盐城工学院电气工程学院,江苏 盐城 224051
2. 四川农业大学机电学院,四川 雅安 625014
非线性流行降维与近红外光谱分析技术的大米贮藏期快速判别
林 萍1,陈永明1*,邹志勇2
1. 盐城工学院电气工程学院,江苏 盐城 224051
2. 四川农业大学机电学院,四川 雅安 625014

大米;贮藏期;流形降维;近红外光谱技术;核偏最小二乘
引 言
研究表明,稻米收获存放数月后易发生质变,其营养成分往往伴随各种理化反应而大大衰减。贮藏时间较短的新米口感好、营养价值高,具有较高的市场利润,而贮藏时间较长的陈年大米口感较差、营养成分损失较为厉害,市场销量不佳。大米贮藏期限的差别导致大米市场的销售价格上存在巨大差异,因此一些不法商贩将三年以上的陈米经过抛光处理后当作新米出售,从中获取暴利[1]。目前,大米的贮藏期由人工根据其色泽及相关营养成分含量等进行判断,但是陈米经抛光处理后色泽几乎与新米一样,分辨难度大,而采用理化的监测方法鉴别其内部营养成分往往耗时长、操作复杂,难以满足实际应用中快速准确鉴别的需要。因此,寻求一种高效、准确的检测方法对新米和陈年米的鉴别显得尤为重要。
目前,近红外光谱分析技术已经应用于食品质量的检测。肖昕等[2]应用近红外透射光谱技术, 采用不同回归统计分析方法建立精米蛋白质含量(PC)定量回归方程。模型具有较好的预测效果。陈孝敬等提出了一种利用多光谱图像纹理特征进行大米分类的新方法,大米识别率达到了100%。吴迪等[3]利用近红外光谱结合判别偏最小二乘法建立定性模型,实现对不同品牌奶粉内部营养成分的定量测量,正确识别率达100%。李晓丽等[4]通过对近红外光谱数据进行神经网络系统训练,成功地对杨梅品种快速判别预测。张鹏等[5]通过近红外漫反射光谱技术建立了柿子不同品种和贮藏期的快速判别方法,不同贮藏期的正确分类率达到 97.78%。但针对大米贮藏期时间的研究鲜有报道。本研究的目的是利用近红外光谱分析技术结合现代化学计量学方法实现对大米贮藏时间的快速鉴别。
1 实验部分
1.1 仪器设备与数据采集
采用Handheld Field Spec光谱仪(Analytical Spectral Device(ASD),Boulder,USA)获取实验数据,光谱分辨率为2 nm,光源采用14.5 V卤素灯。采集系统原理如图1所示。对实验大米样本采集340~1 075 nm的漫反射光谱,不同贮藏期样本的光谱采集采用交替进行的方式,每个样本光谱扫描次数设定为30次取平均值。实验用新米和三年陈米样本各200个,由四川农业大学水稻生物学实验室提供。随机选取300个大米样本作为建模集, 剩余100个样本作为预测集。数据分析软件采用Matlab R2014a (The Math Works, USA)。
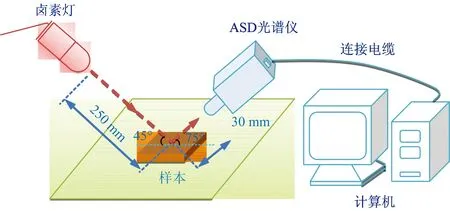
图1 大米样本反射光谱检测系统原理图
1.2 流形降维法
流形降维法是由有限样本点集合来计算嵌入在高维欧式空间中的低维流形的问题,目的是找出隐藏在高维空间中的低维结构,找出数据集分布的隐含规律性[6]。给定数据集X={xi,i=1, …,N}∈RD,并假设x中的样本是由低维空间中的数据集Y={yi,i=1, …,N}∈Rd通过某个非线性变换f所生成,即:xi=f(yi)+εi,其中d≤D,f:Rd→RD是C∞嵌入映射[7]。通过给定的观测数据集X: 获得数据的低维表示形式Y={yi,i=1, …,N}∈Rd;构造高维到低维的非线性映射f-1:RD→Rd。目前,常用的非线性降维方法有等距映射(isometric feature mapping, ISOMAP)[8]、局部线性嵌入(local linear embedding, LLE)[9]、拉普拉斯特征映射(Laplacian eigenmaps, LE)[10-11]等。
1.3 核偏最小二乘法(KPLS)
Rosipal等在偏最小二乘回归(partial least squares, PLS)基础上进一步提出了核偏最小二乘回归法[12], 从而使偏最小二乘回归法能用于解决非线性回归的问题。基于核函数的偏最小二乘方法(kernel partial least squares, KPLS)其原理是将PLS回归分析法与核函数理论相结合,将输入数据矩阵X通过核函数T(X)映射到特征空间中并结合PLS进行运算。这样原空间的非线性关系就与特征空间中的线性PLS相对应,由于核函数是以内积的形式存在,因此在模型建立过程中不需要具体求解核函数的表达式。其中,合理选择核函数是影响模型效果的重要因素,选择合理的核函数可以有效处理好数据间的非线性关系[13]。目前使用较多的核函数包括径向基(radial basis function, RBF)核函数、多项式(polynomial)核函数和线性(linear)核函数。
2 结果与讨论
2.1 光谱曲线分析
测量得到的陈年米与新米可见近红外光谱的反射率曲线如图2所示。图中横坐标为波长,纵坐标为反射率。从图2可以看出,陈年米与新米的光谱曲线的趋势非常相似,基于人工的判别方式难以区分陈年米与新米。另外,特征光谱曲线表现出了一定的非线性特性,因此需要对大米光谱非线性进行定量分析,进而采用相应的非线性算法对大米贮藏期实现定量与定性测量。在对光谱数据进行非线性检测前,原始光谱数据经过直接正交信号矫正(DOSC)处理,去除无关变量以及光谱基线漂移的影响。

图2 不同大米样本可见近红外反射光谱曲线
2.2 非线性性定量分析
采用两种定量的数值统计方法Durbin-Watson测试法[15]和Run测试法[15]来定量分析光谱数据的非线性程度。实验计算得到Durbin-Watsond值为1.732,大于临界值dH=1.40。基于Run测试法的检验值z为3.128,大于临界值1.96,试验数据表明,采集到的大米光谱数据存在显著的非线性结构;图3为增强偏残差图(augmented partial residual plot,APaRP)[16]能够更直观地反映大米光谱数据的非线性度。图3显示了第1主成分与前6个主成分残差多项式拟合的结果,可以看出大米光谱数据集存在显著的非线性。

图3 增强偏残差图检测大米数据的非线性
2.3 流行降维方法比较
图4是分别采用线性流行降维方法PCA (principle components analysis)和MDS (multidimensional scaling)以及非线性流行降维方法ISOMAP,LLE和LE提取的本真变量个数与交叉验证均方根误差(root mean square error for cross validation, RMSECV)关系曲线图。通过比较分析发现,非线性降维得到的本征变量的个数比线性方法多。这是由于一些非线性的特征变量在线性降维过程中无法考虑进去,而非线性降维方法的特点是将所有输入变量映射到高维空间中去,在高维特征空间中运用线性方法提取主成分,再将特征变量从高维向低维映射,保证特征变量得到最大限度的利用,因此使用线性降维后的本征维数小于非线性降维得到的维数。另外,从图中可以看出,基于ISOMAP的预测方法在变量个数为40时,RMSECV值最小为0.150,LLE,LE,PCA和MDS方法提取本征变量个数分为70,60,10和20时,RMSECV值达到最小分别为0.212,0.261,0.238和0.275。结果表明,非线性降维方法得到的RMSECV值比用线性的降维方法得到的小,说明非线性方法提取的本征变量建立的模型预测能力更强,因此非线性降维方法能够更好地揭示实际大米光谱数据的非线性结构。
2.4 非线性建模及预测
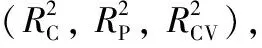
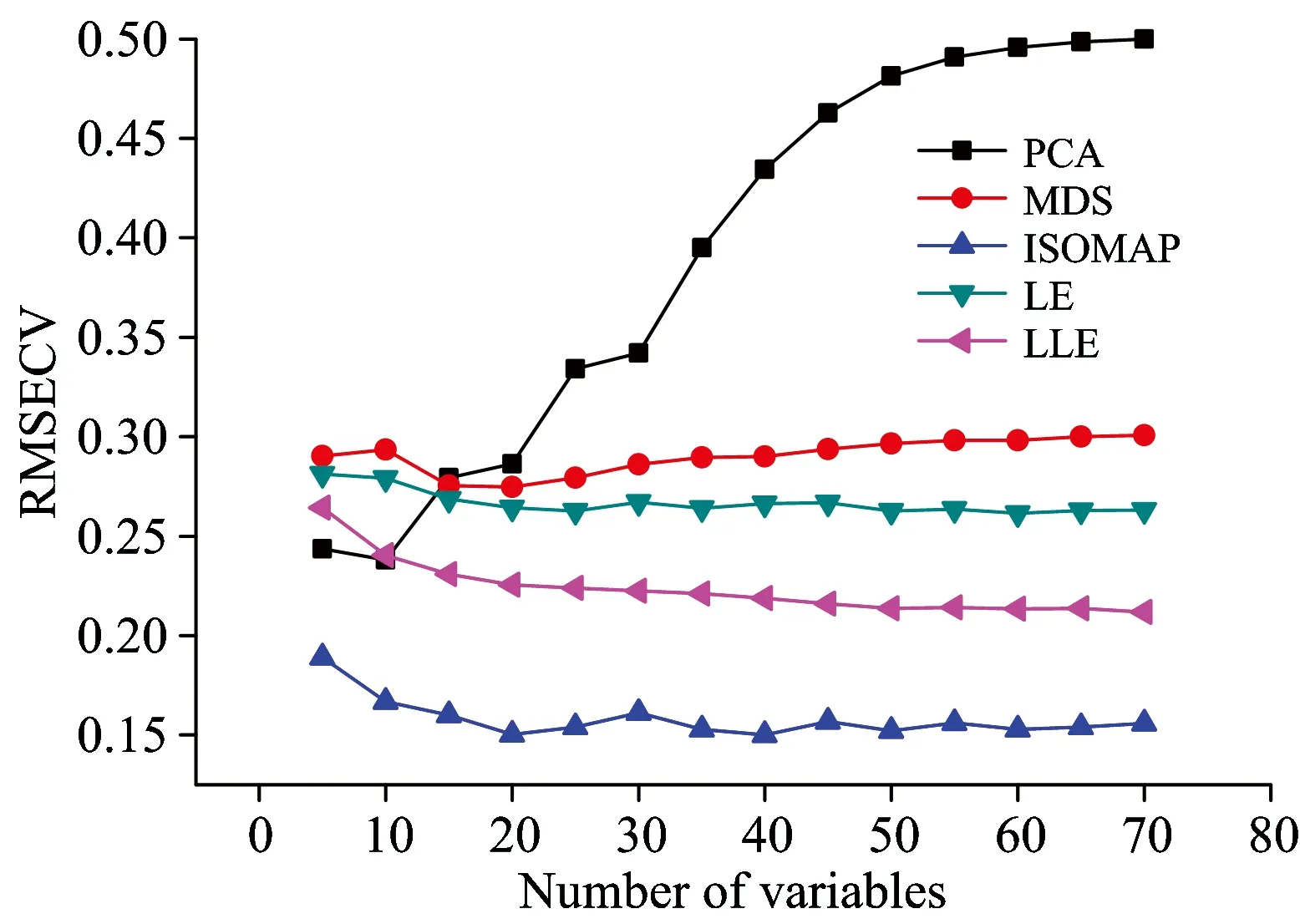
图4 提取得到的本征变量与建模集 样本RMSECV的关系曲线图

表1 使用三种不同的核函数的ISOMAP-KPLS模型在建模、交叉验证和预测过程中获得的预测参数

表2 使用KPLS模型在建模、交叉验证和预测过程中获得的预测参数
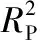
3 结 论
[1] DING Hua, WANG Jing, YAN Wei,et al(丁 华,王 婧,严 伟,等). Hubei Agricultural Sciences(湖北农业科学),2014, 53(24):38.
[2] XIAO Xin, XIE Xin-hua, MAO Xing-xue, et al(肖 昕, 谢新华, 毛兴学,等). Journal of Instrumental Analysis(分析测试学报),2004, 23(4), 43.
[3] WU Di, NIE Peng-cheng, HE Yong,et al(吴 迪,聂鹏程,何 勇,等). Food and Bioprocess Technology(食品与生物加工技术),2012, 5(4):1402.
[4] LI Xiao-li,NIE Peng-cheng, QIU Zheng-jun, et al(李晓丽,聂鹏程,裘正军,等). Expert Systems with Applications(专家系统及其应用), 2011, 38(9):11149.
[5] ZHANG Peng, WANG Dan, LI Jiang-kuo, et al(张 鹏, 王 丹, 李江阔,等). Journal of Food Safety and Quality(食品安全质量检测学报), 2014, 5(4):1191.
[6] WENG Shi-feng, ZHANG Chang-shui, ZHANG Xue-gong(翁时锋, 张长水, 张学工). Journal of Tsinghua University(清华大学学报), 2004, 44(4):485.
[7] TANG Xiao-yan, GAO Kun, NI Guo-qiang(唐晓燕,高 昆,倪国强). Computer Simulation(计算机仿真), 2014, 31(4):347.
[8] SHAO Chao, WANG Chun-hong(邵 超,王春红). Pattern Recognition and Artificial Intelligence(模式识别与人工智能), 2014, 27(2):111.
[9] BAI Jun-qing,YAN Gui-rong,WANG Cheng(白俊卿,闫桂荣,王 成). Journal of Xi’an Jiaotong University(西安交通大学学报),2013, 47(1):85.
[10] LI Yue-jiao,LIU Bing-han(李月娇,刘秉瀚). Journal of Fuzhou University·Natural Science Edition(福州大学学报·自然科学版),2013, 41(2):153.
[11] YUAN De-qiang,ZHAO Rong-zhen(袁德强,赵荣珍). Noise and Vibration Control(噪声与振动控制), 2014, 34(5):150.
[12] CONG Wei,JING Bo,YU Hong-kun(丛 伟,景 博,于宏坤). Journal of Central South University·Science and Technology(中南大学学报·自然科学版),2014, 45(6):1841.
[13] LU Ke-sheng,WANG Ling-zhi(陆克盛,汪灵枝). Journal of Shenyang Agricultural University(沈阳农业大学学报),2013, 44(3):345.
[14] Centner V, de Noordb O E, Massart D L. Analytica Chimica Acta,1998, 376: 153.
[15] Centner V, Verdu-Andres J, Walczak B, et al. Applied Spectroscopy,2000, 54: 608.
[16] Akhlaghi Y, Kompany M. Analytica Chimica Acta,2005, 537(1-2): 331.
(Received Jul. 15, 2015; accepted Nov. 4, 2015)
*Corresponding author
Quick Discrimination of Rice Storage Period Based on Manifold Dimensionality Reduction Methods and Near Infrared Spectroscopy Techniques
LIN Ping1, CHEN Yong-ming1*, ZOU Zhi-yong2
1. College of Electrical Engineering, Yancheng Institute of Technology, Yancheng 224051, China
2. College of Mechanical and Electrical Engineering, Sichuan Agricultural University, Ya’an 625014, China

Rice; Storage period; Manifold dimension reduction; Near infrared spectroscopy
2015-07-15,
2015-11-04
国家自然科学基金项目(31501221,31601227),江苏省自然科学基金项目(BK20140467,BK20161310),江苏省高校自然科学研究面上项目(13KJB210006),盐城市农业科技指导性计划项目(YKN2014009, YKN2014010)资助
林 萍,女,1982年生,盐城工学院电气工程学院讲师 e-mail: binglvcha007@126.com *通讯联系人 e-mail: billrange@126.com
TH744.1
A
10.3964/j.issn.1000-0593(2016)10-3169-05
- 光谱学与光谱分析的其它文章
- Gd靶激光等离子体光源离带辐射及其等离子体演化的研究
- Probing the Binding of Torasemide to Pepsin and Trypsin by Spectroscopic and Molecular Docking Methods
- Mn(Ⅱ)-5-Br-PADAP共沉淀-火焰原子吸收光谱法测定虾、贝样中的镉
- Near Infrared Spectroscopy Study on Nitrogen in Shortcut Nitrification and Denitrification Using Principal Component Analysis Combined with BP Neural Networks
- 内蒙古草原植被最大光能利用率取值优化研究
- 健康和糖尿病大鼠红细胞荧光光谱非线性程度差异

