一种基于色度学的RGBW信号映射算法评价方法
潘定平,金伟其,裘 溯,范秋梅
北京理工大学光电学院,光电成像技术与系统教育部重点实验室,北京 100081
一种基于色度学的RGBW信号映射算法评价方法
潘定平,金伟其*,裘 溯,范秋梅
北京理工大学光电学院,光电成像技术与系统教育部重点实验室,北京 100081
随着对高亮度、低功耗绿色显示技术的不断追求,RGBW显示技术成为了国内外的热门研究方向,已有多种RGBW显示器在市场上开始推广。由于将传统显示器rgb信号转换到RGBW显示器RGBW信号的映射算法不仅需要保留初始颜色,且需要兼容具有不同子像素布局方式的RGBW显示器,因此,信号映射算法成为RGBW显示的关键。在介绍现有的五种信号映射算法的基础上,分析了RGBW显示器中新增的白色子像素对显示颜色的作用方式以及现有四种RGBW子像素布局方式对映射算法显示效果的影响;提出了优秀映射算法应满足的三点要求,并据此推导出优秀映射算法的普适性等式及衡量映射算法亮度提升能力的亮度因子;针对五种映射算法的模拟实验表明:满足普适性等式的映射算法能更好地保留初始颜色的色调和饱和度,亮度因子可有效表征算法对亮度的提升能力。该模型不仅可用于评价现有映射算法,而且可为新型映射算法的研究提供理论指导,使之兼容于具有不同硬件参数和子像素布局的显示器,有助于RGBW显示技术的普及推广。
RGB;RGBW;色度学;白色子像素;子像素布局;算法评价;普适性等式
引 言
液晶电视是当今显示设备的主流,不仅广泛应用于工业、国防等领域,也深入到千家万户的生活中,成为人们居家生活的必备电器设备,然而,传统液晶电视背光源只有5%~10%的能量能够通过液晶屏作用于人眼[1]。随着近几年4K显示器甚至8K显示器热潮的来临,降低液晶屏的能耗成为亟待解决的问题之一。基于LED背光源动态区域控制的液晶电视技术以及RGBW液晶电视技术就是其中较有效且实用化的方法。
RGBW技术是在原有红绿蓝RGB子像素的基础上增加白色W子像素,再通过合适的子像素布局达到高亮度和低功耗的目的。目前国外Hirano Satosh[2],Kwak[3]和Kwon K J[4]等,中国京东方、友达光电和TCL等都提出了各具特色的rgb到RGBW的映射算法。目前RGBW技术推广应用的主要难点之一是与现有的rgb模式兼容问题,即难以从现有的rgb到RGBW的映射算法中选择与不同子像素布局兼容的“最佳”算法。
目前对信号映射算法评价方法的研究不多,王莉莉对映射算法的主观评价实验[1]表明:对于不同的图像和观察环境亮度而言,算法评价结果几乎都不一样,很难挑选出最优的算法。Kwon针对同样的映射算法进行了主观评价实验[4],并针对各算法亮度增益和颜色偏差进行了测试,得到了一个优劣排序。这些研究属于主观评价方法,评价结果易受观察者生理心理、显示设备和周围环境的影响。映射算法的客观评价是目前重要的研究方向。本文将从色度学的角度,研究优秀映射算法的普适性等式,归纳表征映射算法亮度提升能力的亮度因子,研究结果有助于现有映射算法的质量评价和新算法的研究,有利于RGBW显示技术的推广应用。
1 rgb到RGBW映射算法以及子像素布局分析
1.1 rgb到RGBW映射算法
假设r,g,b表示普通显示器中红绿蓝通道的驱动值,R,G,B和W表示RGBW显示器中红绿蓝白通道的驱动值。信号映射算法是基于原有的红绿蓝rgb驱动值计算出白色W驱动值,并生成新的红绿蓝RGB驱动值,从而驱动RGBW显示器的算法。
图1给出RGB显示设备和RGBW显示设备的色域空间,可以看出:加入白色子像素形成的色域空间虽然包含更亮的颜色,但色域空间的变形却不具备简单的函数关系,因此,往往难以在保持颜色的基础上实现rgb信号到RGBW信号的映射。

图1 RGB色域空间(a)和RGBW色域空间(b)
rgb到RGBW的转化在亮度空间进行,本文假设驱动值和亮度的关系满足


(1)
式中,Lc表示对应颜色通道驱动值为c时线性光强尺度的归一化值。
下面简略介绍几种具有代表性的常用映射算法。
1.1.1 算法1
RGBW显示技术最早的映射算法是通过白色子像素来显示所需的颜色亮度
(2)
式中,Y是输入信号在YUV空间中的Y坐标分量。
之后人们发现红绿蓝光谱在Y分量中占的比重相当不均匀,提出了由红绿蓝信号中最小值表示白色信号的思想,具体形式为
(3)
1.1.2 算法2
Hirano Satoshi[2]等提出一种调整红绿蓝通道驱动值的算法
(4)
式中,Lmax=max{Lr,Lg,Lb}。LW有多种计算方式,根据所采用的方法,可进一步细分为算法2-1和算法2-2。
(5)
(6)
1.1.3 算法3
Kwak[3]等提出既然进行信号转换是为了保留颜色,那应通过HSV空间进行转换,即将输入信号转到HSV空间,得到(Hin,Sin,Vin),再进一步提高亮度V
(7)
式中,Vth为预设的阈值,通过阈值得到输出亮度Vout,然后转回RGB空间,并根据输入信号的饱和度、亮度以及一些参数来决定白色子像素的驱动值。
1.1.4 算法4
Kwon K J[5]等提出一种维持图像色彩的算法,其简略形式可表为
(8)
式中,Wo是根据初始信号计算的参量。这种算法否认了以往算法维持色品恒定就能保持色彩的观点,并基于Retinex理论[5],提出描述两幅图像之间色差的指标—平均色差(average color distortion, ACD),以迭代方式修正视频流中下一帧的增益K
(9)
式中,TCD为预设的平均色差阈值;ε是调节反馈速度的比例常数。本文将这一算法应用于固定图像,通过限制色差来确定增益K,ACD是一个与图像背景有关的参量,本文用此算法时选取随机生成的背景。
1.2 子像素布局分析
子像素布局方式是影响RGBW技术显示效果的关键因素之一,目前各厂家都推出了独特的布局方式和信号映射算法。映射算法改变显示光谱特性和强度,影响显示光谱特性和强度的其他因素大致可归结于背光源光谱和彩膜的光谱透过率。
1.2.1 白色子像素的特性
RGBW显示器增加的白色子像素光谱特性是影响信号映射算法显示效果的关键因素。用白光1表示红绿蓝子像素共同形成的白光,白光2表示白色子像素单独发出的白光。虽然色品图[6]中点(0.33, 0.33)周边一定范围内的颜色都可认为是白色,但除非人为地控制彩膜的光谱,否则白光1与白光2并不完全等价,即W≠R+G+B。
图2给出了RGBW显示器42E710U红绿蓝子像素的色品坐标以及白光1(W1)和白光2(W2)的色品坐标。两种白光的色品坐标并不一致,实际上两者的亮度也并不相等。白光2的三刺激值XYZ可表为
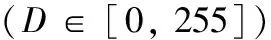
(10)
式中,下标R,G,B,W表示相应通道,D是驱动值,α,β和γ则是由制作工艺决定的客观参数。文献[4]曾简略提过这一点,但并未在色度学理论上给予总结。
前面的五种映射算法都基于W=R+G+B的假设,算法只能在α=β=γ=1的显示器上取得较好的显示效果,为使算法具有较好的兼容性,应该在算法提出时就考虑参数α,β,γ。
1.2.2 子像素布局
白色子像素的加入打破了传统红绿蓝子像素布局的局限,子像素布局的多样性虽然使RGBW显示技术具有更大的改进空间,但也加大了改善信号映射算法兼容性的难度。图3显示了传统的RGB子像素布局和四种流传范围较广的RGBW子像素布局[7-10]。不同的布局方式带来了像素开口率、子像素面积、分辨率以及显示方式上的差别。为了更好地比较,假设五种显示面板都具有相同的显示尺寸。

图2 白色子像素与红绿蓝子像素的关系

图3 RGB布局与四种RGBW布局方式
像素开口率(pixel aperture ratio, PAR)是子像素中通光面积与子像素面积之比。假设图3(a)的像素开口率为PARR,子像素面积为SR。分辨率指包含的逻辑像素数,图3(a)阴影部分表示第二行第二列的一个逻辑像素,具有4×4的分辨率。表1给出五种子像素布局的相关特性。在其他条件相同的情况下,开口率和子像素面积共同决定的通光面积直接影响显示颜色的绝对强度。由于难以获得实际RGBW显示器开口率,本文将以Checkerboard RGBW布局为例,在假设开口率PARR下,说明3SR/4子像素面积对显示效果的影响。
分辨率的不同只代表逻辑像素数目的不同,并不影响信号的映射,只需对输入图像进行插值计算以符合分辨率,进而转换为RGBW信号。逻辑像素中子像素个数只改变映射算法,并不影响具体的转换过程。现有算法都是生成RGBW四个信号,直接应用于图3(b),(c)和(d)布局方式,PenTile RGBW布局中一个逻辑像素拥有10个子像素,采用共享子像素方式工作,图中阴影部分的一对中心逻辑像素红绿需要按信号RG亮度的50%工作,4对边缘逻辑像素蓝白需要按信号BW亮度的12.5%工作。

表1 五种子像素布局的特性
2 基于色品不变的普适性等式
显示器的本质始终是精确显示颜色,而RGBW技术是为了降低功耗,或者说在相同功耗下产生更高的亮度,因此,优秀的信号映射算法需要满足:
(1) 信号转换前后颜色的色品坐标需要保持一致;
(2) 在(1)的基础上适当提升颜色的亮度[11-12];
(3) 保证前两个要求的前提下最大化程度利用RGBW色域空间。
按照色度学理论,驱动值rgb或RGBW都对应着唯一的CIEXYZ坐标,可将驱动值rgb和通过映射算法得到的驱动值RGBW转换到CIEXYZ坐标系,判断转换前后颜色的变化。假设红绿蓝白四个通道的色品坐标不随颜色灰度变化,即任一通道所显示颜色的三刺激值与驱动值之间关系可表为
(11)
式中,Xc,Yc和Zc表示对应颜色通道驱动值为c时的三刺激值,Xc=255,Yc=255和Zc=255表示c通道驱动值最大也就是255时的三刺激值。
对于RGB显示器,当显示颜色满足各基色叠加且第i个像素输入驱动值为(r, g, b)时,对应的三刺激值可表为
(12)
式中,Xi,Yi和Zi为RGB显示器第i个像素的三刺激值。
对于RGBW显示器,若第I个像素输入驱动值为(R, G, B, W),对应的三刺激值可表为
(13)
式中,XI,YI和ZI为RGBW显示器第I个像素的三刺激值。
通常,RGBW显示器和RGB显示器的红绿蓝子像素之间有因背光源、彩膜光谱和子像素布局造成的强度差别。以棋盘式布局RGBW显示器为例,由表1可知,其子像素面积只有RGB显示系统的75%,两台显示器红绿蓝子像素之间的关系可表为
(14)
式中,4/3表示子像素布局中子像素面积造成的强度差别,9个Ω参数表示背光源和彩膜等因素决定的参量,用3×3矩阵Ω表示,Ω中出现负值表示RGBW显示器的色域三角形没能包含RGB显示器的色域,即RGBW显示器不能显示RGB显示器的部分颜色。
于是,式(12)和式(13)可分别简化为
(15)
(16)
可以看出,只要RGB和RGBW显示器的驱动值(r, g, b)和(R, G, B, W)满足
(17)
就可保证所显示的颜色不论是亮度还是色品都保持不变。
映射算法的第二点要求是在保持颜色色品坐标的前提下适当提升亮度,根据式(15)和式(16)进行颜色色品的计算可得
(18)
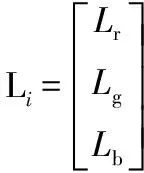
(19)
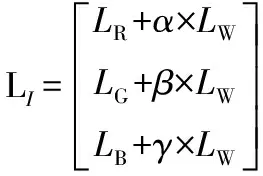
式中,xi,yi和zi为RGB显示器中第i个像素的色品坐标,xI,yI和zI为RGBW显示器中第I个像素的色品坐标,矩阵X=[XR=255,XG=255,XB=255],Y=[YR=255,YG=255,YB=255],Z=[ZR=255,ZG=255,ZB=255]。为了保持色品坐标的恒定,信号映射算法需使驱动值满足
(20)
式中,n表示任意一个正实数。
显然,式(20)是一个能够衡量信号映射算法能否保持颜色色品不变的普适性等式。对于式(17)的示例,当n=4/3时表示转换前后颜色色品与亮度都一致,即当n大于或小于4/3时表示转换前后颜色色品一致,但亮度有所增加或减弱,本文将n称为亮度因子。需要指出,亮度因子n并不固定是4/3,它取决于背光源的光谱强度和子像素布局等因素;对不同布局的显示器,同一算法对某些颜色可能提升或降低亮度,脱离具体显示器谈论算法的优劣没有实质性意义。
如果假设RGB显示器与RGBW显示器的红绿蓝子像素除子像素面积外,具有完全相同的显示效果,即矩阵Ω是单位矩阵;RGBW显示器中白光1和白光2具有相同的色品坐标,即α,β和γ满足α=β=γ=t(t往往等于一个略大于1的常数,这里假设t=1);用r,g,b,R,G,B和W代表光强尺度的值Lc,则式(20)可简化为
(21)
3 基于普适性等式的映射算法分析
为了验证维持信号色品的普适性等式(20),先对现有的五种映射算法进行结构上的分析,挑选出符合等式的算法,再通过模拟实验判断算法的性能。
本文算法都基于α=β=γ=1和Ω=I的假设,优秀映射算法需满足简化的普适性等式(21),对算法1~4进行结构转换可知,只有算法2和算法4满足普适性等式,可认为其本质是一样的,不同点在于算法2通过选取合适的W确定亮度因子,算法4通过迭代的方式限制色差确定亮度因子,具体形式为
(22)
由于色品坐标不变等价于色调和饱和度不变[7],为了证明算法2和算法4具有更好的映射效果,选取一系列颜色(r, g, b)进行映射算法的转换,rgb取0, 40, 80, 120, 160, 200, 240和255中的任意值,排除无色调定义或色调等于0(即g=b)的组合,共计还有448种颜色,分别对其应用5种映射算法,得到算法对颜色亮度增强、色调改变、饱和度改变等能力如图4所示,其中,横坐标代表448种颜色按饱和度从小到大的排列,纵坐标亮度增益指颜色转换前后V的增益,纵坐标色调差值和饱和度差值分别定义为
(23)
式中,H*和S*是经算法处理得到的色调和饱和度,Ho和So是初始颜色的色调和饱和度。
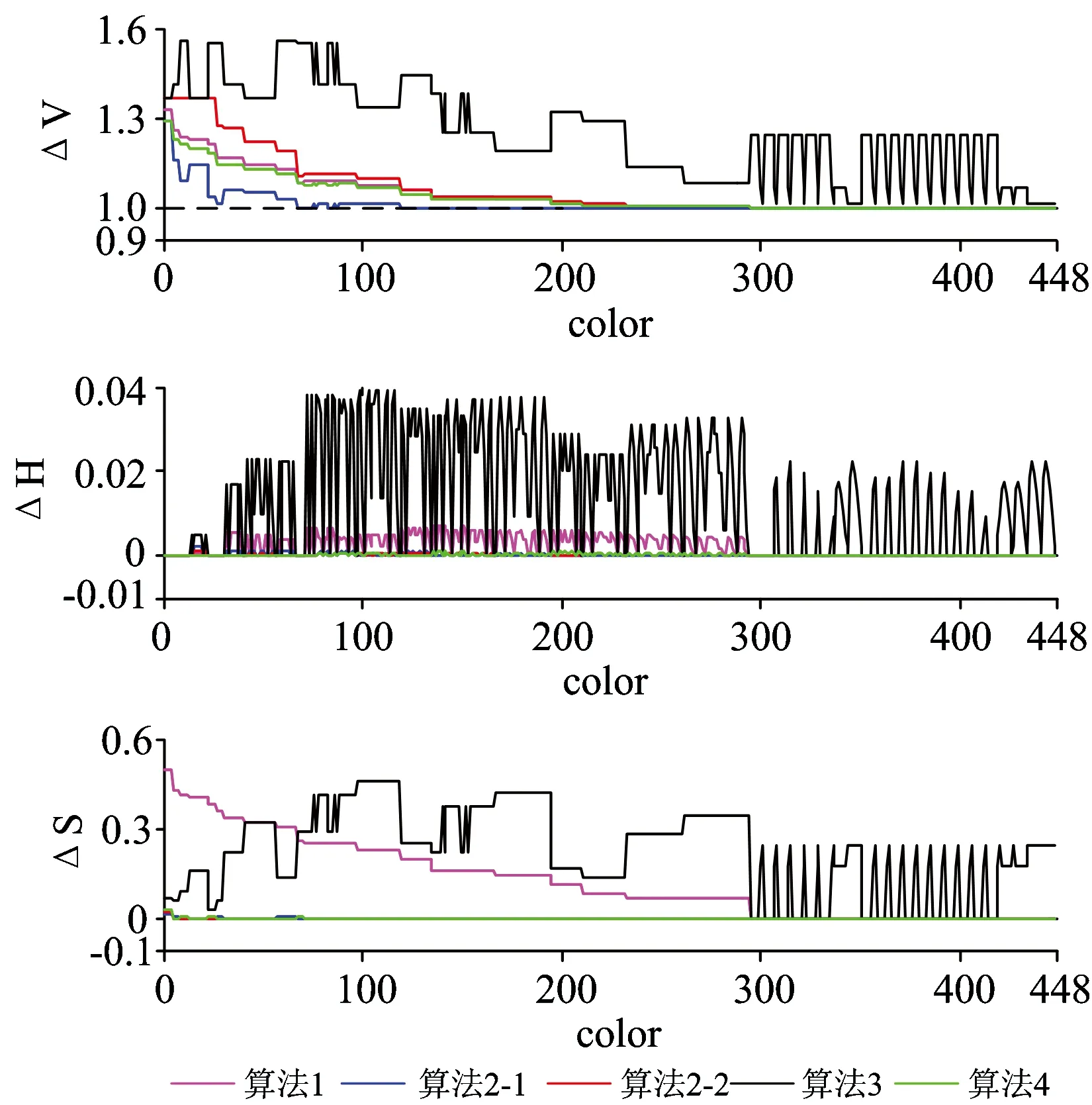
图4 映射算法对亮度、色调和饱和度的改变能力
由图4对五种映射算法的亮度提升、色调和饱和度改变能力进行分析:
(1) 五种映射算法对所有颜色的亮度提升能力都大于1,且随着初始信号颜色饱和度的增大而减小,这是为了保留高饱和度颜色的纯度,算法降低了白色子像素的利用率,从而降低了亮度增益;仅就亮度提升优劣的算法排序为算法3,算法2-2,算法1,算法4,算法2-1。
(2) 算法3针对不同颜色的色调改变程度上下波动很大,对初始颜色的改变最为明显,算法1次于算法3,算法2-1、算法2-2和算法4几乎都能完美地保留初始颜色的色调和饱和度。
可以看出,算法1和算法3虽然具有较大的亮度提升能力,但却不满足映射算法的第一点基本要求,所以不适用于RGBW显示器,只有符合本文提出的普适性等式的算法2和算法4,符合映射算法的前两个基本要求。
为了进一步验证普适性等式,采用颜色(150, 190, 210),(140, 200, 160)和(200, 170, 70)进行实际的信号映射。虽然本实验的显示器不能同时显示RGB和RGBW图像,但由于α=β=γ=1且Ω=I,可将信号(R, G , B, W)以(R+W, G+W, B+W)的形式显示在普通RGB显示器上,又因为RGB显示器不具备RGBW显示器高亮度的特点,将转换前后的信号(r, g, b)和(R+W, G+W, B+W)在亮度维度上除以2(假设两台显示器的红绿蓝像素完全一致),便可在牺牲绝对亮度的基础上,在普通显示器上显示出信号转换前后的相对效果。原始颜色和通过5种映射算法得到的颜色如图5所示,表2给出了对应的颜色参数,其中RGBW信号在颜色空间HSV的坐标值根据信号(R+W, G+W, B+W)转换。
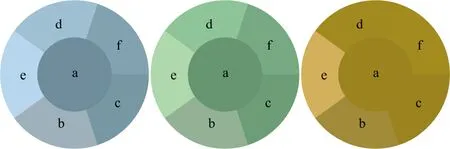
图5 初始颜色和不同映射算法转换后颜色
结合图5和表2可知:算法1(b)和算法3(e)虽在提高亮度方面具有较好表现,但算法1(b)损失了饱和度,算法3(e)损失了色调,均导致较大色差。算法2-1(c)和算法2-2(d)和算法4(f)基本有效保留了原始颜色(色调和饱和度)。算法2-1(c)亮度提高能力不明显,特别是映射饱和度较高的颜色(200, 170, 70)时,映射结果与初始颜色完全一致,算法4(f)的亮度提高能力居中,算法2-2(d)的亮度提高最大,但也带给了观察者较大的视觉误差;算法2和算法4的亮度因子n(由于两台显示器的红绿蓝像素完全一致,因此只要n>1便表示提升亮度)大小排序与亮度V一致,即n能够衡量映射算法对亮度的提高程度。因此,对于示例的三种颜色,五种算法中满足普适性等式的算法2和算法4更为优秀,这与第一组实验结果一致。

表2 算法转换前后颜色的具体参数
王莉莉的主观评价实验[1]包含了算法2-1和算法2-2,结果是大多数情况下算法2-2优于算法2-1,唯有在显示中等亮度和高彩度的图像时,算法2-1具有更好的表现。算法2-1、算法2-2和算法4是Kwon评价实验[4]选取的算法,实验结果与本文基本一致,不同点在于算法4具有比算法2-2更高的亮度和更好的颜色保留能力,鉴于算法4对亮度的提升效果很大程度上取决于图像背景的选取,所以这一不同是可以理解的。
普适性等式的推导过程考虑了显示器的具体参数,不仅可用于新算法的研究,也可用来修改满足等式的已有算法,使之能够应用于具有不同硬件参数和子像素布局的显示器,以获得更好的显示效果,如算法2和算法4的普适形式可分别表为
(24)
(25)
4 结 论
RGBW显示技术的推广依赖于优秀的信号映射算法,为了兼容层出不穷的子像素布局,本文提出了优秀映射算法的普适性等式和表征映射算法亮度提升的亮度因子n。普适性等式既有助于对现有映射算法的评价,也有助于改善现有映射算法的兼容性,可为新型映射算法的研究提供理论指导,有利于促进RGBW显示技术的发展和应用推广。
模拟实验表明:只要rgb到RGBW的映射算法满足普适性等式,就可满足信号映射算法三点要求中的前两点,即在保持颜色色品的前提下提高颜色亮度;第三点要求是最大化程度利用RGBW颜色空间,这取决于白色子像素的参与程度,即映射算法在转换不同颜色时亮度因子n的取值,过小的n会导致亮度提升不明显,而过大的n又可能会使人眼产生色差,所以n的取值实际上是一个与人眼视觉有关的问题。为了使每一种颜色的亮度提升程度能够让观察者有较为舒适的感觉而又不至于产生明显的色差,可通过主观评价实验进行研究,也可通过限制CIE色差来达到目的。这是未来需要进一步研究的重要方向。
[1] WANG Li-li, TU Yan, CHEN Li, et al. SID International Symposium, Digest of Technical Papers, 2007, 38(1): 1142.
[2] Hirano Satoshi. European Patent: WO0137249, 2001.
[3] Kwak Youngshin, Park Juyong, Park Du-Sik. Applied Optics, 2008, 47: 4491.
[4] Kwon K J, Kim Y H. Display Technology, 2012, 8(12): 684.
[5] Land E H. Vision Research, 1986, 26(1): 7.
[6] JIN Wei-qi, HU Wei-jie(金伟其, 胡威捷). Radiometry Photometry Colorimetry and Measurement(辐射度光度与色度及其测量). Beijing: Beijing Institute of Technology Press(北京: 北京理工大学出版社), 2006. 112.
[7] Arnold A D, Castro P E, et al. Journal of the Society for Information Display, 2005, 13(6): 525.
[8] Lee B W, Park C, Kim S, et al. SID International Symposium, Digest of Technical Papers, 2003, 34(1): 1212.
[9] Lee B, Song K, Yang Y, et al. SID Symposium Digest of Technical Papers, 2004, 35(1): 111.
[10] Brown Elliott C H, Credelle T L, Higgins M F. Information Display,2005, 21: 26.
[11] QU Chao-hui(屈朝辉). Advanced Display(现代显示), 2012, 23(9): 64.
[12] Miller M E, Murdoch M J. Journal of the Society for Information Display, 2009, 17(3): 195.
*Corresponding author
(Received Jul. 21, 2015; accepted Nov. 28, 2015)
RGBW Signal Mapping Algorithm Assessment Based on Colorimetry
PAN Ding-ping, JIN Wei-qi*, QIU Su, FAN Qiu-mei
MOE Key Laboratory of Photoelectronic Imaging Technology and System, School of Optoelectronics, Beijing Institute of Technology, Beijing 100081, China
With the continuous pursuit of high brightness and low power consumption display technology, RGBW display technology has been attracting increasing attention in the world. Various kinds of displays based on this technology have been produced in the market. The key of this technology is signal mapping algorithm which converts RGB signal into RGBW signal without color distortion and compatible with different sub-pixel layouts. This paper, on the basis of five kinds of signal mapping algorithms, analyzes the mode of action of newly added white sub-pixel affects display color, and the display performance affected by four kinds of sub-pixel layouts; it proposes the corresponding condition of excellent signal mapping algorithm based on colorimetry and deduces the universal equation of excellent signal mapping algorithm and brightness factor which could measure the ability of enhancing brightness. The simulation experiment shows that the signal mapping algorithm which satisfies universal equation could be able to maintain the hue and saturation better. The signal mapping algorithm’s ability to enhance brightness is effectively characterized by brightness factor. In conclusion, the proposed universal equation can be used to evaluate existing signal mapping algorithms, and it provides theoretical references for the research of new signal mapping algorithm which could be compatible with different hardware parameters and sub-pixel layouts, promote the popularization of RGBW display technology.
RGB; RGBW; Colorimetry; White sub-pixel; Sub-pixel layout; Algorithm assessment; Universal equation
2015-07-21,
2015-11-28
国家自然科学基金重点项目(61231014)和高等学校博士学科点专项科研基金项目(20131101130002)
潘定平,1992年生,北京理工大学光电学院硕士研究生 e-mail: dingping.pan@139.com *通讯联系人 e-mail: jinwq@bit.edu.cn
TN27
A
10.3964/j.issn.1000-0593(2016)10-3119-08
- 光谱学与光谱分析的其它文章
- Gd靶激光等离子体光源离带辐射及其等离子体演化的研究
- Probing the Binding of Torasemide to Pepsin and Trypsin by Spectroscopic and Molecular Docking Methods
- Mn(Ⅱ)-5-Br-PADAP共沉淀-火焰原子吸收光谱法测定虾、贝样中的镉
- Near Infrared Spectroscopy Study on Nitrogen in Shortcut Nitrification and Denitrification Using Principal Component Analysis Combined with BP Neural Networks
- 内蒙古草原植被最大光能利用率取值优化研究
- 健康和糖尿病大鼠红细胞荧光光谱非线性程度差异

