应用混合种群遗传神经网络的精梳毛纺工艺参数反演模型

杨建国, 熊经纬, 徐 兰, 项 前

(东华大学 机械工程学院, 上海 201620)

应用混合种群遗传神经网络的精梳毛纺工艺参数反演模型

杨建国, 熊经纬, 徐 兰, 项 前

(东华大学 机械工程学院, 上海 201620)

针对传统精梳毛纺工艺参数反演模型收敛性和稳定性不理想、反演精度低等问题，以及标准遗传算法(SGA)应用于复杂优化问题时存在早熟收敛等缺点，以BP神经网络为基础，提出一种混合种群遗传人工神经网络(MPG-ANN)反演模型，首先以混合种群遗传算法优化BP神经网络的权值与阈值建立预测模型，在此基础上根据毛纱CV值建立混合种群遗传算法反演模型，用来反演精梳毛纺生产过程工艺参数。以纺纱车间大量现场工艺检测数据为对象进行反演验证，结果表明：MPG-ANN模型反演精度达97%，相比于标准遗传算法人工神经网络(SGA-ANN)模型提高4%，同时反演结果波动幅度相比于SGA-ANN模型降低了6.28%。该方法可为精梳毛纺生产过程质量控制提供有效的理论指导，对纺织企业新产品工艺开发设计的快速决策具有很好的借鉴作用。

精梳毛纺工艺； 遗传算法； 混合种群遗传人工神经网络； 工艺参数反演

纺织品加工是一种典型的复杂非平稳加工过程，常见的纺织品原料加工包括初加工、前纺、后纺、织布及染整等几大工序，其加工过程受到内外环境的扰动，不但包括材料位移过程，流体动力学过程，而且包括复杂的热交换与化学反应。为实现对纺织品加工质量的准确预测与控制，国内外许多学者开展了研究与实践，并取得了丰硕的成果[1-3]。 纺织生产过程的预测模拟可表达为模型参数的非线性函数，因而其反演也可归为非线性最优化问题[4-6]。近年来，以遗传(genetic algorithm,GA)算法、BP (back propagation)人工神经网络等为代表的全局优化算法成为了国内外反演领域的研究热点[7-9]。文献[10]采用直接逼近法反演棉花模型所需的初始数据及参数，该方法将遥感信息和棉花模型相结合，建立针对遥感-棉花的反演模型，实验结果表明该反演模型是可行的。传统的参数反演算法存在收敛性和稳定性不理想，反演精度低，计算速度较缓慢等问题，以及标准遗传算法(standard genetic algorithm,SGA)存在的早熟收敛等缺点，本文提出采用混合种群遗传算法(mixed population genetic algorithm, MPGA)优化BP神经网络的权值和阈值来建立遗传神经网络正演模型，在此基础上根据毛纱CV值来建立混合种群遗传算法反演模型，用来反演生产过程工艺输入参数。

1 纺织品工艺参数反演问题描述

对于毛纺精梳细纱生产而言，制约产品质量的2大要素包括原料的性能参数与加工工艺参数，当工艺过程中的输出目标参数确定后，通过反演模型寻找可能工艺参数组合，再根据生产成本与效率进行筛选，得到最优工艺参数组合，提高工艺设计的针对性。本文要解决的纺织工艺参数反演问题为:已知部分输入工艺参数和输出目标参数，通过构造反演模型，反演出能满足相同输出的大量可选输入参数组合，为确定最优工艺参数奠定基础。

2 混合种群遗传算法分析

2.1 传统遗传算法缺陷分析

交叉概率c与变异概率m控制染色体交叉和变异发生的频率，合适的取值对遗传算法全局与局部搜索能力有很大的影响，不恰当的c、m取值可能会导致遗传算法的未成熟收敛。

SGA算法的优化性能受到群体规模的制约，较小的规模会导致进化不成熟，个体之间竞争强度变弱，导致群体在进化的过程中很快趋于单一化，群体很快便终止了进化;较大的规模则会造成计算效率的下降。

最大迭代次数是传统遗传算法进化终止的条件，不恰当的设置会导致进化不充分，造成整个种群的未成熟收敛。

2.2 混合种群遗传算法优势分析

SGA算法的控制参数主要包括交叉概率c与变异概率m，对于算法的全局与局部搜索能力有很大的影响，他们的取值方式有无数种，不同的选择得到的优化结果差异很大。MPGA通过不同控制参数多个种群的同时进化，充分进行全局和局部搜索，使得算法的泛化性能得到提高。

MPGA算法中的各个种群是相对独立的，通过移民算子相互联系。移民算子是指定期将各种群在进化过程中产生的最优个体移入其他的种群中，即将目标种群中的最差个体用源种群的最优个体代替，实现种群间的信息交换，不至于过早陷入早熟状态。

建立精华种群，最优个体通过人工算子选择并保存在精华种群内，为保持其内个体不变性，不对精华种群进行交叉变异等操作。图1示出MPGA算法结构示意图。

3 数学模型

工艺参数反演方法数学模型抽象描述如下：

1)设O={o1,o2,…,on}，是纺织生产过程中n(n>1) 个不同加工工艺参数的集合，其中参数on可由o1,o2,…,on-1参数的组合预测得到。

2)假设op,oq(p=1,2,…,n-1；q=1,2,…,n-1)是对纺织加工质量有着重大影响的参数，实际生产中该参数只有很少的数量，为了通过反演得到更多的参数op,oq，将一组o1,o2,…,on-1数据作为网络训练输入，on作为网络输出，将训练好的网络封装成一个函数f(o1,o2,…,on-1)=on，即任意给定一组o1,o2,…,op,…,oq,…,on-1可通过该神经网络封装函数计算得到on。

3)构建混合种群遗传算法，将op,oq编码成染色体，组成各种群中的单独个体，令g(o1,o2,…,on-1)=f(o1,o2,…,on-1)-(on)真实值;则目标函数可表示为g(o1,o2,…,op,…,oq,…,on-1)的绝对值的最小值，从而得到反演参数op,oq。

4 精梳毛纺反演算法设计

4.1 反演算法基本步骤

1)基于已知精纺毛纱样本的纤维直径离散系数(离散系数)、毛条含油量、粗纱捻系数、毛条回潮率、纤维长度(豪特长度)、锭速、细纱牵伸倍数、纤维直径(平均线直径)、细纱钢丝圈质量、纤维质量不匀率等条件。结合混合种群遗传算法神经网络算法建立针对初始毛纱CV值的预测模型。

2)根据建立的初始精纺毛纱CV值预测模型得到预测结果，可以得到实际数据与计算数据的均方根误差，若满足精度要求则迭代结束，否则继续迭代直至精度符合要求。

3)基于当前正演模型，通过混合种群遗传算法构造其反演模型，用来反演关键工艺参数。

4)以CV值实测数据与预测数据的差作为适应度函数的值，通过迭代寻优，得到最佳工艺参数组合。

5)根据正演模型计算CV值预测数据，从而得到目标函数值，根据目标函数值的精确度得到最合适的工艺参数。

4.2 MPG-ANN算法设计

1)种群初始化。开始阶段，多个种群同时进行进化，各种群具有不同的交叉概率与变异概率以实现不同的搜索。每个种群中的个体由待优化参数编码而成的染色体组成，染色体采用十进制编码方法，每个数码由4位二进制数码表示。染色体个体包括了神经网络全部权值和阈值。

染色体结构由BP神经网络的权值和阈值编码组成：

[w111,…,w11m,…,w1i1,…,w1im,w1n1,…,w1nm,b11,…,b1n,w211,…,w21n,…,w2j1,…,w2jn,w2k1,…,w2kn,b21,…,b2k]式中:w1ij为输入层-隐含层神经元权值矩阵W1(m×n维)中的任意元素;b1i为输入层-隐含层神经元阈值矩阵B1(n×1维)中的元素;w2ij为隐含层-输出层神经元权值矩阵W2(n×k维)中的元素;b2i为隐含层-输出层神经元阈值矩阵B2(k×1维)中的元素。

2)适应度函数的确定。对于给定的训练数据与实际数据，将实际数据与预测数据的平均绝对误差定义为适应度函数f，按式(1)所示。

(1)

式中:N为网络输出的节点个数即预测值个数;yi为网络第i个节点的实际数据(即期望输出);oi为第i个节点的预测输出。

3)算子选择。设每个种群由N个个体组成，且每个个体x对应的适应度值为f(x)，则选中x的概率见式(2)。

(2)

根据px的大小，选择操作采用轮盘赌法。

(3)

(4)

式中μ为(0,1)之间产生的随机数。

5)确定变异算子。m决定了算法的局部搜索能力，为搜索的更为细致，每个种群被随机赋予变异概率，范围限制在[0.001,0.05]区间内。对第i个个体的第j个基因aij按式(5)进行变异操作。

(5)

式中:(amin,amax)为基因aij的最小与最大值，即上下界;f(g)=r2(1-g/Gmax)2，r2为随机数，g为当前的迭代次数，Gmax为最大迭代次数;r为[0,1]之间的随机数。

6)移民算子。移民算子是将各种群联系起来的重要步骤，其基本思想是将不同种群产生的不同最优个体相互转移，即将其他种群中的最差个体用转移来的最优个体代替，最大限度地保证了各种群之间的紧密联系。

7)精华种群。通过筛选函数将每一代种群当中的最优个体筛选出来并放入精华种群中保存。其内的个体在随后的进化过程中不再发生变化，以最大限度保证最优个体的完整性。最终以进化代数作为终止的依据。

4.3 MPG算法反演

4.3.1 产生初始混合种群

程序的开始阶段需要进行种群的初始化，每个种群中的染色体左边部分由需要反演的参数在输入部分的从左往右顺数的位置确定，由a，b表示，如产生a=2，b=7，则表示需要对毛条含油量和细纱牵伸倍数进行反演，一旦确定后，种群中a，b的值就此固定;右边部分随反演参数个数不同而不同，若反演参数个数为2，则在一定范围内随机产生1行16列的0、1数值矩阵来初始化种群。

4.3.2 选 择

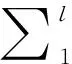
4.3.3 交叉变异

交叉及变异都是形成新个体的一种有效方法，其优点是能够避免部分信息丢失，最大限度的保证了遗传算法的有效性。

反演算法部分交叉与变异操作采用正演算法部分的相同操作，不同点在于染色体的编码方式。混合种群遗传算法反演流程如图2所示。

5 应用实例

以某公司的精纺毛纱中毛条含油量和细纱牵伸倍数的反演为例说明本文算法的实现过程。首先建立毛纱CV值的正演模型，其中输入的工艺参数为纤维直径离散系数(离散系数)、毛条含油量、纤维质量不匀率、粗纱捻系数、毛条回潮率、锭速、细纱牵伸倍数、细纱钢丝圈质量、纤维直径(平均直径)、纤维长度(豪特长度)。输出参数为毛纱CV值， 已知精纺毛纱的生产数据，选取60组样本作为训练数据集，5组样本作为预测模型测试数据集。剩余10组作为反演测试数据集。

5.1 毛纱CV值预测模型训练

运用MatLab软件编写相关程序，神经网络预测模型算法参数设定:输入神经元数m=10，输出神经元数n=1，隐含层神经元个数设为7[4]，训练函数trained，隐含层函数tansig，输出层函数purelin，混合种群遗传算法相关参数设置为:种群数目M=20、每个种群包含的个体数目I=40、进化代数G=100。首先利用已给的数据样本进行MPG-ANN的预测模型训练，其适应度函数迭代曲线如图3所示。为比较MPG-ANN预测模型具有更好的预测性能，同时给出SGA模型的适应度函数值迭代曲线，如图4所示。

从图4可看出，当进化代数达到70代以后，预测结果的适应度函数值(即平均绝对误差)逐渐趋于稳定，约为1.2，表明每个个体都在最优解附近。SGA适应度函数值从60代之后逐渐稳定在1.7左右，且曲线的平稳性要差于MPG-ANN，说明MPG-ANN在预测毛纱CV值的精度上要好于SGA模型。

5.2 精梳毛纺参数反演结果分析

神经网络预测模型训练好以后，通过建立的MPG-ANN反演模型反演毛条含油及细纱牵伸倍数2个参数。MPG-ANN反演模型主要参数设定为:种群数目M=30、每个种群包含的个体数目I=40、进化代数G=100。每个种群的交叉概率及变异概率在一定的范围内随机产生。为比较MPG-ANN反演模型的反演效果，同时给出SGA模型最优反演结果与对应毛纱CV值预测结果作为对比，结果如表1～3所示。

表1 毛条含油参数反演结果

表2 细纱牵伸倍数参数反演结果

表3 反演结果毛纱CV预测值

1)从参数反演精度上看，SGA模型毛条含油10组结果的平均相对误差为6.957 3%，细纱牵伸倍数的平均相对误差为6.089 1%，而MPG-ANN模型反演的平均相对误差分别为2.873 4%与2.719 8%。相对于SGA算法分别降低4.083 9%与3.369 3%，由此可知MPG-ANN模型在精梳毛纺参数的反演精度上要高于SGA模型。

2)从统一参数反演的结果稳定性上来看，MPG-ANN模型毛条含油参数的最大反演相对误差为4.938 4%，最小相对误差为1.464 1%，波动的最大幅度即为3.474 3%;细纱牵伸倍数的最大反演相对误差为4.132 0%，最小相对误差为0.923 3%，波动的最大幅度即为3.208 7%;同样，从表2、3中可以得出，SGA模型的2种参数反演结果的最大波动幅度分别为9.755 5%、3.575 3%，MPG-ANN模型的波动幅度相比于SGA-ANN模型最多降低6.281 2%，由此可知，MPG-ANN在精梳毛纺参数的反演结果稳定性上要优于SGA模型。

3)为说明MPG-ANN模型的泛化性能，在得到2种参数反演结果的基础上，与其他已有参数进行组合，作为MPG-ANN与SGA模型的预测样本，对毛纱CV值进行预测，结果如表4所示。从表中可以看出MPG-ANN模型预测结果的平均相对误差相对于SGA模型降低4.249 8%，说明MPG-ANN模型的泛化性能要优于SGA模型。

从反演结果及对应预测结果可以看出，MPG-ANN反演模型相比于SGA反演模型具有更高的反演精度和较好的泛化能力，能够对精梳毛纺工艺生产中关键参数进行反演，并达到理想的精度要求。

6 结 论

针对纺织生产过程中部分工艺参数对纺织产品质量有重要影响但又不易获得的情况，以混合种群遗传算法优化BP神经网络权值与阈值建立正演模型，在此基础上，通过混合种群遗传算法反演模型对工艺参数进行寻优，以实际纺织生产过程参数进行模型测试，验证了该反演模型的有效性。

FZXB

[1] 李翔,彭志勤,金凤英,等.基于神经网络的精纺毛纱性能预测模型比较[J].纺织学报,2011,32(3):51-56. LI Xiang, PENG Zhiqin, JIN Fengying, et al. Comparing prediction models for worsted yarn performances based on neutral networks[J]. Journal of Textile Research, 2011,32(3):51-56.

[2] SUBHASIS Das, ANINDYA Ghosh, ABHIJIT Majumdar, et al. Yarn engineering using hybrid artificial neural network-genetic algorithm model [J]. Fibers and Polymers, 2013, 14 (7): 1220-1226.

[3] JI Mwasiagi, HUANG XiuBao,WANG XinHou. The use of hybrid algorithms to improve the performance of yarn parameters prediction models [J]. Fibers and

Polymers, 2012, 13(9): 1201-1208.

[4] 刘彬,项前,杨建国, 等.基于遗传神经网络的纱线质量预测[J].东华大学学报,2013,39(4):504-508. LIU Bin, XIANG Qian, YANG Jianguo, et al. Combining the genetic algorithm with artificial neural networks for yarn quality forecasting[J]. Journal of Donghua University, 2013,39(4):504-508.

[5] GUILLAUME Ramillien. Genetic algorithms for geophysical parameter inversion from altimeter data[J]. Geophysical Journal International, 2001(2):393-402.

[6] 刘斌,李术才,李树忱,等. 基于不等式约束的最小二乘法三维电阻率反演及其算法优化[J]. 地球物理学报,2012(1):260-268. LIU Bin, LI Shucai, LI Shushen, et al. 3-D electrical resistivity with least-squares method based on inequality and its computation efficiency optimization.[J]. Chinese Journal of Geophysics,2012(1):260-268.

[7] HONN Kao, PEIRU Jian. Seismogenic patterns in the Taiwan region:insights form source parameter inversion of BATS data[J].Tectonophysics,2001,333:179-198.

[8] 施建成,杜阳,杜今阳,等. 微波遥感地表参数反演进展[J]. 中国科学:地球科学,2012(6):814-842. SHI Jianchen, DU Yang, DU Jinyang, et al. Microwave remote sensing of the earth′s surface parameters inver-sion[J]. China Science: Earth Science, 2012(6):814-842.

[9] 田明俊,周晶. 岩土工程参数反演的一种新方法[J]. 岩石力学与工程学报,2005(9):1492-1496. TIAN Mingjun, ZHOU Jing. New algorithm for parameter inversion in geotechinical engineering[J]. Chinese Journal of Rock Mechanics and Engineering,2005(9):1492-1496.

[10] 赵艳霞,秦军,周秀骥. 遥感信息与棉花模型结合反演模型初始值和参数的方法研究[J]. 棉花学报,2005(5):280-284. ZHAO Yanxia, QIN Jun, ZHOU Xiuji. Study on combinations of remote sensing and cotton model to retrieve initial inputs and parameters[J]. Cotton Science,2005(5):280-284.

Worsted spinning process parameters inversion model using mixed population genetic neural network

YANG Jianguo, XIONG Jingwei, XU Lan, XIANG Qian

(CollegeofMechanicalEngineering,DonghuaUniversity,Shanghai201620，China)

Inversion model of conventional worsted spinning process parameters is defective because of unsatisfactory convergence and stability and low inversion accuracy. Besides, standard genetic algorithm shows premature convergence in the application of complicated optimization problem. Therefore, the paper put forward an inversion model of mixed population genetic-artificial neural network based on BP neural network. First the author established the prediction model by optimizing the weights and threshold of BP neural network through mixed population genetic algorithm. On this basis, the author created the inversion model of mixed population genetic algorithm according to the coefficient of variation (CV) value of yarn and used it for the inversion of process parameters during worsted spinning production. Next, the author conducted inversion verification by taking a large quantity of test data of field process in spinning workshops field process parameters. The results show that the inversion accuracy of MPG-ANN model reaches 97% and increases by 4% relative to SGA-ANN model. In addition, the fluctuating margin of the inversion results of MPG-ANN model reduces by 6.28% at most relative to SGA-ANN model. Finally, the author predicted the CV value of yarn on the basis of inversion results. This method not only has an important guiding role in the textile production process quality control, but also has a very good reference for enterprises rapid process development of new product design decision.

worsted spinning process; genetic algorithm; mixed population genetic-artificial neural network; parameters inversion

10.13475/j.fzxb.20150400706

2015-04-08

2016-01-07

国家自然科学基金资助项目(51175077)作者简介：杨建国(1951—),男,教授,博士。主要研究方向为光机电一体化和智能机器人、智能制造与控制。E-mail:jgyangm@dhu.edu.cn。

TS 101.1

A