基于绿色模块划分的EHMODDPPSO不确定优化方法
胡浩平
(深圳信息职业技术学院财经学院, 广东 深圳 518172)
基于绿色模块划分的EHMODDPPSO不确定优化方法
胡浩平
(深圳信息职业技术学院财经学院, 广东 深圳 518172)
摘 要:针对模块划分过程中基本单位本身是一个零件库的情况,研究了零件库中零件属性呈标准正态分布随机数等不确定性问题,分析模块与模块的功能和结构相关性及其本身作为零件库的前提下所属零件本身绿色性,构建了包含内聚度、耦合度、绿色度三个目标函数的产品绿色模块划分的不确定性优化模型,设计一种EHMODDPPSO方法,求出最优模块划分以及相应各零件表中最优零件。以一个轮式装载机部分模块为实例,验证了其合理可行性,面对日益丰富的零件以及其多样属性,本研究具有较好的实用价值。
关键词:不确定优化;随机数;模块划分;十一进制多目标离散双种群粒子群算法
绿色设计(Green Design)[1-4]让众多企业走出资源能耗大、环境污染严重有了新的希望。在进行产品设计的时候,往往考虑的是多个目标最优的情况,通过考虑一个模型中的参数具有各种不确定性属性的情况下进行问题的分析,本文作者引入了呈随机正态分布的参数模型,目前国内外不乏类似研究[5,6],但同时引入绿色概念、不确定参数、离散多目标多进制粒子群算法最优化求解比较罕见[7-13]。
企业零件库中都有很多零件表供选择,怎样在拥有大量的零件的很多表中分别择优选择一个零件并且成功获得最优的模块划分是个很值得深究的问题。根据模块的特性可知模块具有结构之间的相关性和功能之间的相关性,所属零件之间既有相同的相关性也有自己固有的特点,甚至有随机数的出现来作为模型参数,故不同的零件可能导致不同的模块组合,这是以往很少讨论的。本文针对以上情况,首先研究了模块自身以及模块之间的不确定特性,然后通过一个实体来构建了多目标数学模型,提出一种智能优化算法解决方案,验证了结果的可行性。
1 问题描述
一个轮式装载机部分模块为实例[14],共有11个部件:1.操纵台架、2.驾驶室围板、3.司机椅、4.后视镜、5.前车架、6.后车架、7.铰接、8.挡泥板、9.发动机罩、10.后罩、11.扶梯;分别用T1、T2、T3、T4、T5、T6、T7、T8、T9、T10、T11代表。为了解决该模块组合呈最优状态,同时针对各部件本身也是零件库的情况,每个从零件库中的选择也应该达到最优状态,从而组合配置的轮式装载机最后呈最优。现假设以上部件都是一个零件库,在此我们用数据库表来表示,最终我们就是要从各个零件库中选择一个最优的零件进行最优的组合,组合成的轮式装载机符合我们构建的多目标数学模型最优化。
2 相关介绍
2.1数据表示说明
功能的相关原则是尽量增强模块的功能独立性,让功能比较紧密的单元划分在同一个模块中;结构相关性重在考虑模块结构组合上的相似相关性,以增强其结构的紧密性。这种相关性往往可以依据经验和知识,采用专家分析法来设置。因为这种数据又有一定的模糊不确定性,所以在此我们可以用定量的数来表示,我们可以用“很大”“大”“较大”“一般”“无”来代表功能的相关性值,分别用1,0.8,0.5,0.2,0表示。可以用类似的方法来代表结构的相关程度。零件的属性参数值部分可以参考功能相关性表示方法,其属性也带有随机性,难免随机数的出现,可以采用符合标准正态分布的随机数来表示。
2.2正态分布随机数产生方法
生产出来的产品一般可以让满足正态分布来表示,正态分布随机数的产生有三种方法:
1、利用分布函数的反函数
2、利用林德伯格—莱维(Lindeberg—Levi)中心极限定理
3、使用Box Muller方法
本文统一对随机数采用随机数范围(0,1)之间的标准正态分布,用Box Muller方法获得。
2.3相关性数据和属性值
假设每个零件库表里可供选择的零件都只有两个记录,也就是二选一,同时零部件属性数据值如表1

表1 零部件属性Tab.1 Parts Attribute
各个部件之间的相关性假设值可设置如表2,根据表格的对称性,两部件相关的值只要设置一次就可以,在此鉴于版面问题,我们把该表上三角形一一对应的值来代表功能相关属性值,下三角形一一对应的值来代表结构相关属性值。

表2 相关性值Tab.2 Correlation Value
3 多个目标模型建立[15-17]
3.1模块耦合度和内聚度模型
设某产品由X个基本部件组成,于是部件之间进行组合时候的总关联度为aij=Fω+fij+Sω sij;i,j=1,2…X,Fω和Sω分别代表功能和结构相关属性的权重系数,fij为功能相关属性值,sij为结构相关属性值。假设模块U共有P个基本单元组成,则所有M个模块的总聚合度C1可用式(1)计算:

假设模块U共有P个基本单元组成,模块J共有K个基本单元组成,则可得所有模块间的总耦合度为式(2):
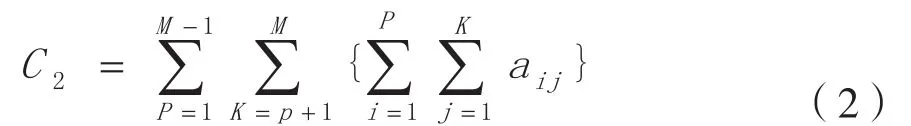
3.2模块绿色度模型
若模块Uh共有Ph个基本单元组成,则它们的对于第k个绿色准则共同的属性值变为,k = 1,2,3,4,5;,k=6,7;这样产品划分为M个模块后的总绿色度为:

式中,kω为第k个绿色准则的权重系数。
4 问题求解
对于式(1),(2),(3)三个目标,将求解满足maxC1,minC2,max协调最优;在计算机领域这属于NP组合问题,常规方法非常耗时,于是提出了一种十一进制多目标离散双种群粒子群算法进行求解。
4.1模型建立
多目标模型的数学表示形式如下:

其中:x为D维决策的向量,y为目标向量,N为优化目标总个数,X是决策向量所获得决策空间,Y是所有目标向量决策形成的决策空间,gi(x)≤0是不等式的约束条件,hj(x)=0是等式约束条件,这些约束条件可以根据情况来设定如何以及有无,它们确定了解的可行范围,和约束了决策向量的搜寻空间以及可行范围。
在求解多目标的数学模型时候,很难找到一个让所有目标都最优的一个解,但是可以想办法找到一个让所有目标尽量最优的一系列解,这样的解就是非劣最优解(pareto解集)。非劣最优解就是不能让某个目标继续最优了,同时也不会让其他的目标变差的情况时候的解。
4.2十一进制多目标离散双种群粒子群算法[19-20]
多个目标要同时达到最优是很难的,只能是各个目标之间协调达到最优,引入Pareto解集,获得非支配解。本文在BPSO(二进制离散基本粒子群算法)基础上提出EHMODDPPSO(Eleven hexadecimal multi-objective discrete double population particle swarm optimization)算法来对问题进行求解。
算法流程如下:
(1)初始化:分别对两个粒子种群进行初始化,十一进制生成十一位编码,比如6,6,6,2,8,8,8,8,9,4,4,相同的数字代表可以归入同一个模块,多少个不同的数字就表示产生了多少个模块划分,
依据此原理生成两个参数各异的粒子种群,他们共享同一个外部精英集。同时产生符合标准正态分布的随机数作为部分绿色属性。
(2)依据Pareto集非支配概念更新粒子外部精英集:更新粒子局部最优向量和粒子全局最优向量(外部精英集),对外部精英解的更新采用非支配方法求Pareto解,如果互不支配时按式(4)对均值排序法求最小的来替代并对相应库表中相应记录数进行刷新,比如1,2,1,1,2,2,2,1,1,1,2,则表示从左到右的库表T1、T2、T3、T4、T5、T6、T7、T8、T9、T10、T11中第几条记录为该表最佳组合选择,表中第一条记录被选用1代表,表中第二条记录被选用2代表。

(3)更新两种群粒子位置:按式(5)(6)刷新各个种群粒子位置向量
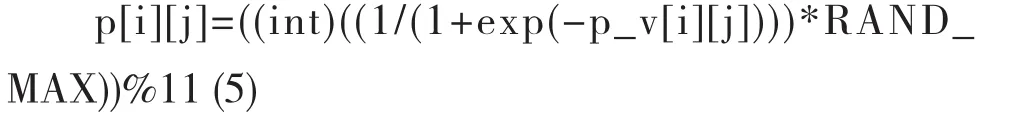
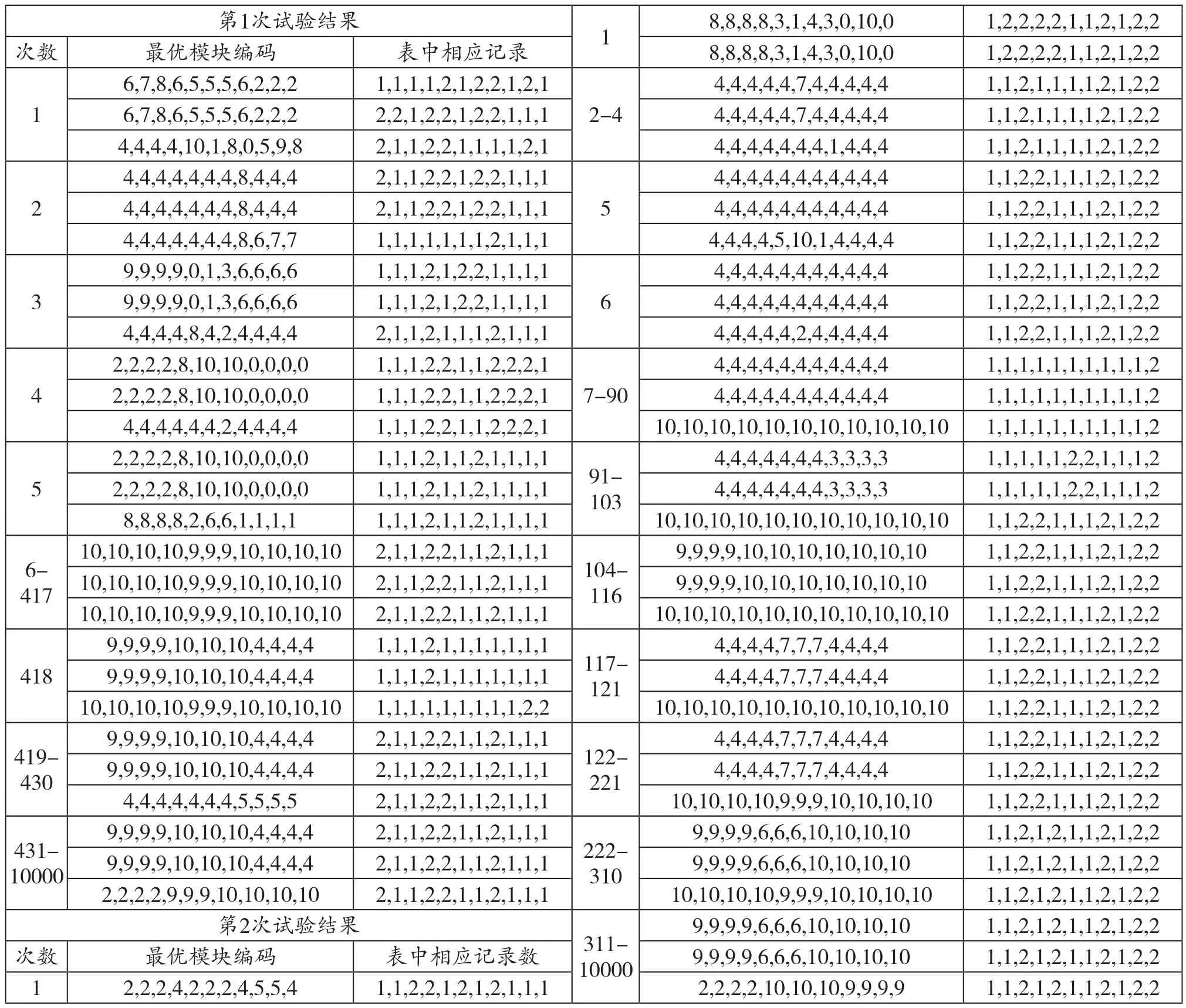
表3 实验结果Tab.3 The Experimental Results
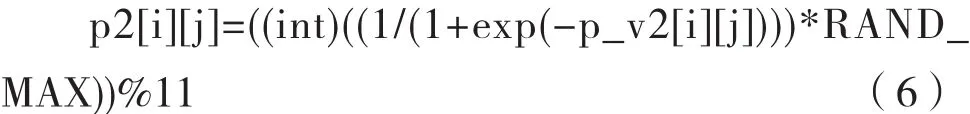
(4)刷新两种群粒子速度向量:按式(7)(8)更新各个种群粒子速度,全局变量靠在三个外部精英集里面随机选择一个来代替。

(5)刷新两种群粒子最优局部向量、外部精英集和零件库表中选择的那个记录数值:按照多目标(1)(2)(3)求解各个种群的非支配集,用当前各自种群的粒子与自身局部向量比较更新局部最优向量和相应库表记录数,依据庄家轮盘法则用当前各自种群的粒子与外部精英集依次比较,非支配或者均值较小的更新留下。相应库表中记录数求解法则:先得到一次粒子编码,在对粒子编码进行分析获知模块个数和对应表的下标,再按式(3)求解。
(6)若达到程序设置迭代最大值就退出,否则继续运行步骤2。
4.3实验
采用C_FREE5.0为运行环境,C语言为脚本语言,设置3个外部精英解,1000个粒子,最大10000次迭代数;同时设置对应的参数权重系数值为w1=w 2=w3=0.3333,w11=w12=0.5;w31=w32=w33=w34=w35 =w36=w37=0.1444。第一个种群学习因子C1=2,学习因子C2=3.5,惯性权重0.5,V_max=8,第二个种群学习因子C1=2.5,学习因子C2=2,惯性权重0.5,V_max=6,实验结果如表3所示。
通过两次实验均获得收敛,而且收敛速度极快;最优模块划分为{操纵台架、驾驶室围板、司机椅、后视镜}为同一模块,{前车架、后车架、铰接}为同一模块,{挡泥板、发动机罩、后罩、扶梯}为同一模块,这也符合文献[14]的结论和实际要求。由于随机数的存在,第一个实验中相应表中记录数为:2,1,1,2,2,1,1,2,1,1,1,即T2、T3、T6、T7、T9、T10、T11表中选第一条记录,T1、T4、T5、T8都选第二条记录;第二个实验中相应的库表中记录数为:1,1,2,1,2,1,1,2,1,2,2,即T1、T2、T4、T6、T7、T9都选第一条记录,T3、T5、T8、T10、T11选第二条记录。两次实验过程中发现零件表中记录数不一样,局部记录数有跳变,但是对于生产当中符合标准正态分布的随机数来说这是正常的。
5 总结
通过一个实体模型,分析了该模型组合中模块本身又是零件库表的情况下,结合本身不确定属性和模块之间的结构相性和功能相关性,引入呈正态分布随机参数,建立符合问题的多目标最优化模型,提出了一种十一进制多目标离散双种群粒子群求解算法,实验结果符合实际要求,实验方法具有合理科学性。随着产品日益丰富的多样性和个性,这种方法的提出能更好的为企业制造业信息化生产带来便利,有一定的生产价值。通过大量的实验发现粒子群算法有其自身的缺陷,比如仍旧容易陷入局部最优,随着零件表中零件数量的增多而收敛速度一般,需要迭代比较多的次数,而且引入随机数的程度在一定程度上影响了每个零件表中记录数的最优选择。作者将继续改进算法,增强粒子扰动,防止提前陷入局部最优,下一步的研究将是利用云计算和大数据相关知识来解决日益增多的零件等复杂性和速度问题。
参考文献(References):
[1] 李秀荣,李中凯,杨建荣 基于混合模块化方法的电梯轿厢模块划分[J]. 机械研究与应用, 2011:47-50
LI Zhongkai, Li Xiurong, Yang Jianrong Based on the hybrid modular approach to the elevator car module division [J]. mechanical research and application 2011:47-50(in Chinese)
[2] 刘光复,刘学平,刘志峰.绿色设计的体系结构及实施策略[J].中国机械工程,2000,11(9):965-968.
LIU Guangfu, LIU Xueping, LIU Zhifeng. The system structure and implementation strategy of green design[J]. China Mechanical Engineering, 2000,11(9):965-968. (in Chinese)
[3] 刘飞,曹华军,何乃军.绿色制造的研究现状与发展趋势[J].中国机械工程,2000,11(1-2):105-110.
LIU Fei, CAO Huajun, HE Naijun. Green manufacturing status and development trend of the research on[J]. Chinese mechanical engineering, 2000,11 (1-2): 105-110. (in Chinese)
[4] 李方义,汪劲松,李剑峰等.产品绿色设计研究现状及展望一般理论及方法[J]. 航空制造技术,2004,29(10):73-78.
LI Fangyi, WANG Jinsong, LI Jianfeng et al. Research status and Prospect of product green design and general theory and methods [J]. aeronautical manufacturing technology, 2004,29 (10): 73-78. (in Chinese)
[5] 郭文忠,陈国龙. 一种求解多目标最小生成树问题的有效离散粒子群优化算法[J].模式识别与人工智能2009,22(4): 598-602
GUO Wenzhong, CHEN Guolong,A multi-objective minimum spanning tree problem of discrete particle swarm optimization algorithm[J]. pattern recognition and artificial intelligence, 2009,22 (4): 598-602(in Chinese)
[6] 张莉, 彭文敏. 求解多目标TSP问题的离散粒子群优化算法[J]. 中国高新技术企业, 2010,(3): 28-30.
ZHANG Li, PENG Wenmin. A discrete particle swarm optimization algorithm for solving multi objective TSP problem[J]. China high tech enterprise in 2010,(3):28-30. (in Chinese)
[7] 陆长明, 陈峰, 邓劲莲. 绿色性对模块化产品设计的影响[J]. 机械设计与研究,2006,22(6):13-16.
LU Changming, CHEN Feng, Deng Jinlian. Effects of green property on modular product design[J]. mechanical design and research, 2006,22 (6): 13-16. (in Chinese)
[8] 李婷婷, 龚京忠, 李国喜等. 可维修性驱动的模块划分[J].机械设计与制造.2007,45(02):166-168.
LI Tingting, GONG Jingzhong, LI Guoxi et al. Maintainability drive modules of[J]. mechanical design and manufacture. 2007, 45 (02): 166-168. (in Chinese)
[9] Tseng HE, Chang CC, Li JD.Modular design to support green life-cycle engineering[J]. Expert Systems with Applications,2008,34(4):2524-2537.
[10] 郭卫,刘光复,张雷.面向全生命周期的产品绿色模块划分方法研究[J]. 合肥工业大学学报(自然科学版).2010,33(10):1441-1445,1449.
GUO Wei, LIU Guangfu, ZHANG Lei. Study on the division method of product green modules in the whole life cycle[J]. Journal of HeFei University of Technology (Natural Science Edition)2010,33(10): 1441-1445,1449. (in Chinese)
[11] Smith S, Yen CC. Green product design through product modularization using atomic theory[J]. Robotics and Comp uterIntegratedManufacturing,2010,26(6):790-798.
[12] 陈小斌. 机电产品绿色模块划分方法研究与应用[D]. 杭州: 浙江大学,2012.
CHEN Xiaobin. Research and application of green module partition method for mechanical and electrical products[D]. Hangzhou: Zhejiang University, 2012(in Chinese)
[13] Ji Y J, Jiao RJ, Chen L, Wu C L. Green modular design for material efficiency: a leader-follower joint optimization model[J]. Journal of Cleaner Production, 2013, 41(2):187-201.
[14] 胡君君,基于模块化的装载机工作装置变型设计方法研究[D]. 柳州:广西工学院,2011
HU Junjun. Research on the variant design method of working device of Loader Based on modularization[D]. Liuzhou: Guangxi University of Technology, 2011(in Chinese)
[15] 刘电霆.绿色设计中产品模块划分的不确定优化及GA求解[J]. 桂林理工大学学报,2013,33(4):743-748.
LIU Dianting. Green design module partition in uncertain optimization and genetic algorithm [J]. Guilin University of technology, 2013,33 (4) 743-748. (in Chinese)
[16] Vilfredo Pareto. CoursD'EconomiePolitique[M]. volume I and II. F. Rouge, Lansanne, 1896
[17] 唐涛,刘志峰,刘光复等. 绿色模块设计方法研究[J]. 机械工程学报,2003,39(11):149-154.
TANG Tao, LIU Zhifeng, LIU Guangfu et al. Study on the design method of green module[J]. Journal of mechanical engineering, 2003,39 (11): 149-154. (in Chinese)
[18] 宋武. 解决多目标优化问题的粒子群算法研究[D]. 湘潭:湘潭大学,2007.
SONG Wu. A particle swarm optimization algorithm for solving multi objective optimization problems [D]. Xiangtan: Xiangtan University, 2007(in Chinese)
[19] 贾庭芳, 基于粒子群优化的离散多目标优化算法[D]. 太原:太原科技大学,2011.
JIA Tingfang. Discrete multi objective optimization algorithm based on particle swarm optimization[D]. Taiyuan: Taiyuan University of Science and Technology,2011. (in Chinese)
[20] 唐文献, 吴春艳, 马宝等. 基于模糊聚类分析的锚绞机模块划分方法研究[J]. 机械设计, 2012,29(10):24-28.
TANG Wenxian, WU Chunyan, MA Bao et al. Based on the fuzzy clustering analysis of the anchor winch module partition method[J]. Mechanical design, 2012,29 (10): 24-28.(in Chinese)
【责任编辑:高潮】
【信息技术理论研究】
The optimization method of green module of EHMODDPPSO based on uncertain
HU Haoping
(School of Finance and Economics, Shenzhen institute of information technology, Shenzhen, 518172, China)
Abstract:Study on the parts of the attribute is standard normal distribution random number problems of uncertainty,considering the green attributes of the part module between functional correlation and structure correlation and parts library itself, the uncertainty optimization model of product green module contains the cohesion, coupling degree,green degree three objective functions of the division, the proposed EHMODDPPSO method, to find the optimal module partition and the optimal corresponding parts list parts. With a wheel loader module as an example, to verify its rationality and feasibility.
Keywords:uncertain optimization; random number; module; eleven hexadecimal multi-objective discrete double population particle swarm optimization algorithm
中图分类号:TH122; TP301.6; O224
文献标识码:A
文章编号:1672-6332(2016)01-0017-07
[收稿日期]2016-01-15
[作者简介]胡浩平(1981-),男(汉),湖南汨罗人,硕士,讲师,主要研究方向:智能计算,制造业信息化。E-mail:1628619275@qq.com

