轨道车辆垂向振动的Matlab建模与仿真教学研究

洪 磊 赵素芳 聂丽青南京工程学院汽车与轨道交通学院 江苏南京 211167



轨道车辆垂向振动的Matlab建模与仿真教学研究

洪 磊 赵素芳 聂丽青
南京工程学院汽车与轨道交通学院 江苏南京 211167

摘 要：在城市轨道车辆工程课程的教学中，城轨车辆垂向振动问题的分析需建立并求解复杂的微分方程，给学生理解带来较大困难，应用Matlab的可视化仿真工具Simulink建立二系簧车轮荷重系统垂向振动的仿真模型，在此基础上对车体和转向架的垂向自由振动规律进行了较详细的仿真分析。结果表明，仿真结果与理论分析方法具有一致性，验证了Matlab仿真方法在城轨车辆垂向振动教学中具有较好的应用价值。

关键词：轨道车辆；垂向振动；Matlab/Simulink；二系簧；车轮荷重系统

随着我国城市轨道交通的不断兴建，社会对城市轨道交通车辆专业人才的需求也在不断增加。近年来，南京工程学院以培养高素质工程技术应用型人才为导向，在车辆工程学科下开设了城市轨道车辆专业，教学内容紧密结合城市轨道车辆产业现状，形成了具有一定特色的专业发展方向。城市轨道车辆工程课程是城市轨道车辆专业方向的一门专业必修课，开设于大三上学期，教学目标是使学生掌握城市轨道车辆的基本特征、结构原理和总体设计方法，为学生学习本专业后续课程打下基础。由于该课程贴合实际，因而学生在学习中表现出浓厚的兴趣。然而，学生普遍反映该课程中数学推导公式较多，而教材的分析过程过于抽象，理解困难，其中尤以城轨车辆垂向振动分析一章为最。

城轨车辆的垂向振动分析是城市轨道车辆工程课程教学的一个重点[1]，然而城轨车辆垂向振动问题的分析需建立并求解复杂的微分方程，给教学带来了诸多不便。教学中涉及微分方程的解算，不仅枯燥且耗费大量的时间，其结果的分析较为抽象，学生理解也比较困难，因此，形象直观地进行教学，激发学生的学习兴趣和学习的主动性，提高教学质量，将计算机仿真技术引入教学中是一种比较理想的方法。以二系簧车轮荷重系统的垂向振动规律为教学研究对象，应用Matlab的可视化仿真工具Simulink建立二系簧车轮荷重系统的仿真模型，并且对仿真结果进行分析，使学生更易于理解和掌握。

1 Matlab/Simulink简介

Matlab/Simulink是由美国Mathworks公司推出的基于框图的动态系统建模与仿真平台，Simulink是Matlab最重要的组件之一，它以Matlab的强大计算功能为基础，以直观的模块框图进行仿真和计算[2]。Simulink提供了各种仿真工具，尤其是其内容丰富的模块库，为复杂系统的构造与仿真分析带来了极大的便利。在Simulink环境下可利用基本模块库和数学模块库对城轨车辆振动系统进行仿真[3,4]，从而为振动规律的教学和研究提供强有力的仿真环境。

2 二系簧车轮荷重系统的垂向振动仿真

为了揭示城轨车辆垂向振动的规律，可以将整个城轨车辆系统简化为由若干质量和弹簧减振元件等组成、由无质量的轮对(或车轮)支承着沿轨道运行的振动系统，即车轮荷重系统[1]。其中，只有2个质量(车体和转向架)和2个弹簧减振元件(一系弹簧和二系弹簧)构成的振动模型称为二系簧车轮荷重系统，它的振动形态能在很大程度上反映城轨车辆振动的一般性规律。对二系簧问题的深入讲解，既便于学生入门和理解，也为后续整个车辆系统振动规律的教学奠定了基础。

2.1 二系簧车轮荷重系统动力学模型

轨道车辆二系簧车轮荷重系统垂向振动的动力学模型如图1所示，该模型用一个无质量的轮对代表城轨车辆各轮对在轨道上的运行特点，转向架和车体各简化为一个质量块，转向架和车体的总质量分别为M1和M2。轮对与转向架之间、转向架与车体之间分别简化为一系弹簧和二系弹簧，一系与二系弹簧的刚度分别为k1和k2，本文着重讨论转向架与车体的固有振动特性，故模型不考虑减振元件。

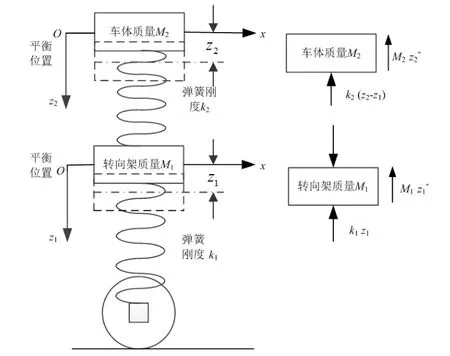
图1 二系簧车轮荷重系统垂向动力学模型

在图1中，z1和z2分别表示转向架和车体偏离各自平衡位置的位移，z1′′和z2′′分别为各自的运动加速度。根据牛顿第二定律，可以得到车体与转向架的运动方程分别为：

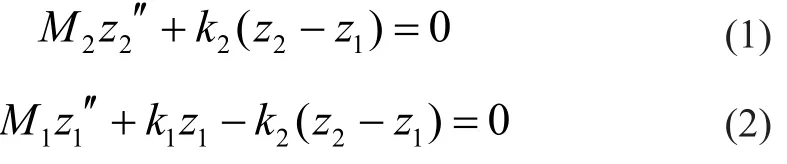
由式(1)和(2)可得系统特征方程为：

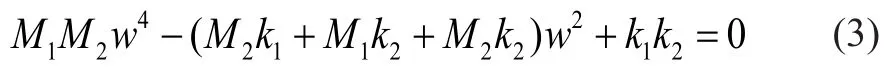
对特征方程进行求解，可以得到两个特征解：

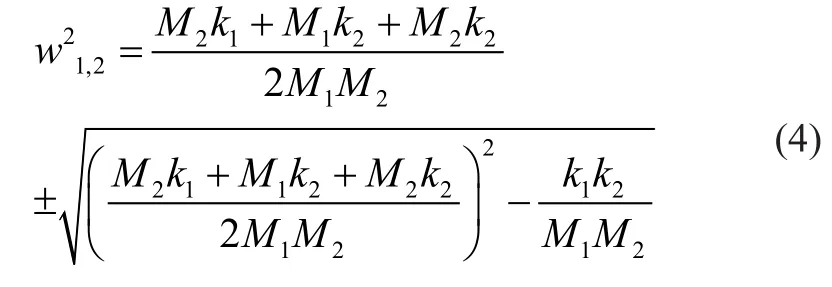
式中，w1和w2分别表示系统的低频振动频率和高频振动的频率。

设第1系弹簧的静挠度为f1，第2系弹簧的静挠度为f2，这两系弹簧总的静挠度为f。由于车体质量M2远远大于转向架质量M1，故可近似得到：

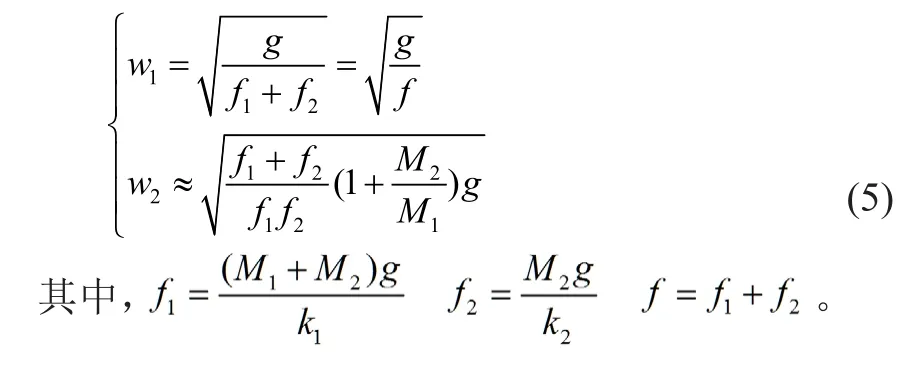
车体和转向架在垂直方向上的沉浮自由振动形式均是由低频振动、高频振动这两种振动形式所组成的，所以，它们的沉浮自由振动也是由高低两种不同的振动频率的振动形式所叠加而成，有：

式中，A1,A2分别表示转向架垂向自由振动低频振动波和高频振动波的振幅；B1,B2分别表示车体垂向自由振动低频振动波和高频振动波的振幅。

转向架和车体之间的振幅比分别为A1/B1和A2/B2，两者都是常数，是由系统原本参数来确定的，与系统振幅的绝对值没有关系。

2.2 Simulink仿真模型

2.1节通过理论分析方法得出了轨道车辆二系簧车轮荷重系统垂向振动的一般规律，给出了车体和转向架运动方程、系统二阶固有频率、振动形式和振幅比特性的理论描述。但上述分析涉及微积分和线性代数理论，解算过程复杂，特别是振幅比特性描述更为抽象，给学生的理解造成很大困难，为此，由系统运动方程式(1)和(2)出发,利用Matlab/ Simulink建立二系簧车轮荷重系统的垂向振动的仿真模型，如图2所示，示波器Scope1和2分别显示转向架和车体振动位移波形，由此可直观地对系统振动特性进行分析。

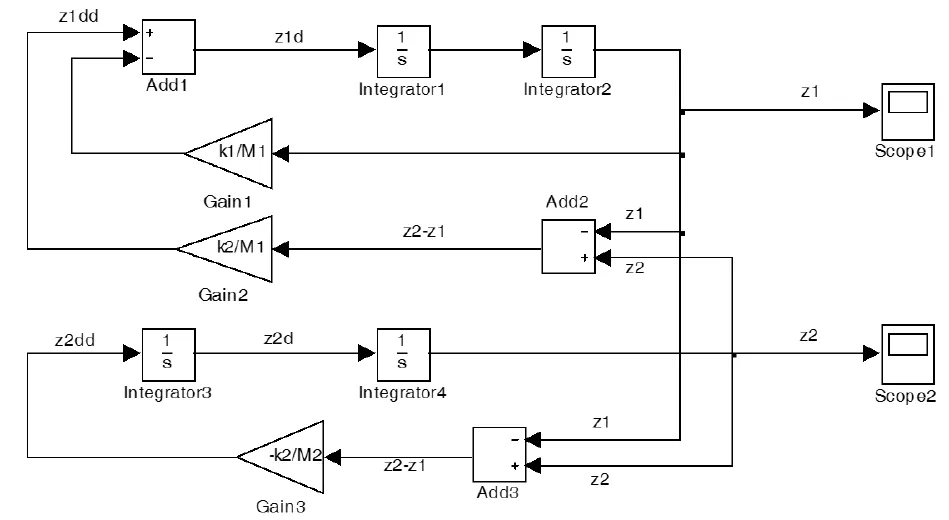
图2 二系簧车轮荷重系统垂向振动Simulink仿真模型

2.3 参数设置与仿真分析

根据我国铁路客车运行的实际情况[5,6]，在图2振动仿真模型中，设置各项参数如下：转向架质量M1=4.5t ，车体质量M2=45t，两系弹簧总的静挠度为f =170mm，取第2系弹簧悬挂和第1系弹簧悬挂两者静挠度的比值为f2/ f1=64/36，由此算得第一系弹簧和第二系弹簧的静挠度分别为f1=61.2mm 、f2=108.8mm ，进一步算得k1=7.935× 103N/ mm ，k2=4.057× 103N/ mm 。由公式(5)可算得系统的固有频率分别为w1=7.59rad/s,w2=52.49rad/s。

将系统仿真的时间设为2s，仿真步长设为0.02。设转向架与车体初始速度和加速度均为0。并按如下三种方式设置位移初始条件，分别为：

(a)转向架z1= 30 mm ，车体z2=− 1.5 mm ；

(b)转向架z1= 20 mm ，车体z2=− 1 mm ；

(c)转向架z1=− 10 mm ，车体z2= 0.5 mm 。

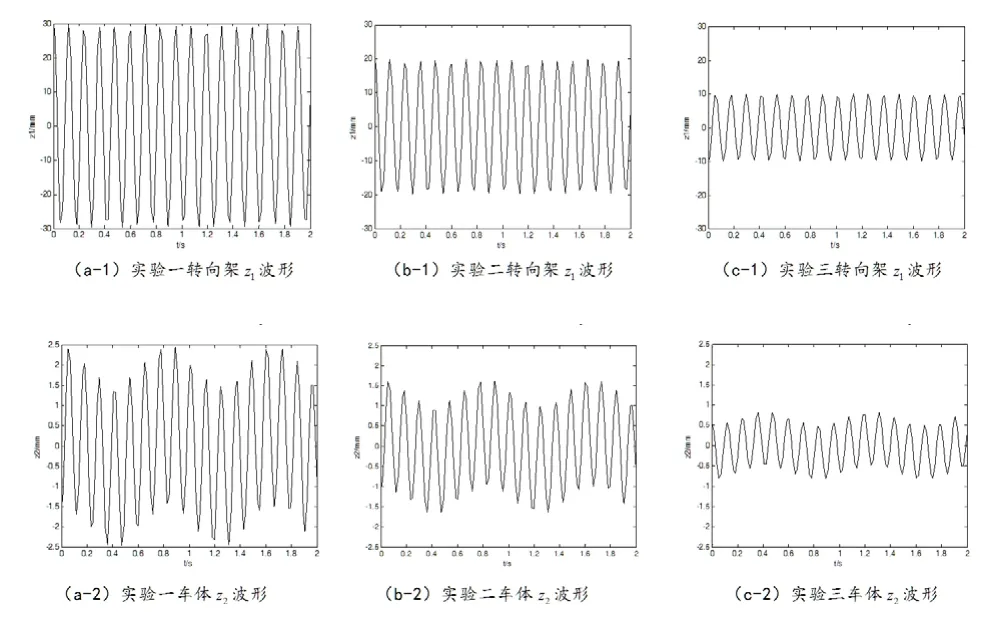
图3 转向架与车体三组仿真实验垂向振动位移波形图

三种初始条件下的转向架与车体振动波形图如图3所示，将上述波形对应的数据分别导入Matlab的cftool拟合工具箱进行曲线拟合[7]，拟合曲线类型设为式(6)所示的正弦函数和形式，拟合方法采用默认的Trust-Region算法[8]，由此可得到三组仿真实验的拟合结果，见表1。

根据表1的拟合结果，可以得出如下分析结论：

(1)转向架和车体的振动由低频和高频两种振型组成，固有振动频率相同且不受初始条件影响，低频频率w1=7.557 rad/s，高频频率w2=52.77 rad/s，与理论计算结果基本相同。

(2)转向架和车体之间的振幅比近似为常数，与系统振幅无关，三组实验的结果非常接近，求其均值可得本系统的低频振幅比为0.6765，高频振幅比为14.7876，与理论分析相符。

(3)由相位关系可见，低频振动时转向架和车体的位移方向相同，高频振动时转向架和车体的位移方向相反，且不随初始条件而改变，这也与理论分析结果相一致。

3 结束语

在城市轨道车辆工程课程的教学过程中，为了深入讲解车体和转向架的垂向振动分析问题，应用Matlab/Simulink建立了二系簧车轮荷重系统的垂向振动仿真模型，通过波形显示和拟合分析，使学生直观快捷地理解了轨道车辆二系簧系统的固有振动规律。经过教学实践得出如下几点体会：第一， Malab/ Simulink突破了微分方程推导和求解的困难，仿真框图简单直观，其结果与理论分析结论完全相符，提高了课程教学的生动性，增强了学生的学习兴趣；第二，让学生掌握了Matlab/Simulink仿真工具的使用，认识到它在实际应用中的作用，有利于举一反三，进一步应用于课程其他内容的分析；第三，专业知识和软件技术的结合，很大程度上提高了教师和学生的综合专业能力。综上所述，Matlab/Simulink作为现代教育技术的一种手段具有较好的推广价值。

参考文献

[1] 王伯铭.城市轨道交通车辆工程[M].成都:西南交通大学出版社,2007.

[2] 宋志安.Matlab/Simulink与机电控制系统仿真[M].北京:国防工业出版社,2011.

[3] 颜秋,刘永明.基于Matlab/Simulink的车辆建模与故障分析[J].华东交通大学学报,2012,29(5):13-17.

[4] 张剑,沈钢. 惯容悬挂元件对铁路车辆垂向振动的影响[J].华东交通大学学报,2014,31(4):11-15.

[5] 严隽耄,傅茂海.车辆工程[M].第三版.北京:中国铁道出版社,2009.

[6] 陆冠东.车辆系统动力学计算方法研究[M].北京:中国铁道出版社,2012.

[7] 陈岚峰,杨静瑜,崔崧.基于Matlab的最小二乘曲线拟合仿真研究[J].沈阳师范大学学报:自然科学版,2014,32(1):75-79.

[8] 王国强.机械优化设计[M].北京:机械工业出版社,2009.

The Teaching Research on Matlab Modeling and Simulation of Vertical Vibration for Rail Vehicle

Hong Lei, Zhao Sufang, Nie Liqing
School of Automotive and Rail Transit, Nanjing Institute of Technology, Nanjing, 211167, China

Abstract:In the course of urban rail vehicle engineering teaching, it is needed to establish and resolve complex differential equation to analysis on urban rail vehicle vertical vibration, which brings much difficulties to students’ understanding, In this paper, it is used of Matlab and its visualization and simulation tools Simulink to establish the wheel load system simulation model with two series springs, and the vertical vibration rules of rail vehicle body and bogie are carried out on the basis of the detailed simulation analysis. The results show that the simulation waveforms are consistent with the results of the theoretical analysis method, verify that the Matlab simulation method has good application value on teaching of urban rail vehicle engineering.

Key words:rail vehicle; vertical vibration; Matlab/Simulink; two series springs; wheel load system

收稿日期：2015-10-23

作者简介：洪磊 ，博士，讲师。

基金项目：南京工程学院科研基金项目“城市轨道车辆重要部件安全性分析与故障诊断”(编号：YKJ201333)。