老树发新芽 古琴生新韵
——例谈利用平面向量基本定理解决相交平面的交线问题
罗风云 马 杰
(安徽省宿州学院附属实验中学,234000)
老树发新芽古琴生新韵
——例谈利用平面向量基本定理解决相交平面的交线问题
罗风云马杰
(安徽省宿州学院附属实验中学,234000)
前一阶段,笔者在进行高三立体几何的复习时,讲解了这样一道题:
题目如图1所示,在正方体ABCD-A1B1C1D1中,E、F分别为棱AB、CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线()
(A)不存在(B)有1条
(C)有2条(D)有无数条
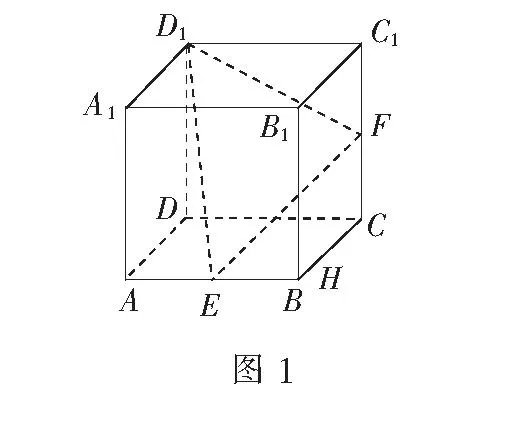
分析平面ADD1A1与平面D1EF有公共点D1,则必有过该点的公共直线l,在平面ADD1A1内与直线l平行的线有无数条,且它们都不在平面D1EF内,由线面平行的判定定理知它们都与平面D1EF平行,故选D.

在解答完此题之后,学生提出这样一个问题:既然平面ADD1A1与平面D1EF有交线,那么交线在哪?如何作出来?为此,笔者给出一个传统解法:首先,平面ADD1A1与平面D1EF有公共点D1,因此,交线一定过点D1. 如图2所示,延长D1F交DC的延长线于点G,连结EG交BC于点H,交DA的延长线于点I,连结D1I,则平面ADD1A1与平面D1EF的交线为D1I.
学生对此解法提出:此种解法需要作辅助线,能否有不需要作辅助线的通用解法?此时,笔者想到,既然我们学习了向量法来解决立体几何问题,那么能否用它来解决?因为交线分布在两个不同平面,因此,交线所在向量就可以分别利用这两个平面内的基底表示,于是借助平面向量基本定理尝试了如下的探索.
如图3所示,以DA为x轴、DC为y轴、DD1为z轴建立空间直角坐标系,不妨设正方体ABCD-A1B1C1D1的边长为1,所求两平面的交线所在的方向向量为m.

首先,两平面交线在平面ADD1A1与平面D1EFK中,故可设


即m=λ1(1,0,0)+λ2(0,0,1)
=(λ1,0,λ2),


由此可得
不妨设方向向量m的始点为顶点D1,终点为点I(x,y,z),则

由平面向量基本定理,可知取λ2=-1,通过方程组可求得

从以上过程可以看出,使用平面向量基本定理来解决交线问题,不仅回避了作辅助线这个难点,而且可以精确定位交线的位置,一举两得.下面介绍这种方法在多面体截面问题中的应用.
例1(第十四届希望杯全国数学邀请赛)一平面与正方体表面的交线围成的封闭图形称为正方体的“截平面图形”. 棱长为1的正方体ABCD-A1B1C1D1中,E是AB的中点,F是CC1的中点, 则过D1,E,F三点的截平面图形的周长等于()





评注此法不仅可以确定截面图形的形状,还可通过截面顶点坐标求出周长.
例2(第16 届美国数学邀请赛)如图5所示,正方体的三条棱为AB、BC、CD,AD是体对角线. 点P、Q、R分别在AB、BC、CD上,AP=5,PB=15,BQ=15,CR=10, 那么, 平面PQR向各方向延展后与正方体的交线组成的多边形的面积是多少?

解依题意,正方体的边长为20,如图6所示,建立空间直角坐标系,则相关各点的坐标分别是O(0,0,0),C(0,20,0),F(0,0,20),P(20,5,0),Q(5,20,0),R(0,20,10).不妨设所求平面PQR与平面OCDF的交线所在的方向向量为m,故可设

即m=λ1(0,-20,0)+λ2(0,0,20)
=(0,-20λ1,20λ2).


即m=λ3(-15,15,0)+λ4(-5,0,10)
=(-15λ3-5λ4,15λ3,10λ4).
因此,(0,-20λ1,20λ2)=(-15λ3-5λ4,15λ3,10λ4),由此可得
不妨设方向向量m始点为顶点R,终点为点S(x,y,z),则


以此类推,找到截面图形为六边形PQRSTU,坐标如下:P(20,5,0),Q(5,20,0),R(0,20,10),S(0,15,20),T(15,0,-20),U(20,0,10),因此所求的截面图形的面积
SPQRSTU=2SPQRU=2(S∆PQR+S∆PRU)=
=525.

利用平面向量基本定理求解上述问题的实质是将几何图形的相互位置的确定转化为向量的代数运算,体现了“数与形”的有效结合,淡化了立几问题传统方法“由形到形”的推理,不但为学生提供了一个崭新的视角,丰富了其思维结构,而且为学生增强了可操作性,消除了学生对此类问题的障碍.在高三复习备考中,有必要把向量与其他知识内容进行有效整合,使向量成为解决数学问题一种重要的工具, 从而探索出新的解题途径. 在日常教学中,教师要引导学生多角度思考问题,积极培养学生的创新能力与发散思维,只有这样才能使得学生在解题能力上获得质的提高.
○解题思路与方法○

