基于具有同时选择的动态博弈模型的最优关税选择

吴宇溦

(江西财经大学 会计学院，江西 南昌 330013)

基于具有同时选择的动态博弈模型的最优关税选择

吴宇溦

(江西财经大学 会计学院，江西 南昌 330013)

摘要：随着各国经济贸易日益加深，关税的选择对于两国的外贸尤为重要。将有同时选择的动态博弈模型，应用到两国之间的最优关税选择问题上，得到两国之间最优关税、最佳内销产量和最佳出口产量，并且受到两国企业某产品的边际生产成本与初始需求量的影响。

关键词:同时选择；动态博弈模型；最优关税

随着各国政府不断地加大对外开放的程度，各国之间的贸易往来也越加频繁，政府的关税选择将直接影响到两国之间的贸易，为此关税的选择对外贸具有深远的影响。关税选择的模型上大都借鉴了博弈论的思想，从最早的古诺模型、斯坦伯格模型到现在的一般均衡模型，都无一例外地传承了博弈的思想。此外，还有一些学者从不同角度探讨了关税选择的模型。聂规划等(2006)在国际战略贸易理论基础上，采用三阶段动态博弈模型来分析关税对三国之间贸易的影响；赵驰等(2007)从寻租这个角度分析了关税税率的选择对社会福利以及对外贸易的影响；刘海云等(2007)将中间产品引入到“保护待售”模型中对关税的结构进行政治性因素分析。这些学者关于关税选择的研究，都具有一定合理性，但是需要注意的是，关税的选择还需要考虑贸易双方的具有相同的地位，都会根据对方的决策选择关税的制定。因此，本文将依据关税制定的特点，利用有同时选择的动态博弈模型来对两国之间的关税进行最优选择。

1有同时选择的动态博弈模型

有同时选择的动态博弈模型研究的是在同一阶段有两个或两个以上决策者同时选择的情况博弈，它的特点在于博弈双方所处的博弈环境并非是完美信息环境，而是介于完美信息与非完美信息之间。但是，值得注意的是，这种博弈却有着与完美信息动态博弈相同特征，并且解法也相一致。本文只是讨论了在两个阶段下两个不同决策者同时选择的动态博弈；类似地，如果有更多阶段或者更多决策者可以通过简单推广。不失一般性，我们对博弈进行以下假设。

(1)有四个决策者： i=1,2,3,4。

(2)决策者1与决策者2在第一阶段在各自的可选策略集合A1和A2中分别选择a1和a2。

(3)决策者3与决策者4在了解第一阶段决策者1和决策者2作出的策略(a1,a2)后，在第二阶段中，在各自的可选策略集合A3和A4中分别选择a3和a4。

(4)决策者选择特定的策略a1,a2,a3和a4就有唯一的收益与之对应，即决策者i的收益 ui(a1,a2,a3,a4)，是决策者策略的函数。

类似于完美信息动态博弈的解法，这种有同时选择的动态博弈问题的方法一般采用的是逆推归纳法。不过，这种动态博弈在第二阶段(即最后一个阶段)的求法并不再像一般动态博弈那样只求单方利益最大化，而是一个在决策者3、4之间的博弈，并且由于该博弈过程的差异化，使得传统的子博弈的概念也要做出相应地变化。事实上，两个决策者在这个阶段博弈，双方都具有同时选择的机会，类似于一个静态博弈。经过上述的假设和定义，例如子博弈完美纳什均衡等概念就可以在后文的分析中运用。

2最优关税模型

鉴于两国之间的关税博弈的特点，本文将引进有同时选择的动态博弈模型对其研究，并给出最优的关税选择。在此我们以简单的两个相似的国家为例进行分析，分别设为国家1和国家2，鉴于两国贸易之间往来所能产生博弈的机制，本文选取关税税率作为双方博弈的决策变量。为了方便下文分析，我们假设将两个国家所在的国内所有企业集合起来作为一个综合企业，并且该企业生产的产品既可以在本国销售也可以出口在另一个国家销售，两个国家的消费者在各自国家都可以对本国内销的产品以及另一个国家进口的产品进行选择消费。

接下来，开始对两国之间的关税最优选择模型进行设定。首先假定国家1和国家2同时制定关税率为 t1和t2；然后企业1和企业2为了利润最大化原则根据各国设定的关税率t1和 t2同时决定各自的内销和出口产量 (h1,e1)和(h2,e2) 。 此时，最优关税的选择就是一个两阶段决策者都有同时选择的动态博弈，并且根据经济利润理论易得第 i国企业的利润函数为：

πi=πi(ti,tj,hi,hj,ei,ej)=Pihi+Pjei-c(hi+ei)-tjei

=[a-(hi+ej)]hi+[a-(hj+ei)]ei-c(hi+ei)-tjei

值得注意的是，在决策中，决策者不仅仅只在乎经济利润的最大化，还会关心整个国家的社会总福利。本国企业的总利润只不过是社会总福利的一个部分，本文还将消费者剩余和关税收入算入到社会总福利中。西方经济学认为消费者剩余表示消费者通过消费使得自身福利的改善，它用来衡量消费者购买产品后所获得的额外利益，以消费者愿意支付的最高价格与这些商品的实际市场价格来计算，又因为本文假定需求曲线是线性的，所以消费者剩余为：

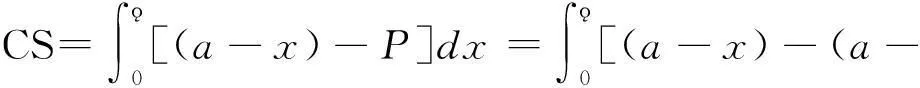
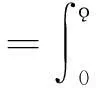
因此，第 i国政府的福利函数为

式子中 i=1,2，加法各项分别代表国家 i国内居民作为消费者的消费者剩余、企业利润和关税收入。

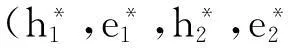
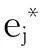
企业在国内市场下要达到利润最大化，那么内销产量 hi必须满足：

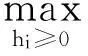
企业在国外市场下要达到利润最大化，那么出口产量ei必须满足：

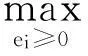
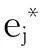
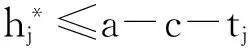
又因为在上述分析中并未对特定的国家的特定的企业进行设定，因此式子(3)、(4)对 i=1,2都是成立的。于是，可以得到四个方程组成的联立方程组，并将其求解得：

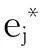
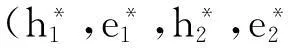
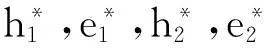
又由于在第二阶段的最优解带入到第 i国政府的福利函数中可得：

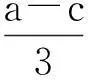
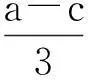
3结论

本文首先介绍了具有同时选择的动态博弈模型，并依据两国之间的关税制定的特点，利用该模型来确定两国之间的最优关税的确定。最后得出两国企业某产品的边际生产成本与该产品的初始需求量会影响关税率、最佳内销产量和最佳出口产量，分别为 (a-c)/3、4(a-c)/9和 (a-c)/9。此外，这个动态博弈的最优解是一个子博弈完美纳什均衡解。

参考文献：

[1]聂规划,贺铸.贸易关税的博弈模型[J].统计与决策,2006(06):61-62.

[2]赵驰,陈志丹.权力寻租现象的再解释-基于关税的理论视角[J].统计与决策,2007(20):111-113.

[3]刘海云,吴韧强.关税结构的政治经济学解释-基于“保护待售”模型的博弈分析[J].经济学(季刊),2007,7(1):345-358.

[4]张维迎.博弈论与信息经济学[M].上海:上海人民出版社,2012.

[5]朱顺泉.经济博弈论及其应用[M].北京:清华大学出版社,2013.

[责任编辑：吴祝平]

The Optimal Tariff Choice in a Dynamic Game Model with Simultaneous Selection

Wu Yuwei

(JiangxiUniversityofFinanceandEconomics,Nanchang330013Jiangxi)

Abstract:With the deepening of national economic and trade,the choice of tariff is particularly important for the trade between the two countries.Applying the dynamic game model with simultaneous selection into the problem of choosing the optimal tariffs between two countries in order to get the optimal tariffs,the best domestic production and the best export yield between two countries was influenced by the marginal cost of production and the initial demand quantity of a certain product in two countries.

Key words:Simultaneous selection; Dynamic game model; Optimal tariff

* 收稿日期：2016-05-14

基金项目：江西财经大学研究生创新项目(2015SYK036)。

作者简介：吴宇溦，女，福建南平人，硕士研究生。研究方向：公司估值与企业博弈。

中图分类号：F745.5

文献标识码：A

文章编号：1672-1047(2016)03-0079-04

DOI：10.3969/j.issn.1672-1047.2016.03.22