关于丢番图方程1+2x11y+5z11u=2v5w，xvw>0，y+u>0

陈小燕

(琼台师范高等专科学校 数理系，海南 海口　571100)

关于丢番图方程1+2x11y+5z11u=2v5w，xvw>0，y+u>0

陈小燕

(琼台师范高等专科学校 数理系，海南 海口571100)

摘要：讨论了丢番图方程1+X+Y=Z 的一个特殊情形。借助计算机，用初等方法给出了指数丢番图方程1+2x11y+5z11u=2v5w，xvw>0，y+u>0的全部非负整数解。

关键词：指数丢番图方程；非负整数解；同余解；计算机辅助解法

0引言

设x，y，z，u，v，w为非负整数，考虑指数丢番图方程

1+2x11y+5z11u=2v5w，xvw>0，y+u>0。

(1)

显然，方程(1)是丢番图方程

(2)

表1　方程(1)的同余解

(b)方程(1)的同余解但不满足

(c) 方程(1)的同余解但不是方程(1)的解

的一种特殊情况，这里p1，p2，…，pt是素数，S是给定的有限集。方程(2)的解可用于有限群的分类[1]。例如：曹珍富[2]定出了阶为2α13α25α37α4pα5的单群。虽然形如(2)的某些具体方程不借助计算机也可以求解[3]，但是借助计算机则计算时间将大大减少。如：Alex L J和Foster L L[4]借助计算机用初等方法给出方程1+x+y=z，xyz=2r3s7t的所有非负整数解。文[5-10]用计算机辅助解法分别给出了指数丢番图方程2x+2y+3z11u=3v11w与px-qy=2等的全部非负整数解。在本文中，借助计算机，用初等方法给出了(1)的所有非负整数解。

1引理

引理1设(x，y，z，u，v，w)是方程(1)的任一解，(x，y，z，u，v，w)≡(a，b，c，d，e，f)(mod60，120，60，120，60，60)。则满足1≤a，e，f≤60， 0≤c≤59， 0≤b，d≤119的所有(a，b，c，d，e，f)(称为(1)的同余解)由表1给出。

证明设(x，y，z，u，v，w)是方程的解，由于

260≡1(mod52·7·9·11·13·31·41·61)

5060≡1(mod24·7·9·11·13·31·41·61)

11120≡1(mod25·52·7·9·13·31·41·61)，

设(x，y，z，u，v，w)≡(a，b，c，d，e，f)(mod60，120，60，120，60，60)，1≤a，e，f≤60，0≤c≤59，0≤b，d≤119，则应有1+2x11y+5z11u≡2v·5w(mod7·9·13·31·41·61)。

令s=min(a，e，4)，t=min(c，f，2)，则有

1+2x11y+5z11u≡2v·5w(mod2s·5t·7·9·13·31·41·61)

(3)

本文编写了简单的UBASIC程序，在1≤a，e，f≤60， 0≤c≤59， 0≤b，d≤119的范围内对(3)进行检验，得到(a，b，c，d，e，f)由表1(a)和表1(b)给出。

说明：UBASIC可以表示-65536542～65536542的整数，因而(3)及后面相关的同余式可以方便地在计算机上检验。

2定理

定理1丢番图方程

1+2x11y+5z11u=2v5w，xvw>0，y+u>0　(4)

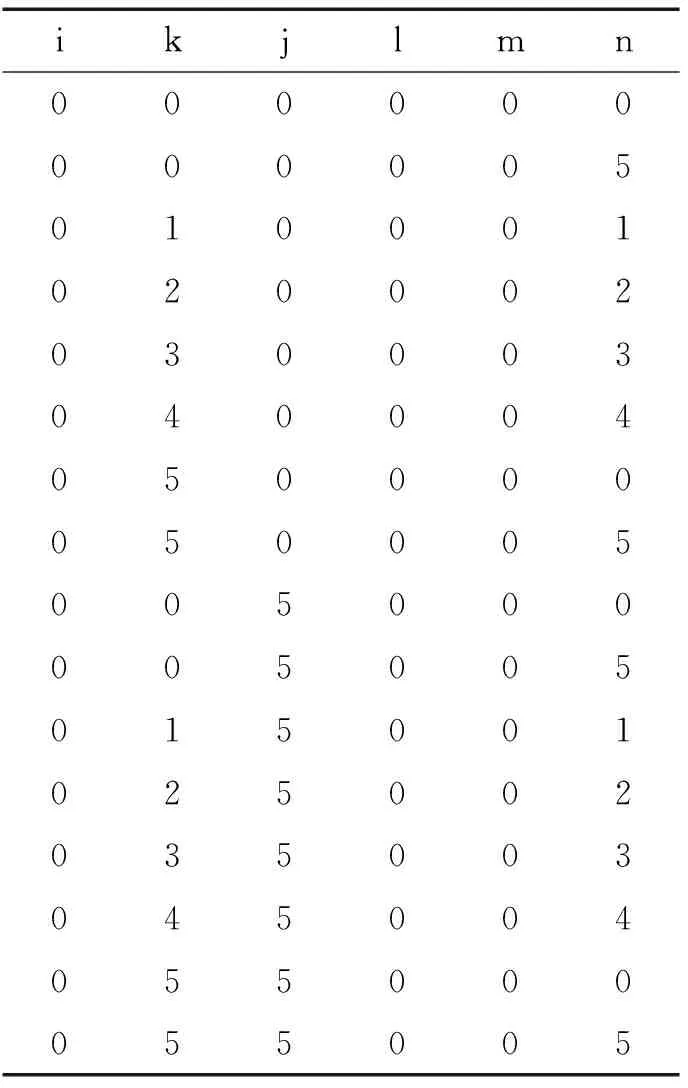
表3　式(10)检验结果

的全部非负整数解(a，b，c，d，e，f)由引理中的表1(a)给出。

证明设(x，y，z，u，v，w)是方程(1)式的任一组解时，由引理1，可设

(x，y，z，u，v，w)=(a+60i，b+120j，c+60k，d+120n，e+60l，f+60m)，

其中(a，b，c，d，e，f)是表1中的任一组数。当(a，b，c，d，e，f)由引理表1(a)或表1(b)给出时，注意到表1(a)和表1(b)的任一组数是方程(1)的解，我们有

2a11b(260i11120j-1)+5c11d(560k11120n-1)

=2e5f(260l560m-1)。

(5)

(ⅰ)当(a，b，c，d，e，f)=(3，0，0，1，2，1)时，有

23(260i11120j-1)+11(560k11120n-1)

=22·5(260l560m-1)。

(6)

依次对(6)取模11，5，8，得j=k=l=0，再取模25，得m=0，从而i=n=0。故有(x，y，z，u，v，w)=(3，0，0，1，2，1)，它是方程(1)的满足题设条件的一组解。

同理，当(a，b，c，d，e，f)=(3，0，0，0，1，1)和(a，b，c，d，e，f)=(2，0，1，0，1，1)时，必能推出(x，y，z，u，v，w)=(3，0，0，0，1，1)和(2，0，1，0，1，1)，因为它们不满足方程(1)的限制条件，所以不是方程(1)的解。

(ⅱ)当(a，b，c，d，e，f)=(2，1，1，1，2，2)时，有

22·11(260i11120j-1)+5·11(560k11120n-1)

=22·52(260l560m-1)。

(7)

对(7)取模25，得k=0。若i≠0，模8，得l≠0，再取模16，有-8≡0(mod16)的矛盾，故i=l=0。由于δ151(560)=δ151(11120)=5，在0≤j，m，n≤5范围内，在计算机上对同余式

22·11(260i11120j-1)+5·11(560k11120n-1)

≡22·52(260l560m-1)(mod101·151)。

(8)

进行检验，可得j≡n≡0(mod5)，如表2所示。对(7)取模53，可得m=0，从而j=n=0。故有(x，y，z，u，v，w)=(2，1，1，1，2，2)，它是方程(1)的满足题设条件的一组解。

同理，当(a，b，c，d，e，f)=(2，1，1，0，1，2)和(a，b，c，d，e，f)=(3，1，0，1，2，2)时，必能推出(x，y，z，u，v，m)=(2，1，1，0，1，2)和(3，1，0，1，2，2)，它们都是方程(1)的满足题设条件的一组解。

(ⅲ)当(a，b，c，d，e，f)=(2，1，2，1，6，1)时，有

22·11(260i11120j-1)+52·11(560k11120n-1)=26·5(260l560m-1)。

(9)

依次对(9)取模23，25，得i=m=0。由于δ151(260)=1，δ151(560)=δ151(11120)=5，在0≤j，k，n≤5，0≤l≤1范围内，在计算机上对同余式

22·11(260i11120j-1)+52·11(560k11120n-1)≡26·5(260l560m-1)(mod101·151)

(10)

进行检验，可得j≡0(mod5)，如表3所示，对(9)取模53，可得k=0。由于δ193(260)=δ193(11120)=8，在0≤j，n，l≤8范围内，对同余式

22·11(260i11120j-1)+5·11(560k11120n-1)≡22·52(260l560m-1)(mod97·193)

(11)

进行检验，可得j≡n≡0(mod8)，如表4所示，对(9)取模27，可得l=0，从而j=n=0。故有(x，y，z，u，v，w)=(2，1，2，1，6，1)，它是方程(1)的满足题设条件的一组解。

表4　式(11)检验结果

表5　式(13)的检验结果

表6　式(14) 的检验结果

(ⅳ)当(a，b，c，d，e，f)=(7，0，0，2，1，3)时，有

27(260i11120j-1)+112(560k11120n-1)

=2·53(260l560m-1)。

(12)

依次对(12)取模11，5，4，得j=k=l=0。由于δ193(260)=δ193(11120)=8，δ193(560)=16，在0≤i，n≤8，0≤m≤6范围内，在计算机上对同余式

27(260i11120j-1)+112(560k11120n-1)

=2·53(260l560m-1)(mod97·193)。

(13)

进行检验，得n≡0(mod8)，m≡0(mod16)，如表5所示，对(12)取模28，可得i=0。由于δ2251(11120)=25，δ2251(560)=25×27，在0≤m≤25×27，0≤n≤25范围内对同余式

27(260i11120j-1)+112(560k11120n-1)

≡2·53(260l560m-1)(mod101·151·2251)。

(14)

进行检验，得n≡0(mod25)，如表6所示。对(12)取模54，可得m=0，从而n=0。故有(x，y，z，u，v，w)=(7，0，0，2，1，3)，它是方程(1)的满足题设条件的一组解。

(ⅴ)最后证明(a，b，c，d，e，f)=(14，61，29，19，58，38)和(54，31，13，19，38，18)时，方程(1)没有满足题设条件的解。

假设上述2组数都是方程(1)的解，则它们满足方程(5)，且必有k>0，使

2a11b(260i11120j-1)+5c11d(560k11120n-1)

≡2e·5f(260l560m-1)(mod101·151·401)。

(15)

由于δ401(260)=10，δ401(560)=δ401(11120)=5，所以只需对(a，b，c，d，e，f)的上述2组取值的每一组在0≤i，l≤10， 0≤m，k，n，j≤5范围内检验(15)式是否成立。用UBASIC编写了检验程序，经计算机检验得知，无0≤i，l≤10， 0≤m，k，n，j≤5使(15)式成立，故方程(1)没有解。

参考文献：

[1]曹珍富.丢番图方程引论[M].哈尔滨:哈尔滨工业大学出版社,2012.

[2]曹珍富.关于阶为2α13α25α37α4pα5的单群[J].数学年刊,1995,16A(2):244-250.

[3]BRENERJL,FOSTERLL.ExponentialDiophantineequations[J].Pacific.Math, 1982, 101:263-301.

[4]ALEXLJ,FOSTERLL.OntheDiophantineEquation1+x+y=z，withxyz=2r3s7t[J].ForumMath, 1995, 7(6):645-663.

[5]邓谋杰,李春燕.关于丢番图方程1+2x7y+2z5u7v=5w[J].吉首大学学报(自然科学版),2009,30(04): 1-3.

[6]邓谋杰.关于丢番图方程1+5x=2y7z+2u5v7w[J].黑龙江大学自然科学学报,2010, 27(01):16-18+33.

[7]李春燕,邓谋杰.关于丢番图方程1+X+Y=Z [J]. 海南大学学报(自然科学版),2010,28(02):102-104.

[8]宋容炎,邓谋杰.关于丢番图方程1+7x=2y5z+2u5v7w[J].吉首大学学报(自然科学版),2011,32(01):4-6.

[9]刘静,邓谋杰.关于丢番图方程2x+2y=3z11u=3v11w[J].黑龙江大学自然科学学报,2012,29(06):723-726.

[10]周小娥 ,邓谋杰.关于丢番图方程px-qy=2 [J]. 海南大学学报(自然科学版),2013,31(02): 100-102+105.

OntheDiophantineEquation1+2x11y+5z11u=2v5w，xvw>0，y+u>0

CHENXiaoyan

(DepartmentofmathematicsandPhysics,QiongtaiTeachersCollege,HaikouHainan571100,China)

Abstract:This paper discusses a special case of the Diophantine equation 1+X+Y=Z.With computer assistance,all the nonnegative integer solutions to the exponential Diophantine equation 1+2x11y+5z11u=2v5w，xvw>0，y+u>0 are determined by elementary method.

Keywords：exponential diophantine equation;congruence solution;solutions in non-negative integers;computer-aided solution

文章编号：1673-5072(2016)02-0200-03

收稿日期：2015-06-26

作者简介：陈小燕(1982—)，女，海南临高人，讲师，主要从事数论研究。 通讯作者：陈小燕，E-mail:837448518@qq.com

中图分类号：O156.7

文献标识码：A

DOI：10.16246/j.issn.1673-5072.2016.02.014