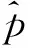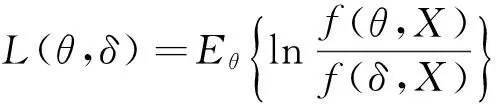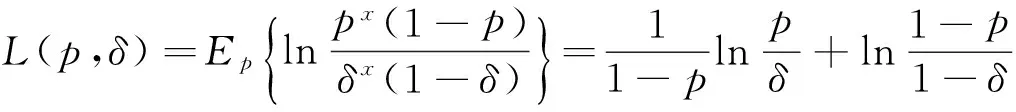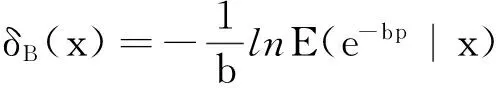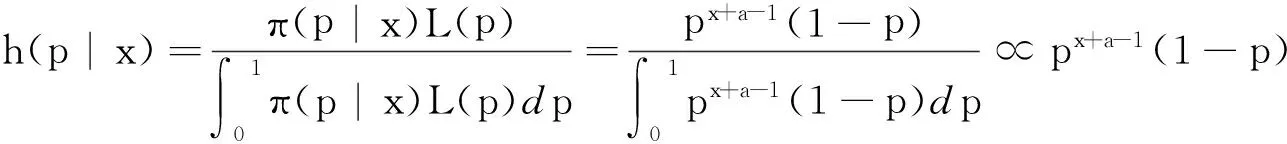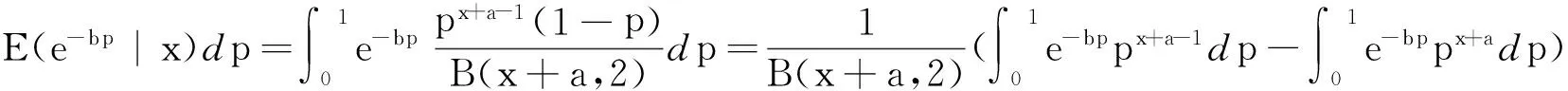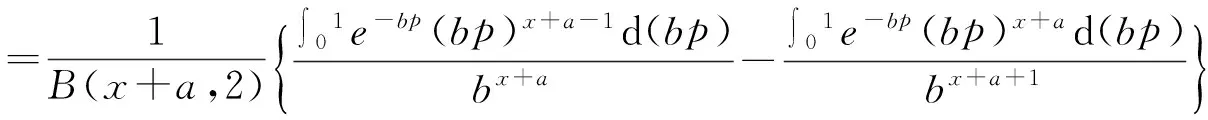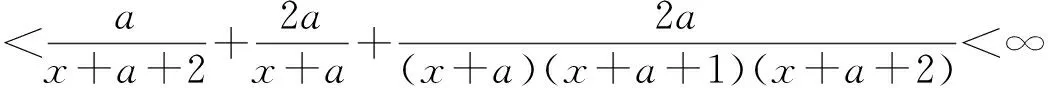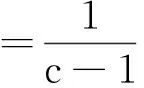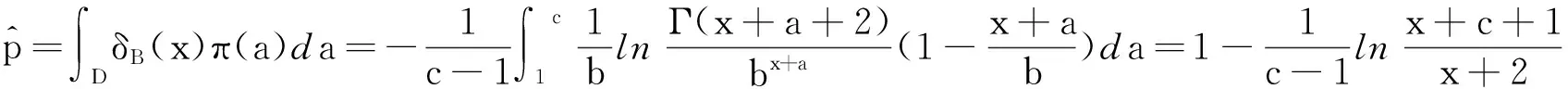不同损失函数下几何分布参数的EB估计
熊常伟,张 怡
(1.南充市统计局,四川 南充 637000;2.西华师范大学 数学与信息学院,四川 南充 637009)
不同损失函数下几何分布参数的EB估计
熊常伟1,张怡2
(1.南充市统计局,四川 南充637000;2.西华师范大学 数学与信息学院,四川 南充637009)
摘要:当几何分布可靠度的先验分布为幂分布时,推算出了Linex损失函数下其可靠度的Bayes估计,用反证法证明了该估计的唯一性,推算论证了该估计风险有限和可容许性。根据E-Bayes估计的定义推算出了Linex损失函数下几何分布可靠度的EB估计。结合实际数据比较了熵损失函数和Linex损失函数下几何分布可靠度E-Bayes估计值的稳健性和精度并得出有效结论。
关键词:几何分布;幂分布;熵损失函数;Linex损失函数;EB估计
在测试产品寿命的研究中常运用几何分布的可靠性分析。文献[1]验证了几何分布E-Bayes估计比多层Bayes估计精度高。文献[2]验证了其在熵损失函数下的Bayes估计,文献[3]推广到Q对称熵损失函数下,其估计精度均较高。文献[4]验证了几何分布可靠度的先验分布为幂分布时其Bayes估计精度高。结合前面的研究成果,本文将在Linex函数下验证其可靠度的Bayes估计,在证明了该估计的唯一性和可容许性后,推算出了其E-Bayes估计,并与其在熵损失函数下的E-Bayes估计进行比较。
1四个定义[5-8]
定义1[5]在贝努利实验中,若P为系统实验成功的概率(可靠度),如果进行了x+1次实验,前x次试验成功而第x+1次不成功(失败)的概率为:
P(X=x)=px(1-p),k=0,1,2...,0 (1) 称随机变量X服从几何分布,其中参数P为几何分布的可靠度(或成功概率)。 定义3[6]随机变量X的密度函数为f(θ,δ),其中θ为参数,δ是θ的估计,其熵损失函数表达式为: 则几何分布的熵损失函数为: 此损失函数关于δ是严格凸的。 定义4[7,8]Linex损失函数定义:在Linex非对称损失函数即 L(p,δ)=eb(δ-p)-b(δ-p)-1 (2) 意义下考虑参数P的估计,其中δ为P的估计值,b为该损失函数的尺度参数,b∈R且b≠0,本文仅考虑b>0的情形。 2Linex损失函数下可靠度p的E-Bayse估计 2.1Linex损失函数下可靠度p的Bayse估计验证 定理1在先验分布和Linex损失函数(2)式下,几何分布可靠度p的Bayes估计为: 该估计是唯一的,其风险r(δ)<∞。 证明在表达式(2)下,估计值的Bayes风险为: r(δ)=E[L(p,δ)]=E(E[L(p,δ)]|X)=E(E[eb(δ-p)-b(δ-p)-1]|X)。 等式左端是关于p和x的联合分布期望,极小化E[eb(δ-p)-b(δ-p)-1]|X]可以使上式达到最小,即使ebδE(e-bp|X)-bδ+bE(p|X)-1达到最小。对上式关于δ求导并令其为0,即 : ebδbE(e-bp|x)-b=0, ebδbE(e-bp|x)=1, ebδ=E(e-bp|x)-1。 如r(δB)(x)<∞,可以证明该解的唯一性。由题设可知r(δ)<∞,而r<(δB) 根据文献[4]当p的先验分布为幂分布时精度较高,即: π(p|a)=apa-1, (3) 其中0 则: 此式中构造伽玛函数[7]Γ(s,t)=∫01xt-1e-xdx, 即: 伽玛函数间的性质[6]:Γ(1)=1,Γ(a+1)=aΓ(a),Γ(n+1)=nΓ(n)=n!, (4) 下面证明δB(x)对应的Bayes风险有限: 比较Bayes风险等同于比较∫ΘL(p,δ(x))P(x|θ)π(θ)dθ的大小(其中:Θ为参数空间)[9,10],则: r(δB(x))=∫pL(p,δB(x))P(x|p)π(p|a)dp =a∫01px+a(lnp-lnδB)dp+a∫01px+a-1(1-p)[ln(1-p)-ln(1-δB)]dp 根据Bayes决策可容许估计的定理,P的Bayes解是可容许估计。 2.2可靠度p的E-Bayes估计 证明对几何分布(1),若p的先验分布π(p)为幂分布(3),p的Bayes估计由(4)给出,根据定义2p的E-Bayes估计为: 3熵损失函数下可靠度的E-Bayse估计 4结果检验 在寿命检测的连续试验中,第25次首次出现失败[1],根据文中的推导结论,可以得出可靠度EB估计值。见表1(2≤c≤6)。从表1可以看出,当2≤c≤6时,极差很小,可靠度的计算结果是稳健的。 表 1 可靠度的估计结果 5结束语 本文在Linex损失函数下推算出了几何分布可靠度的Bayes估计,验证了其容许性和唯一性,根据定义推算出其EB估计。比较两种损失函数下的EB估计,从具体数值演算结果可看出这两种函数下的EB估计公式都与实验值接近,相比之下熵损失函数下的EB估计更稳健。 参考文献: [1]熊常伟,张德然,张怡,等.几何分布可靠度的Bayes估计[J].统计与决策,2007,23(20):21-22. [2]熊常伟,张德然,张怡.熵损失函数下几何分布可靠度的Bayes估计[J].数理统计与管理,2008,27(1):82-86. [3]熊常伟,张德然,张怡.Q对称熵损失下几何分布的参数估计[J].贵州师范大学学报(自然科学版),2007,25(3):36-39. [4]熊常伟,张德然,张怡.不同先验分布下几何分布参数的E-Bayes估计[J].阜阳师范学院学报(自然科学版),2007,24(3):42-46. [5]茆诗松.概率论与数理统计教程[M].北京:高等教育出版社,2003. [6]茆诗松.贝叶斯统计[M].北京:中国统计出版社,1999. [7]张丽.Linex损失下几种分布参数的Bayes估计及性质[D].兰州:兰州交通大学,2011. [8]李俊华.复合Linex对称损失函数下几何分布参数估计[J].长江大学学报(自然科学版),2011,8(4):32-35. [9]韩明,催玉萍.几何分布可靠度估计[J].运筹与管理,2001,10(4):35-38. [10]赵喜林.几何分布可靠度的截尾Bayes估计[J].武汉科技大学学报(自然科学版),2004,3(1):93-95. ExpectBayesEstimationOfGeometricDistributionParameterUnderDifferentLossFunction XIONGChangwei1,ZHANGYi2 (1.StatisticalBureauofNanchong,NanchongSichuan637000,China;2.CollegeofMathematicsandinformationinstitute,ChinaWestNormalUniversity,NanchongSichuan637009,China) Abstract:This paper finds when the prior distribution of the geometric distribution reliability is the power distribution,the estimation of the reliability of Bayes is reckoned under the Linex loss function.The uniqueness of the estimation is proved by the method of reduction to absurdity,which demonstrates the limitation and the admissibility of the risk.According to the definition of the E-Bayes estimation,the EB estimation of the geometric distribution reliability is reckoned under the Linex loss function.Combined with the actual data,the paper compares the precision of the EB estimation of the geometric distribution reliability under entropy loss function and Linex loss function,and the effective conclusions are made. Keywords:geometric distribution;power distribution;entropy loss function;Linex loss function;Expect Bayes estimation 文章编号:1673-5072(2016)02-0206-04 收稿日期:2015-07-09 基金项目:西华师范大学校基金项目(14D015) 作者简介:熊常伟(1981—),男,四川大竹人,硕士,主要从事概率论与数理统计。 E-mail:zhangyi318lw@163.com 通讯作者:张怡(1982—),女,四川南充人,副教授,主要从事灰色系统理论、不确定信息系统、概率论与数理统计研究。 中图分类号:O211.3 文献标识码:A DOI:10.16246/j.issn.1673-5072.2016.02.016