数学考试成绩与主要知识模块的灰色关联度分析及教学策略
余远泽


【摘要】本文以一次全柳州市文科数学考试成绩为例,利用统计学的灰色关联度分析法定量分析了文科数学科不同模块对数学考试成绩的贡献度,结果表明集合、向量、不等式、二项式定理等对单科成绩的贡献度最大,排第2位的是函数及导数,数列贡献第3,立体几何的贡献度最小.对研究结果进行了分析,并制定了下一阶段文科数学教学的基本策略.
【关键词】数学考试;灰色关联度分析;立体几何;策略
本文以高三文科数学三模考试成绩为例,利用统计学的灰色关联度分析法定量分析数学科不同知识模块对数学考试成绩的贡献度.考察不同板块对于数学科考试成绩的关联性、贡献度,找出薄弱板块,对研究结果进行分析,并制定了下一阶段数学教学的基本策略.
一、方法和分析
灰色系统中关联度分析是对于一个发展变化系统进行发展态势的量化比较.其基本思想是根据曲线的几何形状的相似程度来判断关联程度.
本次考试我校2014届高三全市三模数学文科考试成绩,有效试卷248份,采用全市集中、统一电脑阅卷.本次考试单科成绩可以看作一个灰色系统,各知识板块即该灰色系统中的子系统.如下表:
按关联分析原则,各板块的关联度即其贡献度,在本例中,本次高三三模数学(文科)考试,从全年级来看,对于单科总分贡献最大的是其他(集合、向量、不等式、二项式定理),其次是函数及导数,再次是数列,第四位的是概率及排列、组合,第五位的是三角函数,第六位的是解析几何,贡献度最小的是立体几何.
二、结果分析及基本策略
1.试题的分析
试题各知识板块的分值与历届高考试题基本相似,只是三角函数和函数及导数的分值有些变化,加重了函数及导数考察、减少了三角函数的分值,只是更注重知识的综合应用和能力的体现,是一份能体现现价段要求的试题.
2.结果分析
对本次考试的数据进行定量分析之后,笔者和数学备课组的老师进行了研究、讨论,并部分学生进行了访问.数据的定量分析与数学备课组的定性分析结果相符.主要表现在:
(1)其他(集合、向量、不等式、二项式定理)这个板块,一般情况下考察的难度不大,注重于考察基本的知识和基本能力,关联度排序排第一位,说明上学期一轮复习比较有成效,为高考数学奠定了扎实的基础.
(2)数列和概率及排列、组合这两个板块,分值、难度都比较稳定,关联度排序排应靠前列,这和分析的结果相符合,说明这两块的复习比较正常.
(3)由于函数和导数这个板块的概念比较抽象,涉及的数学思想和方法比较多,要求又比较高,对文科学生来说是个难点,但关联度排序排第二,是本次考试的一个亮点,原因是刚结束函数和导数这个板块的专题复习.从中得出结论,后面的专题复习要科学地设计好,它是提高学生能力和进行程序化解题的关键.
(4)存在的问题:三角函数这个板块,是文科数学难度最低,必须拿分的板块之一,但这个板块关联度排序排相对靠后,该模块对于数学科成绩的贡献度上升的空间还很大,是重点要加强和突破的板块.立体几何重点考察学生的空间想象力和空间思维能力的板块,对文科生,特别文科女生是特别困难的事,但高考数学要上一本线,这个板块必须基本拿下,引入了空间向量法以后,为立体几何的突破提供了可能和方法,立体几何是本次考试中对单科成绩中贡献度最小的,是今后复习一定要突破的.
3.基本策略(以立体几何为例)
(1)专题复习是提高学生各个板块能力的有效途径,要注重学科知识体系,基本能力,基本方法的梳理,从而形成知识网络.因此,要借助思维导图进行专题复习,如立体几何可用如下思维导图进行归纳、整理;还必须要求学生自己绘制不同的思维导图对知识、方法、类型进行梳理,进一步形成能力.
(2)要深入研究历届高考题,对各版块的类型、方法、数学思想进行归纳、对比、提升,从而形成程序性知识,进一步通过适当的练习,形成策略性的知识和方法.例如,立体几何在高考文科数学(大纲卷)中重点考察空间的夹角和距离,传统的方法是找(作)、证、求,要求学生有较强的空间思维能力,这对文科学生来说,相当困难,空间向量法是文科生突破这个板块难点的非常有效的方法,只需解决以下两个难点:
1.突破建系
(1)空间的垂直关系是建系的基础,要重点加强空间垂直的复习,要注重空间线线垂直、线面垂直、面面垂直的判定和性质的应用,以及它们之间的相互转换.线线垂直是基础,线面垂直是核心,面面垂直是关键,利用线面垂直找出Z轴(或Z轴的平行线),利用面面垂直的性质定理(在一個平面作垂直于交线的直线垂直于另一个平面),转化为线面垂直,从而找出Z轴.
(2)底面平面化的方法,研究底面线线垂直关系,找出X轴、Y轴.
(3)要有效地结合数学思想,如分割法、补形法.
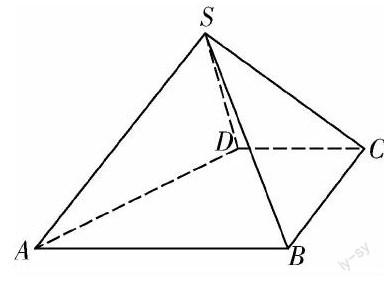
例1 (2011年大纲版高考题20)如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=SD=1.
(1)证明:SD⊥平面SAB,
(2)求AB与平面SBC所成角的大小.
思路分析
难点:如何建系.
突破点:分割,面面垂直性质定理,底面平面化.
因为底面直角梯形ABCD分割成矩形BCDE和直角三角形DEA,四棱锥S-ABCD分割成一个底面是直角的三棱锥S-DEA和一个底面是矩形的四棱锥S-BCDE,证出平面SDE⊥底面ABCD,利用面面垂直的性质定理,过S作SF⊥DE于F点,从而SF⊥底面ABCD,得出Z轴,如图1,把底面平面化,如图2,找出X轴、Y轴,最后,如图3建立空间直角坐标系,剩下的问题易解决.
思路分析
难点:如何建系.
突破点:补形,面面垂直性质定理,底面平面化.
把底面四边形ABC0D补成正方形ABDE和直角三角形BC0D,由第一问易证平面COC0⊥底面ABC0D,如图(4).利用面面垂直的性质定理,过C作CO⊥C0D的延长线于O点,从而CO⊥底面ABC0D,得出Z轴,易证三角形CED为等边三角形,把底面平面化,如图(5),找出X轴、Y轴,最后,如图(6)建立空间直角坐标系,剩下的问题易解决.
2.突破设参、求点坐标
(1)底面上的点,底面平面化后,画出底面平面图形,由平面几何的知识及图形的性质,求出个点的坐标.
(2)空间的点,找(作)出底面的垂线,能判断垂足在底面的位置的,问题就解决了,有些斜棱柱上的点,很难判断垂足在底面的位置,可以采用平行向量,坐标相等的方法,或用向量加法的三角形法则,求点的坐标.
(3)对于一些存在性问题、共线问题,采用设参、求参的方法(根据题目给出的条件,如空间线线垂直、平行,空间线线角、线面角、面面角,空间点面距离列关于参数的方程,解方程求出参数).
总之,教学、备考是一项系统工程,有其内在的规律和特点,深入研究并掌握相应的方法,将取得事倍功半的效果.运用统计学方法如灰色关联度分析,发现教学过程中的问题,从而针对问题制定改进策略,尤其是针对高中文科数学不同知识内容采取具体、有效且独到的教学方法来突破难点、瓶颈,是一个教育工作者应尽的责任,是“在教学中科学研究,从科学研究中启发教学”真正体现.
【参考文献】
[1]袁嘉祖.灰色系统理论及其应用[M].北京:科学出版社,1991.
[2]东尼·博赞.思维导图——大脑使用说明书[M].北京:外语教学与研究出版社 2005.4.
[3]张德峰.高中数学解题教学研究[J].数学学习与研究,2010(09).
[4]徐斯亮.高中数学解题常用的几种策略[J].数理化解题研究(高中版)2009(07).

