立体几何中策略创造的培养
罗莎


【摘要】数学的学习是一个再创造的过程,教师提供学生数学学习中再创造的平台.学生的策略创造培养,是一个长期的过程,对于策略创造的培养,可能是一种思想方法的迁移应用,也可能是一个基本知识点的发散训练.本文就立体几何中空间直角坐标系的方法的应用,可将学生无法入手的问题,变成有法可解,有规律可循;
【关键词】策略创造;空间直角坐标系
数学的学习是一个再创造的过程,教师提供学生数学学习中再创造的平台.张奠宙教授认为:“数学教学的任务之一,是将逻辑演绎编写的教材还原成生动活泼的思维创造活动”[1].同时张奠宙教授认为:“数学思维是策略创造和逻辑演绎的结合,而且策略创造处于主导方面,逻辑演绎是基础方面”[1].对于学生创新思维的培养,离不开学生的策略创造.学生的策略创造培养,是一个长期的过程,逐步生成,它有可能是“观察实验,引发猜想;数形结合,萌生构想;类比模拟,积极联想;发散求异,多方设想;思维设计,允许幻想;直觉顿悟,突发奇想;群体智力,民主畅想”[2].在教学过程中,实现培养学生的策略创造,教师就要提供再创造的阶梯,以一步一步的培养和激励学生策略创造的活动.
教师提供再创造的一个环节,可以是一种思想方法的针对性渗透.比如,立体几何中的传统法需要很强的空间感,解决有的问题时学生感到吃力.向量方法或空间坐标系法在课本中,主要解决线线,线面,面面的夹角问题,但教师可以将该方法进行渗透,让学生思维得到发散,让学生体会到从“形”到“数”的过程的乐趣.在此,区别于综合证明的向量法或空系法就为数学学习提供了一个再创造的平台,利用空间坐标系这个基本工具,将难以构造的空间图形问题数值化,实现从“无”到“有”,使得许多问题迎刃而解.
一、发散求异,多方设想
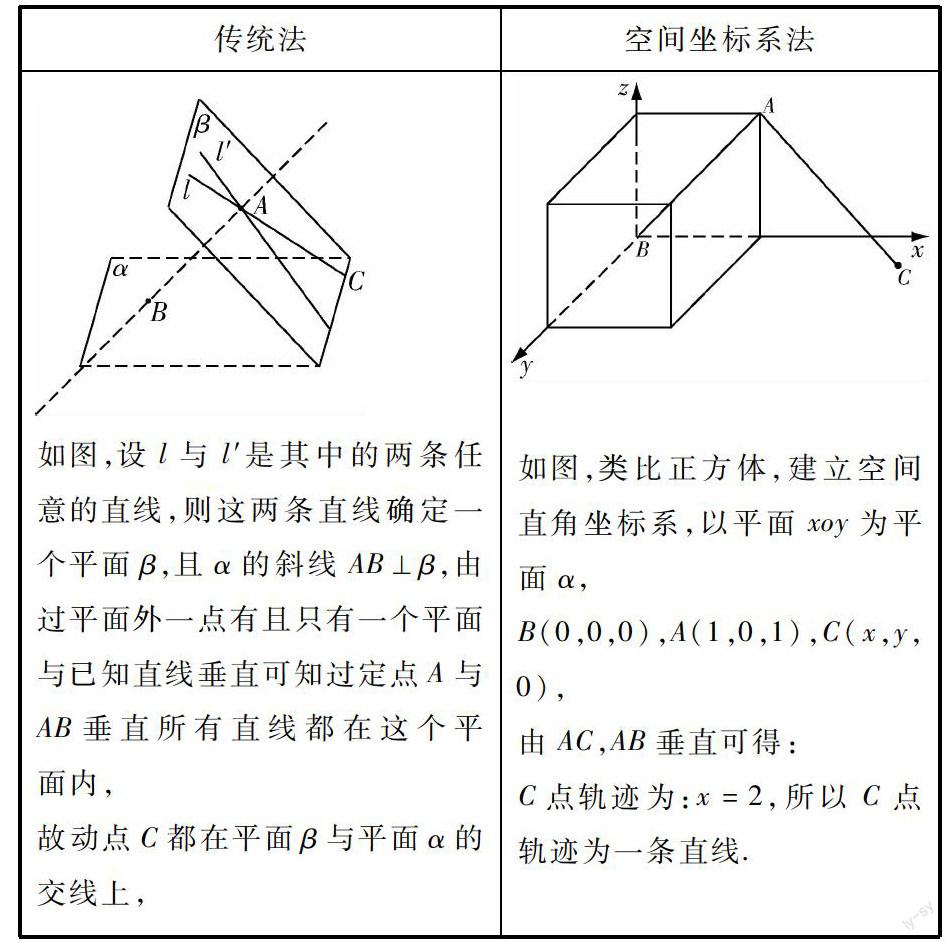
例1 一只小球放入一长方体容器内,且与共点的三个面相接触,若小球上一点M到这三个面的距离为4,5,5,求这只小球的半径?
在传统法中,学生难以想象O,M,N,的结构关系,难以通过直角三角形确定|MN|的值,因此增加了思维难度;但是通过空间直角坐标系的建立,不需要寻找|MN|有关直角三角形的转化,直接利用两点间距离公式,寥寥数语就可表达清楚.可谓是柳暗花明又一村,让学生充分体验到“数”能定“形”.
二、类比模拟,积极联想
例2 平面α的斜线AB交α于点B,过定点A的动直线l与AB垂直,且交α于点C,则动点C的轨迹是什么?
通过类比联想,以正方体为载体,将一般问题特殊法.同时,传统法中学生难以想到构造平面β,空系法不需要平面β的构造,直接转化到线线垂直,一个垂直公式便将问题迎刃而解.
三、思维设计,允许幻想
例3 已知正方体ABCD-A1B1C1D1的棱长为1,动点P在正方体ABCD-A1B1C1D1表面上运动,且PA=r(0本题难度较高,主要考察的是对新定义的快速理解应用.题目中的函数f表示的是满足到正方体一点为定长的正方体表面的点的轨迹长度.
第一空f1[]2表示到点A距离为0.5的点构成的曲线长.即三个面的半径为0.5的四分之一圆弧长度之和,即f1[]2=3[]4π.
第二问在第一问基础上,但较难,f(2)即表示到点A距离为2的点构成的曲线长,由分析可知,f(2)为三面相同的曲线之和,由于2>1,如何在正方体表面上表达点A距离为2的点构成的曲线长,有学生可能猜到为圆弧,但圆弧对应的半径又是多少呢?如何解决这个问题,前面两道例题已经提供了思路,建立空間直角坐标系可以找到轨迹问题.如右图,设P点在上顶面,则P(x,y,1)PA=2,则P点轨迹为半径为1的四分之一圆弧.所以f(2)=3[]2π.
向量的思想和空间直角坐标系的建立将立体几何进行了三维代数化,教师提供有效的通道让学生体会到从“形”到“数”的过程.对于策略创造的培养,可能是一种思想方法的迁移应用,也可能是一个基本知识点的发散训练.本文就立体几何中空间直角坐标系的方法的应用,可将学生无法入手的问题,变成有法可解,有规律可循;学生要能够实现策略创造,并不是天马星空的乱象,而是在自身数学活动的经验中提取出来的,而教师正式这些活动的提供者之一.
【参考文献】
[1]张奠宙等编著,现代数学家传略辞典,南京:江苏教育出版社,2001.
[2]张大国,孙素慧,数学学习中创造性思维的培养,教学与管理,2008,18,84-85.

