面向场地鉴定的MLS脉冲定时点测量误差量化分析方法

唐　茂，李晓明，李承奉，邓历翔

(1. 中国人民解放军94683部队，福建 晋江 362200; 2. 空军工程大学 信息与导航学院，西安 710077；



面向场地鉴定的MLS脉冲定时点测量误差量化分析方法

唐茂1，李晓明2，李承奉3，邓历翔1

(1. 中国人民解放军94683部队，福建 晋江 362200; 2. 空军工程大学 信息与导航学院，西安 710077；

3. 中国人民解放军94857部队，安徽 芜湖 241000)

摘要：针对多径效应引起MLS(microwave landing system)信号包络畸变造成脉冲定时点测量误差问题，提出了一种改进的误差量化分析方法。通过对误差量化分析流程的分析，指出造成误差的关键因素，并根据包络信号的形式，提出假设条件，简化模型，导出修正后的误差量化分析公式，同时对量化分析公式精度进行分析。仿真结果表明，该方法能定量分析多径效应引起的脉冲定时点测量误差。

关键词：微波着陆系统；多径效应；定时点误差；量化分析

0引言

随着微波着陆系统(microwave landing system，MLS)大力推广和广泛使用，其在工作过程中遇到了各种各样的问题，比较突出且常见的就是场地环境效应问题。场地环境效应问题是指由停靠飞机、建筑物、起伏地形等各类障碍物构成的场地环境不规范引起的MLS引导能力下降问题。量化该问题首先需要对MLS台站进行场地鉴定。场地鉴定是指鉴定导航台站场地对导航设备的适应性。具体内容是对由场地环境效应问题对MLS引导能力影响程度的评估。传统场地鉴定主要是依据国际民航组织(international civil aviation organization ,ICAO)相关规范和操作人员的经验施行的，是一种粗略的、定性的评估，缺少对场地效应的量化分析[1]，而场地环境效应的主要因素是多径干扰[2]。多径干扰导致MLS接收到的“往”“返”脉冲包络形状畸变，引起定时点测量误差造成MLS定位精度降低。因此，可以通过量化多径效应引起的脉冲定时误差来定量评估场地效应，从而实现场地鉴定的量化评估。

目前，ICAO采用的MLS场地效应测角误差分析的方法是由美国俄亥俄大学的Mathias等人在20世纪90年代提出的Mathias误差分析法[3-5]。该方法可以快速分析和计算场地环境效应引起的测角误差，但是，该方法仅考虑了分离角约为半主瓣宽度情况以及只计算了脉冲波束后沿的定时点误差，存在局限性。戴传金等人利用波束替代法[6-8]，简化脉冲模型后利用函数误差理论，经过一系列的近似后得到一个误差的量化公式，该公式考虑到多径信号相对于直达信号的幅度比和相位差等因素，并包含了脉冲前、后沿2个误差因素，改进了Mathias误差分析法，弥补其局限性。但是该方法在化简求解中忽略了一些重要量，造成一定的误差。由于MLS测角精度很高，因此要求一个精度较高的量化误差分析方法。

针对现有的MLS多径测角误差量化方法的不足，本文在戴传金等人的研究基础上，提出了一种改进的误差量化方法。通过对误差量化分析流程的分析，引起脉冲定时点测量误差的主要因素，并根据包络信号形式上的特点，提出假设条件，合理简化模型，得到改进的误差量化分析公式。此方法根据信号参数定量分析测角误差，可以实现对场地效应的量化评估。

1MLS测角原理及扫描波束包络误差

MLS系统,是在方位角和仰角扇区以内,用2个窄波束以均匀速度v,分别进行左右和上下扫描，当处于某个角位置θ的飞机收到该扫描信号时，就在与θ对应的时间上产生相应的“往”“返”脉冲 。机载接收机将在视频信号中捕获这一对扫描脉冲，首先找到峰值电平信号(“往”“返”扫描直达脉冲的主波瓣),其次验证它们相对于扫描中心的对称性。如果不符合对称性,那么必然有1个假信号，只有符合对称性才说明它们是真实的“往”“返”脉冲。经证实是直达信号后,测定其振幅并进行包络处理[5]。

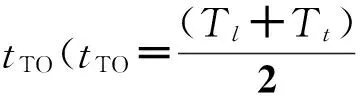
(1)

(1)式中:θ(rad)为待测方位角；T0(ms)为往返扫描经过跑道中心0°角位置的时间间隔，为设计常数；t0(ms)为扫描脉冲中心点从“往”到“返”的时间间隔；v(rad/ms)为扫描速度，一般取v=20 rad/ms。

图1　接收机锁住闸门脉冲时间间隔测量Fig.1　Time alternation measurement process ofreceiver dwell gate pulses

当接收信号中混叠了多径信号之后，接收到的“往”“返”信号包络发生畸变，将影响脉冲定时点的测量，如图2所示。

图2　脉冲包络中心偏移示意图Fig.2　Pulse envelope center offset diagram

直达信号与非直达信号叠加，使得原来的脉冲包络发生畸变，从图2可以看出“往”(“返”)脉冲的后沿向后(前)拓展了，使得“往”(“返”)脉冲的定时中心向后(前)偏移，最终影响了脉冲定时点的选取，造成测角误差。

多径效应使得脉冲包络发生畸变，采用传统方法测角将引起较大误差，该误差表征了场地环境对MLS制导精度的影响。

2包络误差量化分析方法

信号包络e(θ)定义为直达信号和非直达信号叠加而成的混叠信号包络[6]

(2)

(2)式中：A(θ)为直达信号包络;ρi，θi，δi分别为非直达信号相对直达信号幅度比，角度差和载波相位差。

从MLS测角原理出发，欲求混叠信号包络定时点，需要求得信号包络的幅度峰值以及其半值门限与脉冲前后沿交点对应的时刻[9]。可分为如下步骤：

Step 1利用(2)式求得包络幅度峰值;

Step 2取峰值半幅作为门限电平，利用门限电平对脉冲包络进行限幅得到一个矩形脉冲，再求得矩形脉冲前后沿时刻;

Step 3将前后沿时刻的中间时刻作为脉冲定时点。

多径效应影响的是Step 1幅度峰值和Step 2脉冲前后沿时刻，现对多径情况下的Step 1和Step 2进行分析。其中峰值位置的变化和脉冲前后沿的变化时决定脉冲定时点的关键因素，故作为重点介绍。

2.1峰值位置变化

从MLS测角原理的步骤Step1知，要求包络幅度峰值需先求得(2)式包络

(3)

(3)式可以继续化简，其化简条件将在仿真分析中具体给出。(3)式化简可得

(4)

对(4)式左右两边求对数，可得

2ln|e(θ)|=2lnA(θ)+

(5)

令

f(θ)=2lnA(θ)+

(6)

由函数性质知(6)式与(5)式有相同的单调性。(6)式中的极值与(5)式中极值相对应。故可以通过求(6)式的极值来确定(5)式的极值。

若x∈U(0,ξ)，则ln(1+x)～x，故可将(6)式近似为

(7)

(7)式求导得

(8)

此时引入一个假设

(9)

(10)

结合(9)式，(10)式可以继续化简

(11)

由x∈U(0,ξ),ex～1+x可将(11)式简化为

(12)

2.2脉冲前后沿时刻变化

由测角原理知从脉冲信号包络峰值衰减到其-3dB处，脉冲前后沿各有一个时刻点与之对应，这两个时刻点就是脉冲前后沿的定时点。现在设定-3dB门限法确定脉冲前后沿的数学模型为

(13)

(14)

对(13)式左右两边取对数得

(15)

令

(16)

(16)式中，ε+，ε-分别为脉冲前后沿误差。将(14)式及(16)式代入(15)式中可化简解得

(17)

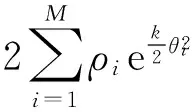
(18)

(19)

(18)式及(19)式中：ε即为多径传播条件下-3dB门限法测角的脉冲前后沿误差均值，单位为(BW)，故测角误差为Δθ=2ε。若略去fmax条件则(19)式变为

(20)

(20)式与(19)式在形式上不一样，且精度也不同，将在仿真实验中进行比较。

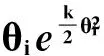
3精度分析

(19)式的推导过程中使用了许多近似等价式，近似等价会带来误差，该误差大小决定了(19)式的精确程度，现分析近似等价误差与(19)式的内在联系。

以(14)式作为精度分析的依据，对(15)式取微分得

(21)

(21)式中，Δfmax为fmax的计算误差。结合(15)式、(18)式可得

(22)

根据包络定理(见附录)不难得到脉冲前后沿误差的误差主要取决于峰值误差，故(21)式成立，并进一步可得

(23)

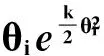
4仿真结果及分析

在量化分析方法的推导过程中使用了近似替代，在数学中其成立条件较为苛刻，但是在工程实践中只要其误差在一个较小的范围内，这种近似替代是成立的。现通过仿真实验，研究假设条件的正确性和误差量化公式的精度。

图3　MLS扫描脉冲与高斯脉冲对比图Fig.3　MLS scanning pulse and gaussian pulse contrast figure

其次，考察多径效应对脉冲峰值位置的影响。条件1：假设存在M=5条多路径，且{ρi}={0.06,0.061,0.062,0.063,0.061}，{θi}={0.5,0.53,0.54,0.52,0.49}，{δi}={0}，则直达信号包络和混叠信号包络峰值位置如图4所示。

图4　脉冲峰值变化示意图Fig.4　Sketch the pulse peak position

图4中混叠信号的峰值位置与直达信号峰值位置相差Δθ=0.080 0，理论计算值θp=0.073 3，两者非常接近，同时峰值误差Δfmax=0.017 1，非常微小，表明以f(0)替代fmax是可行的。

以上两方面的仿真结果表明量化分析方法的假设前提是成立的。

现考察(19)式的精度。试验条件2：假设存在M=5条多路径，且{ρi}={0.109,0.117,0.149,0.118,0.103}，{θi}={0.74,0.9,0.84,0.72,0.79}，{δi}={0}，仿真结果如表1所示。

表1　仿真结果对比

表1中混叠信号实际误差与理论误差一致，存在较小误差，其原因是由于在(19)式推导过程中使用的近似替代存在误差导致最终的结果有偏差，其误差范围较小，可以接受。对于场地效应引起的测角误差，需要考虑许多因素，其中多径效应是其中最主要的因素，因此(19)式的量化分析结果可以表征场地效应对MLS制导精度的影响，同时该方法忽略了一些因素，故存在一定误差，但对场地鉴定评估结果影响不大，因此该方法可以实现对场地鉴定的有效评估。

图5a及图5b所示为ρi值确定时，偏差与θi的关系；图5c及图5d所示为θi值确定时，偏差与ρi的关系。改进方法和原方法的精度归一化偏差变化趋势一致，同条件下，改进方法的偏差更小，表明该方法具有更高的精度。

5总结

本文面向量化场地效应问题，指出量化多径效应可以表征场地效应对MLS制导精度的影响程度，并针对量化多径效应引起脉冲定时点误差问题，推导了改进的MLS测角误差量化分析公式，并给出了该公式的量化精度，通过实验仿真，验证了推导中引入的假设条件的正确性；实验表明多径效应对脉冲峰值影响较小，量化分析过程中使用的近似替代成立。通过实验仿真验证了改进后的量化分析公式在精度上有所提高，表明该方法可以定量评估场地效应，在后续研究中将继续寻找更为精确的量化分析方法用以提高场地鉴定的可信度。

图5　精度对比图Fig.5　Accuracy comparison chart

参考文献：

[1]ICAO. Annex 10 to the convention on International Civil Aviation[S]. Montreal Canada: ICAO, 2006.

[2]ICAO.Internation Standard and Recommended Practices[S].Annex 10,VOL.I,Part I-Equiment and systems，Montreal Canada: ICAO, 2006. 1999，156-168.

[3]MATHIAS S A. Development of siting criteria for the collocation of the microwave landing system (MLS) and the approach lighting system (ALS)[D]. Ohio: Ohio University, 1988.

[4]QUINET D, ODUNAIYA S. Localizer receiver proximity and capture[C]∥Proceedings of IEEE 26th Digital Avionics System Conference. Dallas, Texas: IEEE, 2007: 4.C.2.1-4.C.2.8.

[5]ODUNAIYA S, QUINET D. Calculations and analysis of signal processing by various navigation receiver architectures[C]∥Proceedings of IEEE the 2004 Digital Avionics System Conference. Salt Lake City, UT: IEEE, 2004: 1.D.1-11-13.

[6]戴传金,吴德伟,卢艳娥,等.一种多径条件下的MLS接收机测角误差分析新方法[J].航空学报,2010,31(5):983-988.

DAI Chuanjin, WU Dewei, LU Yan’e,et al. A New Method of Angle Error Analysis of Microwave Landing System (MLS) Receiver Under Multipath Conditio[J].ACTA AERONAUTICA ET ASTRONAUTICA SINICA,2010,31(5):983-988.

[7]戴传金,吴德伟,赵修斌,等.微波着陆引导系统多径效应的数字仿真[J].北京邮电大学学报,2009,32(6):47-52.

DAI Chuanjin,WU Dewei,ZHAO Xiubin,et al.Research on Numerical Simulation of the Multi-path Effects on Microwave Landing System[J].Journal of Beijing University of Posts and Telecommunications, 2009,32(6):47-52.

[8]戴传金,吴德伟,赵修斌,等.微波着陆系统扫描波束主瓣替代的误差分析法[J].北京邮电大学学报,2012,35(2):28-31. DAI Chuanjin,WU Dewei,ZHAO Xiubin,et al.The Analysis Method of Error of MLS Based on Replacement Technology of Main-Lobe Beaming[J].Journal of Beijing University of Posts and Telecommunications,2012,35(2):28-31.

[9]周其焕,魏雄志.微波着陆系统[M].北京.国防工业出版社,1989:77-79.

ZHOU Qihuan,WEI Xiongzhi. Microwave Landing System[M].Beijing:National Defence Industrial press,1989:77-79.

附录：

包络定理(envelope theorem)

包络定理是比较静态研究的有用工具，记最优化问题：

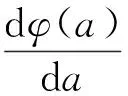
证明：

记对应参数值a的最大值为x(a)，假设它关于a可微，则有：

由于x(a)是上述最大化问题的解，所以一阶条件成立：

因此，包络定理得证，不难看出，最小化问题依然。

For site identification MLS pulse timing point measurementerror of quantitative analysis method

TANG Mao1, LI Xiaoming2, LI Chengfeng3, DENG Lixiang1

(1. Pelple’s Liberation Army 94683, Jinjian 362200, P.R. China; 2. School of Information and Navigation，Air Force Engineering University，Xi’an 710077，P.R.China； 3. People’s Liberation Army 94857， Wuhu 241000，P.R.China)

Abstract:In view of the multipath effect caused by MLS(microwave landing system) signal envelope distortion pulse timing point measurement error problem, an improved method for quantitative analysis of the error is put forward. Through analyzing the error of quantitative analysis of the process, the key factor to the error is pointed out, and according to the signal in the form of assumptions, the simplified model is put forward, the quantitative analysis of the error of the revised formula is derived, and the analysis formula of accuracy is analyzed as well. Simulation results show that the method can quantitatively analyse pulse timing point measurement error caused by the multipath effect, and realize the quantitative assessment of the appraisal.

Keywords：microwave landing system; multipath effect; timing point error; quantitative analysis

DOI：10.3979/j.issn.1673-825X.2016.03.006

收稿日期：2015-05-08

修订日期：2016-04-09通讯作者：唐茂296441191@qq.com

基金项目：国家自然科学基金(61273049)

Foundation Item：The National Natural Science Foundation of China(61273049)

中图分类号：TN961

文献标志码：A

文章编号：1673-825X(2016)03-0319-06

作者简介：

唐茂(1990-)，男，四川内江人，研究生，主要研究方向为军用无线电导航。E-mail：296441191@qq.com

(编辑：张诚)