高中数学探究式教学的实践研究

◇　江苏　张琰琰

高中数学探究式教学的实践研究

◇江苏张琰琰

高中数学教学不仅需要让学生掌握基本的理论知识、提高学生的考试成绩,更为重要的是培养学生的数学思维和数学思想,强化创新意识．素质教育时代背景下,高中数学教学重视提高学生自主学习能力、增强合作探究能力的培养．因此数学教师的首要任务是采取有效策略,培养学生的发散性思维,增强其计算能力和逻辑思维能力．

1创设适宜的问题情境,培养分析问题能力

问题是学生开展探究性学习的基础,是教师实施探究式教学的关键.教师根据学生的基础和学习发展目标,将教学内容转化为一定的问题情境，以此激活学生的思维,引导学生根据问题进行自主学习合作探究,围绕问题任务寻找知识间的相互联系,探究已知条件和未知结果之间的关系,寻找更多、更好的解决方法,提高学生的分析和探究问题能力．教师创设的问题可以基于对数学概念和定理的认识理解;可以利用学生已有的认知矛盾引发思维冲突;可以根据教材安排的先定理后应用程序进行转换,由一些常见的应用现象引出相应的定理依据,实施“问题预设—建构模型—解决问题—迁移能力”的探究式学习过程．

例如学习椭圆时,教材对中心不在原点的椭圆方程介绍非常少,但是对椭圆的第2定义和点到直线的距离公式分析得非常详细,如果教师能够把它们更好地融合在一起设置问题情境，供学生探究,就会收到意想不到的效果．

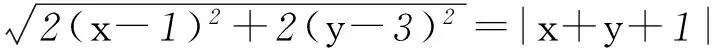
求点P(x、y)所对应的点的轨迹．

2鼓励学生合作交流,丰富情感体验

探究式教学是一种教学模式,是培养学生综合能力的重要方式．学生的探究能力必须在实践中获取,学生的综合素养需要在交流中不断丰富,学生对各种知识和方法的感悟需要在具体体验中生成．实施探究式教学一定要注重对学生的鼓励和引导,帮助学生在合作交流中体验．探究式教学过程中,需要学生提出自己的观点、表达自己的想法、分析自己的思路,并有理有据地维护自己的立场，需要倾听、理解或者反驳对方的思路,在争论和探讨中不断拓展思路、发散思维．学生在证明与反驳中强化认识、加深理解、锻炼思维,不断强化自信、学会分享、学会理解和支持．为此, 教师需要营造和谐、民主、轻松活跃的课堂气氛,让学生能够积极参与、勇于探究,获得实实在在的感悟和经验．

例如学习“圆锥曲线及其性质”时,可以从圆锥曲线的第2定义分析入手,引导学生探究椭圆、双曲线、抛物线的标准方程,再由方程全面地分析其性质．

(a2=b2+c2)；

(c2=a2+b2). 然后再通过几何画板画出其轨迹,学生能够很好地感知其轨迹是椭圆或双曲线．

此时,再进一步引导学生探究,如果现在给定一个条件a=c,就会发现此时的点F刚好就在直线l上,为此可以设定F(p/2,0)是直线x=-p/2外的一点,若点P到点F的距离等于到直线l的距离,再来探究点P的轨迹方程．进一步探究,能够得到点P的轨迹方程为y2=2px,再进一步研究其轨迹方程．

这样,在研究了圆锥曲线的方程和图象以后,进一步引导学生根据方程来研究其性质,分析椭圆和双曲线上的点到2个焦点距离的和或差的绝对值,再进一步分析直线和这些曲线的位置关系．这样的探究式教学活动能够让学生更好地感知概念、定理、公式、图象等.由一个知识点引导学生寻找问题的线索,在探究实践中获得真切的感受,真正掌握椭圆、双曲线等定义和性质．

3密切联系实际,增强实际问题解决能力

高中数学实施探究式教学,需要注重与现实生活、生产的密切联系,让学生能够结合实践分析数学现象、探究数学的应用价值,找到解决各种问题的办法,提高学生的应用实践能力．为此,教师需要挖掘数学与生产生活以及其他学科间的相互联系,培养学生观察、分析、建模等思维能力,树立良好的学科观,真正贯彻素质教育,培养全面发展的高素质人才．

图1　　　　　　　　　　图2

总之,高中数学教学不仅要让学生掌握基本的知识和定理,还应重点培养学生的综合素养、强化探索意识、增强探究能力,让学生能够真正做到会学习、会发现、会创新,从而培养出高素质人才．

(作者单位：江苏启东大江中学)