分子动力学模拟剪切速度对纳米间隙中角鲨烷界面滑移的影响

潘伶，高诚辉（福州大学机械工程及自动化学院，福建 福州 350108）



分子动力学模拟剪切速度对纳米间隙中角鲨烷界面滑移的影响

潘伶，高诚辉
（福州大学机械工程及自动化学院，福建 福州 350108）

摘要：采用聚合物一致性力场（PCFF），分别在7种剪切速度V和3种油膜厚度h下对纳米间隙中润滑剂角鲨烷进行分子动力学模拟，分析固液界面的密度、分子和流速的分布，探究纳米薄膜润滑的润滑机理和剪切速度对界面滑移的影响。结果表明，纳米间隙中润滑剂存在分层现象，各层间距相近，并非越远离固体壁面层间距越大，层间距约为角鲨烷分子单个C C键距离的3～4倍；随着油膜厚度的减小，纳米间隙中润滑剂层状分布越明显，固化层密度越大；当油膜厚度为3.44 nm时，固液界面滑移现象明显，滑移长度b值随着V先增大后减小，当V 为22.8 m·s-1时，b达到最大值4.35 nm；根据模拟和计算结果，给出滑移长度与剪切速度的关系公式。

关键词：分子模拟；纳米结构；聚合物；界面滑移；薄膜润滑；角鲨烷

2015-06-01收到初稿，2015-09-10收到修改稿。

联系人：高诚辉。第一作者：潘伶（1969—），女，博士，副教授。

Received date: 2015-06-01.

Foundation item: supported by the National Natural Science Foundation of China (51175085)，the Tribology Science Found of State Key Laboratory of Tribology (SKLTKF13A09) and the Natural Science Foundation of Fujian Province (2016J01226).

引　言

无滑移边界条件是经典流体力学和润滑理论中的重要假设，广泛应用于流体的理论分析、实验和实际工程。然而，近年来的研究发现界面滑移在许多情况下有可能发生，特别是存在于微纳米尺度下的流体。界面滑移的相关研究方法主要有理论数值分析、实验和分子动力学（MD）模拟。理论数值分析的物理模型主要有线性滑移长度模型[1]、极限剪应力模型[2-3]和非线性滑移长度模型[4-5]。实验方法常用的有原子力显微镜（AFM）[6]和表面力仪（SFA）[7]等。AFM方法是通过探针测量挤压流中流体阻力和膜厚的关系，再根据理论公式分析计算测量结果，而界面滑移的理论和数值分析还不完善。

目前，纳米薄膜润滑的研究仍处于初级阶段，其润滑机理、数学模型、微观分子分布和油膜厚度等的理论分析、模拟计算和实验检测都与工程实际有较大差距。对薄膜润滑进行深入研究并开发相应的实际应用技术有着重要的意义。随着计算机计算能力、并行技术以及相关势函数的发展，分子动力学模拟方法应用日益广泛[8-11]。采用MD模拟纳米间隙润滑剂，可以动态适时地显示全油膜中分子和密度的分布规律，克服了实物实验无法测量高速加载时润滑薄膜的密度和原子运动的缺点。另外，实验的方法不能检测新型的尚未研制出来的润滑剂，而MD方法则可以灵活准确地建立各种分子结构模型。

虽然在过去的20年里，纳米流体的界面滑移和薄膜润滑机理是研究的热点，但以往的研究，无论是实验、MD模拟还是数值分析的结论多数是建立在较为简化的模型和推理上[12-20]。以往的MD研究多数采用简单的单粒子硬球模型[5,21-23]，简单的LJ势函数描述分子间的相互作用[5,21-22,24]，或通过改变某一参数来模拟不同的湿润性、固液相互作用势和硬度等[22-23]对界面滑移的影响，而很少涉及液体的具体分子组成、结构和更为准确的分子力场。

本文采用聚合物一致性力场（PCFF）模拟研究纳米间隙内角鲨烷在固体壁面不同的剪切速度和油膜厚度下的分子、密度及流速分布，探究纳米间隙中固液界面的界面滑移及润滑机理。

1　模型的建立

图1是纳米间隙润滑剂剪切模型，纳米级角鲨烷润滑膜受限于两平行的固体壁面。图中球形表示原子，橙色球表示铝Al原子，蓝色球表示碳（C）原子，绿色球表示氢（H）原子。固体壁面采用面心立方fcc晶体铝Al(001)晶面，因为Al原子的Lennard-Jones势函数中的能量参数e=3.32320 kcal·mol-1（1 cal=4.1868 J），距离参数s=2.9964Å（1 Å=0.1 nm），其能量参数比Pt和Fe等原子小，固液之间的相互作用势较小，使得常压下界面滑移现象比较明显，而且Al也是常用的金属材料。在保证计算误差小于3%的情况下，为减少计算机集群的计算量，取Al晶体表面尺寸为6.48 nm×4.05 nm，晶格常数为0.405 nm。上、下固体壁面施加同样大小的反向速度V，V分别取7种介于3～30 m·s-1不同的速度。常压下油膜厚度h分别取3.44、5.13 和7.02 nm。

图1　不同剪切速度下纳米间隙润滑剂模型Fig.1　Model of confined thin film at different shear velocities

当h=3.44 nm时，模型中总共有13408个原子，其中有3840个Al原子、3120个C原子和6448个H原子，即润滑剂中共有104个角鲨烷分子；当h=5.13 nm时，模型中总共有18100个原子，润滑剂中共有155个角鲨烷分子；当h=7.02 nm时，模型中总共有23344个原子，润滑剂中共有212个角鲨烷分子。

常用于美容产品和医药保健品的角鲨烷，还可以作为电接触或机械接触润滑油的基础油，无毒且生物降解性高，是良好的环境友好润滑剂。角鲨烷的分子式为C30H62，分子结构和模型如图2所示。

2　模拟方法

采用大规模原子/分子并行模拟器（large-scale atomic/molecular massively parallel simulator，LAMMPS[25]）编程模拟纳米间隙润滑剂的剪切流动，分子力场采用聚合物一致性力场（polymerconsistent force field，PCFF），其力场参数是由大量的实验数据和精确的量子计算结果拟合得出，因此计算量大，模拟也更准确，适用于计算聚合物、有机物和生物分子体系，并含有一些金属原子的力场参数。 PCFF势函数包含非键结作用项、键伸缩项、键角弯曲项、二面角扭曲项、离平面振动项和多种交叉作用项，其势函数和各参数的选取详见文献[25-28]。

模型中油膜厚度方向即z方向采用自由边界条件，其他两个方向都设置成周期性边界条件。由于界面滑移受上、下固体壁面的变形影响较大，故将固体壁面设置成弹性可变形，壁厚为1.21 nm。非键结作用项中的LJ势作用项和库仑作用项的截断半径都取12.5 Å，因为当油膜厚度为5.31 nm时，其计算结果与截断半径取16 Å时非常接近，误差小于0.5%，但在美国SUN公司的Blade60000刀片服务器上单节点的计算时间可减少近1/3。分子动力学模拟时间步长取1 fs。采用共轭梯度法，通过迭代调整原子的位置以减小模拟体系的能量，确定合理的初始位形，其中能量偏差取10-6kcal·mol-1，力偏差取10-8kcal·(mol·Å)-1。先在微正则系综（NVE）下对模拟体系进行0.5 ns的弛豫以达到293 K恒温条件下的平衡。然后，在上、下固体壁面分别施加7种x向的方向相反的速度V，使纳米间隙中润滑剂受到1.8 ns的剪切作用。

图2　角鲨烷分子Fig.2　Squalane molecule

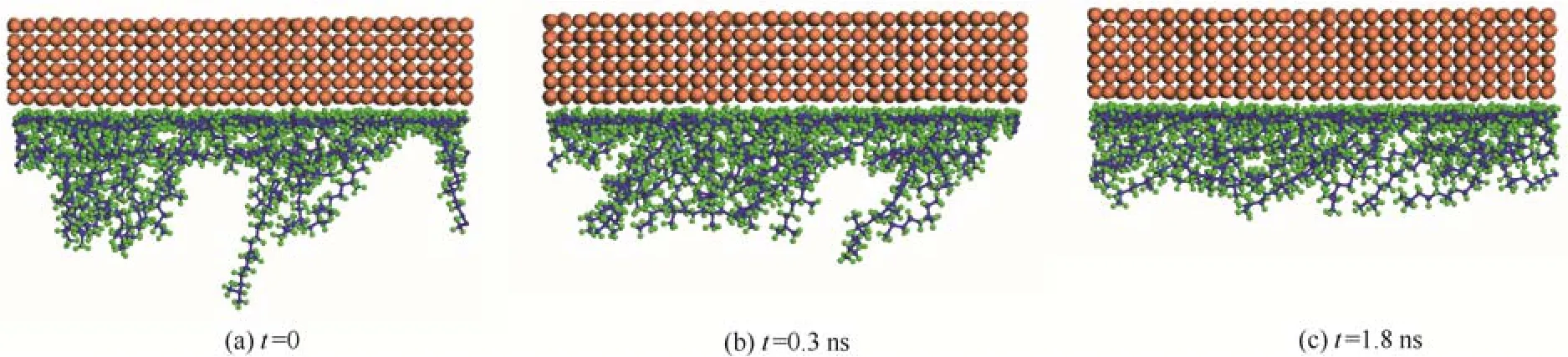
图3　h=7.02 nm、V=15 m·s-1时吸附层分子Fig.3　Distributions of squalane molecules adjacent to the wall at h=7.02 nm and V=15 m·s-1

根据模拟结果，采用简单实用的线性滑移长度模型计算滑移长度。线性滑移长度模型[1]认为固液交界处流体与固体的相对速度即滑移速度vs与流体在壁面的剪切速率g呈正比[29]

式中，b为滑移长度，表示固液界面滑移的程度；vx是流体沿x方向的流动速度。

3　结果与讨论

3.1润滑剂分子和密度的分布

图3是h=7.02 nm、V=15 m·s-1时，上固体壁面和角鲨烷吸附膜分子在不同剪切瞬时t的分布。由图可见，开始剪切时即t=0时，有较多的润滑剂分子接近垂直于固体表面分布，且跨越2～3层以上的润滑剂聚集层。随着剪切时间的增长，这些接近垂直分布的润滑剂分子出现弯曲和扭转，并与固体表面形成较小的角度或长分子链中的一部分与固体表面平行。

然而，以往的研究多数认为流体分子在近壁面处主要是平行于壁面，距离壁面越远的分子越垂直于壁面[12,30-31]。以往的研究多采用Legendre多项式表示的方向参数S( z )

式中，z是粒子质心的z坐标，θ是键方向与z轴的夹角。当键平行固体壁面时，q=90°，S( z )=-0.5；当键垂直于固体壁面时，q=0°，S( z )= 1。键的方向是取两相邻成键原子之间的键的方向[12,30]，或取几个连续成键原子中某两个原子中心的连线方向[31]，或以分子中功能基团定位，通过统计各区域的平均S( z )值来判断分子的方向。方向参数S( z )只能表明分子中部分键的方向，适于研究短链分子的方向，而长链分子在运动过程中普遍出现多次弯曲和扭转等，故S( z )不宜用于判断长链分子的方向。

当剪切时间t=1.8 ns时，将模拟体系沿z方向的总尺寸L（图1）分为200等分，以各原子中心所在位置为各原子的质心，计算出各等分中润滑剂的平均密度，并画出密度分布曲线，如图4(a)、(c)、(e)所示。由图可见，3种油膜厚度下，由于受到固壁的约束，在固液交界处都有一层密度很大的润滑剂层，即出现固化现象。油膜厚度越小固化层密度越大，固化层对界面滑移的影响也越大。

图4　沿油膜厚度方向角鲨烷质量密度和部分分子的分布Fig.4　Density and molecular distributions of lubricants in the z direction

当h=3.44 nm时，纳米间隙内润滑剂明显为层状分布并分为7层，如图4(a)所示，图中标出了各层之间的相对距离，可以看出各层之间距离没有明显的规律，而以往其他学者的研究常认为离壁面越远层间距越大[12-14]。实际上，在文献[32-33]中，采用原子力显微镜（AFM）测量探针在趋近润滑剂中的基片时所受的阻力，仔细观察文中的图就可以发现力曲线的层间距是不规则的，相同的现象在采用MD模拟的文献[34]的图中也可以观察到。当h=5.13 nm时，上、下固液交界处附近分别有明显的3～4层润滑剂，膜厚中部波动较小，如图4(c)所示，同样并非离壁面越远层间距越大；随着油膜厚度的增加，润滑剂分层现象越来越不明显。当h=7.02 nm时，只在上、下固液交界处附近有较明显的3～4层润滑剂，膜厚中部波动更小且无规则。另外，3种油膜厚度下，固体壁面附近的润滑剂层间距基本相等，约为0.507 nm。角鲨烷分子单个键的距离约为0.154 nm，各润滑剂聚集层中心间距离约为角鲨烷分子单个键距离的3～4倍。图4(b)、(d)、(f)是用不同的颜色表示随机抽取的少量分子，以清楚地显示润滑剂分子在纳米间隙中的分布，由图可见，同一分子常常跨越多层，而且出现弯曲和扭转。

以往的多数MD研究采用单粒子硬球模型，结果显示在垂直于油膜厚度方向（即xy平面），润滑剂分子在固液交界处呈有序化排列，x向密度分布呈周期性变化[13,19]。然而，研究结果显示，虽然纳米薄膜润滑中，z方向即沿油膜厚度方向润滑剂分层现象明显，但x方向没有分层的现象。图5是固液交界处xy平面上部分角鲨烷的分子分布。图6是角鲨烷在x方向密度分布曲线，可见曲线波动小，密度分布均匀，不存在周期性变化规律。

图5　固液交界面角鲨烷部分分子的分布Fig.5　Molecular distribution of squalane at solid- liquid interface

图6　x向角鲨烷质量密度分布Fig.6　Density profile of squalane in x direction

3.2界面滑移

当h=3.44 nm时，将整个模拟体系沿z方向分成34等分，图7是当V=10 m·s-1时，整个模拟体系沿x方向的速度分布。每个数据点的横坐标表示每等分中心的z坐标在整个体系中的相对位置；纵坐标表示每等分中原子x方向的平均速度。图7中上、下两条水平数据点分别表示上、下两固体壁面的速度；中间的数据点是角鲨烷流体的速度分布。由图可见，固液交界处有明显的相对速度即出现界面滑移，润滑剂流速vx呈非线性分布。固体壁面的速度V与流体在固液交界处的速度vx之差即为滑移速度vs，图中流体速度分布曲线在固液交界处的变化率除以L即为剪切速率g。

图7　V=10 m·s-1时x向速度分布Fig.7　Velocity in x direction at V=10 m·s-1

图8是h=3.44 nm、V=10 m·s-1时流体在3个方向的分段平均流速vx、vy和vz分布。与vx相比，vy和vz变化很小，特别是vz变化更小，说明在宏观上流体属于层流。图8中的插图是放大的vz分布图，可以看出，在靠近固液交界处vz几乎为0，而油膜中心附近vz稍大。

图8　V=10 m·s-1时角鲨烷3个方向的速度分布Fig.8　Velocity in three directions at V=10 m·s-1

在固体壁面上分别施加7种不同的速度V，并取流体上半部分（z/L≥0.5）进行分析，如图9所示。由图可见，当V=3～30 m·s-1时，固液交界处的流体速度vx和速度变化率随着V的增大而增大；当V=25 m·s-1后，固液交界处的速度变化率明显增大；同时，随着V的增大，流体速度vx呈非线性分布越明显。

图9　不同V时纳米间隙上半部分流体的速度分布Fig.9　Velocities of upper fluids at different shear velocities

图10(a)、(b)中的离散数据点分别是根据图9的数据计算出的固液界面的相对速度vs和剪切速率g，图中曲线分别是对离散点进行线性和3次多项式拟合后的曲线。图10(c)中的离散数据点是根据图10(a)、(b)中的离散数据点，由线性滑移长度模型的式（1）计算得出的滑移长度b，图中曲线是二次多项式拟合曲线，其表达式为

式（3）方便地表达了滑移长度b与剪切速度V的关系。由图10可以看出，随着V的增大，vs值基本呈线性增大，剪切速率g呈非线性增大且在V＞20 m·s-1后增大更明显，从而使得滑移长度b值随着V先增大后减小。当V=22.8 m·s-1时，b达最大值4.35 nm。

4　结　论

在PCFF力场下，采用MD方法模拟不同剪切速度下纳米间隙角鲨烷的剪切流动。分析了流体分子、密度和流速的分布，计算出固液界面的滑移长度，得出以下结论。

（1）固液交界处液体分子形态各异，长链分子中的部分平行于固体壁面，部分垂直于固壁，还有部分与固壁呈一定角度。方向参数S(z)不宜作为长链分子方向的判定依据。

（2）各种油膜厚度下，在固体壁面附近，都有一层密度很大的润滑剂固化层。随着油膜厚度的减小，纳米间隙中润滑剂层状分布越明显，固化层密度越大，固化层对界面滑移的影响也越大。层间距基本相等，并非离壁面越远层间距越大。层间距约为角鲨烷分子单个C C键距离的3～4倍。

图10　各参数随V的变化Fig.10　Factors as functions of shear velocity

（3）由于Al和squalane原子之间相互作用势较小时，在常压下就出现界面滑移现象。当油膜厚度为3.44 nm时，随着剪切速度V的增大，流速vx明显呈非线性分布，固液交界处的相对速度vs基本呈线性增大，剪切速率g呈非线性增大且在V＞20 m·s-1后增大更明显，从而使得滑移长度b值随着V先增大后减小。根据模拟和计算结果，给出了滑移长度与剪切速度的关系公式。

本文的研究克服了实物实验无法测量纳米间隙中流体的密度及分子运动规律等的缺点，为采用分子动力学方法定量地、动态适时地预测纳米间隙流体的密度和分子分布，进一步探究纳米薄膜润滑机理、研究应用界面滑移和开发新型润滑剂提供了可靠的依据。

符号说明

b ——滑移长度，nm

h ——油膜厚度，nm

L ——模拟体系沿z向的总尺寸，nm

t ——剪切时间，ns

V ——剪切速度，m·s-1

vs——滑移速度，m·s-1vx，vy，vz——分别为流体在x、y和z方向的分速度，

m·s-1

g——剪切速率，ns-1

ε ——能量参数，kcal·mol-1

ρ ——密度，kg·m-3

σ ——距离参数，Å

References

[1] OLDSTEIN S. Modern Developments in Fluid Dynamics [M]. Vol Ⅱ. Oxford: Clarendon Press，1957: 676-680.

[2] BEAVERS G S，JOSEPH D D. Boundary conditions at a naturally permeable wall [J]. Journal of Fluid Mechanics，1967，30 (1): 197-207. DOI: 10.1017/S0022112067001375

[3] MA G J，WU C W，ZHOU P. Wall slip and hydrodynamics of two-dimensional journal bearing [J]. Tribology International，2007，40: 1056-1066. DOI: 10.1016/j.triboint.2006.10.003.

[4] THOMPSON P A，TROIAN S M. A general boundary condition for liquid flow at solid surfaces [J]. Nature，1997，389: 360-362. DOI: 10.1038/38686.

[5]RIEZJEV N V，TROIAN S M. Molecular origin and dynamic behavior of slip in sheared polymer films [J]. Physical Review Letters，2004，92 (1): 018302. DOI: 10.1103/PhysRevLett.92.018302.

[6] JING D，BHUSHAN B. Boundary slip of superoleophilic，oleophobic，and superoleophobic surfaces immersed in deionized water，hexadecane，and ethylene glycol [J]. Langmuir，2013，29 (47): 14691-14700. DOI: 10.1021/la4030876.

[7] ESPINOSA-MARZAL R M，ARCIFA A，ROSSI A，et al. Microslips to “avalanches” in confined，molecular layers of ionic liquids [J]. The Journal of Physical Chemistry Letters，2013，5 (1): 179-184. DOI: 10.1021/jz402451v.

[8] 陈其乐，孔宪，卢滇楠，等. 外壁电荷性质对双壁碳纳米管中水分子运动行为的影响 [J]. 化工学报，2014，65 (1): 319-327. DOI: 10.3969/j.issn.0438-1157.2014.01.042. CHEN Q L，KONG X，LU D N，et al. Molecular simulation of outer surface charge on water transport through double-wall carbon nanotube [J]. CIESC Journal，2014，65 (1): 319-327. DOI: 10.3969/j.issn.0438-1157.2014.01.042.

[9] 张程宾，赵沐雯，陈永平，等. 流体密度对纳通道内流动滑移的影响 [J]. 化工学报，2012，63 (S1): 12-16. DOI: 10.3969/j.issn.0438-1157.2012.zl.003. ZHANG C B，ZHAO M W，CHEN Y P，et al. Effects of fluid density on velocity slip in nanochannels [J]. CIESC Journal，2012，63 (S1): 12-16. DOI: 10.3969/j.issn.0438-1157.2012.zl.003.

[10] 潘伶，高诚辉. 纳米间隙润滑剂季戊四醇四酯的压缩性能分子动力学模拟 [J]. 机械工程学报，2015，51 (5): 76-82. DOI: 10.3901/JME.2015.05.076. PAN L，GAO C H. Molecular dynamics simulation on the compressibility of pentaerythritol tetra in nanogap [J]. Journal of Mechanical Engineering，2015，51 (5): 76-82. DOI: 10.3901/JME.2015.05.076.

[11] PAN L，GAO C H. Confined fluid density of a pentaerythritol tetraheptanoate lubricant investigated using molecular dynamics simulation [J]. Fluid Phase Equilibria，2015，385: 212-218. DOI: 10.1016/j.fluid.2014.11.014.

[12] TSIGE M，PATNAIK S S. An all-atom simulation study of the ordering of liquid squalane near a solid surface [J]. Chemical Physics Letters，2008，457 (4/5/6): 357-361. DOI: 10.1016/j.cplett.2008.04.026.

[13] KARNIADAKIS G，BESKOK A，ALURU N. Microflows and Nanoflows: Fundamentals and Simulation [M]. Berlin Heidelberg，New York: Springer，2004: 1-23.

[14] PERTSIN A J，GRUNZE M. Long-ranged solvation forces in a fluid with short-ranged interactions [J]. Journal of Chemical Physics，2003，118 (17): 8004-8009. DOI: 10.1063/1.1564051.

[15] LOI S，SUN G，FRANZ V，et al. Rupture of molecular thin films observed in atomic force microscopy (II): Experiment [J]. Physical Review E，2002，66 (3): 031602. DOI: 10.1103/PhysRevE.66.031602.

[16] FRANZ V，BUTT H-J. Confined liquids:  solvation forces in liquid alcohols between solid surfaces [J]. The Journal of Physical Chemistry B，2002，106 (7): 1703-1708. DOI: 10.1021/jp012541w.

[17] 陈天星. 利用原子力显微镜对近壁面受限液体性质的研究 [D].北京: 清华大学，2011. CHEN T X. Study on properties of the confined liquids at solid surface with AFM[D]. Beijing: Tsinghua University，2011.

[18] SIVEBAEK I M，SAMOILOV V N，PERSSON B N J. Squeezing molecularly thin alkane lubrication films: layering transitions and wear [J]. Tribology Letters，2004，16 (3): 195-200. DOI: 10.1023/B:TRIL.0000009730.31175.82.

[19] 胡元中，王慧，郭炎. 超薄油膜润滑的分子动力学模拟 [J]. 摩擦学学报，1995，15 (2): 138-144. DOI: 10.16078/j.tribology.1995.02.007. HU Y Z，WANG H，GUO Y. Molecular dynamics simulation of ultra thin film lubrication (I): Rigid molecule model [J]. Tribology，1995，15 (2): 138-144. DOI: 10.16078/j.tribology.1995.02.007.

[20] 王慧，胡元中，郭炎. 超薄润滑膜界面滑移现象的分子动力学研究 [J]. 清华大学学报 (自然科学版)，2000，40 (4): 107-110. WANG H，HU Y Z，GUO Y. Molecular dynamics study of interfacial slip behavior of ultrathin lubricating films [J]. J. Tsinghua Univ. (Sci. & Tech.)，2000，40 (4): 107-110.

[21] NAGAYAMA G，CHENG P. Effects of interface wettability on microscale flow by molecular dynamic simulation [J]. International Journal of Heat and Mass Transfer，2004，47: 501-513. DOI: 10.1016/j.ijheatmasstransfer.2003.07.013.

[22] ASPROULIS N，DRIKAKIS D. Boundary slip dependency on surface stiffness [J]. Physical Review E，2010，81 (6): 061503. DOI: 10.1103/PhysRevE.81.061503.

[23] ZHANG H，ZHANG Z，YE H. Molecular dynamics-based prediction of boundary slip of fluids in nanochannels [J]. Microfluidics and Nanofluidics，2012，12 (1-4): 107-115. DOI: 10.1007/s10404-011-0853-y.

[24] NOORIAN H，TOGHRAIE D，AZIMIAN A R. Molecular dynamics simulation of poiseuille flow in a rough nano channel with checker surface roughnesses geometry [J]. Heat and Mass Transfer，2014，50 (1): 105-113. DOI: 10.1007/s00231-013-1232-x.

[25] PLIMPTON S. LAMMPS molecular dynamics simulator[EB/OL]. [2015-5-15]. http://lammps.sandia.gov.

[26] PLIMPTON S. Fast parallel algorithms for short-range molecular dynamics [J]. Journal of Computational Physics，1995，117 (1): 1-19. DOI: 10.1006/jcph.1995.1039.

[27] SUN H. Ab initio calculations and force field development for computer simulation of polysilanes [J]. Macromolecules，1995，28 (3): 701-712. DOI: 10.1021/ma00107a006.

[28] SUN H. COMPASS:  an ab initio force-field optimized for condensed-phase applications overview with details on alkane and benzene compounds [J]. Journal of Physical Chemistry B，1998，102 (38): 7338-7364. DOI: 10.1021/jp980939v.

[29] NAVIER C L M H. Memoire sur les du movement des fluids [J]. Mem l'Acad Roy Sci l’Inst France，1823，6: 389-440.

[30] VADAKKEPATT A，DONG Y，LICHTER S，et al. Effect of molecular structure on liquid slip [J]. Physical Review E，2011，84 (6): 066311. DOI: 10.1103/PhysRevE.84.066311.

[31] MENDONCA A C F，FOMIN Y D，MALFREYT P，et al. Novel ionic lubricants for amorphous carbon surfaces: molecular modeling of the structure and friction [J]. Soft Matter，2013，9 (44): 10606-10616. DOI: 10.1039/C3SM51689J.

[32] LIM R，O’SHEA S J. Solvation forces in branched molecular liquids [J]. Physical Review Letters，2002，88 (24): 246101. DOI: 10.1103/PhysRevLett.88.246101.

[33] LIM R，LI S F Y，O’SHEA S J. Solvation forces using sample-modulation atomic force microscopy [J]. Langmuir，2002，18 (16): 6116-6124. DOI: 10.1021/la011789+.

[34] ZHENG X，ZHU H，KOSASIH B，et al. A molecular dynamics simulation of boundary lubrication: the effect of n-alkanes chain length and normal load [J]. Wear，2013，301 (1/2): 62-69. DOI: 10.1016/j.wear.2013.01.052.

Molecular dynamics simulation of boundary slip in nanogap: effect of shear velocity

PAN Ling，GAO Chenghui
(School of Mechanical Engineering and Automation，Fuzhou University，Fuzhou 350108，Fujian，China)

Abstract:Molecular dynamics (MD) simulations using the polymer consistent force field (PCFF) were adopted to investigate the density，molecular and velocity distributions of lubricant squalane in nanogap at 293 K，three different film thicknesses and a wide range of shear velocities. The lubrication mechanism and boundary slip were analyzed. The results showed that the lubricant atoms tended to form layers parallel to the confining wall. The distances between the layers of lubricant atoms were irregular rather than broadening far away from the walls and were about three to four times the length of C C bond in the squalane. The tendency of lubricant atoms to form layers and the density of solid-like layer increased with decreasing film thickness. It was clearly to find the boundary slip at the solid-liquid interface from the velocity profile. The slip lengths increased with increasing velocity of substrates at the beginning，and then decreased. When the film thickness was 3.44 nm，the maximum slip length was 4.35 nm at the substrate velocity of 22.8 m·s-1. According to the simulations，the relationship between the slip length and the shear velocity was given.

Key words:molecular simulation; nanostructure; polymers; boundary slip; thin film lubrication; squalane

DOI：10.11949/j.issn.0438-1157.20150755

中图分类号：TH 117.2

文献标志码：A

文章编号：0438—1157（2016）04—1440—08

基金项目：国家自然科学基金项目（51175085）；清华大学摩擦学国家重点实验室开放基金项目（SKLTKF13A09）；福建省自然科学基金项目（2016J01226）。

Corresponding author:Prof. GAO Chenghui，gch@fzu.edu.cn