基于“同课异构”对数学课堂提问的研究
——以“椭圆的简单几何性质”为例
张春飞
山西师范大学教育科学研究院,山西 临汾 041000
基于“同课异构”对数学课堂提问的研究
——以“椭圆的简单几何性质”为例
张春飞* 1
山西师范大学教育科学研究院,山西临汾041000
摘要:解析几何的一个基本问题是由曲线方程研究曲线几何性质,“椭圆的简单几何性质”是学生第一次较为系统地学习在解析几何中如何用代数方法研究曲线性质。本文将以“椭圆的简单几何性质”为载体,就教师课堂提问特点,对三所中学的三位教师的课堂教学进行分析比较。
关键词:解析几何;椭圆;几何性质;课堂提问
2015年11月在山西省原平一中进行了“同课异构整体说课”教研活动。其中,自主课、展示课的讲课内容是人教A版普通高中课程标准实验教科书高中数学选修2-1第二章圆锥曲线第二节《椭圆的简单几何性质》。现对其中三所学校的课堂教学过程进行展现并分析。
一、自主课的呈现
(一)动手画,温旧知
上课前老师与班级学生对接,安排自主学习。在自习课上老师了解学生学情,让学生体会画椭圆的过程,回顾知识发生发展过程,为探究椭圆几何性质作铺垫,使学生经历数学知识的抽象过程。
(二)重知识生成,寻新旧联系
在自习过程中,老师及时指导学生要注重知识生成的过程,不能只注重结果。前面的知识是后面知识的基础,后面知识是前面知识的延续、深化与发展,引导学生学习新知识时寻找新旧知识的联系,将椭圆的几何性质与函数、三角函数联系起来,为学生架起由旧知通向新知的桥梁。
(三)拓知识,做准备
老师在自习课上拓展有关离心率的知识,学生通过PPT对新知识有一个初步感知。自习课结束时,每个小组都有任务,为明天的展示课做准备,最后老师将学生遗留的问题收回,对教案进行及时调整。
二、展示课的呈现
(一)A中学
第一组:讲解椭圆的几种作图方法
第二组:讲解椭圆方程中x、y的取值范围(从数、形两个角度考虑)
第三组:长轴长、短轴长、顶点坐标、长半轴长、短半轴长
老师提问:什么叫轴对称?什么叫中心对称?
老师矫正顶点的定义:椭圆与对称轴的交点
第七组:归纳焦点在x轴上的椭圆的简单几何性质,探索焦点在y轴上的椭圆,说说它有怎样的结合性质?结合图形列表归纳小结。
最后,老师和学生一起总结出a,b,c的关系、焦距、离心率、半轴长是椭圆的特有性质。整堂课通过7个问题的研究及小组展示老师总结,解决了互动卡上学生提出的共性问题。
(二)B中学类比深入,开始问动模式
问题1:若P为椭圆上的任一点,则P点横纵坐标的范围是____________。
通过小组同学观察、讨论,展示做题方法及结果,老师总结出同学们解决这道题通过图形的角度和数量的角度分析,都能很好的完成这道题。在全班交流的过程中,使大家了解到彼此思考问题的角度和做题思路,调动学生上课积极性。
问题2:O为坐标原点,P为椭圆上任意一点,|OP|的取值范围是____________。
小组代表展示,这道题有两种考虑角度:
第一种,从数的角度分析(函数的角度)
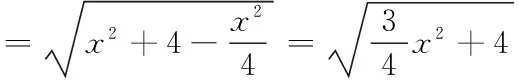
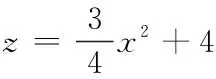
∴z∈[4,16]∴|OP|∈[2,4]
第二种,从图形的角度分析
以原点为圆心,半长轴、半短轴分别为半径作圆,观察分析图形即可得出结论。
老师对同学们的表现夸奖并进行归纳:
问题3:若P(x,y)点在椭圆上,还有哪些点在椭圆上?

问题4:任务一中A,B,C,D四点特殊吗?是椭圆的____________。
学生答:特殊,是椭圆的顶点。
老师问:那么椭圆顶点的定义是什么?
学生答:椭圆与对称轴的交点。
老师问:为什么说是椭圆与对称轴的交点?而不是椭圆与坐标轴的交点呢?
学生答:椭圆的对称轴会随椭圆的中心变化,当椭圆的中心是坐标原点时,它的对称轴才是坐标轴,所以必须考虑椭圆的中心在哪里。
问题5:在任务三中发现了什么?
离心率的概念:椭圆焦距与长轴长之比
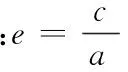
考察椭圆形状与e的关系:
当e→1,c→0,椭圆变圆,直至成为极限位置圆,此时可以认为圆为椭圆在e=0时的特例;
当e→1,c→a,椭圆变扁,直至成为极限位置线段F1F2,此时可认为线段为椭圆在e=1时的特例。
(三)C中学
问题3:如何求椭圆的顶点坐标,长轴、长轴长、短轴、短轴长分别是什么?
1.椭圆的离心率e的表达公式是什么?e的取值范围是多少?e的取值变化时椭圆的圆扁程度有什么变化?
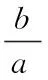
总结提升
用坐标法研究椭圆几何性质将复杂几何关系的研究转化为对曲线方程特点的考察,引导学生通过探究得到以下结论:
三、课堂教学提问分析
三位教师在教学过程中各类问题运用比例不尽相同,但从平均使用情况分析来看,教师最多运用的是“提示性问题”,“提示性问题”的使用说明教师善于根据学生回答问题的情况,来进一步提出相应的问题,启发学生进一步思考;同时教师较多运用的是“评价性问题”,“评价性问题”的使用说明教师很注重学生的判断思维,培养学生独立思考的能力;而老师使用相对较少的是“管理性提问”和“转换性提问”。一方面说明了学生在数学课中的课堂纪律比较好,另一方面,教师没有很好的将“数形结合思想”贯穿其中,数学符号与语言之间的转换不是很熟练,有待继续提升。
[参考文献]
[1]叶立军,周立芳.基于录像分析背景下的教师提问方式研究[J].教育理论与实践,2012(5).
[2]陆学政,刘清尧.人教A版“椭圆的简单几何性质”教材研读[J].中学数学教学,2013(3).
[3]陈淼君,沈文选.数学课堂中的提问[J].中学数学研究,2005.
*作者简介:张春飞(1995-),女,汉族,山西大同人,山西师范大学教育科学研究院学科数学专业硕士研究生。
中图分类号:G633.6;G635.1
文献标识码:A
文章编号:1006-0049-(2016)11-0087-02

