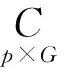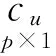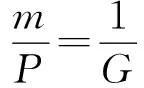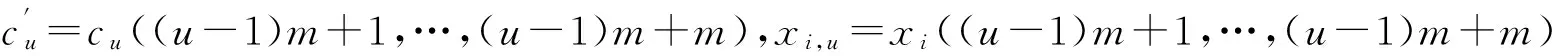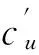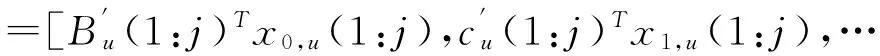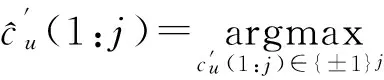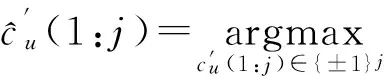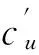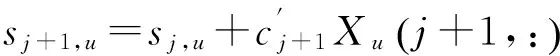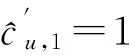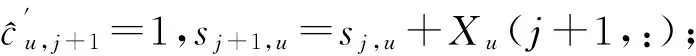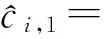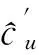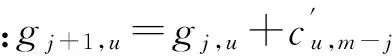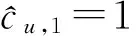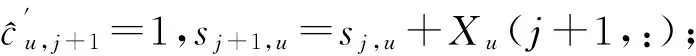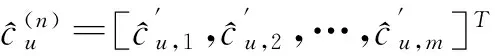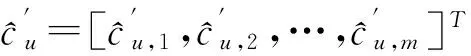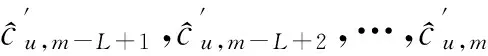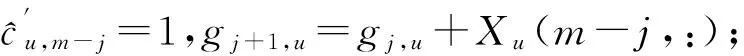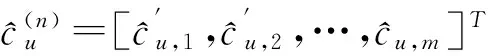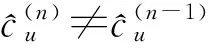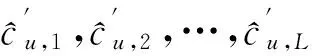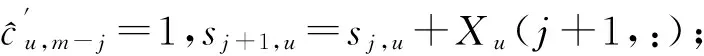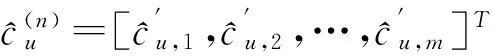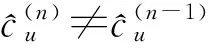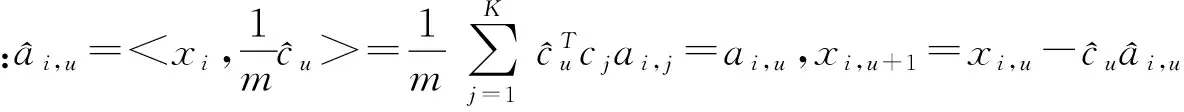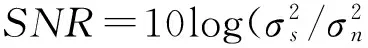周期长码直扩信号扩频序列的盲估计
王建雄 张立民 马 超
(1.海军航空工程学院电子信息工程系 烟台 264001)(2.海军航空工程学院融合所 烟台 264001)
周期长码直扩信号扩频序列的盲估计
王建雄1张立民2马超1
(1.海军航空工程学院电子信息工程系烟台264001)(2.海军航空工程学院融合所烟台264001)
摘要针对周期长码(PLC)直扩信号扩频序列的盲估计问题,提出了一种基于Viterbi算法的扩频码搜索算法。该算法首先将周期长码直扩信号等效建模为多用户短码直扩信号模型,将问题简化为短码直扩信号扩频码的估计;然后利用Viterbi算法实现扩频序列的估计;最后将估计出的所有虚拟用户的扩频序列相加得到所求的扩频码。理论分析和仿真结果表明,该算法能实现较低信噪比下的周期长码直扩信号扩频码的估计,并且运算量小。
关键词周期长码; 直接序列扩频; 扩频序列估计; Viterbi算法; 盲估计
Class NumberTN911
1引言
直接序列扩频技术是一种广泛应用于军事和民用领域的信息传输技术,它利用与待传输数据无关的序列对被传输信号进行频谱扩展,使其带宽远大于待传信息所要求的最小带宽。在电子对抗时代,扩频技术是强有力的电子对抗手段之一。在对抗通信中,实施相干干扰的首要条件是获得扩频序列。DSSS信号根据扩频周期与信息序列周期的关系,可以分为短码和长码。短码信号是指一个扩频周期只调制一位信息码,而长码信号一个扩频周期调制多位信息码。相较于短码信号而言,关于长码DSSS信号方面的研究较少。根据扩频周期与信息周期的比例关系可以将长码DSSS信号分为两种情况:当比例为整数时,将其定义为周期长码直扩信号[1];当比例为非整数时,将其定义为非周期长码直扩信号[1]。由于周期长码DSSS信号的形式较为简单,相关方面的研究较多。
在文献[2]中,M. K. Tsatsanis等曾提出,对于周期长码信号而言,可以通过将其等效为周期时变的信道来加以解决。文献[3]提出了一种新的求解信号协方差矩阵的方法,即先将信号经过码片延迟相乘,最后通过对该矩阵进行特征分解实现扩频序列的估计。文献[4]提出将周期长码直扩信号(PLC DSSS)等效为同步多用户短码直扩信号来求解。后来,白娟等人在文献[5]中提出将周期长码直扩信号等效为虚拟多用户短码直扩信号CDMA系统,该方法降低了对信号类型的限制,可以实现非同步信号的扩频序列估计。文献[6]采用针对最大似然估计问题,采用Viterbi算法实现了扩频序列的搜索,为直扩信号扩频序列的估计提供了新思路。文献[7]在虚拟多用户模型的基础上,建立了一种新的信号模型,并在此基础上采用Fast-ICA算法实现了周期长码直扩信号的盲同步和扩频码估计。文献[8]同样是将周期长码直扩信号建模为虚拟多用户模型,然后利用改进二阶统计盲辨识算法实现扩频序列的估计。
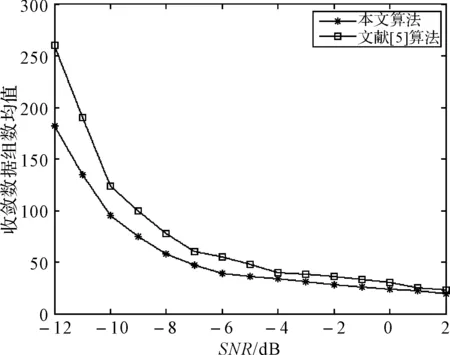
针对现有周期长码直扩信号扩频码估计算法计算量大的问题,本文在文献[4]的基础上进行扩展,实现了一种利用Viterbi算法对扩频序列的估计。本文所提算法与白娟[5]等相比,计算量更低,且易于硬件实现。
2信号模型
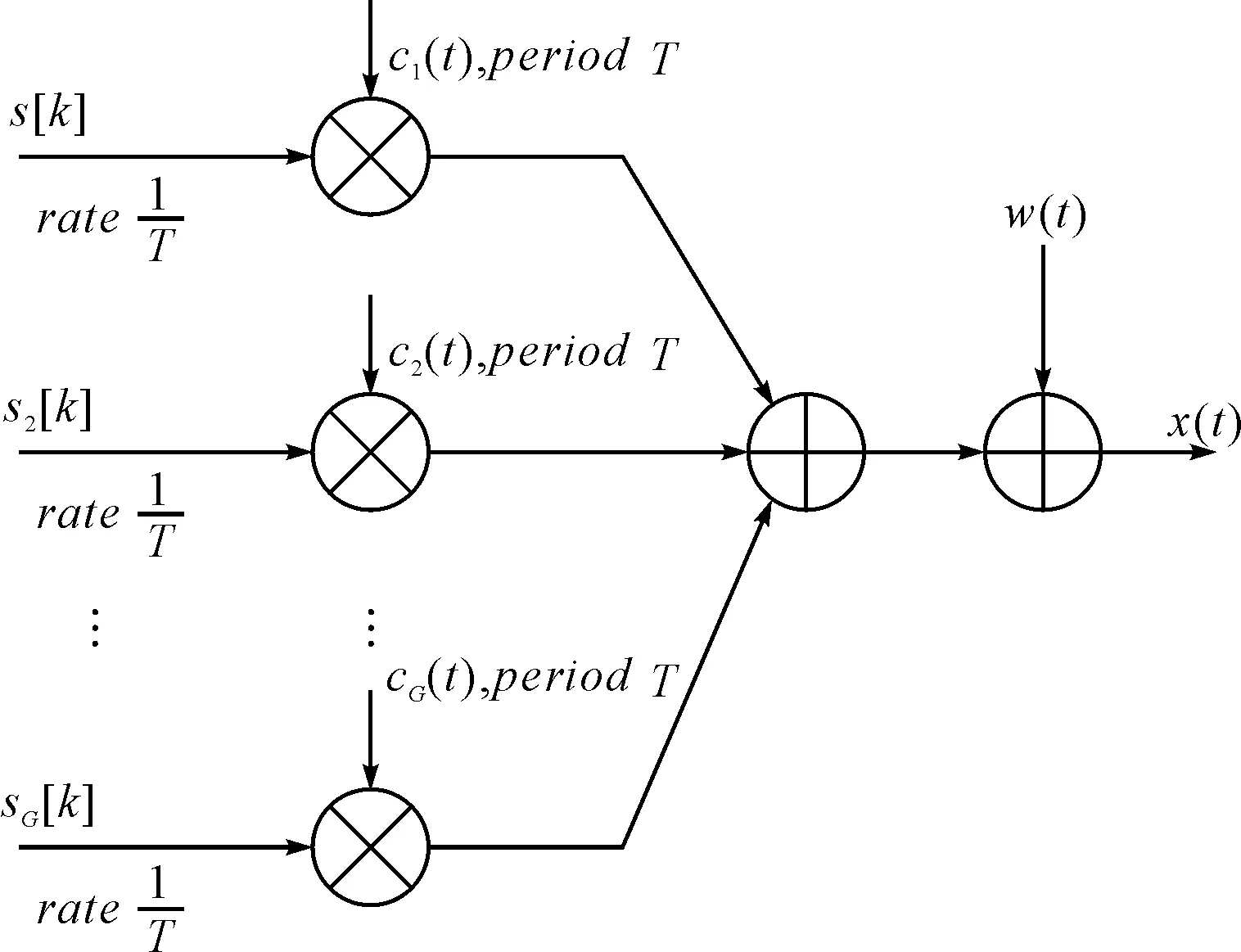
接收到的基带信号模型如图1所示。
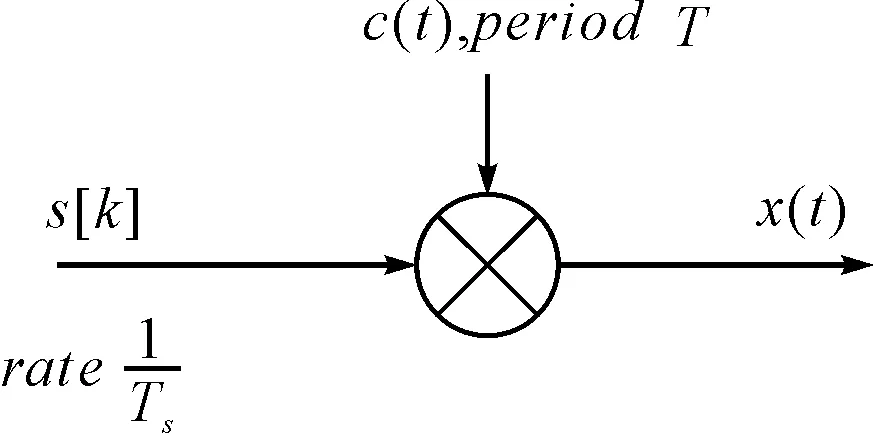
图1 周期长码直扩信号模型
其中c(t)是扩频码,Tc是码片周期。扩频码是周期序列,但又不同于短码,它的每个周期包含多个信息符号。假设周期为T的扩频码包含G个信息符号,其中G是整数,信息符号周期为Ts。
假设信息序列{s[k]}是独立同分布的,w(t)为高斯白噪声,且与信息序列无关。接收到的信号可以写为如下形式:
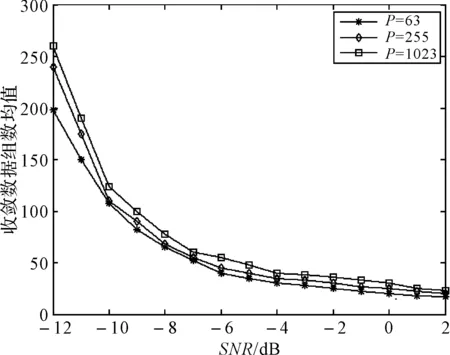
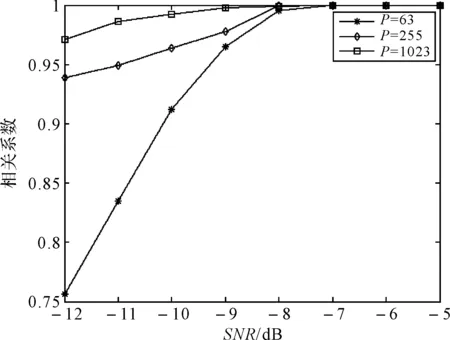
KT (1) 式中cu(t)的定义如下 cu(t) (2) su[k]s[Gk+u-1],u=1,…,G (3) 式(1)中的周期长码直扩信号可以等效认为是一个多用户系统,如图2所示。 图2 白噪声信道下周期长码直扩信号等效多用户模型 模型中包含G个虚拟用户。cu(t)为第u个用户的扩频码,码速率为1/T,u=1,…,G。这里将接收到的信号窗表示为采样数据,令采样间隔Δ=T/p。为了充分利用扩频序列的扩频增益,p至少要大于T/Tc。将采样信号表示为 x[n]x(nΔ),c[n]c(nΔ), cu[n]cu(nΔ),w[n]w(nΔ) (4) 因此可以将式(1)表示为过采样离散信号 n=0,…,p-1 (5) 可以把接收信号简写为如下形式 x[k]=C·s[k]+w(k) (6) 式中 x[k], w[k] (7) (8) cu,u=1,2,…,G是第u个虚拟用户的扩频序列,可以表示为 (9) 式中m=p/G,假设m为整数。 3算法原理 3.1基于Viterbi算法的扩频码搜索方法 假设扩频码的周期T已知,将接收信号式(1)按周期T划分成多个非重叠窗口。 用Q表示接收到的时间窗的个数,将第u个虚拟用户的采样数据记为Xu[x0,u,x1,u,…,xQ-1,u],则其似然模型表示如下 (10) 其中:j=1,2,…,m;det(·)表示对括号中的矩阵求行列式;Xu(1:j,:)表示矩阵Xu的第1行到第j行元素组成的矩阵。根据文献[9~10]可知,最大化似然函数可以等效为 (11) (12) (13) 记 sj,u 为1×Q维的行向量,则式(13)可以表示为 (14) 其中,‖·‖2表示向量的2-范数。由文献[11~12]可知,向量的2-范数与向量的1-范数是等价的,即对所有可能的有限维空间中的向量sj,u,分布按其向量2-范数与向量1-范数排序,排序结果不会因其范数的种类不同而不同。由矩阵分析可知,向量的1-范数的运算量要小于向量的2-范数的运算量,因此,本文将用向量的1-范数来进行运算。所以式(14)可以等效为 (15) 其中,‖·‖1表示向量的1-范数。定义如下度量值: D(j)‖ 由于扩频码cu∈[±1]m,对于式(14)、式(15)的求解可以考虑使用搜索的方法。当需要进行估计的扩频序列的位数为n时,最多需要进行2n次检测。因此,当扩频序列的位数n较大时,算法计算量太大。Viterbi算法可以用来减小算法的运算量。当度量值最大时,有两种情况:扩频码和它的反相序列。由此可知,在进行Viterbi译码搜索时,每次只需要计算2条路径的度量值,保存1条幸存路径。 基于Viterbi算法的短码直扩信号扩频码单向搜索算法的步骤如下: Step3j=j+1,如果j 3.2扩展到长码扩频序列估计 从式(9)中不难看出,各虚拟用户的扩频序列是相互正交的。下面将利用这一特点进行周期长码直扩信号扩频序列的盲估计。 由独立分量分析(Independent Component Analysis,ICA)可知,每个虚拟用户的扩频码可以通过投影追踪的方法来依次进行估计。 利用以上两式,可以从接收信号中剥离出第一个虚拟用户的信号。将yi作为接收信号,利用同样的方法可以估计出第2个虚拟用户的扩频码,重复以上过程,可以估计出所有虚拟用户的扩频码。最后将估计出的G个虚拟用户的扩频码进行相加,即可估计出所求扩频码。 定义gj,u为1×Q维的行向量。利用Viterbi算法反向搜索扩频码时的度量值E(j)的定义如下: E(j)‖gj,u‖1 基于Viterbi算法的短码直扩信号扩频码双向搜索算法的步骤如下: Step1令u=1,记xi,u=xi((u-1)m+1,…,(u-1)m+m),对第一个虚拟用户的扩频序列进行搜索。 Step2初始化Viterbi搜索次数M及扩频码保留位数L(1 Step5j=j+1,如果j Step10j=j+1,如果j Step15j=j+1,如果j Step19u=u+1,如果u≤G,返回Step2;否则,算法结束。将所求得的所有虚拟用户的扩频序列相加,得到一个完整长码周期的扩频序列。 4仿真分析 实验1:算法性能分析,取不同码长p=63,255,1023,调制位数G=3,不同信噪比下,分析算法收敛性。采样周期为Tc。 图3 不同码长下算法估计性能 由图3可知,随着码长的增加,算法达到收敛所需数据组数越大,运算量也相应的增加。相同信噪比下,码长越长,所需数据组数越大。 图4 不同信噪比下的收敛性能 由图4可以看出在较低信噪比下,本文所提算法依然具有良好的估计性能。 实验2:与文献[5]所提算法进行比较,取码长p=255,调制位数G=3,不同信噪比情况下,进行仿真分析,每种情况下进行了500蒙特卡洛仿真。 图5 不同算法性能比较 由图5可以看出,本文所提算法与文献[5]中算法相比,只需更少的数据组数即可快速收敛。且相同信噪比下,本文算法能更快达到收敛。同时反映了本文所提算法运算量较小。 5结语 本文提出了一种基于Viterbi算法的周期长码直扩信号的扩频序列估计算法。该算法首先将周期长码直扩信号等效建模为多用户短码直扩信号模型。在此模型的基础上,利用Viterbi算法实现对长码扩频序列的盲估计。仿真结果验证了该算法的有效性,该算法在较低信噪比依然有很好的估计性能,通过增加数据窗长度还可以增加估计的精度。 参 考 文 献 [1] 牟青.直接序列扩频信号的截获分析研究[D].成都:电子科技大学博士学位论文,2010:45-55. MU Qing. Analysis and Research on interception of direct sequence spread spectrum signals[D]. Chendu: University of Electronic Science and Technology,2010:45-55. [2] M. K. Tsatsanis, G. B. Giannakis. Blind estimation of direct sequence spread spectrum signals in multipath. Signal Processing[J]. IEEE Trans. Signal Processing,1997,45(5):1241-1252. [3] Z. Q. Dong, N. Y. Hu. A method for the detection of long pseudo-random code DSSS signals based on the processing of delay-multiply(Ⅱ)- the estimation of the information symbol period and the pseudo-random code sequence[C]//IEEE 11th Int. Conf. on Communication Technology Proceedings,2008:233-236. [4] S. Daneshmand, H. Aghaeinia, M. Tohidian, et al. Blind estimation of signal in periodic long-code DSSS communications[J]. IEEE Sarnoff Symposium,2009,32:1-6. [5] 白娟,张天骐,赵德芳,等.基于虚拟多用户模型的长码直扩信号伪码估计[J].电讯技术,2011,51(8):29-35. BAI Juan, ZHANG Tianqi, ZHAO Defang, et al. PN Sequence Estimation of Long-code DSSS Signal Based on Virtual Multiuser Model[J]. Telecommunication Engineering,2011,51(8):29-35. [6] 周德强,陈卫东.基于Viterbi算法的扩频码与信息序列联合估计[J].飞行器测控学报,2014,33(5):441-447 ZHOU Deqiang, CHEN Weidong. Joint Blind Estimation of Spreading Code and Information Sequence Based on Viterbi Algorithm[J]. Journal of Spacecraft TT&C Technology,2014,33(5):441-447. [7] 周德强,康一定,陈卫东.基于Fast-ICA的周期长码直扩信号盲扩频码估计[J].无线电通信技术,2013,9(6):55-59. ZHOU Deqiang, KANG Yiding, CHEN Weidong. Blind Estimation for Spread Spectrum Codes of PLC DSSS Signals Based on Fast-ICA[J]. Radio Communications Technology,2013,9(6):55-59. [8] 任啸天,徐晖,王翔,等.一种针对短码、周期长码直扩信号的扩频序列盲估计方法[J].宇航学报,2011,32(12):2596-2600. REN Xiaotian, XU Hui, WANG Xiang, et al. A Method for Blind Estimation of PN Sequence of Short-code and Periodic Long-code DSSS Signal[J]. Journal of Astronautics,2011,32(12):2596-2600. [9] Chen Yongqian, Xiao Xiaoci. PN code sequence estimation using tabu search[C]//IEEE International Symposium on Communications and Information Technology(ISCIT 2005). Beijing,2005:1315-1318. [10] Peng Yanhua, Tang Bin, Lv Ming. Fast method for spreading sequence estimation of DSSS signal based maximum likelihood function[J]. Journal of Systems Engineering and Electronics,2010,21(6):948-953. [11] 程云鹏,张凯院,徐仲.矩阵论[M].3版.西安:西北工业大学出版社,2006:109-121. CHENG Yunpeng, Zhang Kaiyuan, Xu Zhong. Theory of Matrices[M]. 3rd Edition. Xi’an: Northwestern Polytechnical University Press,2006:109-121. [12] 褚振勇,易克初,田红心.非相干解扩解调信号的范数计算方法[J].西安电子科技大学学报:自然科学版,2004,31(5):705-708. ZHU Zhenyong, YI Kechu, TIAN Hongxin. A Norm Method for Noncoherent Despreading/Demodulation Signal[J]. Journal of Xidian University(Natural Science Edition),2004,31(5):705-708. Blind Estimation of Spread Spectrum Sequence of Periodic Long-code DSSS Signal WANG Jianxiong1ZHANG Limin2MA Chao1 (1. Department of Electronic and Information Engineering, Naval Aeronautical and Astronautical University, Yantai264001)(2. Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai264001) AbstractThis paper discusses blind estimation of periodic long-code(PLC) direct sequence spread spectrum(DSSS) signal. To solve it, a new blind estimation algorithm based on Viterbi search is proposed. First, a PLC DSSS signal is modeled as equivalent to a multiuser short-code DSSS system, which simplifies the problem to the estimation of short-code DSSS. Then, the Viterbi algorithm to achieve spread spectrum sequence estimation. Finally, in order to obtain the required spreading code, all the estimated spreading code of each virtual user are sumed up. Both theoretical analysis and computer simulations show that the approach works well on the lower SNR ambient and has small computation amount. Key Wordsperiodic long code, direct sequence spread spectrum, spread spectrum sequence estimation, Viterbi algorithm, blind estimation 收稿日期:2015年12月17日,修回日期:2016年1月19日 基金项目:国家自然科学基金(编号:60972159;61102167);航空科学基金(编号:20085184003);泰山学者工程专项经费(编号:ts201511020)资助。 作者简介:王建雄,男,博士研究生,研究方向:盲信号处理。张立民,男,博士,教授,研究方向:通信信号处理。马超,男,博士研究生,研究方向:盲信号处理。 中图分类号TN911 DOI:10.3969/j.issn.1672-9722.2016.06.011