计算机模拟技术预测井筒涌水量的应用研究

刘小满　赵万里　钱自卫

(1.平顶山学院软件学院　平顶山　467000)

(2.中国平煤神马集团炼焦煤资源开发及综合利用国家重点实验室　平顶山　467000)

(3.中国平煤神马集团能源化工研究院　平顶山　467000)

(4.中国矿业大学深部岩土力学与地下工程国家重点实验室　徐州　221116)

计算机模拟技术预测井筒涌水量的应用研究

刘小满1赵万里2,3钱自卫4

(1.平顶山学院软件学院平顶山467000)

(2.中国平煤神马集团炼焦煤资源开发及综合利用国家重点实验室平顶山467000)

(3.中国平煤神马集团能源化工研究院平顶山467000)

(4.中国矿业大学深部岩土力学与地下工程国家重点实验室徐州221116)

摘要计算机模拟技术作为一种比较先进的技术手段,利用其技术优势弥补了解析法、类比法等传统预测法的不足,对井筒涌水量的预测更加符合实际。论文以平煤股份十矿三水平进风井平顶山砂岩含水层段为例,采用计算机数值模拟软件COMSOL,构建数值计算模型,对井筒的开挖过程进行数值模拟,实现了不同施工工况下,井筒涌水量的预测分析。模拟结果为建井方式的合理设计及井筒安全施工提供了理论依据。

关键词计算机; 数值模拟技术; COMSOL软件; 井筒涌水量; 含水层

Class NumberTP391.9

1引言

井筒涌水量的准确预测对于矿井井筒的建设至关重要,只有在预知井筒涌水量的情况下,才能合理选择建井方式,以顺利进行矿井建设;反之,选择了不合理的建井方式造成严重经济浪费、延误工期,甚至酿成严重工程事故。

随着计算机应用技术的发展,计算机模拟技术成为近年来一种比较先进的技术手段[1～2],其效率高,周期短,工作量简化,精度较高,能较为真实地描述研究区域的水文地质特征及边界性质,弥补了解析法、类比法等传统预测法的不足[3～7],对井筒涌水量的预测更加符合实际,具有极佳的发展潜力与应用前景。本文选用计算机模拟软件COMSOL[8～9],以平煤股份十矿三水平进风井平顶山砂岩含水层段为例,进行井筒涌水量预测,以便为工程合理设计与安全施工提供理论依据。

2含水层一次全段开挖数值分析

2.1数值计算模型

进风井地层数据依据与其相距61m已建三水平回风井实际揭露资料:进风立井净径8.0m,支护厚度0.6m,井筒开挖直径9.2m,井口标高+223.000m,井底标高-896.572m,井深1119.572m,含水层厚度97.0m,含水层顶面埋深325.6m,底面埋深为422.9m,渗透系数为0.0533m/d。十矿三水平十矿北二进风井平顶山砂岩含水层段揭露井筒涌水量数值计算模型如图1所示。模型整体为1/4圆柱体,圆柱体半径为300m,厚度为平顶山砂岩含水层段厚度97m。

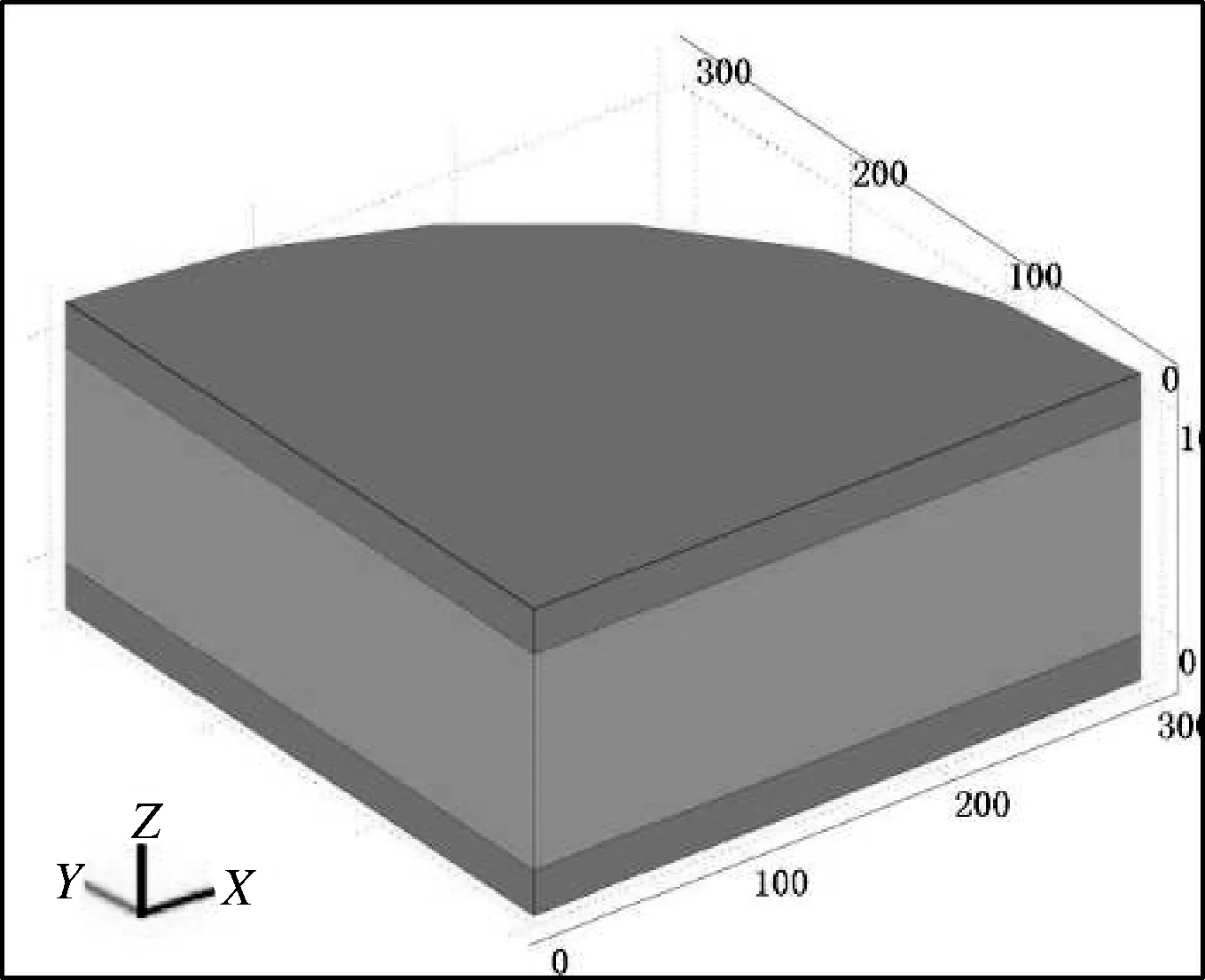
图1　井筒涌水量数值计算模型

2.2边界条件

假设井筒开挖涌水为中心对称模式,建立的井筒涌水量计算模型采用1/4单元模块,由此可减小计算的数据量,并且使计算结果更易呈现。纵向上地层的外边界施加自然水头边界条件,井筒的水头边界条件为:402.9-z;地层的1/4纵切面为对称无通量边界;井筒内壁面在相对隔水层段为对称无通量边界,在含水层段为自由出流边界(水压为0)。

2.3计算结果

图2～图4为井筒在平顶山砂岩含水层段一次全段开挖工况下,开挖后井筒围岩的压力水头及渗流速度场分布计算结果。

1) 压力水头变化

图2所示为井筒开挖前后围岩压力水头分布云图。对比分析可知,井筒未开挖含水层压力水头随着地层埋深呈线性增大。井筒开挖后其压力水头发生明显的变化,整体表现为井筒附近压力水头出现了显著降低现象,距离井筒越远压力水头降低的幅度越小。

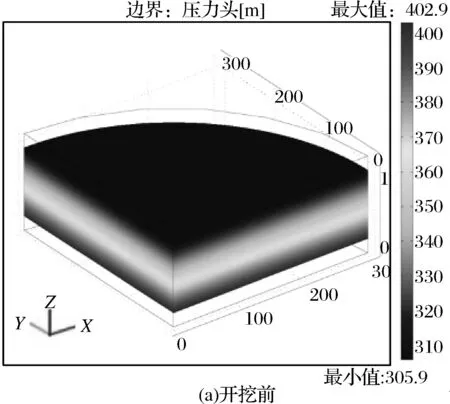
图2　井筒开挖前后围岩水压分布云图

图3为井筒596m井段开挖后平顶山砂岩含水层底面压力水头分布云图及径向分布曲线图。分析可知,井筒开挖后,井筒围岩的压力水头呈现由外部围岩到井筒逐渐减小的特征,减小的速率呈现快-慢-快的过程。在距离井筒300m～50m左右减小的速率相对较缓,距离井筒0m～50m范围减小的速率逐渐加快,在井壁位置压力水头减小到0。

2) 速度场特征

图4所示为井筒开挖后平顶山砂岩含水层底面渗流速度场分布云图及径向分布曲线图。井筒开挖后,井筒围岩即产生渗流现象,随着与井筒中心距离的变小,渗流速度呈现平稳-增大-激增的过程。在距离井筒300m～150m范围渗流速率相对稳定在一个低值,距离井筒150m～30m范围渗流速率逐渐加快,特别是在30m～0m段内渗流速率急剧增加。

图3　井深596m处平面上井筒开挖后围岩压力水头分布图

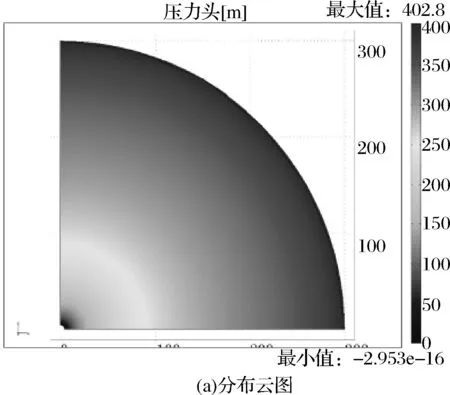
图4　井深596m处平面上井筒开挖后围岩渗流速度场分布图

3) 涌水量计算结果

数值计算软件中涌水量的计算采用积分法,即对井壁在含水层段的通量进行积分,获得涌水量数据,计算所得进风井平顶山砂岩含水层段一次挖全高的情况下的井筒涌水量为112.59m3/h,此预测计算结果与传统的解析法相近。

3含水层分段掘砌数值分析

实际的井筒施工过程中,不可能出现深厚的含水层一次开挖完成后再筑壁的情况,而是边掘进边支护,工序交叉一般在10 m左右,即井筒连续开挖10 m左右,然后进行浇筑井壁浇筑完成后继续开挖下一段,如此循环。以进风井在平顶山砂岩含水层段分段掘进为例,研究井筒在含水层中分段掘砌压力水头变化特征、渗流速率变化特征及涌水量。

3.1数值计算模型

构建数值计算模型如图5所示,模型整体为1/4圆柱体,圆柱体半径为300m,厚度为平顶山砂岩含水层(含水层)段厚度97m,井筒的直径为8.0m,支护厚度0.6m,井筒开挖直径9.2m。

图5　井筒分段掘进数值计算模型

3.2边界条件

纵向上模型的外边界施加自然水头边界条件,副井的水头边界条件分别为:251-z;地层的1/4纵切面为对称无通量边界;井筒壁面在相对隔水层段为对称无通量边界,在含水层段井壁支护前为自由出流边界(水压为0),支护后设定井壁不渗水。

3.3分段开挖控制

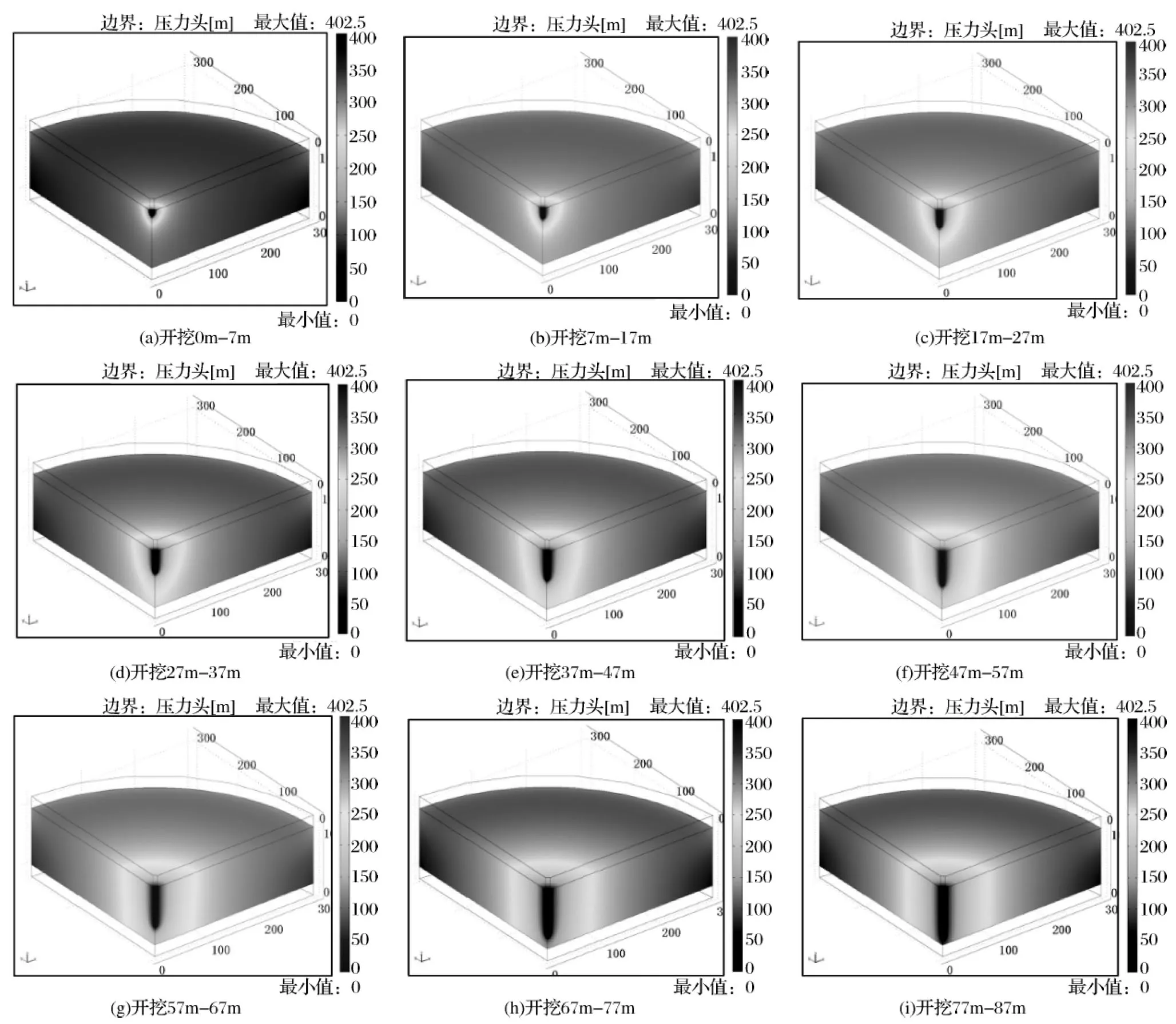
井筒开挖设定为分段开挖,分段开挖的井径为9.2m,分段深度为10m/段,即0m～10m﹑10m～20m﹑20m～30m﹑30m～40m﹑40m～49m。开挖又分为开挖后支护及不支护两种情况。

3.4计算结果

1) 压力水头变化特征

图6为分段开挖不支护工况的水压水头变化云图。

多层空间的状态特征矩阵描述为

根据计算结果,如图6、图7所示与一次性全段开挖相比,井筒分段开挖过程围岩的水压发生明显变化,主要表现为距离井壁越近水压降低幅度越大的特征;不同开挖深度条件下,围岩水压降低的幅度不同,降低的幅度随着井筒开挖深度的增加而增大。

图7　分段开挖不支护工况含水层底面压力水头变化曲线

井筒开挖支护后,如图8、9所示,井筒围岩的压力水头变化特点与不支护工况相近,也表现为距离井壁越近压力水头降低幅度越大的特征,但与不支护相比,井壁支护后的壁后压力水头有明显的回升现象;不同开挖深度条件下,围岩压力水头降低的幅度大致一致,含水层底面压力水头降低的幅度随着井筒开挖深度的增加而呈现逐步增大的趋势。

图10为支护及不支护两种工况井筒完成开挖后含水层底面的压力水头曲线。分析可知,井筒开挖,围岩的压力水头均出现近似漏斗状的水力坡降。对比而言,不支护工况下压力水头坡降波及的范围要明显大于支护工况条件。

2) 涌水量

数值计算软件中涌水量的计算采用积分法,即通过对井壁在含水层段的通量进行积分获得涌水量数据。井筒分段开挖涌水量计算结果如图11所示。

分析结果反映出,在采用分段开挖的情况下,如开挖后不支护,则井筒的涌水量随着开挖深度的增加而增加,但增加的幅度逐渐放缓;如分段开挖后及时支护,则井筒的涌水量明显小于不支护工况下的涌水量,且表现有随着开挖深度的增加,涌水量呈现先增加后降低的变化过程。

图8分段开挖支护(掘砌)工况的压力水头变化云图

图9　分段开挖支护(掘砌)工况下含水层底面压力水头变化曲线

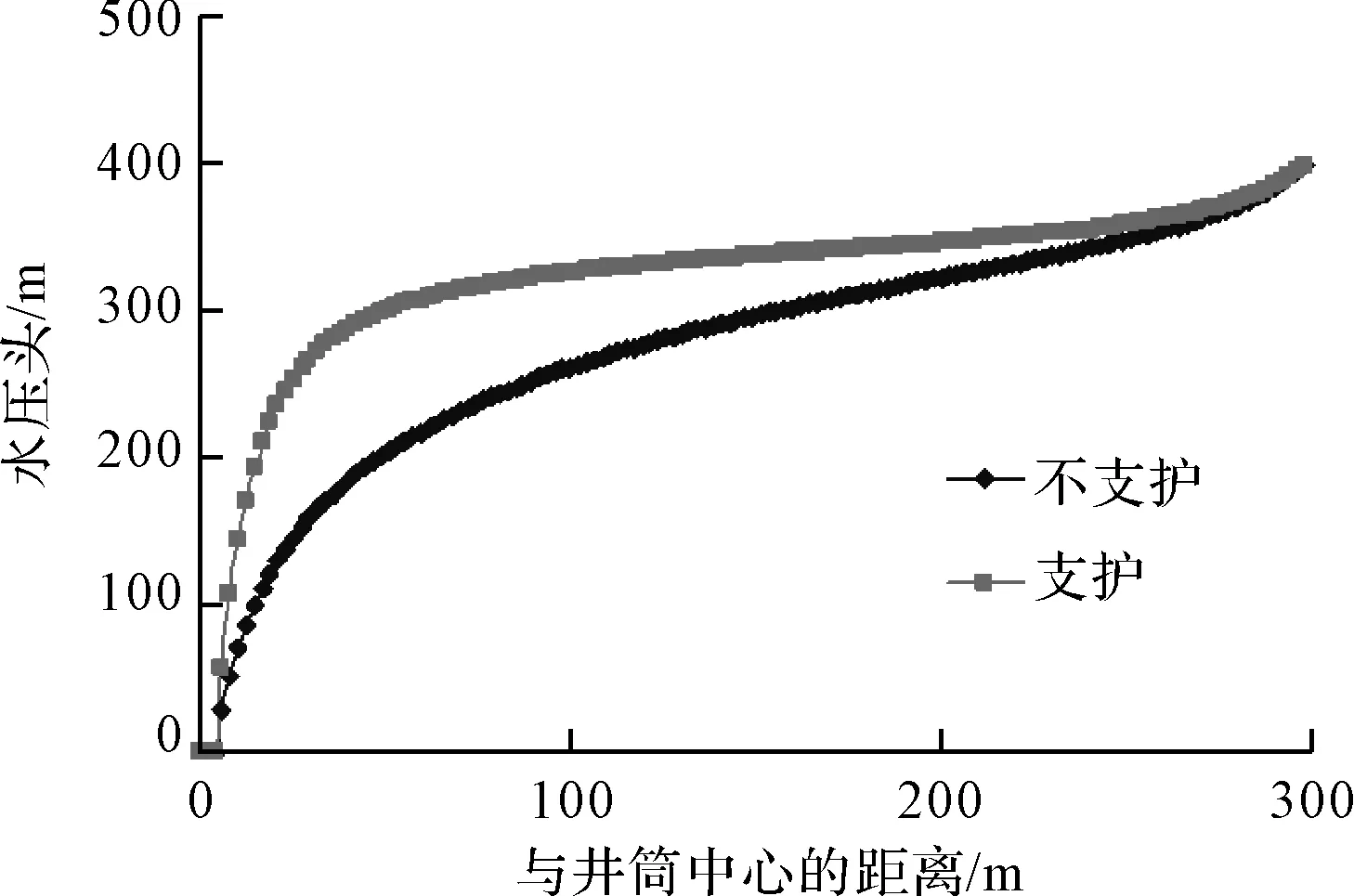
图10　最后一段开挖含水层底面的压力水头变化曲线

图11　井筒分段开挖涌水量与开挖深度关联曲线

4结语

1) 利用计算机数字模拟软件对平顶山砂岩含水层一次全段开挖进行数值析,结果发现:进风井平顶山砂岩含水层段一次挖全高的情况下的井筒涌水量为112.59m3/h,此预测计算结果与传统法相近。

2) 实际的井筒施工过程中,采用的是边掘进边支护,再次构建模型模拟发现,井筒的涌水量明显小于不支护工况下的涌水量,且表现有随着开挖深度的增加,涌水量呈现先增加后降低的变化过程。

3) 采用COMSOL计算机模拟技术,预测建井过程中的井筒涌水量,模拟结果对平煤股份十矿三水平进风井建井方式的合理设计及安全施工提供了理论依据。

参 考 文 献

[1] 王国瑞,冯书顺,翟延亮.等.基于Visual Modflow的矿井涌水量数值模拟精细预测研究[J].煤炭技术,2015,34(8):191-194.

WANG Guorui, FENG Shushun, ZHAI Yanliang, et al. Fine Prediction of Numerical Simulation for Mine Water Inflow Based on Visual Modflow[J]. Coal Technology,2015,34(8):191-194.

[2] 王亮.基于Visual MODFLOW预测矿井涌水量[D].青岛:山东科技大学,2012.

WANG Liang. Forecasting Inflow of Mine by Visual Modflow[D]. Qingdao: Shandong University of Science and Technology,2012.

[3] 李磊.数值模拟在矿井涌水量预测中的应用[J].煤矿开采,2014,19(3):126-128.

LI Lei. Application of Numerical Simulation in Water Inflow Prediction of mine[J]. Coal Mining Technology,2014,19(3):126-128.

[4] 马青山,骆祖江.解析法与数值法在矿井涌水量预测中比较[J].矿业安全与环保,2015,42(4):63-66.

MA Qingshan, LUO Zujiang. Comparison of Analytical Method and Numerical Method in Mine Water Inflow Prediction[J]. Mining Safety & Environmental Protection,2015,42(4):63-66.

[5] 马秀媛,李逸凡,张立.等.数值方法在矿井涌水量预测中的应用[J].山东大学学报(工学版),2011,41(5):86-91.

MA Xiuyuan, LI Yifan, ZHANG Li, et al. Numerical Methods in Predicting Mine Discharge[J]. Journal of Shandong University(Engineering Science),2011,41(5):86-91.

[6] 薛禹群.水文地质学的数值法[M].北京:煤炭工业出版社,1986.XUE Yuqun. Numerical Methods of Hydrogeology[M]. Beijing: China Coal industry Publishing House,1986.

[7] 魏军.矿井涌水量的数值模拟研究[D].阜新:辽宁工程技术大学,2006.

WEI Jun. Numerical Simulation of Mine Discharge[D]. Fuxin: Liaoning Technical University,2006.

[8] 连会青,夏向学,徐斌.等.矿井涌水量预测方法及适用性评价[J].华北科技学院学报,2014,11(2):22-27

LIAN Huiqing, XIA Xiangxue, XU Bin, et al. Evaluation and Applicability Study on Prediction Methods of Water Inflow in Mines[J]. Journal of North China Institute of Science and Technology,2014,11(2):22-27.

[9] 张林栋,刘传皓.沸石交换柱内流体流动特性模拟[J].河北工业大学学报,2014,43(5):55-59.

ZHANG Lindong, LIU Zhuanhao. Simulation of the Fluid Flow Characteristics in the Zeolite Exchange Column[J]. Journal of Hebei University of Technology,2014,43(5):55-59.

[10] 张玉宝,李强.基于COMSOL Multiphysics的MEMS建模及应用[M].北京:冶金工业出版社,2007.

ZHANG Yubao, LI Qiang. MEMS Modeling and Application by COMSOL Multiphysics[M]. Beijing: Metallurgical Industry Press,2007.

Application of Computer Simulation Technology in Prediction of Wellbore Inflow

LIU Xiaoman1ZHAO Wanli2,3QIAN Ziwei4

(1. College of Software, Pingdingshan University, Pingdingshan467000)

(2. State Key Laboratory of Coking Coal Exploitationand Comprehensive Utilization,China Pingmei Shenma Group, Pingdingshan467000)

(3. Institute of Energy and Chemical Industry, China Pingmei Shenma Group, Pingdingshan467000)

(4. National Key Lab of Geomechanics and Underground Enginnering,China University of Mining and Technology, Xuzhou221116)

AbstractAs a more advanced technology, computer simulation technology used its technological advantage to make up for the lack of analytical method, analogy method and other traditional prediction methods, and predict more realistically of water inflow into the wellbore. In this paper, taking Pingdingshan sandstone aquifers section of air shaft into three levels of Pingdingshan shares tenth coal mine as an example, The computer simulation software COMSOL was applied for the shortcomings of the traditional method of the shaft inflow forecasting with constructing of mathematical models to analyze the excavation process of the wellbore, achieving the wellbore inflow forecasting analysis on the different construction conditions. Simulation results that provide a theoretical basis for the reasonable design of mine construction methods and the safe construction of wellbore.

Key Wordscomputer, numerical simulation technology, COMSOL software, wellbore inflow, aquifers

收稿日期:2015年12月8日,修回日期:2016年1月19日

基金项目:国家重点基础研究发展计划(973)项目(编号:2013CB036003)资助。

作者简介:刘小满,女,硕士,助教,研究方向:计算机应用、软件开发。赵万里,男,硕士,工程师,研究方向:煤矿技术。钱自卫,男,博士研究生,研究方向:煤矿工程地质及灾害治理。

中图分类号TP391.9

DOI:10.3969/j.issn.1672-9722.2016.06.003