基于改进A*算法的无人机航迹规划

张帅, 李学仁, 张鹏, 李博

(1.空军工程大学 航空航天工程学院, 陕西 西安 710038;2.航空电子系统综合技术重点实验室, 上海 200233)

基于改进A*算法的无人机航迹规划

张帅1,2, 李学仁1, 张鹏1, 李博1

(1.空军工程大学 航空航天工程学院, 陕西 西安 710038;2.航空电子系统综合技术重点实验室, 上海 200233)

摘要:借鉴A*算法思想,提出了一种改进A*算法的无人机航迹规划方法。针对在传统A*算法中将规划区域栅格化、只能在特定方向按照特定步长扩展节点的不足,采用圆形节点扩展方法,可以实现变方向和变步长扩展节点。通过仿真进行了验证,结果表明改进的航迹规划方法可以绕过威胁,安全到达目标点。

关键词:无人机; 航迹规划; 节点扩展

0引言

目前,国内外对无人机的航迹规划已进行了大量的研究,关于航迹规划的方法也有很多,特别是大量的智能算法,如:蚁群算法、神经网络法、粒子群算法、遗传算法、模拟退火算法等。文献[1]运用粒子群算法和遗传算法对无人机进行了航迹规划,对比了这两种方法,遗传算法存在费时、遗传因子不好选择的缺点,在接近最优解时,收敛速度会很慢;而粒子群算法在复杂问题上有早熟收敛和收敛性能差的缺点。文献[2]将蚁群算法运用到无人机航路规划中,其缺点是容易陷入局部最优的陷阱，并且收敛速度较慢。文献[3]采用模拟退火算法进行无人机航迹规划,该算法对初始解有较强的依赖性,可能陷于局部最小,虽然理论上可以跳出来,但需要经过很长的时间。

本文在借鉴了A*算法思想的基础上,提出了一种新的、易实现的改进型A*无人机航迹规划方法。传统的A*算法将规划区域栅格化,节点扩展只限于栅格线的交叉点,扩展方向和步长都受到了限制。本文采用圆形节点扩展法,从起始位置出发,先确定最佳扩展方向,然后根据设定的步长,得到下一扩展点,再以下一扩展点为初始位置,继续搜寻最佳扩展方向,按照步长得到下一扩展点,如此循环,直至到达目标点。最后,通过仿真验证了算法的可行性。

1问题描述

无人机航迹规划是根据任务需要,在给定的规划空间里,在满足地形限制、敌方雷达、防空火力威胁、气象分布、自身机动特性等一系列约束条件下,找到一条从起始点到目标点的最满意或最优的路径,使得所花代价最小,安全系数最高,并保证任务能圆满完成[4]。航迹规划涉及的学科和知识较广,是一项比较复杂的工程。

无人机实际飞行过程包括起飞、爬升、巡航、下降、着陆等阶段。本文主要针对无人机在巡航阶段的航迹规划进行研究,假设无人机在飞行过程中高度和速度保持不变,则航迹规划就变为一个在二维平面的规划问题。

2威胁模型

在无人机飞行过程中,会遇到各种各样的威胁,主要包括:(1)地形威胁:防止飞行过程中与山峰碰撞或低于安全高度而坠地;(2)雷达和火力威胁:防止被探测到而击落;(3)气象威胁:防止误入气象条件复杂的空间;(4)敌方设置的禁飞区等。无人机需要及时地规避各种威胁,所以在进行航迹规划时,需要对威胁信息有充分的考虑。而在这些威胁中,最主要的来源是地形威胁和敌方雷达的探测威胁,因此,本文重点考虑这两种威胁。

2.1地形威胁

很多情况下,无人机在执行任务时,由于山峰等对雷达形成探测盲区,需要借助地形的掩护,实行低空突防[5]。但进行低空突防时,由于飞行高度比较低,容易发生碰撞,致使无人机坠毁。所以,在飞行过程中,山峰地形是一个很大的威胁。本文采用如下函数建立山峰威胁概率模型:

(1)

式中:(xpi,ypi)为第i个山峰中心点在平面上的位置坐标;λ为一个参数,可以通过λ来调节山峰在二维规划平面上威胁作用距离;(x,y)为二维规划平面上的一点;fp(x,y)为关于点(x,y)到山峰中心点坐标(xpi,ypi)的距离函数,表示发生碰撞的概率。假设某山峰中心点坐标是(15,15) km,λ=0.1。通过仿真,模拟得到的山峰威胁如图1所示。

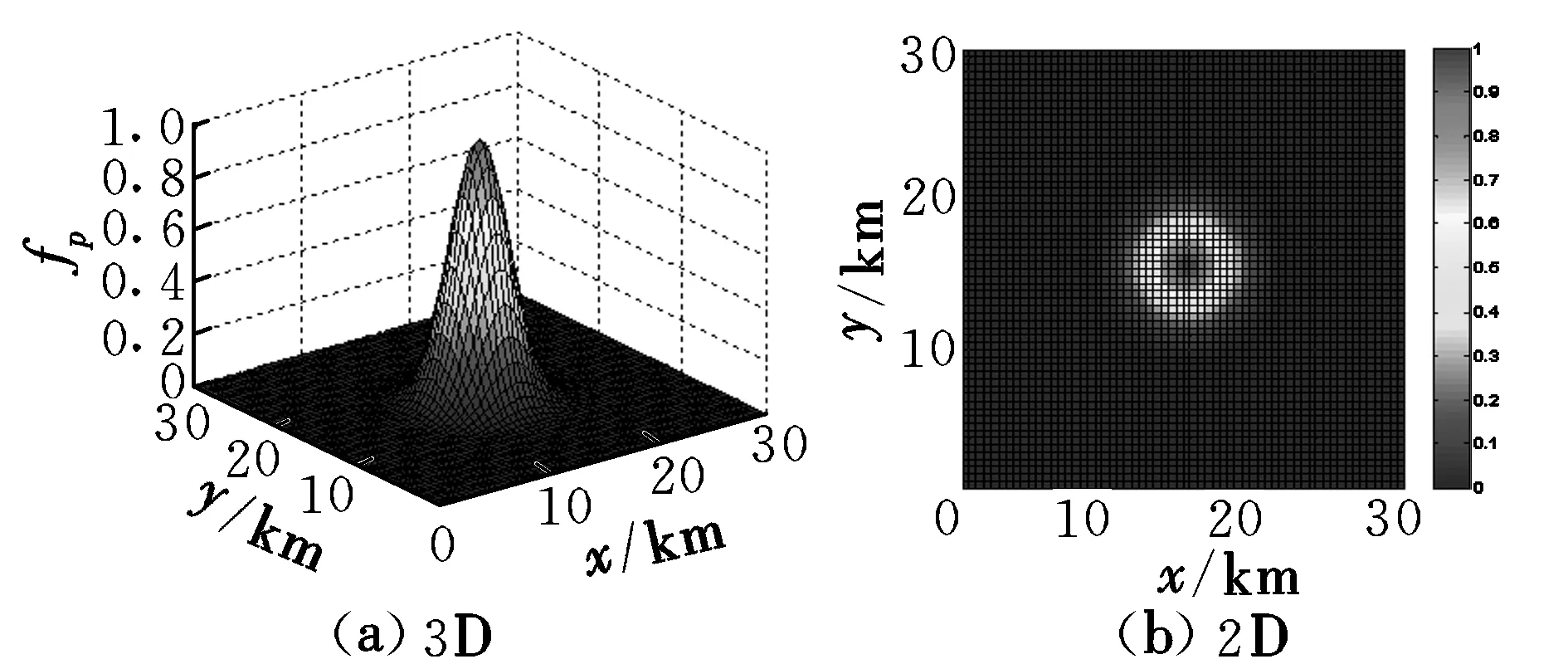
图1　山峰威胁模拟Fig.1　Simulation of mountain peak

从图1中可以看出,距离山峰中心点越近,受威胁概率越大。因为距离越近时,留给无人机通过改变航迹绕过山峰的时间将越短,无人机采取机动规避的难度将加大,发生碰撞的可能性增大。

2.2雷达威胁

随着导弹技术的快速发展,防空导弹变得越来越先进,突破敌方防空区的难度增大,风险系数增高。现代战争中,发现即意味着摧毁,当无人机在执行任务时,如果被敌方的雷达探测到并跟踪锁定,摧毁的概率几乎为1,所以在此只考虑被雷达探测到的威胁而不考虑防空火力的威胁,雷达威胁是航迹规划中一个绝对不能忽视的因素[6]。雷达威胁与山峰威胁有相似之处,比如距离越近,被探测概率越大,对无人机威胁越大,在此,采用山峰威胁模型来近似模拟雷达威胁。采用这种模型可以简化航迹规划过程中威胁的表达,以便占用较少的时间和系统资源。雷达威胁概率模型为:

(2)

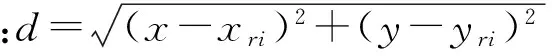
3约束条件

为保证规划的航迹是可飞的,符合无人机的气动特性和机动性能,需要考虑其自身的性能约束条件。无人机在巡航飞行过程中主要受最大航程、最小步长、最小转弯半径等条件约束[7]。

(1)最大航程

最大航程表示无人机总航迹不能超过一个特定的值,因为无人机所携带的燃料是有限的,飞行时间有限。从起始点到目标点的所有可行航迹都受最大航程的约束,在航迹规划的寻优过程中,航迹是由很多个小段的航迹连接而成,假设第i段航迹长度为li,最大航程为Lmax,则必须满足:

(3)

(2)最小步长

最小步长lmin是指无人机由于惯性作用,在改变飞行姿态前需要直飞的最短距离,即在单位时间内,以最小速度飞行的距离。必须满足以下关系:

(4)

(3)最小转弯半径

最小转弯半径指无人机改变航向,在水平面内做圆周运动时,圆周的最小半径。无人机由于受性能影响而不能转弯过急,最小转弯半径受最大转弯角φ限制,转弯角越大,则转弯半径越小。转弯半径如图2所示。

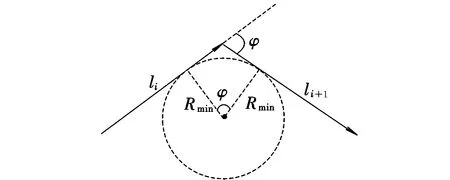
图2　最小转弯半径Fig.2　Minimum turning radius

无人机做圆周运动时,向心力是由无人机倾斜时的侧向力提供,根据文献[8-9],最小转弯半径满足如下关系式:

(5)

式中:v为无人机飞行速度;γmax为最大倾斜角。通过控制倾斜角,就可以使无人机满足最小转弯半径的约束。

4算法思想

4.1算法描述

本文在A*算法的基础上,提出了一种新的改进方法。其基本思想是:

(1)初始化参数,确定规划区域,并对规划区域的地形和雷达威胁进行建模,得到威胁概率模型;

(2)从当前位置出发,根据圆形节点扩展方法确定最佳扩展方向,选择步长,得到最佳待扩展节点,作为下一个飞行位置,然后无人机从当前节点位置飞到规划的下一位置;

(3)判断此时的待扩展节点是否为目标点。如果不是目标点,则将此时的扩展节点作为当前节点,重复步骤(2)和(3);如果是目标点,则规划结束,无人机到达目的地。

4.2节点扩展

传统的A*算法采用栅格化的方法,将规划区域划分成无数小栅格,节点扩展主要限定在栅格线的交叉点上,如图3所示。

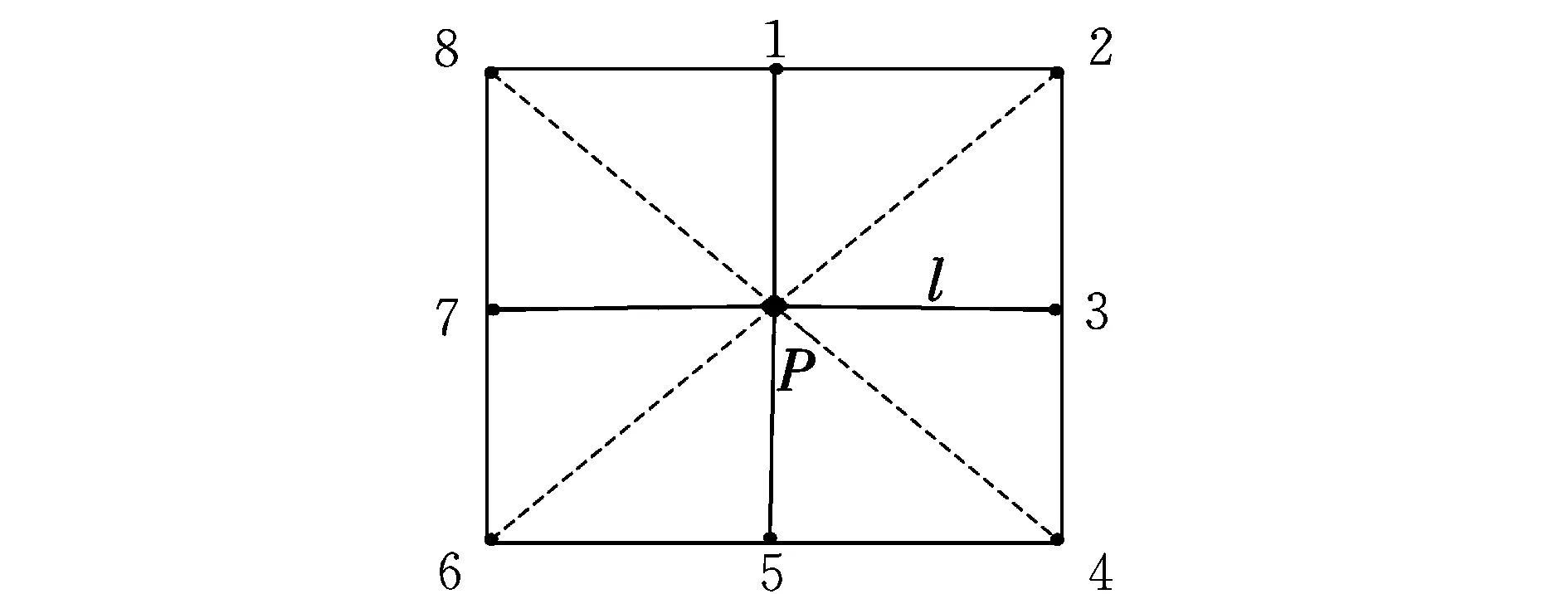
图3　栅格法节点扩展Fig.3　Grid node expansion

针对这种局限性,本文提出了一种可变方向和步长的节点扩展法,并将之命名为“圆形节点扩展法”。即以当前节点P为圆心,无人机的雷达探测距离r为半径,得到一个圆,然后在圆弧上等距离地选取N个点,限定待扩展方向为在当前节点与这N个点的连线上。这样从当前节点P出发,总共有N个待扩展的方向,然后,通过计算这N个点的代价值,选取其中代价值最小的那个点Pi(i=1，…，N),则PPi连线所在方向就是最佳扩展方向。通常由于无人机受体积和结构限制,所携带的雷达探测距离相对于地面敌方雷达的探测距离要小很多,所以如果Pi落在敌方雷达的探测范围内时,其威胁代价值较高,当Pi代价值最小时,则PPi连线必定不在雷达探测区域内,其所在方向必为最佳扩展方向,PPi连线上所取的节点要优于其他方向的节点。

确定了扩展方向后,考虑到无人机的实际飞行速度和雷达探测距离,步长取0.1r～r之间,沿最佳扩展方向取设定步长,就可以得到下一个待扩展节点。以N=16为例,如图4所示,假设第三个点P3代价值最小,则PP3为最佳扩展方向,再以0.2r为步长就得到下一个最佳扩展节点Pnext。

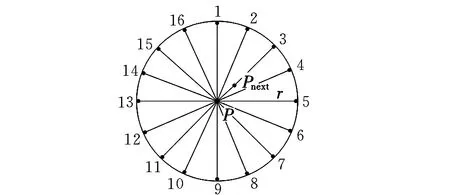
图4　圆形节点扩展Fig.4　Circular node expansion

采用这种节点扩展方法,可以保证无人机搜索到的节点尽可能接近最优路径。通过改变N的值,可以在多个方向上搜索,而不是像栅格化的方法只能在特定方向搜索。 圆弧上取的点越多,搜索的方向则越多,更易找到最优航路。但存在一个矛盾,取的点越多时,计算量增大,航迹规划的速度降低。所以,需要调节步长,搜索步长越大时,总路径的节点将越少,规划量减少,有效降低规划时间。但搜索步长过大时,又会降低航迹寻优能力,增加威胁性,所以,需要综合考虑待扩展节点的数量和搜索步长的关系,使航迹尽可能接近最优。

4.3节点代价

在4.1节中已经提到,要确定最佳扩展方向,需要计算圆弧上各点的代价值。规划的无人机航迹应使无人机在比较安全的区域飞行,保证其安全系数较高,受威胁较小,并且考虑到燃油消耗,应使航程尽可能短,所以,定义圆弧上节点Pi(i=1,2,…)的代价函数为:

(6)

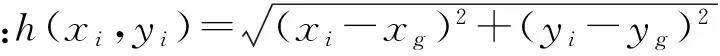
5仿真分析

5.1规划区域

设定规划区域为30 km×30 km,起始位置为(0,0) km,目标位置为(30,30) km。假设无人机的雷达探测半径r=1 km,雷达和山峰威胁的参数如表1所示。在Pentium 4(2.93 GHz),1.21 GB内存的PC机进行仿真实验,运行环境为Windows XP,通过MATLAB仿真得到的规划区域如图5所示。

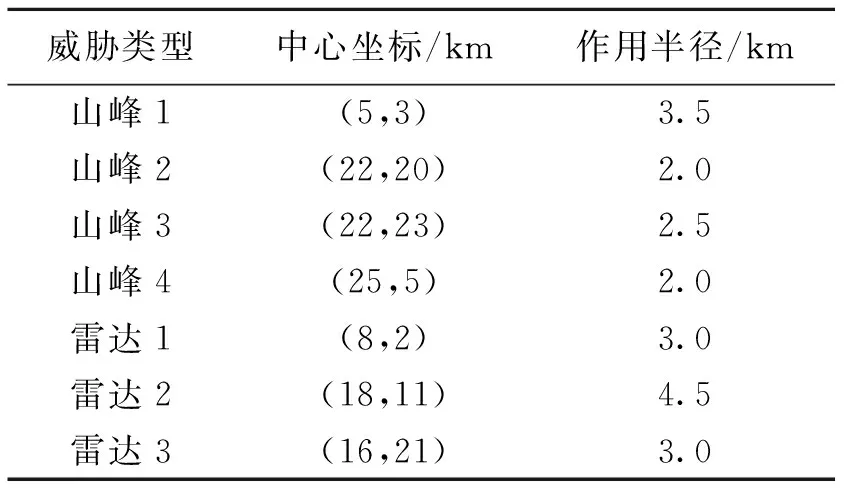
表1　威胁参数

图5　规划区域二维图Fig.5　2D planning area

5.2步长对航迹的影响

为研究步长对航迹规划的影响,分别取不同的步长进行仿真。设定权系数w1=1,w2=1×10-3,N=16,步长分别取0.1r,0.4r,0.7r和1.0r,得到在不同步长下无人机的规划航迹如图6所示。规划时间、规划步数、航程代价对比结果如表2所示。

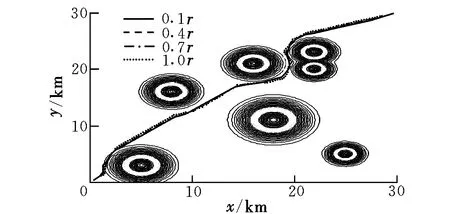
图6　不同步长下的航迹Fig.6　Flight path with different steps

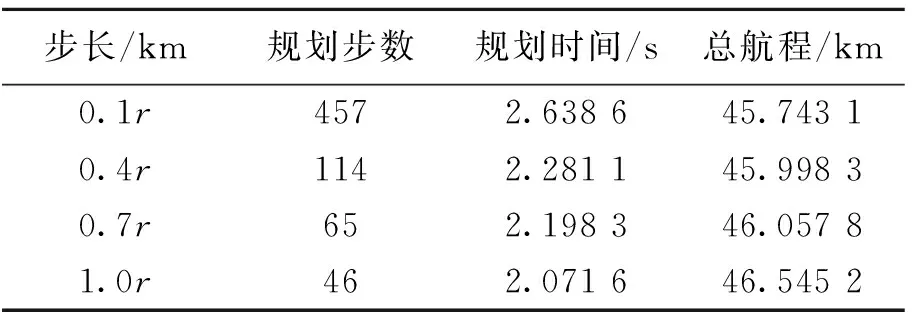
步长/km规划步数规划时间/s总航程/km0.1r4572.638645.74310.4r1142.281145.99830.7r652.198346.05781.0r462.071646.5452

由图6可知,不同步长下规划的无人机航迹都能绕过威胁区域,安全到达目标点,并且不同步长下的航迹几乎重合。可见,步长的选择对无人机路径的影响并不大,分析其原因主要是因为在节点扩展时,最佳扩展方向已经确定,并且所取的步长在雷达有效探测范围之内,都是比较安全的。

由表2可知,步长越大,从起点到目标点总共需要规划的步数则越少,规划时间越短,但总的航程变大,代价更高。因为步长越短,规划越精细,更接近于最优航迹。可见,采用小步长进行规划时,航迹更优,但实时性有所降低;而采用大步长进行规划时,实时性更好,但航程代价更高。

5.3方向对航迹的影响

为研究取不同N值时,即在不同方向搜寻扩展节点对航迹规划的影响,分别取N=8,12,16,20。其中,N=8时,与栅格法的节点扩展方向相同。统一取步长为0.4r,w1=1,w2=1×10-3,得到不同方向节点扩展时无人机的规划航迹如图7所示。

由图7可知,取不同的N值时,规划的航迹都能绕过威胁区域,安全到达目标点。但N=8时,即与传统A*算法节点扩展方向一致时,航迹是由很多段折线组成,不够平滑,存在个别航向角变化较大的拐点,并且在末段时,航迹呈锯齿状,这样的航迹不符合无人机实际飞行的要求。

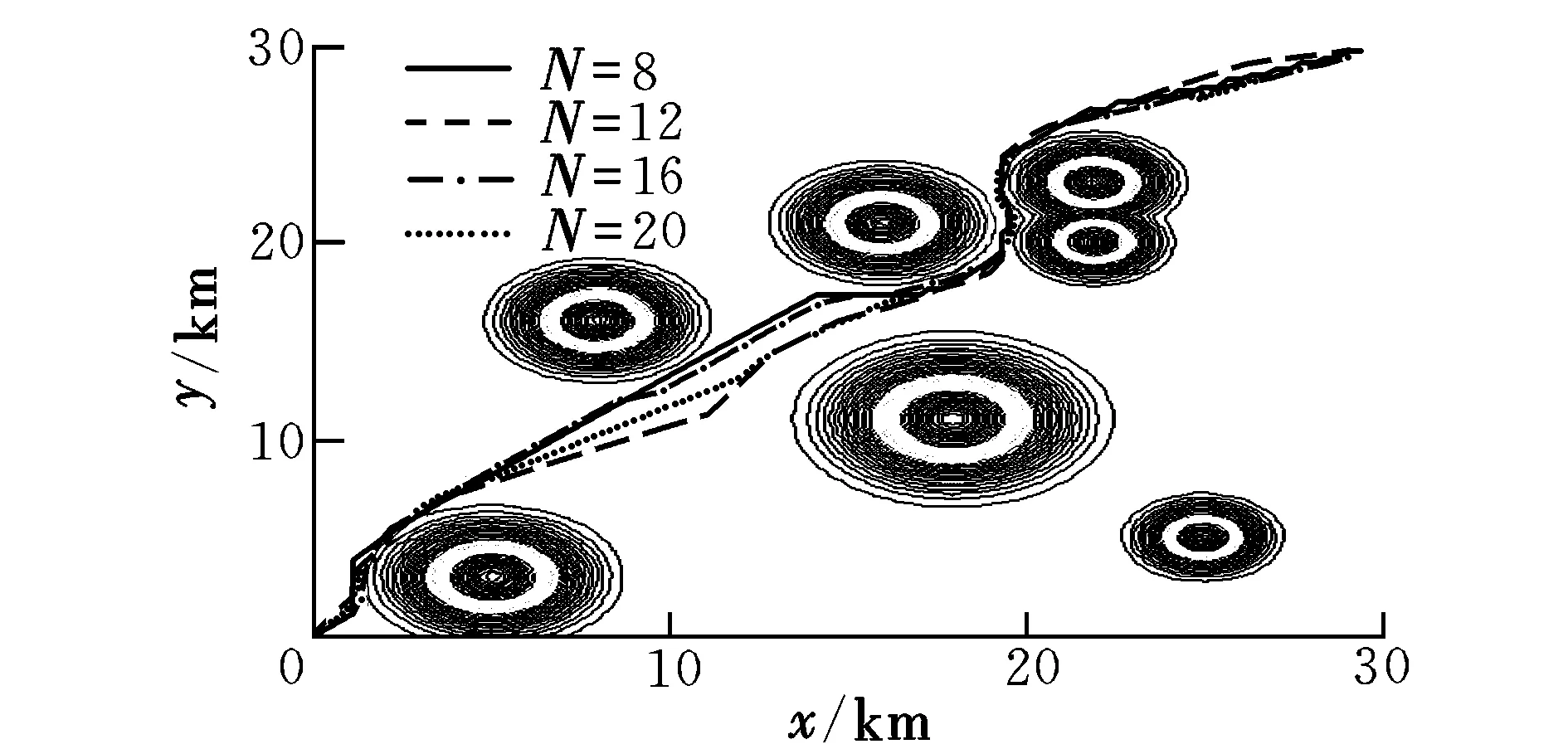
图7　不同方向下的航迹Fig.7　Planning path in different directions

规划时间、规划步数、航程代价对比结果如表3所示。由表中可以看出,N越大,总规划步数越少,总航程越短,总代价越小,但规划时间会越长。说明随着N的增大,规划出来的航迹会越来越精细,越来越接近最优值,但相应的处理速度会降低。并且,虽然航迹代价会随着N增大而变小,但变化并不是很大,说明取不同的N时,都可以有效规避威胁,其主要受影响的是航程。通过结果的对比可以得出结论,当N取16或20时,可以获得较优的航迹。

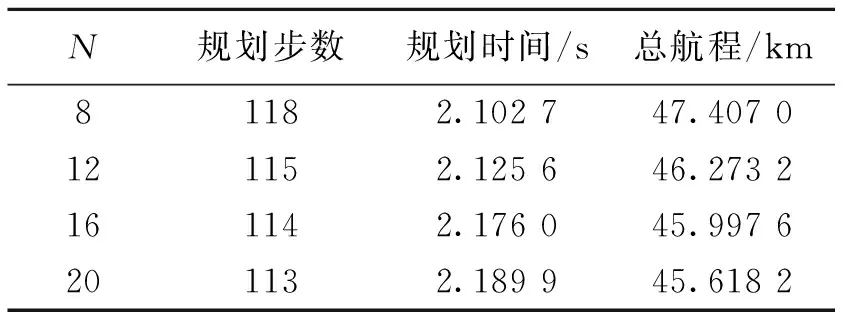
表3　不同扩展方向结果

6结束语

本文针对无人机巡航阶段,采用新的方法进行了航迹规划，提出了一种可变方向和变步长的节点扩展方法,突破了栅格化扩展节点特定方向、特定步长的约束。并通过取不同方向和步长扩展节点进行了仿真验证,对所得到的不同航迹进行了对比,结果表明所采用的航迹规划方法是可行的。

参考文献：

[1]Vincent R,Mohammed T,Gilles L.Comparison of parellel genetic algorithm and particle swarm optimization for real-time UAV path planning[J].IEEE Transactions on Industrial Informatics,2013,9(1):132-141.

[2]白俊强,柳长安.基于蚁群算法的无人机航路规划[J].飞行力学,2005,23(2):35-38.

[3]范林玉.航迹规划遗传模拟退火算法研究[D].重庆:重庆大学,2010.

[4]胡中华.基于智能优化算法的无人机航迹规划若干关键技术研究[D].南京:南京航空航天大学,2011.

[5]占伟伟,王伟,陈能成,等.一种利用改进A*算法的无人机航迹规划[J].武汉大学学报(信息科学版),2015,40(3):315-320.

[6]Karimi J,Pourtakdoust S H.A real-time algorithm for variable-objective motion planning over terrain and threats[J].Journal of Aerospace Engineering,2015,229(6):1043-1056.

[7]郑昌文,严平,丁明跃,等.飞行器航迹规划研究现状与趋势[J].宇航学报,2007,28(6):1442-1446.

[8]张洛兵,徐流沙,吴梅.基于改进人工蜂群算法的无人机实时航迹规划[J].飞行力学,2015,33(1):38-42.

[9]常波,王瑞.基于几何法的无人机航迹规划[J]. 计算机系统应用,2015,24(1):109-113.

(编辑：方春玲)

UAV path planning based on improved A*algorithm

ZHANG Shuai1,2, LI Xue-ren1, ZHANG Peng1, LI Bo1

(1.Aeronautics and Astronautics Engineering College, Air Force Engineering University,Xi’an 710038, China;2.Key Laboratory of Science and Technology on Avionics Integration Technologies,Shanghai 200233,China)

Abstract:An improved UAV path planning method was put forward considering A*algorithm. Since gridding on planning area in traditional A* algorithm could only expand nodes in a specific direction with given step, this paper adopted circular nodes expanding method, which could realize expand nodes in alterable direction and step. This method was verified by a large number of simulations. The result shows that the improved path planning method can bypass the threat and reach the target safely.

Key words:UAV; path planning; nodes expansion

收稿日期:2015-06-23;

修订日期:2015-12-08; 网络出版时间:2016-01-10 14:09

基金项目:航空科学基金资助(20145596024)； 陕西省基础研究项目(2014JQ8331)

作者简介:张帅(1992-)，男，湖南湘潭人，硕士研究生，研究方向为无人机航迹规划。

中图分类号：V279

文献标识码：A

文章编号：1002-0853(2016)03-0039-05