基于谐波观测器的Conergy NPC单相逆变器中点平衡策略

易灵芝，黄　鹤，李卫平，陈才学，陈人楷

（1.智能计算与信息处理教育部重点实验室（湘潭大学），湘潭411105；2.湖南省“风电装备与电能变换”2011协同创新中心，湘潭411101；3.惠州学院电子科学系，广州516007）

DOI：10.13234/j.issn.2095-2805．2016．1．43中图分类号：TM 46文献标志码：A

基于谐波观测器的Conergy NPC单相逆变器中点平衡策略

易灵芝1，2，黄鹤1，李卫平3，陈才学1，2，陈人楷1

（1.智能计算与信息处理教育部重点实验室（湘潭大学），湘潭411105；2.湖南省“风电装备与电能变换”2011协同创新中心，湘潭411101；3.惠州学院电子科学系，广州516007）

提出了一种对周期非正弦信号中各谐波含量实时估计的谐波观测器算法，并将其应用于中点平衡策略。在分析单相全桥Conergy NPC逆变器的开关模型与单相SVPWM调制策略基础上，研究一种基于动态控制参数的中点平衡策略；基于状态观测器原理，设计了滤波电容电压的谐波观测器，实时估计出滤波电容电压中各次谐波分量信息和分量正交信息，利用这些估计信息实现中点平衡策略。仿真和实验都验证了基于谐波观测器的中点电位平衡策略可行性与有效性。

Conergy NPC；动态控制参数；中点平衡策略；谐波观测器

Project Supported by National Natural Science Foundation of China（61572416）；Hunan Provincial Education Department Platform Project（14K095）；Key Discipline of Hunan Province “Information and Communication Engineering”in“12th Five Year Plan”

引言

三电平逆变器NPC（neutral point clamped）具有输出电压谐波含量低、EMI小、开关损耗小、滤波电感小等优点［1］。由于传统二极管型NPC使用钳位二极管，损耗与成本增加；运行时单相桥臂内、外开关管损耗程度不一，器件发热不均［2］，难于实现集成化小型化［3］，不适合分布式能源的低电压、小功率、高效率和低成本场合。为此文献［4］提出一种每相桥臂仅由4个IGBT组成的Conergy NPC拓扑。每相桥臂比二极管型NPC减少2个钳位二极管，运行时桥臂内损耗比较均衡。随后Mario Schweizer完成对比实验：在开关频率8 kHz、输出功率10 kW情况下，Conergy NPC逆变效率可达99.0%，且在8～15 kHz范围内高于传统二极管NPC逆变效率［5］。但Conergy NPC依然存在中点电位不平衡问题［6］。

目前，解决中点电位的问题一般采用硬件与软件方法，由于不增加成本，软件方法更加具有吸引力［7］，但应用于单相全桥Conergy NPC的软件方法较少。单相并网应用中，网侧与逆变器侧都通过电流传感器实现功率计算与电流环控制，过多的传感器将增加成本，影响可靠性［8，9］，根据节点电流定律，逆变器侧电流的信息由网侧电流与滤波电容电流合成，获取滤波电容中各次谐波信息，可估计出逆变器侧电流。谐波检测算法中，单一谐波分量采用快速傅里叶转换，但该算法存在频谱泄露和栅栏效应，实时响应性能差［10］的缺点；克尔曼滤波器、最小二乘方算法［11，12］对数学模型精度要求高，计算量大；改进型数字锁相环［13］通过跟踪被锁信号变化，能有效地滤除噪音与其他谐波干扰，谐波估计精准，但需经多个周期锁相环达到稳定，影响动态性能。

针对上述问题，本文参照三相NPC的软件平衡策略，研究了一种基于动态控制参数的单相全桥Conergy NPC中点平衡策略；详细介绍基于Luenberger状态观测理论的谐波观测器算法，实时精确估计出逆变器侧电流，并用于解决单相全桥Conergy NPC中点电位不平衡问题。

1　单相全桥Conergy NPC

1.1数学模型

单相全桥Conergy NPC拓扑，每一相桥臂有3种输出状态，Sx、Tx分别表示x相的开关状态和开关管导通状态，括号中1、0表示开关导通、关断，uab为逆变器侧输出线电压，Udc为直流侧输入电压。则

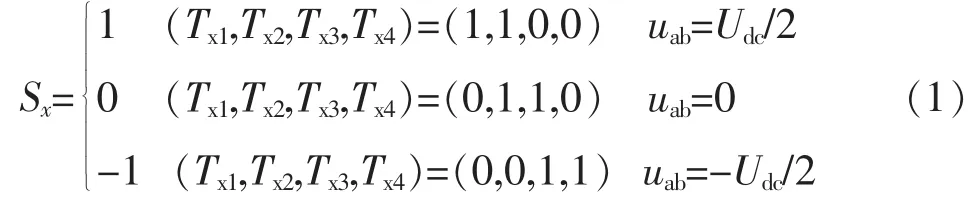
根据式（1）可得出单相全桥Conergy NPC开关模型，如图1所示。其中LC为忽略内阻的理想滤波环节，Uc1、Uc2为直流侧电容C1、C2的电压，开关状态与输出线电压的关系表示为uab=（Sa-Sb）ubc。

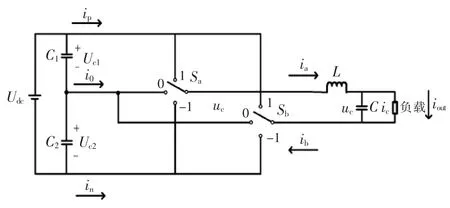
图1　单相全桥Conergy NPC开关模型Fig.1 Switch model for single phase Conergy NPC

根据基尔霍夫电流定律，图1中点电流i0、正极输出电流ip、负极输出电流in与平衡电容电压之间关系为

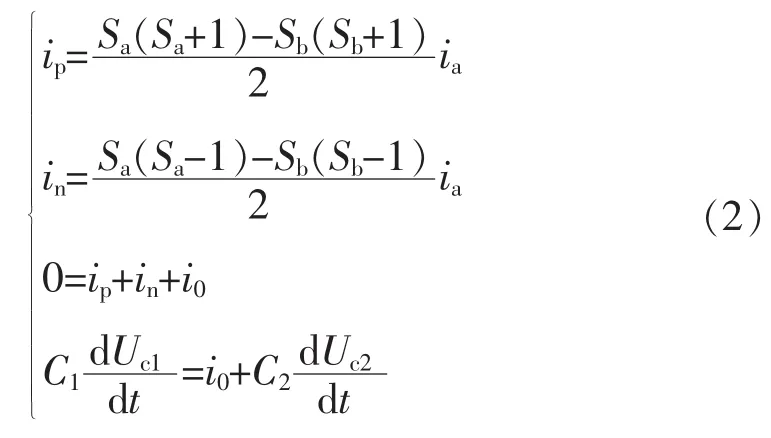
实际应用中，平衡电容C1=C2=C，中点电位波动ΔU仅由两桥臂的开关函数与输出相电流ia决定，即

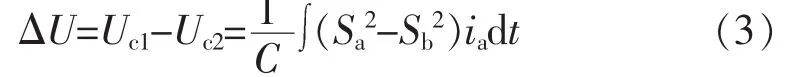
根据式（3），当开关状态为（1，0）和（-1，0）时，输出线电压相等，开关函数（1，0）引起的中点波动与（-1，0）所引起的中点波动相反；同理，开关函数（0，1）与（-1，0）也具有相同性质。因此当中点电位出现不平衡时，可以通过调节上述4个开关状态时间，平衡中点电位。

1.2SVPWM调制策略

定义开关矢量为（Sa，Sb），其分布于αβ坐标系的α坐标轴上5个固定位置，整个坐标系被划分为4个区域，见图2（a）。其中，Vref为逆变器输入电压参考矢量，θ为相位角，虚线圆为Vref在αβ坐标系内沿着逆时针旋转的轨迹；Vin为Vref在α坐标轴上的投影，见图2（b）。单相SVPWM调制实际上是一种直线矢量合成方式，根据第1.1节分析，在矢量合成时，为了减少中点电位的波动，开关矢量（1，0）与（0，-1）作用时间相同，（0，1）与（-1，0）作用时间相同；同一开关周期中禁止Sx在1与-1之间直接切换。综合上述规则，SVPWM策略采用5矢量合成方法［14］，有效减少开关谐波。其中5矢量合成顺序所对应的矢量时间为Ta/4→Tb/2→Ta/2→Ta/4→Tb/ 2→Ta/4，开关函数完成矢量合成，5矢量合成单相SVPWM策略如表1所示。

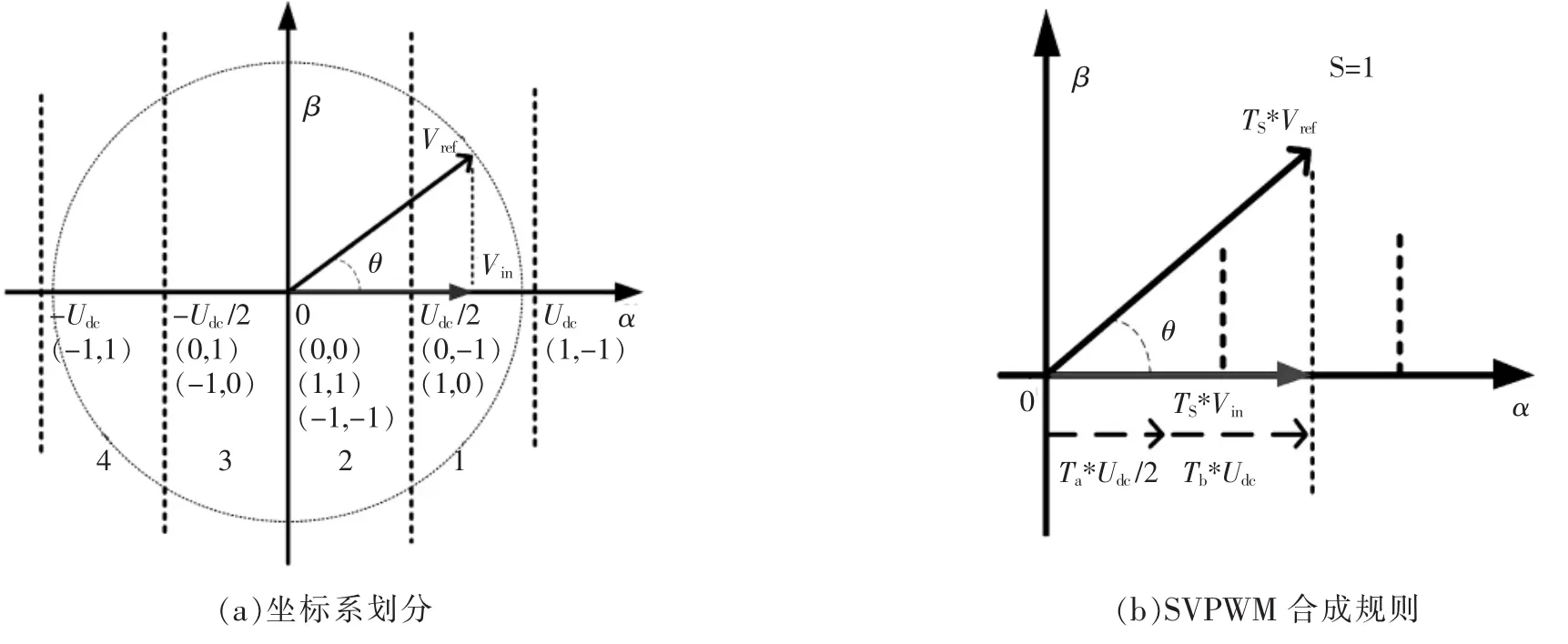
图2　单相SVPWM调制Fig.2 Space vectors modulation for single phase

表1　5矢量合成单相SVPWM策略Tab.1 Five vectors single-phase SVPWM strategy

1.3中点电压平衡策略

理想情况下，单相SVPWM调制的中点电位为0，但由于元器件的非理想性、负载非线性等问题［15］，不平衡问题依然存在。对单相Conergy NPC拓扑而言，T1、T2开关管在正常运行时所需承受最大管压降为直流侧输入电压［16］，一旦不平衡电压超过一定程度容易烧毁开关管。

考虑式（3），开关矢量（1，0）与（0，-1）为1对互补矢量，它们在一个开关周期中作用时间之和为Ta。在理想情况下，设矢量（1，0）作用时间为Ta+=Ta/2，设矢量（0，-1）作用时间为Ta-=Ta/2。同理，矢量（0，1）作用时间为Ta+，矢量（-1，0）作用时间为Ta-。根据表1与式（3）中4个开关矢量特点，引入动态控制参数λ，估计与补偿相结合，实时调节互补矢量作用时间，实现中点电位平衡。λ与开关矢量作用时间之间关系为

将中点电位波动参考值ΔU*与式（4）一同代入式（3），可以估计出下一开关周期中Ta的时间分配，即

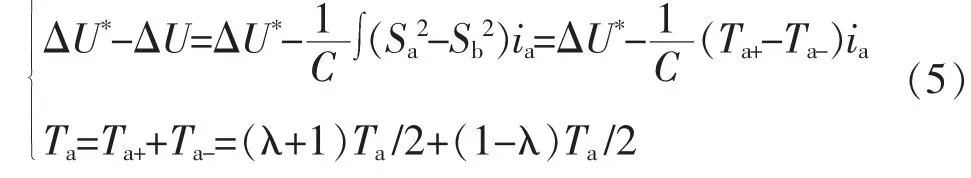
采样C1、C2上电压与逆变器侧输出电流ia可精确估计λ，即

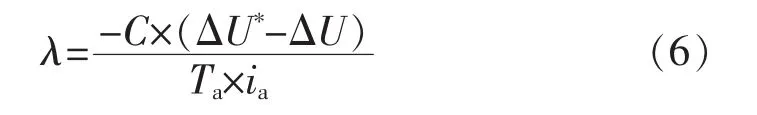
将λ参数代入式（4），通过单相SVPWM调制，补偿此时中点电位的不平衡。

2　谐波观测器算法设计

动态控制参数λ的估计，需要实时获取逆变器输出侧ia数值。图1中，ia（t）可表示为

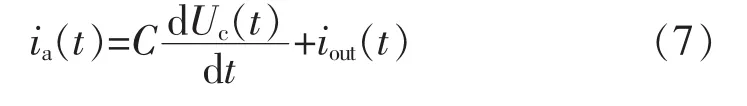
无法直接获取。本文设计一种谐波观测器算法，实时观测输入信号中各次谐波信息，同时产生各个谐波的正交信号，完成ia（t）的观测。

2.1待观测值数学模型

逆变器稳态工作时，输出电容电压uc（t）为非正弦周信号，用傅里叶级数可分解为直流分量、基波与高次谐波分量，即

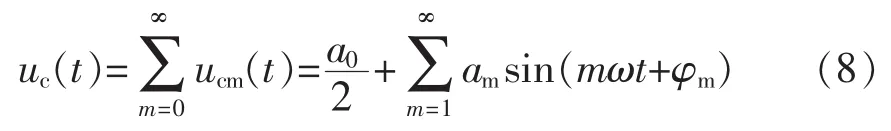
式中，ucm（t）为uc（t）信号中角频率m倍基波的正弦分量（m=0，1，2，3，…，∞）；am为分量信号的幅值大小。根据所观测信号的特点，设ucm（t）空间状态为

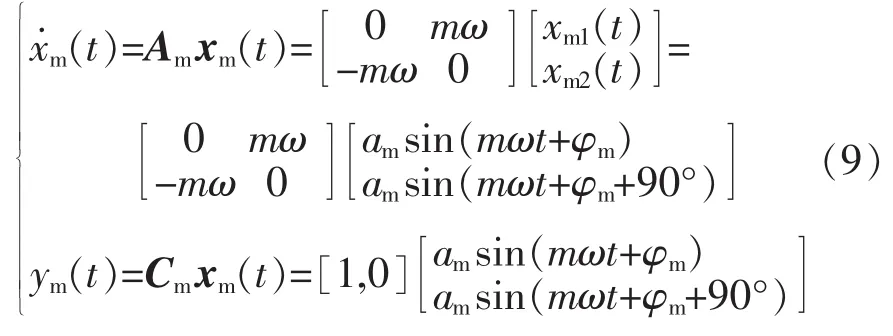
式中：xm（t）为状态矢量，其中xm1（t）=ucm（t），xm2（t）=；ym（t）为输出值；ucm（t）的空间矢量模型满足能观条件［17］；Am为系统矩阵，Cm为输出矩阵。

考虑微处理器使用离散信号，采样周期为T，对式（9）进行离散化，即

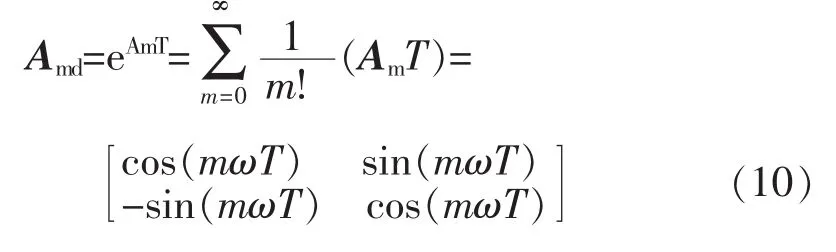
得到ucm（t）的离散模型ucm（kT）为

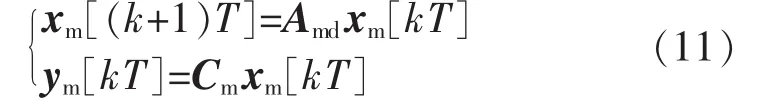
根据式（8）和式（11），uc（kT）可由ucm（kT）模型叠加而成，其空间表达式为

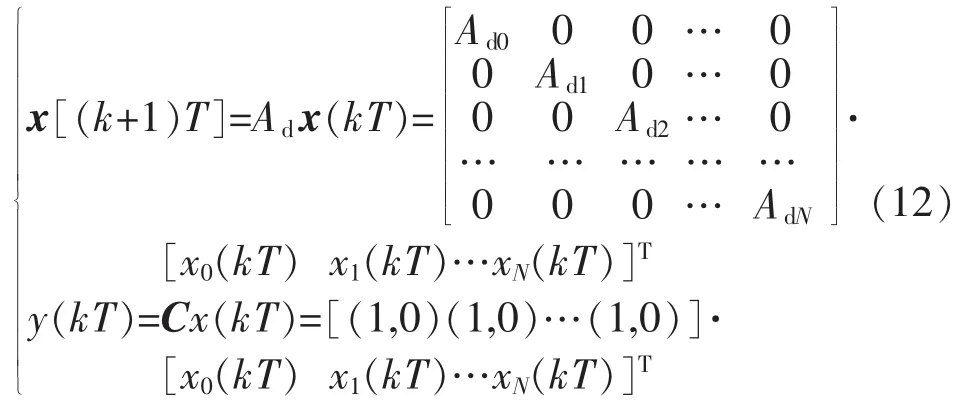
式中：x（kT）为状态矢量，由N个xm（kT）组成，大小为2N×1；y（kT）为输出值；Ad为uc（kT）的系统矩阵，大小为4N×4N；C为输出矩阵，大小为1×2N。

2.2观测器的设计

根据观测器设计原理，式（9）的对应观测器ucm（kT）空间状态表达式为

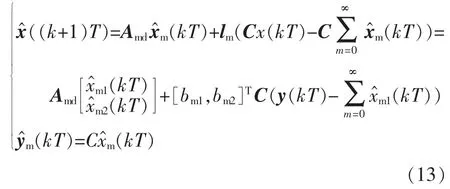
式中：lm为反馈矩阵；xm（kT）为xm（kT）的状态估计值，xm1（kT）为ucm（kT）的估计值，xm2（kT）为ucm（kT）正交值的估计值；ym（kT）为输出值。按照渐进观测的设计思路，输入信号uc（t）的离散观测器uc（kT）设计为一种闭环的观测器，其中的N个ucm（kT）子模块用

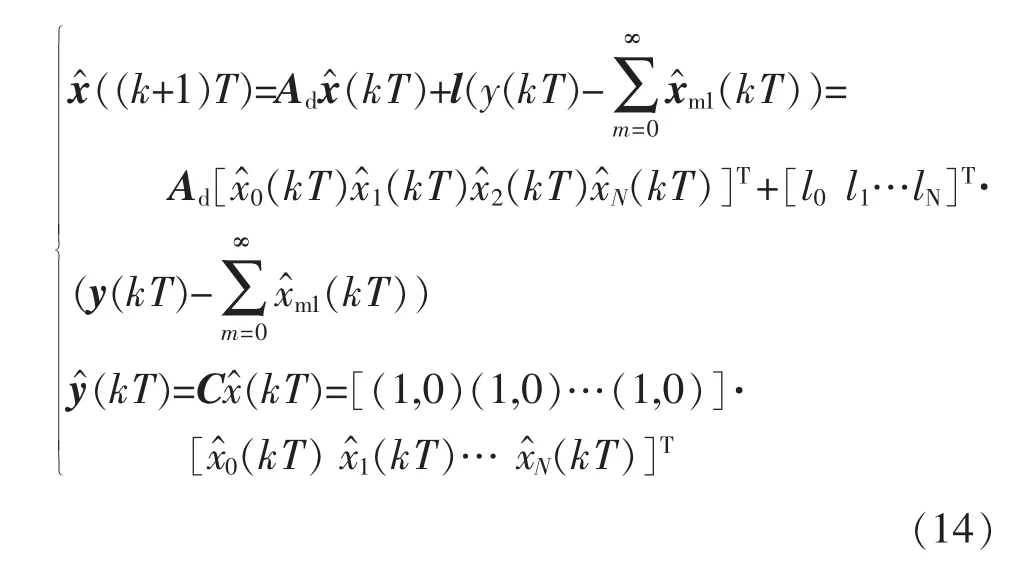
式中：l为反馈矩阵，它由N个lm组成；x（kT）为x（kT）的状态估计值；y（kT）为输入值uc（kT）的估计值；x（kT）为渐进误差，表示中趋近于ucm（t）的渐进速度；根据极点配置理论，为了满足（kT）=0，特征方程理想极点定义为zm1，m2=e-amTe±mωT，其中amT为理想极点距离z域中心圆的距离，控制amT的参数调节观测器的收敛速度、观测带宽与精度。x（kT）的差分方程为

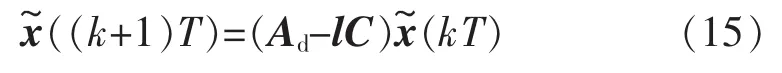
式（15）在z域中的特征方程为

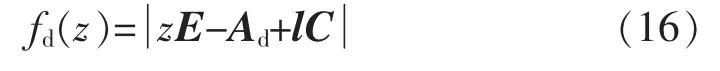
式中：E为2N×2N的单位矩阵；z为uc（kT）的极点数，z=2N。则期望的特征多项式定义为

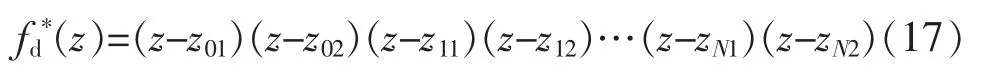
式（16）与式（17）系数相等，便可确定l的参数。

2.3观测器算法的验证

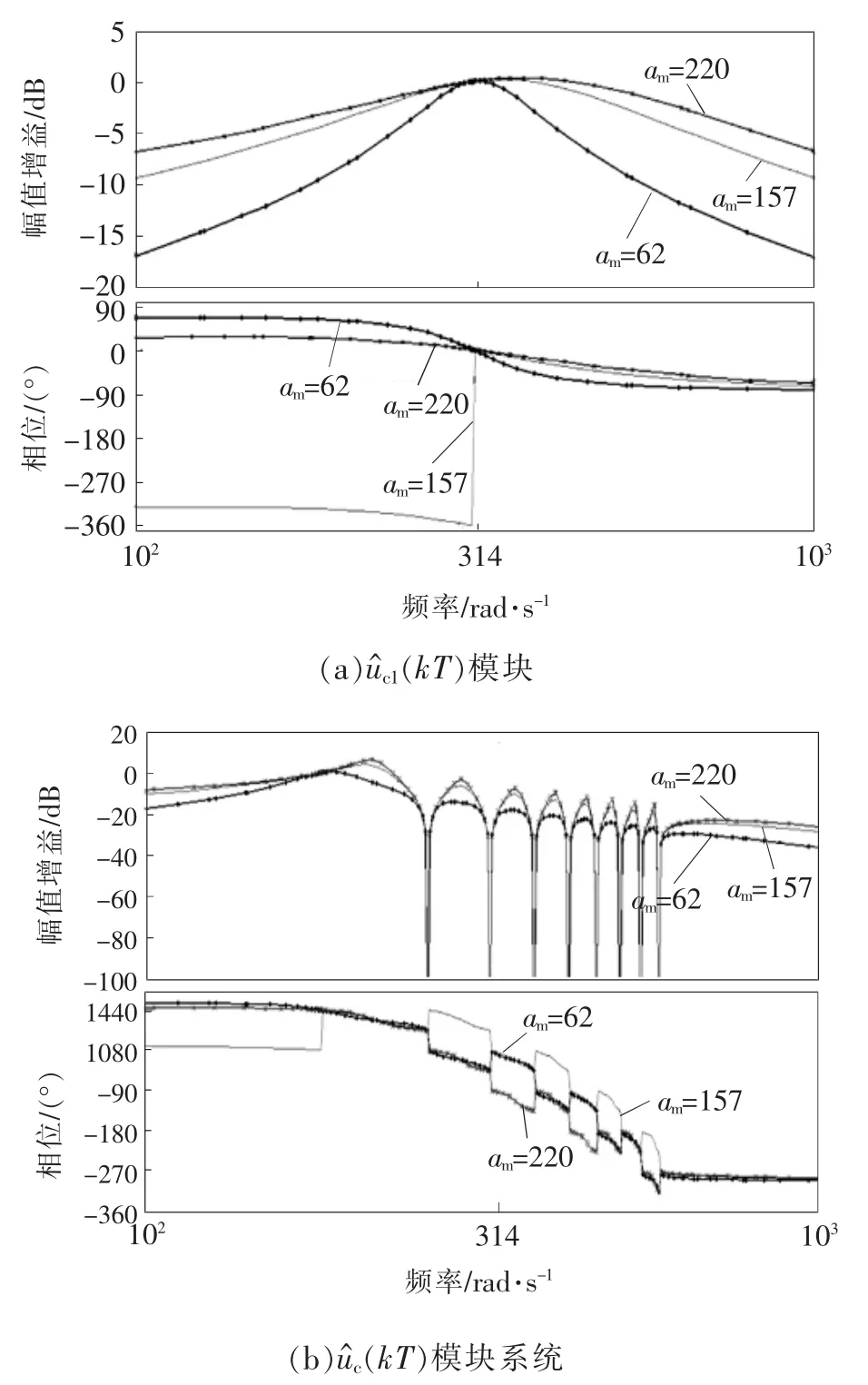
图3　频域特性Fig.3 Frequency-domain charateristics

根据第2.2节分析，在z域中，设am的3种不同取值分别为62、157、220，用于讨论极点位置对于观测器性能影响。根据式（16）、式（17），将3种am对应的反馈矩阵l代入式（14）中，得到3种l下的选用kT）中的）作为的输出，根据频域特性分析法，可以得到3种am的取值所对应的频域特性Bode图，如图3所示。图3（a）中，单独的模块相当于带通滤波器，随着am的减小，带宽逐渐减小。图3（b）中，对于所要估计频率的信号的增益为0 dB，相位偏移量接近于0°，其他信号分量频段进行-140 dB衰减。以不同频率模块的具体频域特性数据如表2所示。由图3可见，当am接近基频时，观察频段带宽较大，容易导致附近谐波放大。随着am的减小接近0，观测器的所要观察频段带宽减小，附近频率信号衰减力度增加，由此对系统的观测精度要求更高。根据以上数据结果，可以在原理上确定该观测器算法可行性。

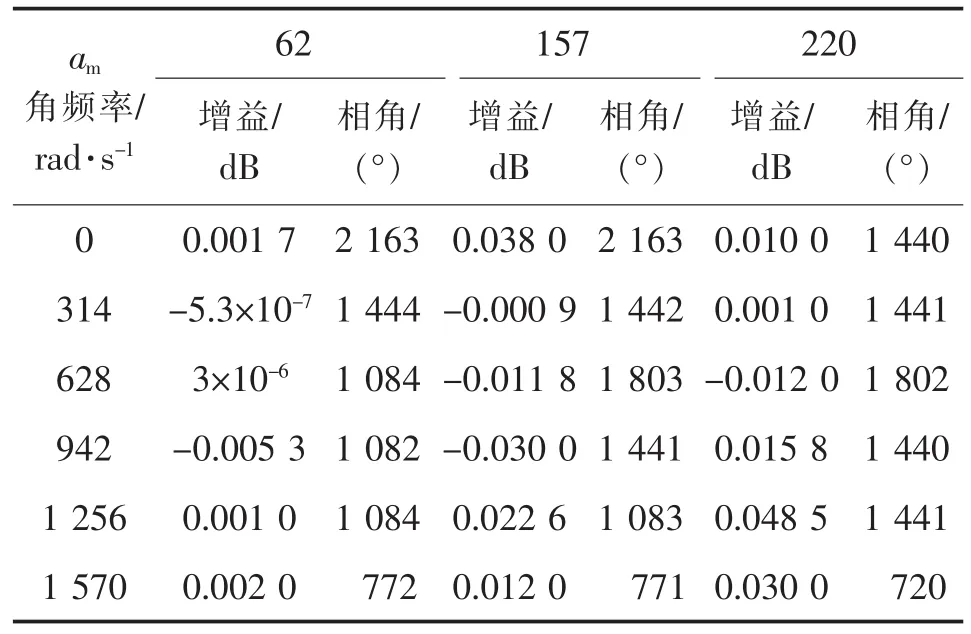
表2　频域特性Tab.2 Frequency-domain characteristics

3　仿真验证

为了验证上述观测器算法与中点平衡策略的正确性，在Matlab仿真平台上，首先应用谐波观测器对电感电流估计效果进行测试，然后将观测器算法应用于中点平衡策略进行实验验证。单相全桥Conergy NPC正常工作在逆变状态时，偶次谐波输出极少［18］，只需对输出电容电压uc（kT）的1，3，5，…，23奇次谐波进行观测。根据式（16）与式（17），可设计观测器模型，如图4所示。图（a）为（m=0，1，…，23）为m次谐波分量观测器，图（b）为子模块观测器结构。其仿真波形如图5所示。

为了验证谐波观测器算法效果与中点平衡策略，采用单相不控整流器充当非线性负载。图1中，电感参数为2 mH，电容为15 μF，Udc=650 V，不控整流输出滤波电容为10 μF，不控整流输出电阻为10 Ω，直流侧平衡电容为C1=C2=660 μF。将图4中电容电流的估计值代入式（7），得到电感电流的估计值为

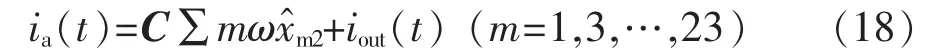
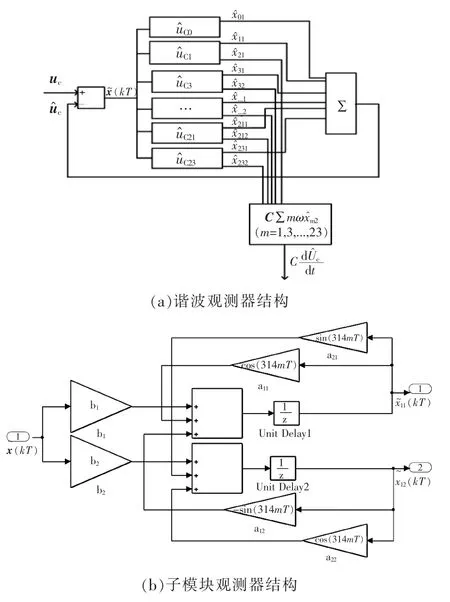
图4　谐波观测器模型结构Fig.4 Structures of harmonic observer model

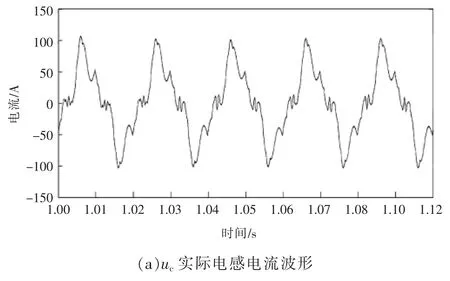
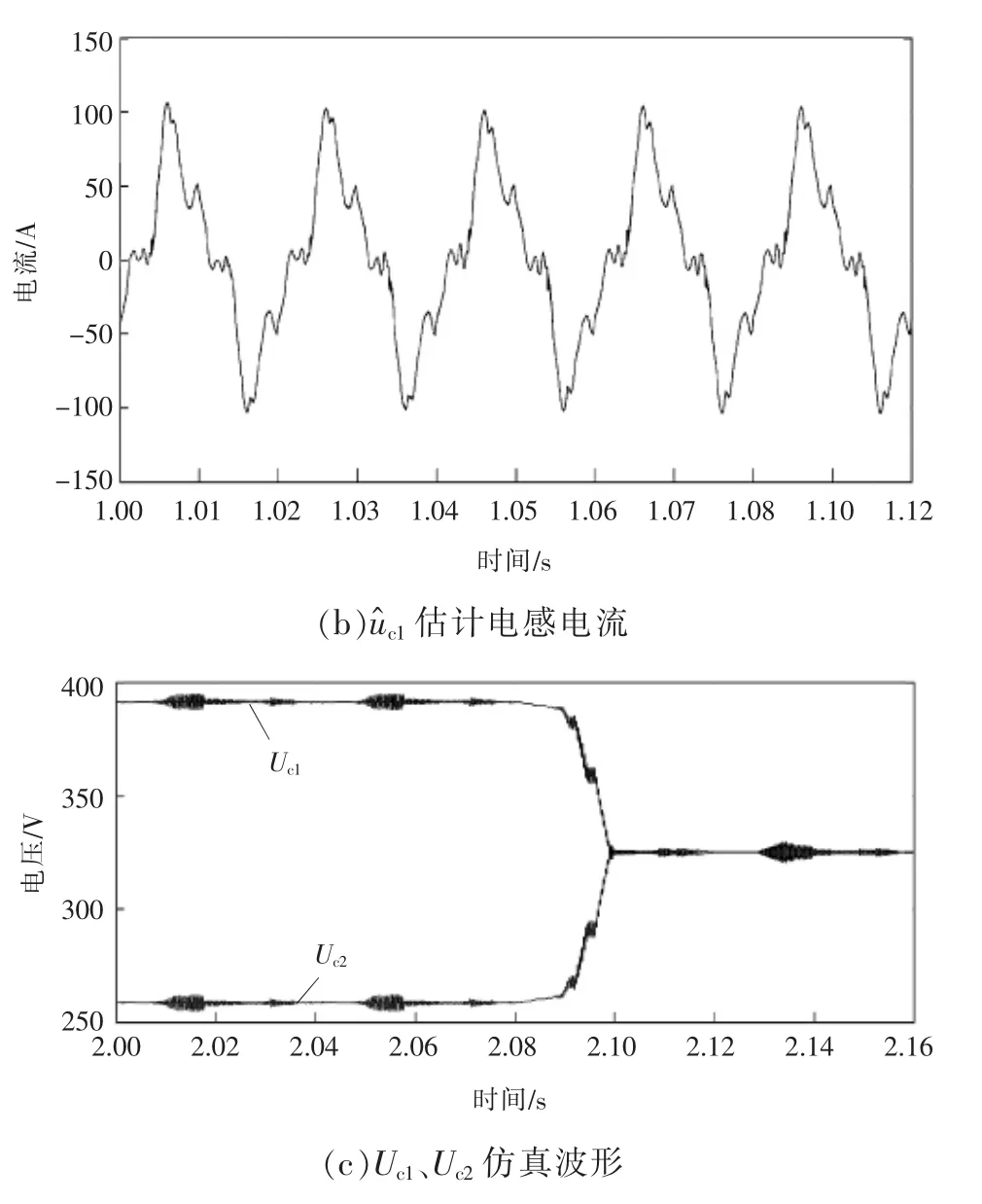
图5　仿真波形Fig.5 Simulation waveforms

由图5（a）、（b）可以看出，使用谐波观测器估计的电感电流在相位与幅值方面都与实际电感电流基本一致。将谐波观测器算法用于单相全桥Conergy NPC中点平衡策略，Uc1、Uc2仿真波形如图5 （c）所示。在非线性负载条件下，于2.08 s时加入中点电位平衡策略，经过0.02 s后中点电位迅速趋于平衡，由于单相全桥Conergy NPC调制矢量中不存在额外的不平衡矢量，所以平衡电位之后，整个中点波动较小。仿真结果可以验证本谐波观测器算法与中点平衡策略结合，能在较短时间内修复中点电位不平衡问题。

4　实验验证

以DSP28335为控制器，结合CPLD的SVPWM调制，搭建单相全桥Conergy NPC实验装置，进行验证。硬件测试分为谐波观测器算法和单相SVPWM算法与基于谐波观测器中点电位平衡策略验证。

4.1谐波观测器算法验证

谐波观测器由6个子模块构成（m=0，1，2，3，5，7），谐波观测器的观测结果见图6。观测器反馈矩阵参数为：l=［（0.0311，0）T，（0.0311，0.0068）T，（0.0311，0.0019）T，（0.0124，-0.0017）T，（0.0124，-0.0017）T，（0.0122，-0.0026）T］T

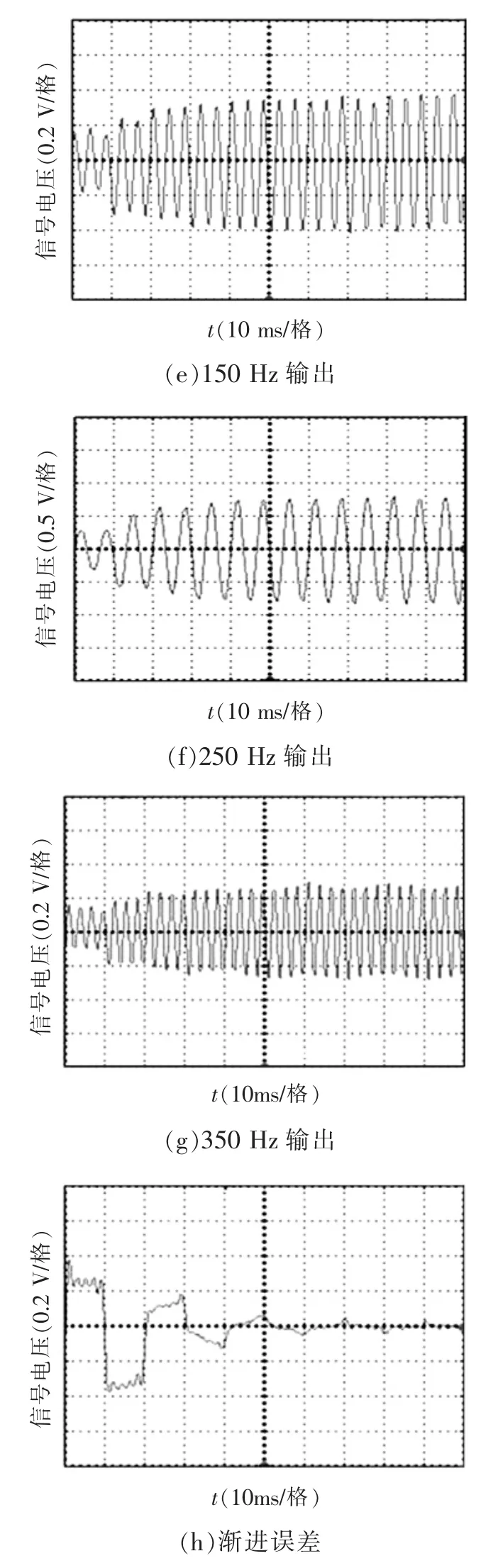
图6　DSP输出波形Fig.6 Output waveforms for DSP

输入测试信号为50 Hz、幅值为［0，3］的方波。在0.02 s时刻，观测值达到实际值的80%；在0.04 s时刻观测值达到实际值的95%。当观测器运行在稳态状态时，输入误差近乎于0。在DSP实际应用中（CPU主频率为150 MHz），6个开环模块组成谐波观测器，使用3 μs进行运算，对于采样周期为100 μs，谐波观测器所占用运算资源少，有充裕的资源完成其他控制算法。

4.2基于谐波观测器的中点平衡策略验证

采用8个FGA25N120 IGBT搭建单相全桥Conergy NPC实验装置，开关频率为10 kHz，滤波电感为3 mH，滤波电容为15 μF，直流输入电压Udc=280 V，直流侧输入平衡电容为C1=C2=660 μF。负载采用单相不控整流，不控整流输出电容为10 μF，并联电阻为10 Ω。谐波观测器由12个子模块构成（m=1，3，5，…，23），观测器反馈矩阵参数为：l=［（0.0125，8.5526e-4）T，（0.0125，-7.6104e-4）T，（0.0124，0.0017）T，（0.0122，-0.0026）T，（0.0121，-0.0034）T，（0.0121，-0.0041）T，（0.0115，-0.0049）T，（0.0112，-0.0056）T，（0.0108，-0.0063）T，（0.0410，-0.0268）T，（0.0410，-0.0281）T，（0.0372，-0.0319）T］T。逆变器侧输出波形如图7所示，Uc1、Uc2输出波形如图8所示。

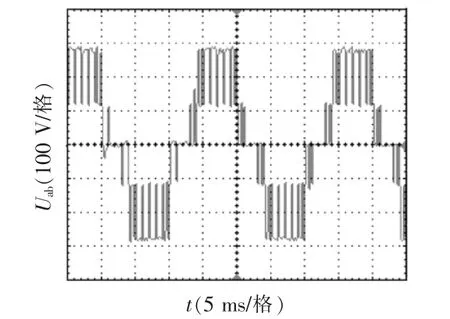
图7　Uc1、Uc2逆变器侧输出波形Fig.7 Line voltage waveform of inverter

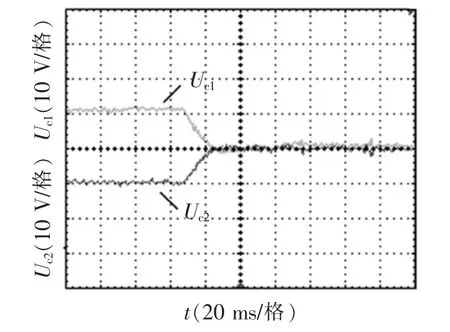
图8　Uc1与Uc2输出电压波形Fig.8 Output voltage waveforms forand

图7为逆变器的调制比为0.8时，Uab输出波形。图8中，当加入平衡策略时，大约花费0.04 s，中点电位恢复平衡，这是由于实际计算中λ参数有可能超过［-1，1］的范围，如此容易造成矢量配置的紊乱，使逆变器输出波形发生畸变，而且λ参数过大，平衡电容上电流变化会比较剧烈，会影响平衡电容的寿命。所以在实际应用中，应当限制参数在［-0.5，0.5］之间。

5　结语

本文研究了单相全桥Conergy NPC的中点平衡策略与一种基于状态观测器理论的谐波观测器算法的设计方法。采用谐波观测器对逆变器侧电流进行实时估计，并将其应用于中点平衡策略之中，对谐波观测器的实时估计性能与中点平衡策略的平衡能力进行进行了理论与实际性能的研究。在Matlab仿真与单相全桥Conergy NPC实验装置上都验证了基于谐波观测器的Conergy NPC单相逆变器中点平衡策略的可行性与有效性。此谐波观测器算法在实际应用中具有运算时间短、收敛时间快、观测精度高等特点，后续将在并网、电机控制、有源滤波等对谐波有所限制的领域深入研究。

［1］徐德鸿，陈文杰，何国锋，等.新能源对电力电子提出的新课题［J］.电源学报，2014，12（6）∶4-9. Xu Dehong，Chen Wenjie，He Guofeng，et al. New power electronics topics brought by the development of renewable energy［J］. Journal of Power Supply，2014，12（6）∶4-9 （in Chinese）.

［2］余新才，彭昌勇，施通勤，等. CRH2型电力机车建模与谐波电流分析［J］.武汉大学学报（工学版），2012，45（2）∶107-110. Yu Xingcai，Peng Changyong，Shi Tongqin，et al. Modling and analysis of harmonic currents of type CRH2 electric locomotive［J］. Engineering Journal of Wuhan University，2012，45（2）∶107-110（in Chinese）.

［3］马琳，孙凯，Remus Teodorescu，等.高效率中点钳位型光伏逆变器拓扑比较［J］.电工技术学报，2011，26（2）∶108-114. Ma Lin，Sun Kai，Remus Teodorescu，et al. Comparison of the topologies of high efficency neutral point clampingphotovoltaic inverters［J］. Transactions of China Electrotechnical Society，2011，26（2）∶108-114（in Chinese）.

［4］Knaup P. Inverter∶US20090003024A1［P］. 2009-01-01.

［5］Schweizer M，Kolar J W. Design and implementation of a highly efficient Three-Level T-Type converter for Low-Voltage applications［J］.IEEE Transactions on Power Electronics，2013，28（2）∶899-907.

［6］吴馥云，吕建国，胡文斌.一种变载波偏置的三电平中点电压平衡控制［J］.电源学报，2014，4（4）∶76-82. Wu Fuyun，Lv Jianguo，Hu Wenbin.Variable carrier offset control to balance the neutral-point voltage for three-level inverters［J］. Journal of Power Supply，2014，4（4）∶76-82（in Chinese）.

［7］姜卫东，杨柏旺，黄静，等.不同零序电压注入的NPC三电平逆变器中点电位平衡算法的比较［J］.中国电机工程学报，2013，33（33）∶17-25. Jiang Weidong，Yang Bowang，Huang Jing，et al. Comparisons of the neutral point voltage balancing algorithm for NPC three-level inverters based on different zero-sequence voltage injection［J］.Proceedings of the CSEE，2013，33（33）∶17-25（in Chinese）.

［8］张中锋.微网逆变器的下垂控制策略研究［D］.南京：南京航空航天大学，2013. Zhang Zhongfeng. Research on droop control strategey for microgrid inverter［D］.Nanjing∶Nanjing University of Aeronautics and Astronautics，2013（in Chinese）.

［9］郜登科，姜建国，张宇华.使用电压—相角下垂控制的微电网控制策略设计［J］.电力系统自动化，2012，36（5）∶29-34. Gao DengKe，Jiang Jiangguo，Zhang Yuhua. Design of mircrogrid control strategy using voltage amplitude and phase aangle droop control［J］.Automation of Electric Power Systems，2012，36（5）∶29-34（in Chinese）.

［10］George T A，Bones D. Harmonic power flow determination using the fast Fourier transform［J］. IEEE Transactions on Power Delivery，1991，6（2）∶530-535.

［11］Wahbi A. Enhancing the quality of voice communications by acoustic noise cancellation using a low cost adaptive algorithm based Fast Fourier Transform and circular convolution［C］. Morocco，9th International Conference on Intelligent Systems∶Theories and Applications，2014∶1-7.

［12］祝石厚.基于卡尔曼滤波算法的动态谐波状态估计技术研究［D］.重庆：重庆大学，2008. Zhu Shihou. Study on Dynamic Harmonic State Estimation Technology Based on Kalman filter［D］. Chongqing∶Chong qing University，2008（in Chinese）.

［13］Karimi-Ghartemani M S A，Jain P，Bakhshai A. A new phase-locked loop system for three-phase applications［J］. IEEE Transactions on Power Electronics，2013，28（3）∶1208-1218.

［14］宋文胜，冯晓云.一种单相三电平SVPWM调制与载波SPWM内在联系［J］.电工技术学报，2012，06（6）∶131-138. Song Wensheng，Feng Xiaoyun. Relationship between single phase three-level SVPWM and carrier SPWM［J］. Transactions of China Electrotechnical Society. 2012，6（6）∶131-138（in Chinese）.

［15］王顺亮，宋文胜，冯晓云.一种负载不平衡情况下单相三电平脉冲整流器中点电位控制方法［J］.电力自动化设备，2013，33（10）∶79-85. Wang Shunliang，Song Wensheng，Feng Xiaoyun. Neutral point voltage control for single-phase three-level pulse rectifier with unbalanced loads［J］. Electric Power Automation Equipment，2013，33（10）∶79-85（in Chinese）.

［16］王文，罗安，黎燕，等.一种新型有源电力滤波器的SVPWM算法［J］.中国电机工程学报，2012，18（18）∶52-58. Wang Wen，Luo An，LI Yan，et al. A novel algorithm of SVPWM applied to active power filters［J］. Proceedings of the CSEE，2012，18（18）∶52-58.（in Chinese）.

［17］Miskovic V，Blasko V，Jahns T，et al. Observer based active damping of LCL resonance in grid connected voltage source converters［C］. Canada∶IEEE Energy Conversion Congress and Exposition，2013∶15-19.

［18］Azeez N A，Gopakumar K，Mathew J，et al. A harmonic suppression scheme for open-end winding split-phase IM drive using capacitive filters for the full speed range［J］. IEEE Transactions on Industrial Electronics，2014，61（10）∶5213-5221.

Neural-point Balance Strategy for Conergy NPC Single-phase Inverter Based on Harmonic Observer

YI Lingzhi1，2，HUANG He1，LI Weiping3，CHEN Caixue1，2，CHEN Renkai1
（1.Key Laboratory of Intelligent Computing & Information Processing，Xiangtan University，Ministry of Education，Xiangtan 411105，China；2.Wind Power Equipment and Power Conversion 2011 Collaborative Innovation Center.，Xiangtan 411105，China；3.Department of Electronic Science，Huizhou University，Guangzhou 516007，China）

An algorithm of harmonic observer of various harmonic contents is proposed for real-time estimation in cycle nonsinusoidal signal，which be applied to neutral point balance strategy. This paper introduces the neutral-point balance strategy based on dynamic control parameters after analyzing the switch model of single phase full-bridge Conergy NPC and space vector pulse width modulation（SVPWM）modulation methods. A harmonic observer for the capacitance and voltage of filtering，based on state observer theory，is designed in order to get information about harmonic signal and orthogonal signal from sampling signal.Meanwhile，the observed information will also be applied to the neutral point balance strategy. Both simulation experiments and hardware experiments verify the feasibility and validity of this balance strategy based on neutral-point potential in harmonic observer.

Conergy NPC；dynamic control parameter；neutral-point balance strategy；harmonic observer

易灵芝

2015-06-03

国家自然科学基金“基于自动需求响应的多能互补智能楼宇全直流微网动态优化”（61572416）；湖南省教育厅平台项目“小功率新型开关磁阻风力发电装备制造中关键技术研究”（14K095）；湖南省“十二五”重点学科“信息与通信工程”资助项目

易灵芝（1966-），女，通信作者，硕士，教授，研究方向：交流调速与电力电子装置，新能源发电与直流微网等，E-mail：ylz wyh@sohu.com。

黄鹤（1990-），男，硕士研究生，研究方向：新能源发电技术，E-mail：314323089 @qq.com。

李卫平（1968-），女，副教授，研究方向：新能源发电，E-mail：dzx@hzu.edu.cn。

陈才学（1979-），男，博士，副教授，研究方向：电力电子，E-mail：cyyccx@126.com。

陈人楷（1992-），男，本科，研究方向：多电平应用技术，E-mail：1879521232@qq. com。