适用于声波方程数值模拟的时间-空间域隐式有限差分算子优化方法

陈东， 梁文全， 辛维*， 杨长春

1 中国科学院地质与地球物理研究所， 中国科学院油气资源研究重点实验室， 北京 100029 2 胜利油田分公司东胜精攻石油开发集团股份有限公司， 山东东营　257000

适用于声波方程数值模拟的时间-空间域隐式有限差分算子优化方法

陈东1,2， 梁文全1， 辛维1*， 杨长春1

1 中国科学院地质与地球物理研究所， 中国科学院油气资源研究重点实验室， 北京 100029 2 胜利油田分公司东胜精攻石油开发集团股份有限公司， 山东东营257000

摘要声波方程数值模拟已广泛应用于理论地震计算，同时构成了地震逆时偏移成像技术的基础.对于有限差分法而言，在满足一定的稳定性条件时，普遍存在着因网格化而形成的数值频散效应.如何有效地缓解或压制数值频散是有限差分方法研究的关键所在.有限差分格式分为显式有限差分和隐式有限差分.隐式有限差分能够进一步压制数值频散效应.因此本文提出了给定频率范围满足时间-空间域隐式有限差分频散关系的方法，并根据震源频率、波速和网格间距确定波数范围，在此基础上建立方程确定了相应的隐式有限差分系数，使得差分系数能在更大频率范围符合波场传播规律.通过频散分析和正演模拟，验证了本文方法的有效性.

关键词声波正演； 时间-空间域； 隐格式有限差分； 频散关系

1引言

因为声波方程有限差分方法计算效率高、所需内存相对较小、实现简单，而广泛应用于地震正演研究(Alford, et al.，1974；Kelly, et al.，1976；Basabe and Sen，2007；冯英杰等，2007；王珺等，2007；韩令贺等，2011；兰海强等，2011；Chu and Stoffa, 2012a, 2012b; Wang, 2014)，同时也是地震逆时偏移成像技术得以快速发展的基础(李博等，2012;刘红伟等，2011,2012).

网格频散是有限差分中至关重要的问题，直接影响着有限差分法在波动方程数值解过程中的应用效果.网格频散是由对时间和空间偏导数网格化造成的，相速度变成了网格间距的函数(Dablain 1986)，这会导致地震波的数值相速度不等于地球介质的真实相速度，使得波场模拟的精度降低.一般来说，如果存在时间频散，则高频的相速度增大；如果存在空间频散，则高频的相速度减小(Dablain 1986).

为了缓解或者压制网格数值频散效应，一般采用两种措施：其一是采用低阶差分格式，要求时间步长和空间步长非常小，这会造成所需内存和计算量过大而无法应用于三维的情况；其二是采用高阶差分格式，一般情况下，时间方向采用二阶差分格式，空间方向采用高阶差分格式或伪谱法.高阶差分格式主要是利用等波纹准则或最小误差准则优化设计差分系数实现对空间偏导数的近似.伪谱法则是通过正、反傅里叶变换来实现空间偏导数的精确求解.两种方法相比，高阶空间差分格式具有精度适中、计算效率高的特征而得到广泛应用，特别是用于地震逆时偏移成像.伪谱法计算精度高，但因计算量过大，一般常用于地震正演模拟.此外，Dablain(Dablain 1986)和Chen(Chen 2007, 2011)提出了时间方向导数的四阶有限差分格式，提高了波场模拟的精度.

在空间方向偏导数差分格式近似计算方面已开展了大量研究工作，积累了大量的研究成果.考虑到在地震波场数值模拟中，需在时间方向和空间方向同时网格化，两者共同决定着数值频散特征.因此仅依靠空间方向偏导数计算精度的提高，并不能压制时间频散，甚至加强了时间频散.鉴于上述原因，Finkelstein提出了在时间-空间域内设计与确定有限差分格式的新方法，以期提高正演模拟计算精度.其方法原理是空间域对波数进行泰勒展开、特定频率点满足相速度关系、群速度关系的组合，用以控制精度的阶数和频散(Finkelstein and Kastner, 2006; Finkelstein and Kastner, 2008).

偏微分方程的有限差分格式分为显式的和隐式的.显式有限差分格式中，某点导数的计算需要该点和它周围点的值.隐式有限差分格式中，某点导数的计算除了需要该点和它周围点的值之外，还需要它周围点的导数值(Liu and Sen，2009).使用隐式有限差分格式需要求解多对角阵，因而计算量较大.但是为了达到相同的精度，使用隐式有限差分算子比使用显式有限差分算子一般需要更少的网格点.Liu和 Sen(2009)的研究指出，对于二阶导数来说，隐式差分格式(2N+2)阶有限差分算子的精度相当于(4N+2)阶显式有限差分算子的精度.但是传统的隐式有限差分有两个缺点：第一是在空间域进行泰勒展开求取有限差分系数，仅能在低频或者低波数较好的保持频散关系；第二是在空间域求取隐式有限差分系数，不能减小时间频散.因此，本文提出了使用线性化的方法在时间-空间域确定隐式有限差分算子，使得算子在更大的波数范围保持时间-空间域频散关系，从而提高正演模拟的精度和效率.

2方法

本文以一维声波方程为例分析差分格式的优化问题：

(1)

其中，p(x,t)是波场，v是纵波速度.

二阶导数的显式有限差分算子公式：

(2)

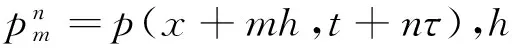
函数p(x,t)二阶中心差分：

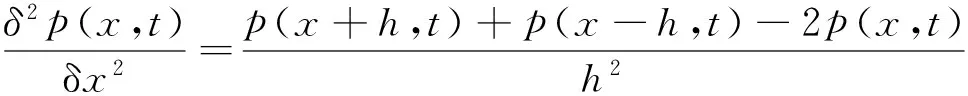
(3)

二阶导数的隐式有限差分算子公式为(Liu and Sen, 2009)

(4)

其中，cm(m=0,1,2,…,M)和b是隐格式有限差分系数.当b=0时，得到的是显式的二阶导数有限差分算子.

(5)其中，r=vτ/h， α=kh/2， ω=kv.

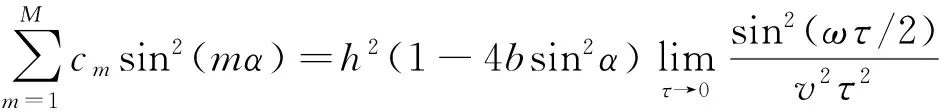
=(1-4bsin2α)α2,

(6)

则时间-空间域隐式有限差分格式退化为空间域隐式有限差分格式.

根据震源最高频率，波速和网格间距确定需要优化的波数上限(梁文全等, 2013)：

(7)

其中，f是最高震源频率.

在确定的波数范围内，选择M+1个均匀分布的波数点满足时间-空间域隐式差分格式有限差分算子频散关系(公式(5))，则得到下面的线性方程组：

(8)

解线性方程组，可以求得时间-空间域隐式有限差分算子的系数，其中

(9)

由公式(8)可见，时间-空间域隐式有限差分算子的系数与波速、所取波数范围、时间步长和空间步长有关.也就是说，时间-空间域中，对于不同的波速，隐格式有限差分的系数b是不同的.但是隐格式有限差分中，空间偏导数的求取需要解一个三对角阵，这个三对角阵主要有b构成，一般希望b值是固定的.同时我们知道，低波速需要的算子长度最长.因此根据最低波速确定b值，然后把b作为已知，求取系数cm(m=0,1,2,…,M).空间域隐格式有限差分算子，空间域交错网格隐格式有限差分算子，时间-空间域隐格式交错网格有限差分算子的推导与上述相同，不再赘述.

3频散分析

使用下面的公式衡量时间-空间域频散(Liu and Sen, 2009)：

(10)

δ的值越接近1，数值频散越小；否则数值频散越大.

由图1可以看到，随着有限差分算子长度的增加，传统隐式有限差分算子和时间-空间域隐式有限差分算子的数值频散都减小.时间-空间域新方法的数值频散在整个kh范围内分布比较均匀，在更广的kh范围内保持较小误差，且可以根据震源频率、空间步长调整需要满足频散关系的波数上限使得kh比较小的情况下数值频散也很小.

由图2和3可以看出，随速度和时间步长的变化，传统隐式有限差分算子的数值频散变化比较大，而时间-空间域隐式有限差分算子频散误差变化比较小，因此新方法比传统的方法稳定.

4正演例子

4.1均匀介质的二维声波正演

首先使用均匀介质模型，模型大小为220×200.对于所有的隐式有限差分算子M=8,v=2000 m·s-1,

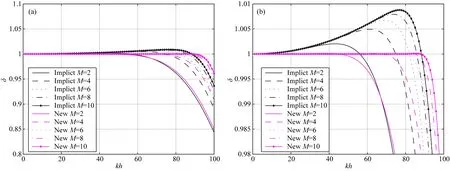
图1　两种不同方法随M增加的数值频散图(a) 频散对比； (b) a图的局部放大, 其中，v=2000 m·s-1时间步长h=10 m,空间步长τ=0.001 s.Fig.1　Plot of dispersion curves for different M (a) the comparison of FD dispersion; (b) zoom of (a)

图2　两种不同方法随M增加的数值频散图(a) 频散对比； (b) a图的局部放大； 其中，v=2000 m·s-1时间步长h=10 m,空间步长τ=0.002 sFig.2　Plot of dispersion curves for different M when τ=0.002 s (a) the comparison of FD dispersion; (b) zoom of (a)

图3　两种不同方法随M增加的数值频散图(a) 频散对比； (b) a图的局部放大；其中，v=4500 m·s-1时间步长h=10 m,空间步长τ=0.001 sFig.3　Plot of dispersion curves for different M when v=4500 m·s-1 (a) the comparison of FD dispersion; (b) zoom of (a)

h=10 m,时间步长 dt=1 ms.震源放在中心位置. 震源子波定义为

(11)

其中，f0=150 Hz，f0/π是震源主频,t0=4/f0，c是常数.

儒家思想之内涵、处事原则及方式，无不体现着对经与权的阐释。权，从字面意思来理解是变化，似乎与原则相悖，但却是对经的完美补充，于是便有君子之中庸，有经有权，小人反中庸。权，这一尺度生于人心权衡机能，生成固定之经后，又可以反过来帮助人在具体情境中进行尺度的判断和运用。

传统隐式有限差分格式和时间-空间域隐式有限差分格式在350 ms时的波场快照如图4所示.图4的切片(z/dz=110)如图5所示，我们以时间步长0.5 ms的伪谱法为解析解.由图4可见，伪谱法(τ=1 ms)的时间频散严重，传统的隐式差分格式时间频散和空间频散都严重，时间-空间域隐式有限差分格式同时有效压制了时间频散和空间频散.4.2Marmousi模型

图6显示了Marmousi模型，其速度在1500 m·s-1和4700 m·s-1之间.震源子波如公式 (11)所示，其中f0=120 Hz.对于不同的有限差分算子h=10 m, dt=1 ms,M=8.

图7a是空间域泰勒展开法隐式有限差分格式的地震记录，频散明显；图7b是时间-空间域隐式有限差分算子的地震记录, 时间和空间频散都得到压制.同时我们注意到，使用空间域隐式有限差分格式进行正演模拟的时候，在1000 ms时已经出现不稳定现象，数值模拟崩溃.而使用时间-空间域隐式有限差分格式则可以保持稳定.两种方法在x/dx=250处的地震记录如图8所示，新方法明显同时减小了时间频散和空间频散.

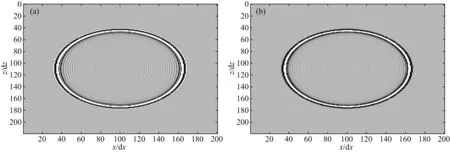
图4　传统隐式有限差分算子(a)和新时间-空间域有限差分算子(b)的波场快照Fig.4　Comparison of snapshots for the conventional implicit method and the new time-space domain implicit method

图5　图4的切片图Fig.5　Slice of snapshots in Fig.4

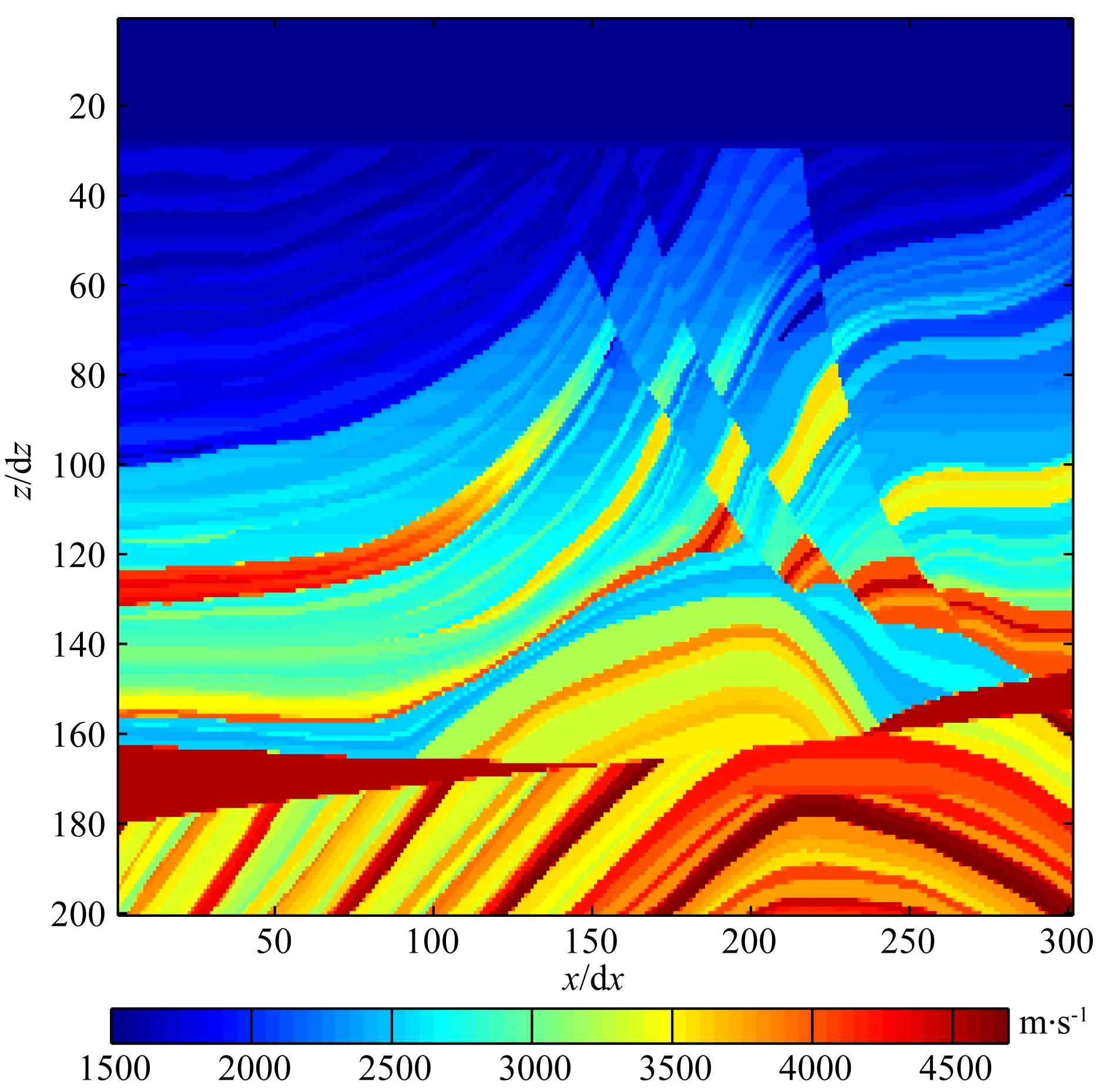
图6　Marmousi模型Fig.6　Marmousi velocity model

5结论

本文提出了时间-空间域确定声波方程隐式有限差分算子的准则，即给定波数范围满足频散关系.方法本身无需在波数方向上进行泰勒展开，而是通过震源频率、波速和网格间距确定波数上限，这使得新的差分格式在更大范围符合波场传播规律.此外，与传统的隐式有限差分格式相比，新的隐式有限差分格式稳定性更好.

图7　Marmousi模型地震记录(a) 传统方法隐式有限差分算子; (b) 时间-空间域隐式有限差分算子.Fig.7　Seismic records from the Marmousi model(a) The conventional implicit method; (b) The new time-space domain implicit method.

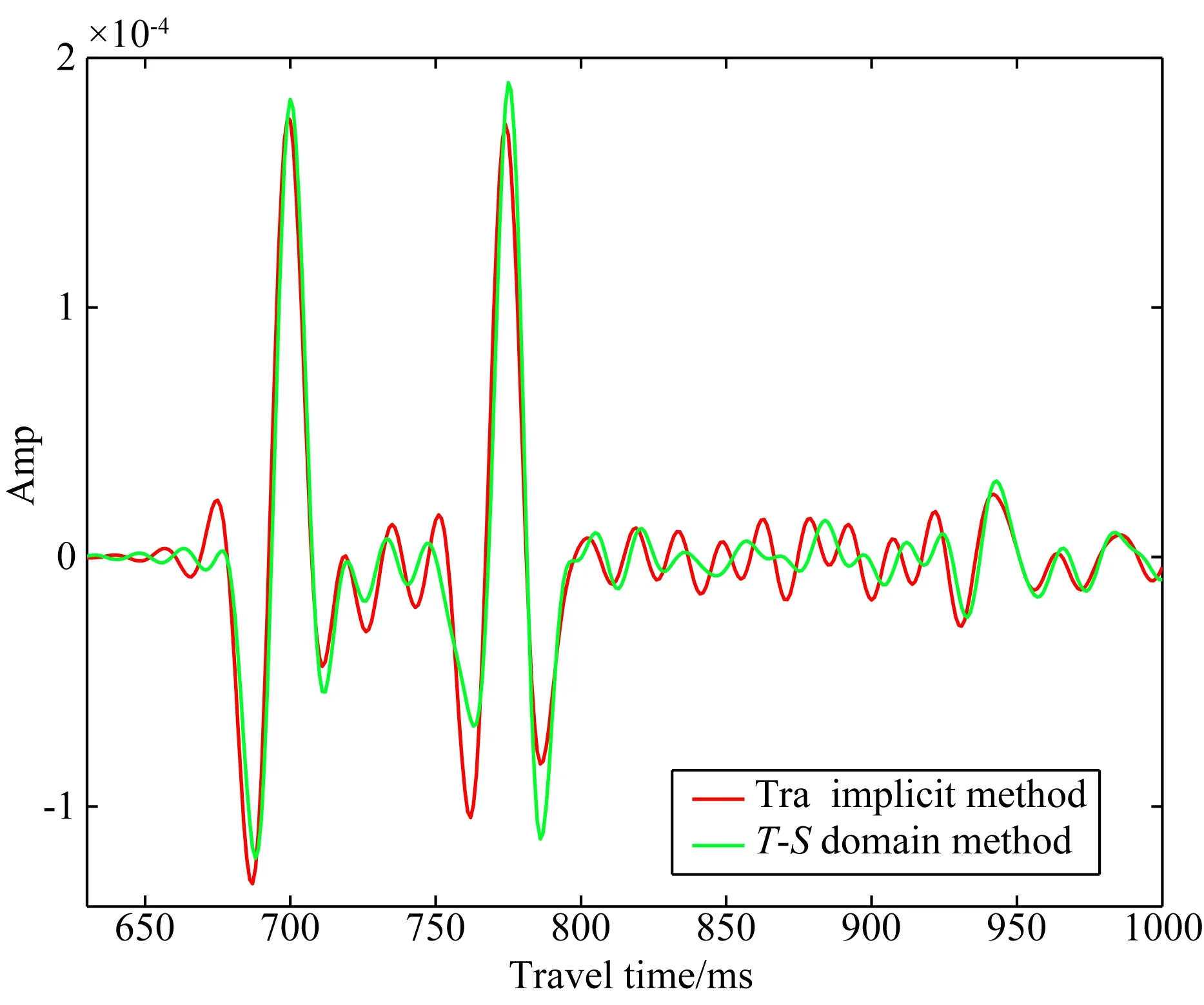
图8　Marmousi模型地震道对比红线表示传统隐式方法计算的地震道，绿线表示时空域隐式方法计算的地震道.Fig.8　Comparison of seismic seismograms from Marmousi model (the red line is the traditional implicit method, whereas the green line is the new time-space domain method).

通过频散分析，以及二维的地震波数值模拟，验证了本文提出的新方法的有效性.因此，时间-空间域隐式有限差分算子方法可以代替空间域泰勒展开法隐式有限差分算子用于地震的正演、逆时偏移中，以提高地震波数值模拟的精度和效率.

References

Alford R M, Kelly K R, Boore D M. 1974. Accuracy of finite-difference modeling of the acoustic wave equation.Geophysics, 39(6): 834-842.

Basabe J D D, Sen M K. 2007. Grid dispersion and stability criteria of some common finite-element methods for acoustic and elastic wave equations.Geophysics, 72: T81-T95. Chen J B. 2007. High-order time discretizations in seismic modeling.Geophysics, 72(5): SM115-SM122.Chen J B. 2011. A stability formula for Lax-Wendroff methods with fourth-order in time and general-order in space for the scalar wave equation.Geophysics, 76(2): T37-T42.

Chu C C, Stoffa P L. 2012a. Implicit finite-difference simulations of seismic wave propagation.Geophysics, 77(2): T57-T67.

Chu C C, Stoffa P L. 2012b. Determination of finite-difference weights using scaled binomial windows.Geophysics, 77(3): W17-W26.

Dablain M A 1986. The application of high-order differencing to the scalar wave equation.Geophysics, 51(1): 54-66.

Feng Y J, Yang C C, Wu P. 2007. The review of the finite-difference elastic wave motion modeling.ProgressinGeophysics(in Chinese), 22(2): 487-491.

Finkelstein B, Kastner R. 2008. A comprehensive new methodology for formulating FDTD schemes with controlled order of accuracy and dispersion.IEEETransactionsonAntennasandPropagation, 56(11): 3516-3525.Finkelstein B, Kastner R. 2006. Finite difference time domain dispersion reduction schemes.JournalofComputationalPhysics, 221(1): 422-438. Han L H, He B S, Zhang H X. 2011. Prestack reverse-time depth migration of quasi-P wave equations in VTI media.ActaSeismologicaSinica(in Chinese), 33(2): 209-218.Kelly K R, Ward R W, Treitel S, et al. 1976. Synthetic seismograms: A finite-difference approach.Geophysics, 41(1): 2-27.

Lan H Q, Liu J, Bai Z M. 2011. Wave-field simulation in VTI media with irregular free surface.ChineseJournalofGeophysics(in Chinese), 54(8): 2072-2084, doi: 10.3969/j.issn.0001-5733.2011.08.014.Li B, Li M, Liu H W, et al. 2012. Stability of reverse time migration in TTI media.ChineseJ.Geophys. (in Chinese), 55(4): 1366-1375, doi: 10.6038/j.issn.0001-5733.2012.04.032.

Liang W Q, Yang C C, Wang Y F, et al. 2013. Acoustic wave equation modeling with new time-space domain finite difference operators.ChineseJ.Geophys. (in Chinese), 56(10): 3497-3506, doi: 10.6038/cjg20131024.

Liu H W, Liu H, Zou Z, et al. 2010. The problems of denoise and storage in seismic reverse time migration.ChineseJ.Geophys. (in Chinese), 53(9): 2171-2180, doi: 10.3969/j.issn.0001-5733.2010.09.017.

Liu H W, Liu H, Li B, et al. 2011. Pre-stack reverse time migration for rugged topography and GPU acceleration technology.ChineseJ.Geophys. (in Chinese), 54(7): 1883-1892, doi: 10.3969/j.issn.0001-5733.2011.07.022.Liu Y, Sen M K. 2009. A practical implicit finite-difference method: examples from seismic modelling.JournalofGeophysicsandEngineering, 6(3): 231-249.Wang J, Yang C C, Feng Y J. 2007. Utilizing optimal flux-corrected transport technology to suppress dispersion simulation.ProgressinExplorationGeophsics(in Chinese), 30(4): 252-256.Wang Y F, Liang W Q, Nashed Z, et al. 2014. Seismic modeling by optimizing regularized staggered-grid finite-difference operators using a time-space-domain dispersion-relationship-preserving method.Geophysics, 79(5): T277-T285.

附中文参考文献

冯英杰, 杨长春, 吴萍. 2007. 地震波有限差分模拟综述. 地球物理学进展, 22(2): 487-491.

韩令贺, 何兵寿, 张会星. 2011. VTI介质中准P波方程叠前逆时深度偏移. 地震学报, 33(2): 209-218.

兰海强, 刘佳, 白志明. 2011. VTI介质起伏地表地震波场模拟. 地球物理学报, 54(8): 2072-2084, doi: 10.3969/j.issn.0001-5733.2011.08.014.

李博, 李敏, 刘红伟等. 2012. TTI介质有限差分逆时偏移的稳定性探讨. 地球物理学报, 55(4): 1366-1375, doi: 10.6038/j.issn.0001-5733.2012.04.032.

梁文全, 杨长春, 王彦飞等. 2013. 用于声波方程数值模拟的时间-空间域有限差分系数确定新方法. 地球物理学报, 56(10): 3497-3506, doi: 10.6038/cjg20131024.

刘红伟, 刘洪, 邹振等. 2010. 地震叠前逆时偏移中的去噪与存储. 地球物理学报, 53(9): 2171-2180, doi: 10.3969/j.issn.0001-5733.2010.09.017.

刘红伟, 刘洪, 李博等. 2011. 起伏地表叠前逆时偏移理论及GPU加速技术. 地球物理学报, 54(7): 1883-1892, doi: 10.3969/j.issn.0001-5733.2011.07.022.

王珺, 杨长春, 冯英杰. 2007. 用优化通量校正传输技术压制数值模拟的频散. 勘探地球物展, 30(4): 252-256.

(本文编辑汪海英)

Acoustic wave equation modeling based on implicit finite difference operators in the time-space domain

CHEN Dong1,2, LIANG Wen-Quan1, XIN Wei1*, YANG Chang-Chun1

1KeyLaboratoryofPetroleumResourcesResearch,InstituteofGeologyandGeophysics,ChineseAcademyofSciences,Beijing100029,China2DongshengJinggongPetroleumDevelopmentCo.Ltd.,ShengliOilfieldCompany,SINOPEC,ShandongDongying257000,China

AbstractNumerical simulation of acoustic wave equation is widely used to synthesize seismograms theoretically, and is also the basis of reverse time migration. With some stability conditions, dispersion often appears when time and the spatial derivatives in the wave equation are gridded. How to suppress such grid dispersion is therefore a key problem for finite difference approaches. Finite-difference formulations of partial differential equations are either explicit or implicit. Implicit formulations can suppress the grid dispersion further and the stability condition is better. Therefore, we propose to satisfy the time-space domain dispersion relationship in a proper range of frequencies. Dispersion analysis and seismic numerical simulation demonstrate the effectiveness of the proposed method.

KeywordsAcoustic wave equation modeling; Time-space domain; Implicit finite difference formulation; Dispersion relationship.

基金项目国家自然科学基金项目(41504142)资助. 国家高技术研究发展计划(2011AA060301)，国家自然科学基金(41204086，41374122)项目联合资助.

作者简介李振春，男，1963年生，教授，博士生导师，主要从事地震波正演及偏移成像方面的研究.E-mail：leonli@upc.edu.cn *通讯作者杨富森，男，硕士研究生.E-mail：sende12345@163.com 陈东，男，1966年生，高级工程师， 2001年于美国科罗拉多矿业学院获石油工程硕士学位，目前在中石化胜利油田东胜公司从事开发研究与管理工作.E-mail：chendong359.slyt@sinopec.com *通讯作者辛维，中国科学院地质与地球物理研究所博士后.E-mail：xinwei@mail.iggcas.ac.cn

doi:10.6038/cjg20160429 中图分类号P631

收稿日期2015-08-27，2016-01-13收修定稿