水平单轴应力与横波反射系数
刘金霞, 崔志文, 王克协
吉林大学物理学院, 长春 130012
水平单轴应力与横波反射系数
刘金霞, 崔志文, 王克协
吉林大学物理学院, 长春130012
摘要地球物理勘探中,地下应力的估测是非常重要的.本文利用应力诱导的弱各向异性的各向异性参数, 借助已有的具有水平对称轴横向各向同性介质顾及高阶小量的横波反射系数近似公式,针对下介质为各向同性受单轴应力作用情况随应力的增加求取应力精度降低的问题,从横波反射系数近似公式的推导出发,联合SH波与SV 波反射系数给出新的改进的单轴应力与横波反射系数的直观表达式;计算并对比了受单轴应力作用的各向同性介质的横波近似和严格的反射系数,并利用理论得到的横波反射系数对应力进行了估值.结果表明,利用改进后横波反射系数与应力的直观表达式, 当应力增加时,应力估值精度有了明显的改善,这为利用横波反射数据直观估测应力提供理论依据.
关键词单轴应力; 弱各向异性; 各向异性参数; 横波反射系数
1引言
地应力在地下是普遍存在的,在地球物理勘探中开展地应力研究具有重要意义.近年来,声弹性理论的发展和应用为地下应力的检测提供了新途径,为从地震数据估测应力提供了新手段.在有限静应力引起的非线性形变上激发小扰动波场是典型的非线性声学中的声弹性问题(Pao et al., 1984),也就是“大加小-small on large”问题.依据声弹性理论,地应力将诱导出介质等效各向异性,Rasolofosaon(1998), Sarkar等(2003)和Prioul等(2004)通过参考构形描述的等效弹性常数把各向异性参数和主应力大小相联系,并通过物理模拟研究验证了这些关系.声弹理论支持直观的预测,一个受三维不等主应力作用的各向同性介质呈现近似的正交各向异性,一个存在单轴应力的各向同性介质呈现近似的横向各向同性.
在地震勘探方法中,人们一直在努力利用纵、横波的振幅资料,以获取更多的介质信息.而地应力引起的静形变不仅仅影响介质中的声速,也会影响波的振幅(Liu et al., 2007;2012),如果能将振幅资料与声弹性理论相结合,从反射幅度直接估测地应力将更有意义.弹性波振幅特征是波传播的基本问题之一,在地球物理勘探和天然地震中均具有重要意义.关于流-固和固-固界面,介质为各向同性或各向异性的弹性波折、反射问题已被广泛研究(Mandal,1991; Ainslie and Burns,1995; Carcione,1997).由于在各向异性介质中纵波和横波反射系数对AVO研究的重要性而被广泛研究 (Rüger,1996,1997,1998).而通常的AVO分析都是以纵波、横波反射系数的解析表达式为基础.既然,受应力作用的介质可以等效为各向异性,就可以利用这些已有的纵波、横波的反射系数公式获取应力信息.Liu等(2009)参考Rasolofosaon等(1998)的工作,采用中间坐标研究了上介质为各向同性,下介质为各向同性受单轴应力作用的纵、横波位移振幅反射系数.此工作的结果表明:(1)可利用横波反射系数估算单轴应力;(2)各向异性参数的正负取值可作为区分单轴应力诱导的还是本征的具有水平对称轴的横向各向同性的(简称HTI地层)一个依据;(3)反射系数随方位的变化可帮助我们初步判断应力的方位.
然而,利用横波反射系数求取应力的结果是随应力的增加准确度降低,特别是当应力较大时(Liu et al., 2009).本文针对随应力的增加准确度降低的问题,在Liu 等(2009)工作的基础上,从横波反射系数近似公式的推导出发分析并改进了单轴应力与横波反射系数的直观表达式,联合SH波和SV波反射系数给出了单轴应力与横波反射系数的直观表达式;将理论得到的横波反射系数,分别代入改进的直观表达式进行应力估值并与已有的结果进行对比,验证了当应力增大时利用改进后的关系得到的应力估值精度有了明显的改善.这一改进的表达式,为利用横波反射数据直观估测应力提供理论依据.
2等效的弹性模量和应力诱导的各向异性参数
我们可以用声弹理论描述应力函数的等效弹性模量矩阵.声弹性理论的前提是在有限静形变(偏置)上叠加小(线性)扰动(Pao et al., 1984).描述介质的位移可以用参考坐标、中间坐标和当前坐标,这三种坐标分别对应介质的三种不同状态,即未变形状态、静形变偏置状态和在该状态上叠加小扰动的形变状态(曹正良等,2003;李刚等,2006).与其对应有三种不同形式的描述介质质点的运动方程.本文选中间坐标及相应的运动方程来描述形变物理量.一般地下岩层所受的应力状态比较复杂,可以分解成均匀静水压力与偏应力的和.均匀静水压力的大小可以等于在某一深度点主应力的平均压力或上覆岩压力.本文将岩层受均匀静水压力时的状态选为参考状态,偏应力与均匀静水压力相比其量值要小得多.中间状态等效的刚度张量Hijkl可表示为
Hijkl=τikδjl+cijkl-cijklwn,n+cijklmnEmn
+cpjklwi,p+cipklwj,p+cijplwk,p+cijkpwl,p.
(1)

(2)
可见方程(2)是具有水平对称轴的等效横向各向同性介质.二阶弹性模量与拉梅系数的关系为c11=λ+2μ, c12=λ和c55=μ,三阶弹性模量c144和c155可分别表示为c144=(c112-c123)/2和c155=(c111-c112)/4.
Rasolofosaon(1998), Sarkar等(2003)和Prioul等(2004)已经开展了应力诱导的各向异性研究,本文仅限于讨论施加于各向同性介质的水平单轴应力,此时应力诱导的弱各向异性参数可表示为
(3)

3改进的应力与横波反射系数关系公式
已有的本征HTI介质顾及高阶小量的(Rüger,1996)横波反射系数近似公式为


(4)
由方程(4)入射平面与对称平面成0°和90°的横波反射系数分别做差可得
(5)

(6)
方程(5)与Liu等(2009)得到的方程是一样的,而方程(6)与Liu等(2009)的工作相比较多了最后顾及的高阶项.由方程(5)和方程(3)可得到Liu等(2009)的与SH波有关的方程:
(7)
由方程(6)忽略第三项依据方程(3)可得Liu等(2009)的与SV波有关的方程:
(8)
(9)
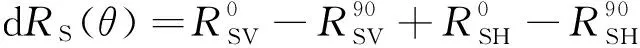
4计算考察
这部分计算模型的上介质为各向同性,下介质是各向同性受单轴应力作用.计算参数见表1,上介质是各向同性的Castlegate砂岩,下介质分别是参数1和2(Liu et al.,2009).本文的单轴应力为压缩应力,用负号代表压缩应力.我们计算对比了横波近似和严格的反射系数.并利用改进后的横波反射系数与应力的直观表达式,估测应力,并与Liu等(2009)给出的直观公式结果作对比.严格的反射系数的计算主要基于在岩石中存在塑性形变的声波折反射系数的计算(见Liu et al.(2007)公式(15),或刘金霞(2007)公式(3.8)).当应力没有引起塑性形变时,即可退化为本文弹性静形变情况.对比了已有文献的结果(Yardley et al.,1991),数值结果和文献的结果是一致的,证实了我们计算结果的可信度.

表1 地层参数
图1和图2给出了从各向同性介质入射到受单轴应力作用(沿X1)的介质,入射平面和对称平面成0°和90°的SH和SV波的反射系数.实线是严格的理论结果;虚线是由近似公式(4)计算的结果.在近似的横波反射系数与理论计算的严格结果的对比中可以看到,在小的入射角,小的单轴应力例如-3 MPa理论值和横波的近似值基本一致,但随着应力的增加在方位90° 的SH波和方位0°的SV波甚至在较小的入射角偏差明显变大.而Rüger(1996)等给出的横波近似公式,恰对方位0° 的SV波和方位90° 的SH波近似公式进行了进一步的近似处理.这一明显的偏差与Rüger(1996)等的进一步近似处理有直接关系.

图1 入射平面和对称平面成0°和90°的SH波的反射系数(a)和(b)下介质参数为Berea A,应力分别是-3和-10 MPa; (c)和(d)下介质参数为Berea B,应力分别是-3和-10 MPa; 实线是严格的理论结果,虚线是由近似公式计算的结果.Fig.1 SH-wave reflection coefficients at an interface between an isotropic medium and an anisotropic medium induced by uniaxial horizontal stressSolid line denotes the exact solution and dashed line denotes weak anisotropic approximation for azmuthal angles 0° and 90°. (a) -3 MPa for Berea A; (b) -10 MPa for Berea A; (c) -3 MPa for Berea B; (d) -10 MPa for Berea B.
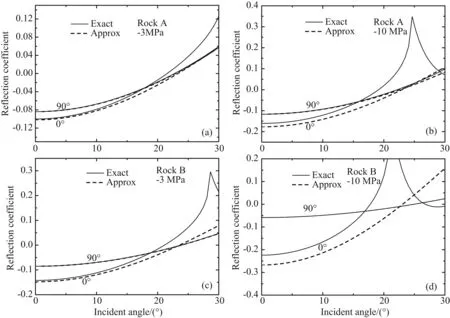
图2 入射平面和对称平面成0°和90°的SV波的反射系数(a)和(b)下介质参数为Berea A,应力分别是-3和-10 MPa; (c)和(d)下介质参数为Berea B,应力分别是-3和-10 MPa; 实线是严格的理论结果,虚线是由近似公式计算的结果.Fig.2 SV-wave reflection coefficients at an interface between an isotropic medium and an anisotropic medium induced by uniaxial horizontal stressSolid line denotes the exact solution and dashed line denotes weak anisotropic approximation for azmuthal angles 0° and 90°. (a) -3 MPa for Berea A; (b) -10 MPa for Berea A; (c) -3 MPa for Berea B; (d) -10 MPa for Berea B
图3是由理论计算求得严格的SH波反射系数,再代入改进前的近似公式(7)式求应力值.由图3a,在入射角小于10°的范围,所求应力几乎与入射角度无关,求得的应力值分别约为-2.68 MPa、-4.20、-6.16、-7.30 MPa和-8.32 MPa.相对误差分别约为10.7%、16.0%、23.0%,27.0%和30.7%. 由图3b,在入射角小于10°的范围,分别求得的应力值约为-2.74、-4.36、-6.56、-7.92 MPa和-9.20 MPa,其相对误差分别约为8.7%、12.8%、18.0%、20.8%和23.3%.可以看到随着应力的增加由改进前的(7)式求应力值的准确度开始降低.分析其原因有两方面:一、随应力的增加各向异性明显变大,导致偏离的增加;二、由于Rüger(1996)等的进一步近似,随应力增加反射系数近似结果偏离增加,导致估测精度降低.
图4是由理论计算求得严格的SV波反射系数,再代入改进前的近似公式(8)式求应力.由图4a,在入射角小于10°的范围,所求应力值分别约为-2.68~-2.44 MPa、-4.20~-3.75 MPa、-6.16~-5.34 MPa、-7.29~-6.18 MPa和-8.31~-6.89 MPa.相对误差分别约为10.7%~18.7%、16.0%~25.0%、23.0%~33.3%、27.1%~38.2%、30.8%~42.5%.由图4b,在入射角小于10°的范围,所求应力值分别约为-2.74~-2.57 MPa、-4.36~-4.05 MPa、-6.56~-6.00 MPa、-7.91~-7.16 MPa和-9.20~-8.23 MPa.相对误差分别约为8.7%~14.3%、12.8%~19.0%、18.0%~25.0%、20.9%~28.4%、23.4%~31.4%.可以看到随着应力的增加由改进前的 (8)式求应力值的准确度也开始降低.
图5是由理论计算求得严格的横波反射系数,再代入本文改进后的公式(9)式求应力,由图5a可以看出,在入射角小于10°的范围,所求应力值分别约为-3.65~-3.53 MPa 、-6.02~-5.76 MPa,

图3 由改进前的与SH波有关的公式 (7)求应力(a) 下介质为参数Berea A,实际的应力分别是-3,-5,-8,-10和-12 MPa; (b) 下介质为参数Berea B,实际的应力分别是-3,-5,-8,-10和-12 MPa.Fig.3 The stress inverted by the relationship between SH-wave reflection coefficients and uniaxial stress.(a) Lower rock is Berea A; (b) Lower rock is Berea B.
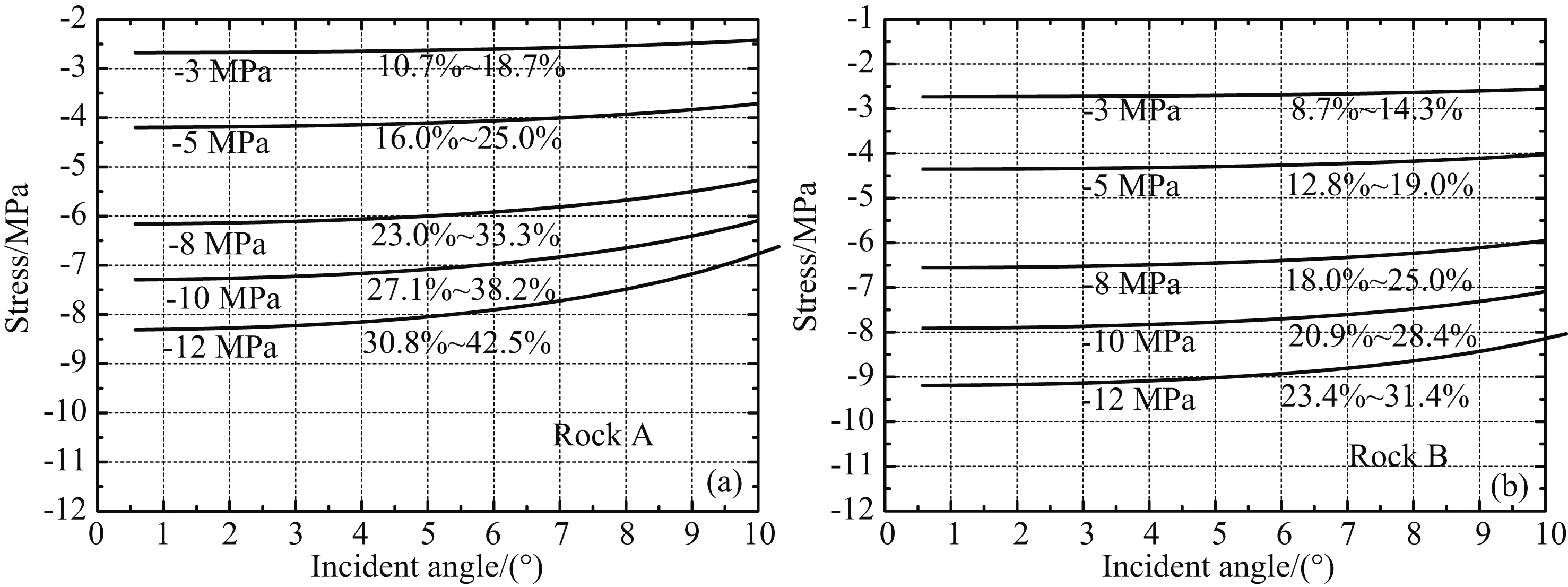
图4 由改进前的与SV波有关的公式(8)求应力(a) 下介质为参数Berea A,实际的应力分别是-3,-5,-8,-10和-12 MPa; (b) 下介质为参数Berea B,实际的应力分别是-3,-5,-8,-10和-12 MPa.Fig.4 The stress inverted by the relationship between SV-wave reflection coefficients and uniaxial stress.(a) Lower rock is Berea A; (b) Lower rock is Berea B.
-9.51~-8.94 MPa、-11.83~-11.00 MPa和-14.13~-12.93 MPa.相对误差分别约为 17.7%~21.7%、15.2%~20.4%、11.8%~18.8%、10.0%~18.3%和7.8%~17.8%.由图5b,在入射角小于10°的范围,所求应力值分别约为-3.42~-3.33 MPa、-5.64~-5.43 MPa, -8.91~-8.45 MPa、-11.08~-10.40 MPa和-13.24~-12.30 MPa.相对误差分别约为11.0%~14.0%,8.6%~12.8%,5.6%~11.4%,4.0%~10.8%和2.4%~10.4%.对比可见对压缩应力大于5 MPa,由改进后的横波公式求得的应力精度明显提高,仍以-10 MPa为例,其误差在4.0%~18.3%.而对压缩应力小于5 MPa,其误精度没有改善.究其原因是,应力较小时,两个方位横波反射系数的差别比较小,而近似和严格的横波反射系数结果基本一致,而这种横波反射系数的差再相加可能又扩大了其他的近似处理所引起的误差.
图6给出了方程(9)的分子和分母随入射角的变化.点划线代表与横波有关的分子,虚线是与横波有关的的分母,实线是他们的比值.图示结果表明方程(9)的分母随角度快速增加,而分子随角度缓慢增加,因此其比值除了在较小的角度外也会比较稳定(见实线).由实线可见在1°~10°的范围都是稳定的,因此是可应用的.

图5 由改进后的横波有关的公式 (9)求应力(a)下介质为参数Berea A,实际的应力分别是-3,-5,-8,-10和-12 MPa; (b)下介质为参数Berea B,实际的应力分别是-3,-5,-8,-10和-12 MPa.Fig.5 The stress inverted by the relationship between shear-wave reflection coefficients and uniaxial stress.(a) Lower rock is Berea A; (b) Lower rock is Berea B.

图6 方程(9)分子分母随角度的变化虚线代表方程的分母,点划线代表方程的分子,实线是分子和分母的比值.Fig.6 The numerator and denominator of the formulation(9) as a function of the incident angleDash dot line,dash line and thick line denote the numerator,denominator of formulation, and the ratios of numerator to denominator dRS(θ)/DRS(θ) respectively.
5结论
本文利用应力诱导的弱各向异性的各向异性参数, 借助已有的本征HTI介质顾及高阶小量的横波反射系数近似公式,针对下介质为各向同性受单轴应力作用情况随应力的增加求取应力精度降低的问题,对相对大些的单轴应力情况,发现通过将在入射平面与HTI介质对称轴成0°和90°的横波反射系数差相加的方法,可以消除由于在推导横波近似公式采用的一些近似所带来的误差.联合SH波与SV波反射系数给出了改进的单轴应力与横波反射系数的直观表达式;计算并对比了受单轴应力作用的各向同性介质的横波近似和严格的反射系数,并利用理论得到的横波反射系数对应力进行了估值.以-10 MPa的单轴应力为例,在入射角小于10° 的范围内,改进前的结果其估测的相对误差在20.8%~38.2%,利用改进后横波反射系数与应力的直观表达式其估测的相对误差在4.0%~18.3%,应力估值精度有了明显的改善.这一改进的表达式,为相对大些的单轴应力情况(例如本文当单轴应力大于5 MPa),利用横波反射数据估测应力提供理论依据.因此,我们可以用已有的应力与横波的直观公式(Liu et al.,2009),利用横波反射数据对应力进行估测和预判,再利用本文改进的公式进行修正,这对实现用横波反射数据估测单轴应力具有指导意义.
References
Ainslie M A, Burns P W. 1995. Energy-conserving reflection and transmission coefficients for a solid-solid boundary.J.Acoust.Soc.Am., 98(5): 2836-2840.
Cao Z L, Wang K X, Li G, et al. 2003. Dipole flexural waves splitting induced by borehole pressurization and formation stress concentration.ChineseJ.Geophys. (in Chinese), 46(5): 712-718.
Carcione J M. 1997. Reflection and transmission of qP-qS plane waves at a plane boundary between viscoelastic transversely isotropic media.Geophys.J.Int., 129(3): 669-680.
Johnson P A, Rasolofosaon P N J. 1996. Nonlinear elasticity and stress-induced anisotropy in rock.J.Geophys.Res., 101(B2): 3113-3124.
Li G, Wang K X, Liu J X, et al. 2006. Acoustoelasticity theory, numerical analysis and practical example of the cased hole with stress concentration by cross-dipole acoustic logging.ChineseJ.Geophys. (in Chinese), 49(1): 295-304.
Liu J X. 2007. Acoustoelastic effects on reflection and transmission of elastic waves and guided waves in a borehole surrounded by a transversely isotropic (VTI) elastic solid[Ph. D.](in Chinese). Changchun: Jilin University.
Liu J X, Cui Z W, Wang K X. 2007. Reflection and transmission of acoustic waves at the interface between rocks in the presence of elastic-plastic deformations.J.Geophys.Eng., 4(2): 232-241. Liu J X, Cui Z W, Wang K X. 2009. The relationships between uniaxial stress and reflection coefficients.Geophys.J.Int.,179(3): 1584-1592.
Liu J X, Cui Z W, Wang K X. 2012. Effect of stress on reflection and refraction of plane wave at the interface between fluid and stressed rock.SoilDynamicsandEarthquakeEngineering, 42: 47-55.
Mandal B. 1991. Reflection and transmission properties of elastic waves on a plane interface for general anisotropic media.J.Acoust.Soc.Am., 90(2): 1106-1118.
Pao Y H, Sachse W, Fukuoka H. 1984. Acoustoelasticity and ultrasonic measurements of residual stresses.∥ Mason W P, Thurston R N eds. Physics Acoustics. New York: Academic Press, 17: 61-143.
Prioul R, Bakulin A, Bakulin V. 2004. Nonlinear rock physics model for estimation of 3D subsurface stress in anisotropic formations: Theory and laboratory verification.Geophysics, 69(2): 415-425.
Rasolofosaon P. 1998. Stress-induced seismic anisotropy revisited.RevueDel′InstitutFrancaisduPetrole, 53(5): 679-692.
Rüger A. 1996. Analytic insight into shear-wave AVO for fractured reservoirs. ∥ SEG Technical Program Expanded Abstracts. 1801-1804.
Rüger A. 1997. P-wave reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry.Geophysics, 62(3): 713-722.
Rüger A. 1998. Variation of P-wave reflectivity with offset and azimuth in anisotropic media.Geophysics, 63(3): 935-947.
Sarkar D, Bakulin A, Kranz R. 2003. Anisotropic inversion of seismic data for stressed media: Theory and a physical modeling study on Berea Sandstone.Geophysics, 68(2): 690-704.
Tsvankin I. 1997. Reflection moveout and parameter estimation for horizontal transverse isotropy.Geophysics, 62(2): 614-629.
Yardley G S, Graham G, Crampin S. 1991. Viability of shear-wave amplitude versus offset studies in anisotropic media.Geophys.J.Int., 107(3): 493-503.
附中文参考文献
曹正良, 王克协, 李刚等. 2003. 井孔压力与地层应力集中诱导的偶极弯曲波的分裂. 地球物理学报, 46(5): 712-718.
李刚, 王克协, 刘金霞等. 2006. 套管井应力集中下正交偶极声测井的声弹理论、数值分析与实例. 地球物理学报, 49(1): 295-304. 刘金霞. 2007. 弹性波折、反射与横向各向同性(VTI)介质井孔导波声弹效应研究[博士论文]. 长春: 吉林大学.
(本文编辑汪海英)
Relationships between uniaxial stress and S-wave reflection coefficients
LIU Jin-Xia, CUI Zhi-Wen, WANG Ke-Xie
CollegeofPhysics,JilinUniversity,Changchun130012,China
AbstractThe investigation of subsurface stress is most important for geophysical exploration. This paper analyzed relationships between uniaxial stress and S-wave reflection coefficients based on the known weak-anisotropy approximations for the anisotropic parameters in stressed media and the reflection coefficients in anisotropic media. We proposed a new simple relationship to improve the estimation accuracy of larger uniaxial stress for an interface between an isotropic overburden and an anisotropic medium induced by horizontal uniaxial stress. The approximate S-wave reflection coefficients are compared with the exact ones in stressed media by numerical calculations, and the improved direct relationships between uniaxial stress and S-wave reflection coefficients are used to estimate the magnitude of stress. The results show the simple formulations given in this paper are stable and useful except degree is close to zero, and the error of uniaxial stress estimated from S-wave become smaller than before when uniaxial stress is more than 5 MPa. Therefore, the improved direct relationships between uniaxial stress and S-wave reflection coefficients will be helpful to estimate the magnitude of stress.
KeywordsUniaxial stress; Weak-anisotropy; Anisotropic parameters; S-wave reflection coefficients
基金项目国家自然科学基金项目(41474098,41004044,11134011)资助.
作者简介刘金霞,女,1977年生,博士,主要从事声弹性、声波测井理论与应用方法研究. E-mail:jinxiajlu@163.com; cuizw@jlu.edu.cn
doi:10.6038/cjg20160427 中图分类号P631
收稿日期2014-12-02,2016-01-13收修定稿
刘金霞, 崔志文, 王克协. 2016. 水平单轴应力与横波反射系数.地球物理学报,59(4):1469-1476,doi:10.6038/cjg20160427.
Liu J X, Cui Z W, Wang K X. 2016. Relationships between uniaxial stress and S-wave reflection coefficients.ChineseJ.Geophys. (in Chinese),59(4):1469-1476,doi:10.6038/cjg20160427.

