生活中的一次函数
马娇
生活中的一次函数
马娇
数学来源于生活,又服务于生活,同学们若能灵活运用数学知识解决生活问题,不仅能提高对数学知识的掌握理解能力,更能提高对知识的综合运用水平.
函数是初中数学的重要内容,在生活中,一次函数随处可见:某人带了100元钱,要去买3元一只的羽毛球,他买了x只羽毛球,剩下的钱数y=-3x+100,在这里-3是一次函数中k的值,它的实际意义是买一个羽毛球花了3元,100是一次函数中b的值,它的实际意义是该人共带了100元.本文通过几例生活中常见问题的分析,提供函数问题的处理方法,希望能帮助同学们更好地解决实际问题.
例(2010·江苏无锡)某客船往返于A、B两码头,在A、B间有旅游码头C.客船往返过程中,船在C、B处停留时间忽略不计,设客船离开码头A的距离s(千米)与航行的时间t(小时)之间的函数关系如图1所示.根据图像提供的信息,解答下列问题:

图1
(1)船只从码头A→B,航行的速度为______千米/时;船只从码头B→A,航行的速度为______千米/时;
(2)过点C作CH∥t轴,分别交AD、DF于点G、H,设AC=x,GH=y,求出y与x之间的函数关系式;
(3)若旅游码头C设在离A码头30千米处,一旅游团队在旅游码头C分两组行动,一组乘橡皮艇漂流而下,另一组乘船到达码头B后,立即返回.
①求船只往返C、B两处所用的时间;
②两组在途中相遇,求相遇时船只离旅游码头C有多远.
【分析】根据本题提供的背景,不难看出是行程问题中的水流问题,同学们若能快速结合图像中D(3,90)、F(7.5,0)的实际意义,便能顺利求出顺流的速度VA→B== 30(km/h),逆流的速度VB→A==20(km/ h),进而求出静水中的速度25 km/h和水流速度5 km/h.
在大家解答问题(2)的过程中发现,有三种不同的解决策略,供大家交流.
方法1:函数解析法
【思路分析】利用题目给定的函数信息,将AC=x转化成函数意义为客船从A驶向B离开A码头x km,客船从B返回A还距离A码头x km,GH表示客船在往返A、B两码头的过程中离A码头还有x km要用的时间,因而GH表示两个时间的差,只需求出表示AD、DF两条直线的解析式,当s=x后H与G两点横坐标的差即为y与x的函数关系式.
【解析】由题知:sAD=30t,sDF=-20t+150;
当s=x时,tG=,tH=;
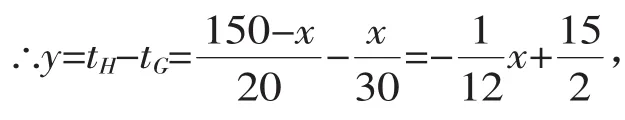
温馨提示:函数图像的呈现使我们可以直接利用图像信息(图像上有具体数值的点坐标)求出函数解析式,根据函数解析式结合问题中的量的含义进行函数信息的转化.利用函数解析式解决实际问题关键在于找到并理解图像信息中的点的实际意义,正确与实际问题中的相关量进行转化,利用函数解析式进行解答.这一方法培养了同学们的函数思想,在理解函数信息的基础上巧妙与实际问题联系,提升同学们的函数识图能力,提高同学们解决函数问题的能力.
方法2:实际应用法
【思路分析】将本问题实际化,CH∥t轴,说明GH表示的是时间,将GH转化成客船从离A码头x km的地方出发到B码头后返回到刚才的出发地所用的时间,而AB间的距离为90 km,出发地离A码头x km,故往返所行进的距离为90-x,利用时间的计算公式求出两端的时间和就可.
【解析】由(1)已知顺流的速度VA→B==30(km/h),逆流的速度VB→A==20(km/h);

【温馨提示】函数问题的背景是实际生活情境,将函数问题实际化,利用实际问题的处理思路和方法,抓住实际生活问题中的公式,用实际生活背景方式解决.同学们对于行程问题很是熟悉,根据水流问题中的顺流、逆流公式及行程问题中的线段分析方法,同学们能较快正确地利用速度、时间与路程之间的关系表示出题中线段的含义,进行解决.这一方法培养了同学们实际问题的处理能力,提升了大家的互化技能,突出了函数信息实际问题解决策略的运用.
方法3:几何图形法
【思路分析】不受题目给定的函数图像诱导,把题目条件看作为几何图形,由CH∥t得到三角形相似,利用相似三角形的性质得出比例列出关系式.
【解析】设CH交DE于P,则PE=AC= x,DP=90-x,∵CH∥t,∴△DGH∽△DAF,

【温馨提示】将函数信息问题几何图形化,把函数图像抽象成几何图形,抓住几何图形的性质得到关系式列出等式得出结论.函数图像几何图形化是解决函数信息题的一种好方法,由于在函数图像中会出现一些与坐标轴平行的线段,因而利用线段的关系可以转化成几何图形中的全等、相似或直角三角形等相关知识加以解决.这一方法培养了大家的识图能力,提升学生的图形间互化的技能.
对于问题(3),同学们理解了问题(2)的三种不同的处理方法,运用实际应用法或函数图像解析法就可解决,本文介绍函数解析法供参阅.
如图建立坐标系,设客船、橡皮艇离开码头C的距离s(千米)与航行的时间t(小时)之间的函数关系如图2所示.

图2
SAB=-20t+100,SOC=5t,
由题知-20t+100=5t,t=4,
故S=5×4=20.
从上述两例可以看出一次函数所描述的关系在生活中很多,利用一次函数可以更好地认识生活中一些事物的规律.笔者在进行生活数学问题的教学中发现很多同学在处理过程中只会解题,不会思考,不会类比,不会抓问题的关键,更不会主动提问,处理问题和灵活应变的能力都很薄弱.因而希望同学们在解答数学问题时要抓住问题的症结,充分挖掘题目中的信息与数学知识的联系,巧妙利用数学知识对实际生活中的问题进行转化,构建数学模型进行有效解答,提升自己的综合实力.
(作者单位:江苏省无锡市阳山中学)


