认清坐标 突破难点

何林峰



认清坐标突破难点

何林峰

同学们，在学习了《平面直角坐标系》这一章后，相信你们既有对坐标平面（即二维空间）的好奇，也有很多的困惑和不解.现将本章的重难点进行勾画并和大家共同探讨突破的最佳方法.

一、熟悉各象限及坐标轴上点的坐标特征

例1已知点P（x-1，2x-5）在第四象限，且x为整数，求x.

【分析】解决本题的关键在于，既要对各象限点的坐标的符号特征清楚，还要能由点的坐标特征建立关于x的不等式（组）求其整数解.

解这个不等式得1＜x＜2.5，

又∵x为整数，∴x=2.

二、理解对称点之间的坐标特点

例2已知点A（x-2，-1），点B（y+3，x+y）关于x轴对称，求x和y.

【分析】关于x轴对称的两个点必须满足：它们的横坐标相等，纵坐标互为相反数.据此建立关于x、y的方程组解决问题.

【解析】∵A、B两点关于x轴对称，

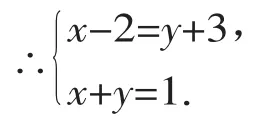
解这个方程组得x=3，y=-2.

三、掌握坐标与长度间的转化

例3如图A（0，2），B（1，0），以AB为边在第一象限作正方形ABCD，求C，D两点的坐标.

【分析】欲求C点坐标，则会联想到过C点作x轴的垂线（CE），就是要求CE和OE的长，进而就是要求CE和OB以及BE的长，考虑到A（0，2），B（1，0），进而会联想CE、BE与OA、OB是否有关系，从而想到利用△BEC≌△AOB求解.同理可求D点坐标，这里就体现了坐标——长度——坐标的转化思想.

【解析】过C点作CE⊥x轴于E，过D点作DF⊥y轴于F，由△DFA≌△BEC≌△AOB可得AF=BO=CE=1，DF=AO=BE=2，从而C（3，1），D（2，3）.

（作者单位：江苏省泰州中学附属初级中学）