基于OpenFOAM的桥梁主梁断面静气动性能研究*

应旭永　ZASSO Alberto　许福友

(大连理工大学桥梁工程研究所1)　大连　116023 )

基于OpenFOAM的桥梁主梁断面静气动性能研究*

应旭永1)ZASSO Alberto2)许福友1)

(大连理工大学桥梁工程研究所1)大连116023 )

摘要：以意大利某斜拉桥为工程背景，通过风洞实验和CFD数值模拟对闭口箱型主梁断面的静气动性能进行了研究.基于开源程序OpenFOAM，数值模拟了方形断面和不同攻角下主梁断面的静气动系数和表面压力系数分布，将模拟得到的结果与实验结果进行了对比分析，进一步研究了主梁断面下表面圆倒角对静气动性能的影响，并从流场的角度定性的对计算实验结果进行了机理解释.结果表明：OpenFOAM模拟得到的方形断面和不同攻角下主梁断面气动系数和实验结果基本吻合；对于闭口箱型主梁断面，下表面圆倒角对其气动性能有较大的改善作用.

关键词：数值模拟;OpenFOAM;主梁断面;气动性能;三分力系数

0引言

现代桥梁跨径日益增大，使得结构的阻尼和刚度大幅度降低，导致结构对风的作用更加敏感，因此桥梁结构的风振稳定性成为大跨度桥梁安全的控制因素之一.长期以来，风洞实验是桥梁气动性能研究的最直接手段[1].郭震山[2]通过缩尺节段模型实验，测量了一桥梁主梁断面不同攻角下的静气动三分力系数，并进一步研究了其邻近新建桥梁对既有桥梁的气动干扰效应.周立等[3]通过风洞实验研究了栏杆、汽车等对汽车-主梁桥面系统的静气动性能的影响.

Vairo[4]采用有限体积法模拟了典型桥梁断面的三分力系数；Sarwar等[5]基于大型商用计算流体力学(CFD)求解器Fluent，采用三维大涡模拟技术模拟了一典型流线型主梁断面的绕流场，同时研究了附属设施对主梁断面静气动性能的影响；应旭永等[6]基于Fluent求解器模拟了苏通大桥主梁断面的绕流场，并提出一种基于连续扭转振动的三分力系数快速数值识别方法，显著提高了计算效率.此外，国内许多学者对桥梁断面静气动性能也进行过许多数值模拟研究[7-8].相比风洞实验，基于CFD的数值模拟方法具有低成本、省人力、快捷等优点，并具有很好的可重复性，而且方便设置不同的参数以及考察它们的影响，便于工程结构初始选型和优化设计.

OpenFOAM是基于C++编写的开源CFD程序，其开放性、完全面对对象的程序设计和完善的分层框架构件，方便用户开发新的模型和求解器.本文以意大利某斜拉桥为工程背景，通过节段模型测力风洞实验，识别出该桥主梁断面不同攻角下的静气动三分力系数和表面压力系数分布，同时基于OpenFOAM建立了方形断面和该桥主梁断面绕流场模拟的数值模型，并将模拟得到的结果与实验结果进行了对比分析.进一步研究了主梁断面下表面倒角对静气动性能的影响，并从流场的角度定性的对实验结果和计算结果进行了机理解释.

1风洞实验测试

对图2所示主梁断面进行了节段模型风洞实验，该断面是意大利某已建成斜拉桥的主梁断面，实验在米兰理工大学风洞实验室中进行，主梁节段模型宽1 m，长2.91 m，见图1～2.节段模型除气动外形相似以外还需要要求刚度足够大，模型骨架由铝合金杆件构成，模型的风嘴段和中间段分别采用木板和铝合金薄板来模拟外衣以保证几何相似性.需要指出的是，实际桥梁主梁断面底板与斜腹板的夹角是尖角，而实验模型由于此处采用铝合金薄板来模拟外衣，很难做到尖角，所以对于实验模型相当于在底板与斜腹板的夹角处倒了一个很小尺寸的圆角.本文后续数值模拟将会探讨此处倒角对断面静气动性能的影响.

图1　模型断面图(尺寸单位：m)

图2　主梁节段模型实验装置

测力系统安装在节段模型的中心，为了提高测力系统的精度，本实验采用两端设置补偿段来减小模型端部的三维效应.测压系统由绕着模型中心位置的78个测压点组成，并分别连接高频压力扫描阀，采样频率为100 Hz.

2数值计算方法

2.1流体控制方程

结构风工程中的流体为近地层大气，可看做是近似不可压牛顿粘性流体.在直角坐标系下，连续性方程和不可压N-S方程(动量方程)为

(1)

(2)

式中:i,j为1,2；空气密度ρ为1.225 kg·m-3;粘性系数ν为1.46×10-5Pa·s.为考虑湍流效应，引入SST 湍流模型，该模型能够能够广泛适用于各种复杂流动.SST 模型具体形式以及参数取值可参考文献[9]，本文不再赘述.

OpenFOAM采用有限体积法离散求解Navier-Stokes方程组，本文将基于OpenFOAM程序中的非定常湍流求解器pisoFoam进行求解.计算过程中采用限制线性格式离散N-S方程组对流项，用欧拉隐式格式进行时间推进，速度压力耦合采用压力的隐式算子分割算法(PISO)进行求解.

2.2几何建模与网格划分

方柱绕流是流体力学领域非常经典一种绕流问题，在桥梁结构中，拱肋、桥塔塔柱、墩台等计算也经常设计成方形截面.为了验证本文数值模拟方法的精度，首先利用OpenFOAM模拟了方柱的非定常绕流场.国内外很多学者通过风洞实验或是数值模拟对方柱绕流进行了深入研究，也为本文的验证计算提供了重要的对比依据.

主梁断面尺寸见图1，缩尺比为1∶30.整个计算域包含结构化网格和非结构化网格，内层为结构化网格，外层为非结构化网格，桥梁断面的近壁面网格见图3.计算域进口处采用速度进口边界条件；出口处为完全发展出口边界；断面表面采用无滑移壁面，近壁处用增强壁面函数法来处理；计算域两侧采用自由边界条件.

图3　主梁断面近壁面区网格划分

3计算结果分析

3.1静气动参数

静气动三分力系数是桥梁静气动特性研究的一项基本内容.按体轴坐标系桥梁断面上的三分力系数为

(3)

式中：ρ，U分别为空气密度和来流平均风速；B，D分别为桥梁断面宽度和高度；FH，FV，MT为相应的桥梁断面单位长度上受到的气动阻力、升力和扭矩；CD，CL，CM分别为阻力系数、升力系数和扭矩系数.

Strouhal数是反应漩涡脱落频率相对来流速度快慢的量纲一的量，表达为

(4)

式中：f为漩涡脱落频率，可以由升力系数时程曲线通过频谱分析得到，也叫Strouhal频率；U为自由来流风速.

3.2方柱计算结果

表1给出了本文数值模拟计算的雷诺数Re=21 400方柱静气动参数与文献结果的对比.可见，本文通过OpenFOAM模拟得到的方柱平均阻力系数、脉动升力系数和Strouhal数与实验结果吻合的很好，而且与文献[10]采用FLUENT软件的计算结果也基本一致.图4给出了方柱表面平均压力系数的数值模拟结果与实验结果的比较.可以注意到2个实验结果存在一些差异，尤其在上、下表面和后表面，说明钝体绕流问题本身对周围流场参数是非常敏感的；本文数值模拟得到的压力系数结果基本处在2个实验结果中间.以上结果表明，本文数值方法方法可以较为准确的模拟钝体断面的非定常绕流场.

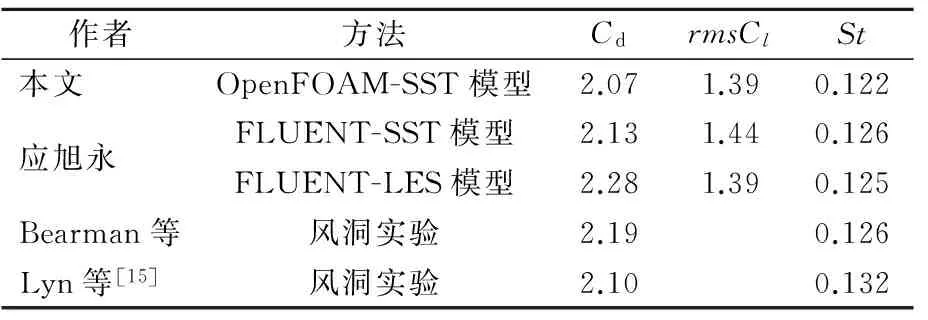
表1　方柱绕流OpenFOAM计算结果与文献结果的比较

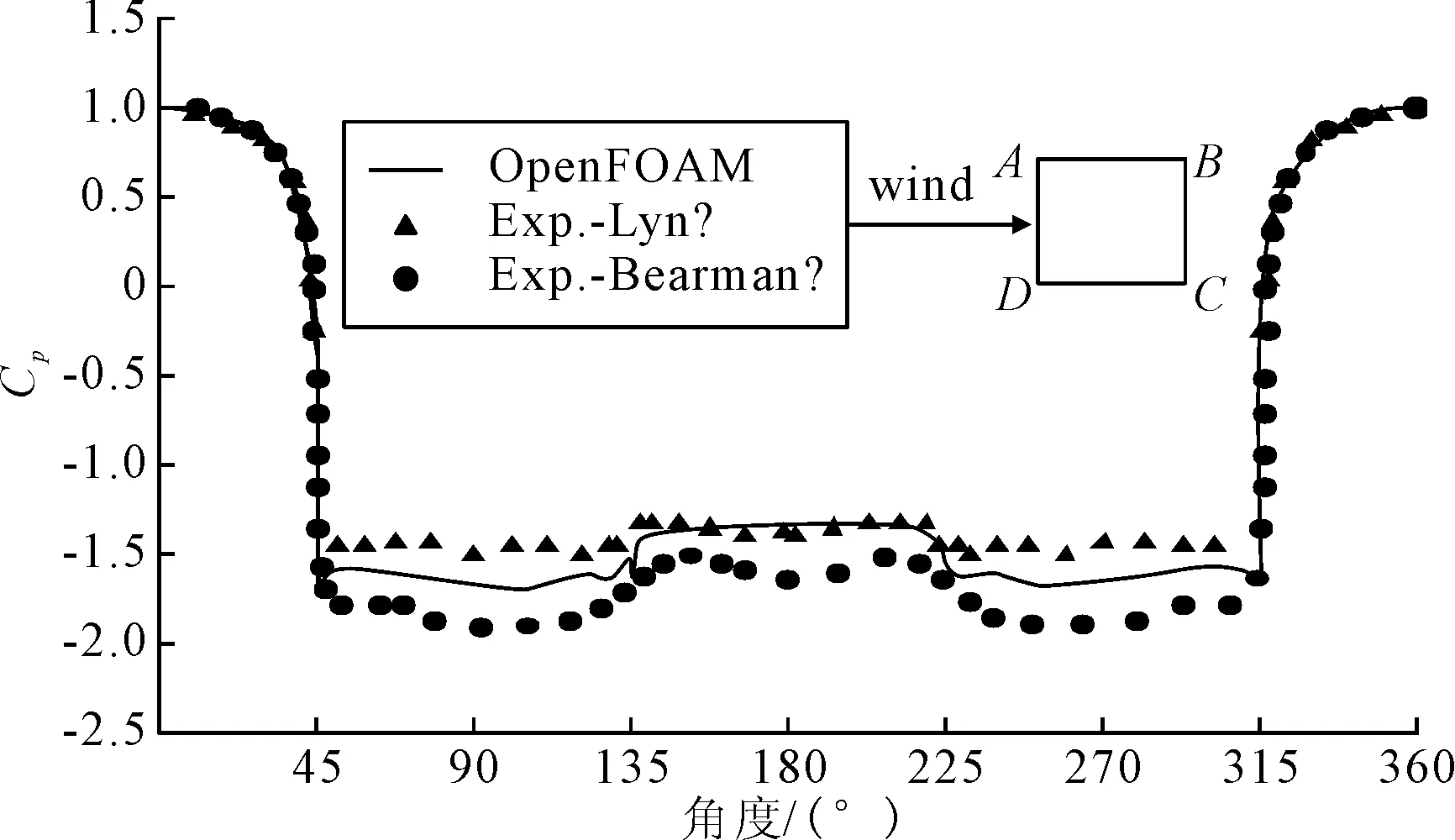
图4　方柱表面平均压力系数分布

4主梁断面计算结果分析

利用相同的数值模拟方法，同时为了考察下表面倒角对模型静气动性能的影响，分别数值模拟了桥梁断面原始模型(R/B=0)和两种不同尺寸倒角模型(R/B=0.05，R/B=0.1)的绕流场.图5给出了不同攻角下三分力系数的实验结果和数模模拟结果的对比.可见在较小攻角范围内，阻力系数的变化幅度较小，但是随着攻角的进一步增大，由于模型断面迎风面积的迅速增大，使得阻力系数急剧增大.由于断面上、下表面不对称，造成了阻力系数在正、负攻角下的变化斜率有些差异.在负攻角下，测压实验得到的阻力系数要比测力实验得到的阻力系数要偏小，这种偏差主要是由于测力实验考虑了模型表面粗糙度对气动力的影响，而测压实验和数值模拟均未考虑这种影响.此外，0°攻角和-6°攻角下，数值模拟的阻力系数计算结果和测压实验结果基本吻合，此时模型下表面倒角对阻力系数的影响也不大；6°攻角下，原始模型的数值模拟结果要比实验结果偏大50%左右，但是下表面倒圆角模型的阻力系数与实验结果基本吻合.

图5　三分力系数实验结果和数模模拟结果的对比

随着攻角的增大，模型的升力系数和扭矩系数单调增大.当攻角大于6°时，升力系数的增大幅度逐渐放缓，而扭矩系数随着攻角的增大而减小.升力系数和扭矩系数的数值模拟值结果变化趋势能与实验结果保持一致.6°攻角下，下表面倒角使断面升力系数大幅度减小，其余攻角影响不大.此外，下表面倒角对各攻角下的扭矩系数影响均较小.

图6给出了不同攻角下，原始断面和倒角断面模拟得到的时均流线图对比.可见0°攻角下，流线在模型上表面迎风端发生了较小的分离，很快又再附到模型表面，并在上表面后缘再次发生分离；流线在模型下表面迎风端未发生分离，沿着模型表面在底板后缘和斜腹板的夹角处发生分离；尾流区由于流线的分离生成了一对较大的反向回流涡.对比原始断面和倒角断面的流线图，两者的流场特性在0°攻角下基本一致，因此此时两种模型的三分力系数也基本相同.

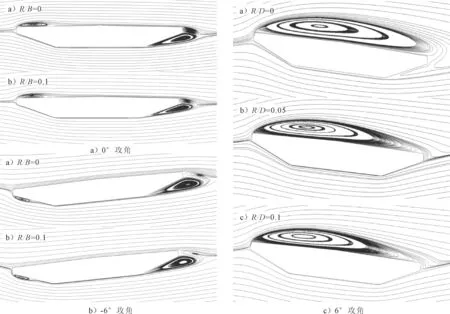
图6　不同攻角下原始断面和倒角断面的时均流线图对比

-6°攻角下，流线在模型上表面迎风端未发生分离，而在上表面后缘才发生分离；在下表面迎风端，流线发生了较小的分离，并生成了一个较小的分离涡，流线很快又再附到斜腹板表面，直到底板后缘和斜腹板的夹角处发生再次分离.此外，-6°攻角下，模型下表面倒角对绕流场特性也几乎没有影响.

6°攻角下，原始模型和倒角模型的流线图产生了较大的差异.随着攻角的增大，模型上表面流动的分离大幅度的增强，对于原始断面，分离后的流线并未在上表面发生再附，而对于倒角断面，分离后的流线在上表面后缘发生了再附.模型下表面倒角削弱了流动的分离强度，分离剪切层也更加靠近模型表面，从而导致此时倒角断面的阻力系数要相对较小.流动在模型下表面迎风端均未发生分离，但在底板后缘和斜腹板的夹角处，原始断面发生了再次分离，而倒角断面未发生分离.图7给出了6°攻角下原始模型和倒角模型的表面时均压力系数分布对比，可见下表面倒角减小了上表面的压力值、增大了下表面的压力值，从而导致此时倒角断面的升力系数要相对较小.倒角断面的压力系数分布与实验结果更加的吻合，尤其是下表面的分布.此外，不同尺寸的倒角对断面绕流场及压力系数分布影响不大.

图7　6°攻角下原始模型和倒角模型的表面时均压力系数分布

由以上数值模拟结果可见，断面外形的细微变化会对其气动性能产生较大的影响.对于类似本文研究的闭口箱型主梁断面，在正攻角下，下表面倒角会一定程度上抑制断面流动分离，大幅度的减小断面三分力系数，从而改善结构的气动性能.此外，在设计风洞实验模型的时候，尽量保证模型外形与实际结构相似，尤其是倒角模拟的一致性，以免造成较大的误差.

5结论

1) 开源程序OpenFOAM模拟得到的方柱断面和不同攻角下主梁断面的静气动系数与实验结果能够较好的吻合，因此利用OpenFOAM研究桥梁断面气动性能是可行的.

2) 对于闭口箱型主梁断面，断面外形的细微变化会对其气动性能产生较大的影响.尤其是在正攻角下，下表面倒角会一定程度上抑制断面流动分离，大幅度的减小断面三分力系数，从而改善结构的气动性能.

3) 在设计风洞实验模型的时候，尽量保证模型外形与实际结构相似，尤其是倒角模拟的一致性，以免造成较大的误差.

参 考 文 献

[1]SIMIU E, SCANLAN R H. Wind effects on structures[M]. New York: John Wiley & Sons,Inc.,1996.

[2]郭震山.桥梁断面气动导数识别的三自由度强迫振动法[D].上海:同济大学,2006.

[3]周立,葛耀军.上海长江大桥节段模型气动三分力实验[J].中国公路学报,2007,20(5):48-53.

[4]VAIRO G. A numerical model for wind loads simulation on long-span bridges[J]. Simulation Modelling Practice and Theory,2003,11(5-6),315-351.

[5]SARWAR M W, ISHIHARA T, SHIMADA K, et al. Prediction of aerodynamic characteristics of a box girder section using the LES turbulence model[J]. J. Wind Eng. Ind. Aerodyn.,2008，96:1895-1911.

[6]应旭永,许福友,张哲.桥梁断面静三分力系数快速数值识别方法[C].第十六届全国结构风工程学术会议论文集,成都,2013.

[7]刘天成,葛耀军,曹丰产.桥梁断面静风荷载的格子Boltzmann方法数值计算[J].空气动力学报,2009,27(1):17-24.

[8]刘玥,陈政清,张志田.箱梁断面静风力系数的CFD数值模拟[J].振动与冲击,2010，29(1):133-137.

[9]MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J]. AIAA Journal,1994,32(8):1598-1605.

[10]应旭永.桥梁结构气动参数识别的数值模拟研究[D].大连：大连理工大学,2012.

ARGENTINI Tommaso2)Rocchi Daniele2)

(Department of Mechanical Engineering, Politecnico di Milano2)Mialno20133)

Research on the Aerostatic Characteristics of Bridge Deck Based on OpenFOAM

YING Xuyong1)ZASSO Alberto2)XU Fuyou1)ARGENTINI Tommaso2)ROCCHI Daniele2)

(InstituteofBridgeEngineering,DalianUniversityofTechnology,Dalian116023,China)1)(DepartmentofMechanicalEngineering,PolitecnicodiMilano,Mialno20133,Italy)2)

Abstract：Taking an Italian cable-stayed bridge as an engineering example, the aerostatic characteristics of closed-box deck section are investigated using both wind tunnel test and CFD numerical simulation. Based on the open source code OpenFOAM, the aerostatic coefficients and pressure coefficients distribution of square section and bridge deck section under different attack angles are numerically simulated. The simulation results are compared with the experimental data from the wind tunnel test. The effects of bottom surface chamfers on the aerostatic characteristics are also studied. Furthermore, the simulated wind flow around the box deck section is carried out to explore the mechanisms of the experimental results. The results show that the aerostatic coefficients of square section and bridge deck section under different angles of attack obtained from the test and the simulation match well. The aerostatic performance of closed-box deck section can be improved by using a rounded chamfer on the bottom surface.

Key words：numerical simulation; OpenFOAM; bridge section; aerostatic characteristic; aerostatic coefficient

收稿日期：2016-03-11

中图法分类号：U441.2

doi:10.3963/j.issn.2095-3844.2016.03.009

应旭永(1987- ):男，博士生，主要研究领域为桥梁风工程

*国家自然科学基金项目资助(51478087)