无缝喷气襟翼特性研究与设计优化*
陈 功
(中国商飞上海飞机设计研究院总体气动部 上海 201210)
无缝喷气襟翼特性研究与设计优化*
陈功
(中国商飞上海飞机设计研究院总体气动部上海201210)
摘要:根据二元翼型的流动控制原理,在无缝襟翼的基础上增加了喷气装置形成无缝喷气襟翼,可使翼型的最大升力系数CL,max进一步提高.为了研究该技术使用的可行性,通过CFD仿真计算并结合控制变量法分析了不同喷射角θ、喷口高度h、喷射速度V对最大升力系数CL,max的影响及规律.通过建立数学模型,并采用遗传算法对该无缝喷气襟翼的方案进行了优化设计.研究表明,使用喷气襟翼技术并选择合适的设计参数可以使二元翼型的最大升力系数得到了明显提高.该种新概念可以作为民用飞机增升装置研发的重要发展方向.
关键词:无缝襟翼;流动控制技术;遗传算法;CFD仿真
0引言
襟翼作为机翼增升装置的一部分,通常位于主翼后缘.襟翼在飞机的起降阶段提供额外的升力,是重要气动元件.无缝襟翼是襟翼的一种,一般采用形内定轴转动的作动方式.其优点在于运动轨迹简单,作动系统简明,机械结构轻便,能显著地降低飞机的结构重量和控制复杂程度[1].然而,在当前大型民用客机设计研发领域,无缝襟翼尚未获得广泛的运用.相关研究表明[2],尽管无缝襟翼在减轻重量、优化结构上具有优势,但在气动性能上却有明显短板.与常规的单缝/双缝襟翼相比,采用无缝襟翼方案时下翼面的气流无法通过缝道对上翼面边界层进行能量补充.在迎角变大时,上翼面气流分离现象较明显,导致气动性能衰减过快.
根据当前空气动力学的发展,在使用无缝襟翼的基础上引入流动控制技术是解决这一问题的有效手段.采用流动控制技术的无缝襟翼简称“无缝喷气襟翼”,即从发动机处将气源引流至无缝襟翼前缘处的喷气口对外进行“喷气”,以此对翼面下游边界层进行能量补充,同时对机翼的绕流进行加速,提高环量.实现改善机翼上表面气流分离,提升最大升力的目的[3-4].
为了验证无缝喷气襟翼技术的可行性,将以典型的二元机翼截面(参考弦长为4 m)为研究对象,采用CFD仿真计算的研究“喷气”的影响.并在此基础上采用遗传算法对该喷气襟翼进行方案优化设计.
1问题描述
1.1“无缝喷气襟翼”原理
当襟翼偏度确定后,采用“无缝喷气襟翼”技术可保证在不大幅度改变翼型几何外形及整体结构的前提下,通过对绕翼型的流动控制,实现对翼型升力特性的改善.
常规的无缝襟翼上翼面后缘处的气流容易出现“分离”现象,造成升力损失.见图1.

图1 常规无缝襟翼分离现象
采用“喷气”技术后,当气流从上翼面开始分离或有分离趋势时,自喷口处喷出的气流对上翼面边界层进行能量补充;同时加快了翼型周围绕流的速度,产生较大的环量,从而提高了最大升力系数CL,max[5-6].见图2.
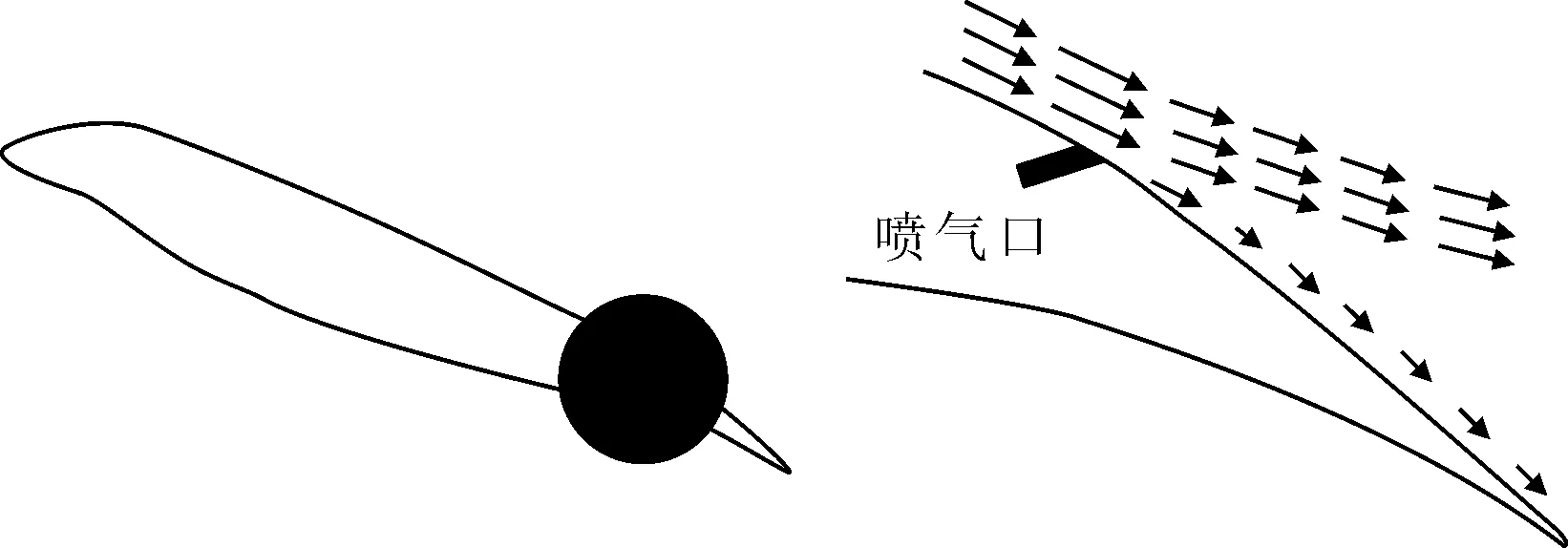
图2 无缝喷气襟翼原理
1.2设计参数
设计参数的选择是否恰当将直接关系到设计过程的合理性和结果的可靠性.
常规的单缝襟翼涉及众多缝道参数,包括(不仅限于)后退量κ、下沉量η、缝道宽度Ω、扭转角ψ等,缝道参数的设计过程复杂,牵涉面广,工作量庞大.见图3.

图3 二维常规单缝襟翼缝道参数示意图
与常规的单缝/双缝襟翼相比,无缝喷气襟翼在设计时无需考虑众多缝道参数,显著地降低了设计的复杂程度.但由于加装了喷气装置,其设计变量应予以仔细考虑.设计参数见图4.

图4 无缝喷气襟翼主要设计参数示意图
图中:T为气流自喷口射出时的初始温度;喷口位置c%为喷口弦向所在位置,一般位于主翼后梁处,襟翼前缘;喷射角度θ为喷射方向与襟翼上翼面轮线廓夹角;喷口高度h为喷口截面的宽度,一般为弦长1%~2%;喷射速度V为气流自喷口喷出时的初速度,一般为亚音速流动条件.
其中,喷口位置c%与气流温度T分别取决于机翼内部空间结构与发动机特性等多方面因素,牵涉系统较多,无法轻易变动,故不在现阶段研究范围内.而喷口高度h、喷射角θ、喷射速度V为局部变量,对机翼主体结构影响较小,设计余地较大,将作为当前研究的主要设计参数.
1.3设计目标
“喷气”技术主要用于飞机起降阶段,该阶段最关注的气动性能为最大升力系数CL,max.提高最大升力系数可以有效地提高飞机的爬升率,缩短爬升时间;同时,较大的升力系数可以显著降低着陆时的滑跑速度,降低对着陆场长的需求.故尽可能大的CL,max应视为无缝喷气襟翼的重要设计目标.
另外,由于“喷气”所用气源引自发动机处,对能源形成了一定程度的消耗.为了确保该技术的经济性,在重点关注CL,max的同时,还应同时关注能量耗散Ec,尽可能将其控制在合理的范围内.
2研究方法
2.1网格生成
在研究二维流场问题之前,通常需对流场的物理域进行空间离散,即通过网格划分将连续的物理流场“打散”成离散的计算域,以便采用CFD(computational fluid dynamic)仿真手段对其进行数值求解.网格划分的合理性与质量将直接关系到最终的计算结果.见图5.

图5 网格生成
该带有无缝喷气襟翼的二元翼型所处于的流场采用ANSYS-ICEM14.0软件生成不少于80万的四边形结构化网格进行划分.为了适配CFD计算中所采用的壁面模型,对二元翼型壁面处的网格进行了适当的加密处理,便于捕捉流场细微的变化.另外,为了提高对“喷气”处仿真计算的准确性,对该区域的网格也进行了加密处理.
2.2CFD仿真
对二维流场的数值计算一般需借助于成熟的仿真软件,该研究将采用ANSYS-Fluent14.0软件对该二元翼型的流场进行仿真计算.模拟主要针对马赫数Ma=0.2的低速飞行状态,计算采用二维定常可压缩流动雷诺数加权平均N-S控制方程(RANS)结合单方程SA湍流模型,并采用有限体积法进行离散,选用基于压力的耦合隐式求解器结合高斯塞德尔迭代法进行数值求解.
流场边界初始条件为压力远场(far pressure inlet),初始压力值p0=100 kPa,远场来流恒定速度U0=70 m/s(Ma=0.2),雷诺数Re=6 000 000;喷口设定为压力入口(pressure inlet),根据不同的计算条件设定喷射速度V.其余上下翼面及喷射通道的边界条件均作固壁(wall)设定.
3计算结果分析与讨论
为了研究1.2中3个设计参数对无缝喷气襟翼气动性能的影响,将采用控制变量法对CFD的计算结果进行规律性分析.文中所列各数据与曲线均已进行去跳点,求平均,多项式拟合等必要的修正.
3.1喷射角θ对升力的影响
保持喷口高度h=2 cm,喷射速度V=70 m/s的条件不变,分别计算喷射角为θ=2°,8°,14°时翼型的升力特性曲线,结果见图6.

图6 喷射角θ对升力的影响
分析比较图6中各曲线之间的规律可知,选择适当大小的喷射角θ有助于地提高最大升力系数CL,max,但θ越大,最大升力提高的幅度越小.过大的喷射角非但不能提高最大升力系数,相反还会降低原有CL,max.分析其原因见图7.

图7 喷射气流矢量分解
当气流被喷出后形成Vcosθ,Vsinθ两个分量.Vcosθ分量顺翼型表面向下游流动,对边界层进行补充,有利于气动性能的改善;而Vsinθ分量垂直翼型表面向外流动,更容易促使翼面气流分离,导致气动性能的下降.当θ增大,Vcosθ分量减小,Vsinθ分量增大,致使增升效果受到影响.
3.2喷口高度h对升力影响
保持喷射角θ=3°,喷射速度V=70 m/s不变,分别计算喷口高度为h=4,6,8 cm时翼型的升力特性曲线,结果见图8.
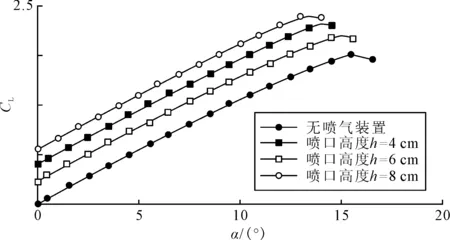
图8 喷口高度h对升力的影响
从图8中可知,在相同条件下,喷口高度h越大,最大升力系数CL,max越大.结合空气动力学理论分析可知,较高的喷口可以确保喷出的气流足够“厚”,能对下游襟翼上翼面边界层进行更充分的能量补充,缓解翼面气流分离导致的升力损失,从而提高最大升力系数.
3.3喷射速度V对升力影响
保持喷射角θ=3°,喷口高度h=6 cm不变,分对计算喷射速度为V=70,105,140,175 m/s时翼型的升力特性曲线,结果见图9.

图9 喷射速度V对升力的影响
从图9可知,喷射速度V越大,最大升力系数CL,max越大.结合空气动力学理论分析可知,射出气流越“快”,所携带的动能越大,对周围流场“加速”效果越明显,更有效地增加绕翼型环量,从而提升最大升力系数.
4设计优化
上文中对升力特性曲线中已总结出喷射角θ、喷口高度h、喷射速度V3个设计参数对喷气襟翼气动性能影响的规律.但在实际设计过程中,要考虑的是3个设计参数耦合后的影响.由于3个设计参数经排列组合后将产生数百种不同方案,如一一进行计算,将耗费不必要的时间和计算资源.因此引入优化计算方法来提高计算效率非常重要.
4.1遗传优化算法
为了简化问题并提高计算效率,在进行CFD仿真的同时引入遗传算法对计算过程进行优化.遗传算法是一种综合并行、取样、自适应的算法,具有全局优化的优点,适用于处理离散、多参数一体化设计问题.遗传算法的原理及流程见图10.

图10 遗传算法原理图
4.2数学模型建立
1) 变量及其定义域如表1所列,该数学模型中的变量与设计优化问题中的设计参数一一对应.变量的定义域与设计参数的许用范围一致,定义域由设计问题本身的约束决定,如机翼内部结构空间,气源能量限制等.

表1 变量与定义域
注:按排列组合计算,计算样本总共13 340.
2) 目标函数及期望值根据1.3中的论述,最大升力系数CL,max将作为喷气襟翼的主要设计目标即目标函数;由于无缝喷气襟翼所使用的气源来自于发动机,因此需控制气源所需的总能量,避免不必要的浪费.根据以上各要素,结合型号飞机实际需求,确定目标函数如下:
Ec=0.5ρv2h≤[Er]
式中:CL,max≥2.5的要求取决于对飞机起降性能(跑道限长,爬升率等)要求;能量耗散限制[Er]取决于对发动机能量耗散的要求.两者均来源于型号设计要求,此处不做详细阐述.
4.3优化结果
按如图9所示的遗传算法选出样本并对其进行CFD计算获取CL,max,并同时计算Ec.仅经过100次取样后就已获得了3个样本满足目标函数的期望值,见表2.

表2 满足要求的样本
注:以上结果筛选自前100次迭代计算.
表2中所列举的3个样本均满足目标函数的期望值,即说明采用表2中所列的3种设计参数组合可使最终结果满足相关的气动性能.如需要,可继续使用优化算法结合CFD计算在设计参数的定义域内获得更多符合条件的样本.
5结 束 语
通过对喷气襟翼不用设计参数的研究可知,减小喷射角θ,增大喷口高度h, 增大喷射速度V,均有利于提升“喷气”的效果,提高翼型的最大升力系数,从而发挥“无缝喷气襟翼”的优势.
在解决类似该种“多参数一体化设计”问题时,采用遗传优化算法将工程设计问题转化为数学模型问题进行计算和分析可以节省了大量的计算时间和资源,使复杂问题简单化,程序化,大大提高了工作效率和针对性.
值得注意的是,以上对“无缝喷气襟翼”的特性分析及设计优化的研究均基于二元翼型层面,其结论具有一定的规律性和普遍性,适用于“无缝喷气襟翼”设计的初步阶段.在后续的研究中,可将以上规律性结论和研究方法推广至实际三维机翼设计研发中.
参 考 文 献
[1]程庆玉,焦予秦.喷气吹气襟翼对翼型气动影响研究[J].航空计算技术,2006,36(1):101-102.
[2]郝南松,杨文超,杨基明.低Re数下变弯度机翼的非定常气动特性实验研究[J].实验力学,2014,29(3):294-300.
[3]倪云华,杨爱明,翁培奋.低雷诺数下微型飞行器主动变形机翼非定常气动特性数值分析[J].空气动力学学报,2006,24(3):307-313.
[4]杨文超,杨剑挺.变弯度机翼准定常流动分离特性的实验研究[J].中国科学,2012,42(5):531-537.
[5]焦予秦,陆岩.多段翼型吹气流动分离控制研究[J].应用力学学报,2015,32(2):215-220.
[6]陈钱,白鹏,刘子强.可连续光滑偏转后缘的变弯度翼型气动特性分析[J].空气动力学学报,2010,28(1):46-52.
Characteristics Analysis and Design Optimization of Blowing Seamless Flap
CHEN Gong
(ShanghaiAircraftDesignandResearchInstitute,GeneralIntegrityandAerodynamicsDepartment,Shanghai201210,China)
Abstract:According to the flow control theory of 2D-airfoil, blowing seamless flap is generated by applying jetting-nozzle on seamless flap, which is able to improve the maximum lift coefficient (CL,max). To ensure the feasibility of this technology, CFD simulation is conducted to calculate CL,maxdue to different blowing angle θ, nozzle height h and blowing velocity v with the method of “Control Variables”. After that, the method of “genetic algorithm” combined with the mathematical model is utilized for design and optimization. The result illustrates that CL,maxis obviously improved by applying technology of “blowing flaps”. Such innovative concept can be used in following research of civil aircraft high-lifting devices.
Key words:seamless flap; flow control technology; genetic algorithm; CFD simulation
收稿日期:2016-04-23
中图法分类号:V211.4
doi:10.3963/j.issn.2095-3844.2016.03.005
陈功(1986- ):男,博士,工程师,主要研究领域为工程结构与力学
*国家中长期科学和技术发展规划纲要(2006-2020年)大飞机专项资助

