湖南武陵山片区金融资源集聚与经济增长研究

廖凯诚，彭 耿，刘 芳，王 昊

（吉首大学 商学院，吉首416000）



湖南武陵山片区金融资源集聚与经济增长研究

廖凯诚，彭 耿，刘 芳，王 昊

（吉首大学 商学院，吉首416000）

摘要：贫困地区经济增长的影响因素研究是当前研究的热点，但鲜有文献从金融资源集聚的角度去探讨。本文利用2003-2011年湖南武陵山片区面板数据，利用固定影响变系数模型和混合广义最小二乘（Pooled EGLS）估计法进行实证研究。研究结论表明：湖南武陵山片区金融集聚程度与经济增长之间呈现同期反向变动的关系，且各地区的金融集聚程度对本地区的经济增长影响不显著，多数地区的金融集聚程度与经济增长成负相关，同时从三个层面分析了这一现象出现的原因。

关键词：金融集聚；经济增长；固定影响变系数模型；混合广义最小二乘法

1　引言

2010年，中央把集中连片特殊困难地区（以下简称“连片特困地区”）作为新阶段扶贫攻坚主战场的战略部署和国家区域发展的总体要求，决定率先启动武陵山片区区域发展与扶贫攻坚试点工作，为全国其他连片特困地区提供示范。武陵山片区地处湖北、湖南、重庆、贵州四省市交界处，覆盖71个县（市、区），总面积达17.18万平方公里，其包括湖北11个县市、湖南37个县市区、重庆市7个县区、贵州16个县市。2011年末，总人口3578.41万人，城镇人口占比28.59%，农村人口占比71.41%。本文选取湖南省34个县市区作为研究对象（其中，鹤城区、洪江市、新化县由于数据的缺失被剔除），从相关经济发展数据来看，2003-2011年间，整个湖南武陵山片区的年末金融机构贷款总额从2003年的356.94亿元扩大到2011年的1009.14亿元，平均每年以12.24%的速度增长，人均GDP总额从2003年的144749元以年均16.45%的发展速度快速增长，到2011年达到569952元，而社会消费品零售总额、财政支出、规模以上工业总产值以及社会固定资产投资额年均增长速度分别为14.44%、23.08%、29.16%以及24.78%。在过去的9年里，湖南武陵山片区经济发展总体趋势良好。从上面数据分析可知湖南武陵山片区经济金融都获得了快速的增长。众所周知，金融资源是经济生活中国民财富的核心，是经济发展的动力源泉。但湖南武陵山片区金融资源对经济增长的影响方向与程度还未有学者进行讨论，因此，本文将探讨湖南武陵山片区金融资源集聚与经济增长之间的关系，这可为合理配置金融资源，促进区域经济增长，以及协调金融与经济发展提供重要依据。

2　文献回顾

近年来，一些研究者开始从金融的视角去探索区域经济增长的内在机制。通过对相关文献的梳理发现，研究者借鉴金融发展理论的观点，在经济增长模型中引入金融因素来表明金融发展水平与区域经济增长有着密切的联系。如，赖娟（2013）运用多元线性回归模型，实证研究了江西省金融发展与经济增长之间的关系，研究发现：影响江西经济增长的不仅仅是金融发展规模，还有金融发展效率，而且金融发展规模与江西经济增长之间存在显著的因果关系和正相关关系［1］。陆静（2012）根据中国省际面板数据，采用面板单位根、面板协整和向量误差修正模型实证分析了金融对于中国经济增长的影响，研究表明：金融发展程度不仅是经济增长的Granger原因，还对经济增长具有明显的正向推动作用［2］。虽然金融增长能够促进经济增长，但金融发展的内在质却只能由经济增长所引致（武志，2010）［3］。而韩廷春（2003）认为:只要金融部门的效率在不断提高以及无形资本的水平在不断增长，则经济的持续增长就成为可能［4］。冉光和李敬（2006）等人发现在不同的区域条件约束下，金融发展与经济增长之间的关系可能不会稳定一致［5］。这一观点得到了马轶群和史安娜（2012）的证实，他们认为金融发展与经济增长方式质量和经济增长稳定性不存在长期稳定关系，并且金融发展对经济增长协调性呈现出短期增强和长期是弱化的影响［6］。还有学者认为由于地域的差异性，金融发展对地区的经济增长表现出不同的作用，有些地区的金融发展甚至不利于该地区的经济增长。如，梅丹和周松（2008）的研究表明，我国城市金融发展与其经济增长间是负相关关系，同时不同区域位置和不同规模城市间金融发展对经济增长作用有显著差异［7］。

国内外另一些学者用金融发展的观点来解释地区收入分配差距，整理相关文献发现有以下几种观点。其中部分学者认为金融发展与收入差距之间存在着库兹涅茨效应，就是所谓的倒U型关系。如，陈伟国和樊士德（2009）在对中国金融发展水平与城乡收入分配之间的关系进行检验时发现金融发展和城乡收入差距之间存在着库兹涅茨倒U型关系［8］。李志军和奚君羊（2012）也认为在金融发展的初期，其对收入差距具有扩大效应，而在金融发展达到一定程度，收入差距就会随之缩小，即金融发展与收入差距之间存在倒U关系［9］。刘朝阳和梁惠娟（2014）等从宏观、中观和微观视角对金融发展影响收入分配的机制进行研究，发现越是欠发达地区，金融规模的提高越会缩小城乡收入差距，在经济相对发达的地区，金融效率的提高对收入差距的缩减效应更明显，同时金融发展与城乡居民收入差距存在库兹涅茨效应［10］。第二种观点认为金融发展有利于改善收入分配不平衡程度缩小贫富差距，Clarke & Xu （2003）等人利用全球91个国家1960-1995年的数据实证研究了金融部门发展和收入差距之间的关系，发现金融发展会显著降低一国收入分配差距［11］。对于金融发展规模的提高能有效抑制贫富分化，于潇和王学龙（2011）等人给出了自己的解释，他们认为资本的货币化能够使单个资本在一定程度上超越种类和规模的限制，特别是金融发展将进一步促进这种超越，从而有助于抑制贫富分化［12］。第三种观点则认为金融发展会加剧收入分配的不平等扩大贫富差距，持这种观点的人主要是国内学者，他们利用中国现有的数据进行实证研究，得出了自己的结论。温涛和冉光和（2005）等人在对中国金融发展与农民收入增长进行制度和结构分析的基础上，利用1952—2003年的实际数据实证研究了中国整体金融发展、农村金融发展与农民收入增长的关系。研究发现:中国金融发展对农民收入增长具有显著的负效应［13］。杨俊和李晓羽（2006）等人的研究结论显示我国金融发展显著扩大了全国、农村以及城乡居民收入不平等程度［14］。

随着金融发展的深入研究，研究者结合地理因素在考察金融问题时发现，在适宜的地域或空间内金融资源通过与地域情况相结合参与地域运动凝结成金融产业，进而形成金融集聚，但由于地域差异，使金融资源会流向条件优越的地区，从而导致各区域的金融集聚存在差异（刘红、叶耀明，2007）［15］。然而，在现有金融集聚的文献中，有关金融集聚与区域经济增长关系的相关研究相对不足，同时将视角聚焦于武陵山片区的区域经济增长的研究更为缺乏。鉴于此，本文参考已有的文献，以湖南武陵山片区为例，利用2003-2011年的面板数据采用固定影响变系数模型进行实证分析。

3　研究方法与模型构建

3.1区位商

国内外众多学者研究某一产业聚集程度时，常用空间基尼系数、产业集聚指数、哈莱一克依指数以及区位商指数这四种方法。其中，空间基尼系数的缺点在于，没有考虑企业规模分布对产业地理集中的影响，而产业集聚指数虽然是在基尼系数的基础上进行了改进，但仍然没有排除产业内企业规模的影响。哈莱一克依指数由于需要运用高深的数学方法进行计算得到，相对复杂难懂［16］。区位商又称专业化率，是衡量区域某产业专业化水平的指标，并得到了长期的使用。为更好的将湖南地区金融集聚程度量化，又结合各项数据的可得性原则，把区位商计算公式做了合理的改动为：

公式（1）中，Pit为i地区第t年的区位商，hit为i地区第t年的金融产业值，本文用该地区的年末金融机构贷款余额表示该地区的金融产业值。eit为i地区第t年的第三产业的总产值。Ht为第t年湖南武陵山片区的金融产业总值，Et为湖南武陵山片区第三产业总产值。如果Pit＞1，那么，金融集聚程度比较高，金融产业在该地区比较有优势，竞争力就越强。Pit值越大，专门化程度越高，该区域的金融产业优势越充分。

根据这一思想，可以计算出在过去9年湖南武陵山片区的各个县市金融集聚程度的平均值。其中，花垣县的金融集聚程度为2.195，排名第一，而吉首市的金融集聚值为1.924，暂居第二，中方县金融集聚值最低仅为0.399，其次是会同县，它的金融集聚值为0.486。金融集聚值大于1的县市有14个，如，城步县、永定区、泸溪县、永顺县、新邵县、龙山县、保靖县、石门县、冷水江市、武陵源、慈利县以及辰溪县，金融集聚值低于1的大部分县市均值均在0.8到0.97范围内，个别县市的值低于0.8，例如，新晃县为0.737、凤凰县为0.701，芷江、邵阳、靖州的金融集聚值分别为0.665、0.648以及0.544。

为了更加客观的观察湖南武陵山片区金融集聚程度与经济增长的关系，本文将用人均GDP增长率（环比法）代替经济增长率，同样用环比法求出湖南武陵山片区的金融集聚度增长率（图1）。

从图1可以看出湖南武陵山片区金融集聚程度与经济增长是同期反向变动，而经济增长和金融集聚程度的变动呈现出波峰波谷交替变动的趋势，即循环变动。

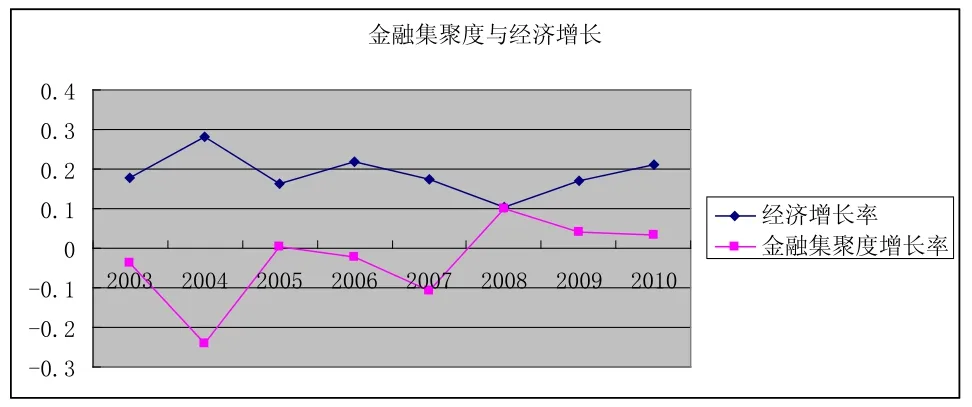
图1　湖南武陵山片区金融集聚度与经济增长

3.2模型构建

为分析金融集聚程度对该地区经济增长的影响程度，本文构建的模型如下：

他开始摸索自己的盲品攻关套路。“平均每款酒只有大概11分钟，那我会规定自己必须每款酒都在8分钟内完成。我会看着时间，如果到点，我就必须跳到下一组题。这样每款酒的时间都缩短，最后你还有十几分钟剩。这跟跑步差不多，如果你定的目标是5公里，但可能你到4公里就跑不下去了，但如果你目标是8公里，那跑5公里就比较轻松了。”朱利安总结道，随后有点羞涩地笑着说：“我每次还是会超时。不过，可能写不完，但基本上也不会再超十几分钟了。”

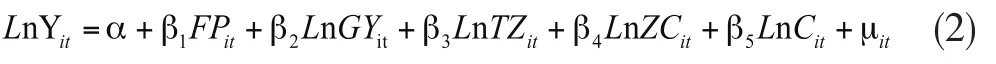
其中，Yit为人均GDP，基于参考大多数文献选取人均GDP代替反映经济增长更为合理也便于获取，为了控制变量的尺度和和计算的方便性，同时消除部分异方差问题，故对人均GDP取对数。FPit表示i区域第t年的金融区位商值，以此来衡量该地区的金融集聚程度，由于该值为比值形式故不做对数处理。为剔除其他因素对经济增长的影响，本文选取了其他4个变量作为控制变量1。其中，LnGPit表示i区域第t年的人均规模以上工业总产值取对数，以此来衡量该地区的人均规模以上工业总产值对经济增长的贡献。LnTZit衡量i地区第t的人均固定资产投资取对数，是用来考察人均固定资产投入量带来的经济增长的影响。LnZCit表示i地区第t年的人均财政支出取对数，以此衡量人均财政支出对经济增长的影响。LnCit表示i地区第t年的人均社会消费品零售总额取对数，用于观测人均消费对该地区增长的影响。

本数据来源于《湖南统计年鉴》部分数据来源于各县市统计公报，本文分析了湖南武陵山片区34个县市地区2的金融聚集、规模以上工业总产值、固定资产投资、财政支出以及社会消费品零售总额对经济增长的影响，各数据的描述性统计分析结果如表2。

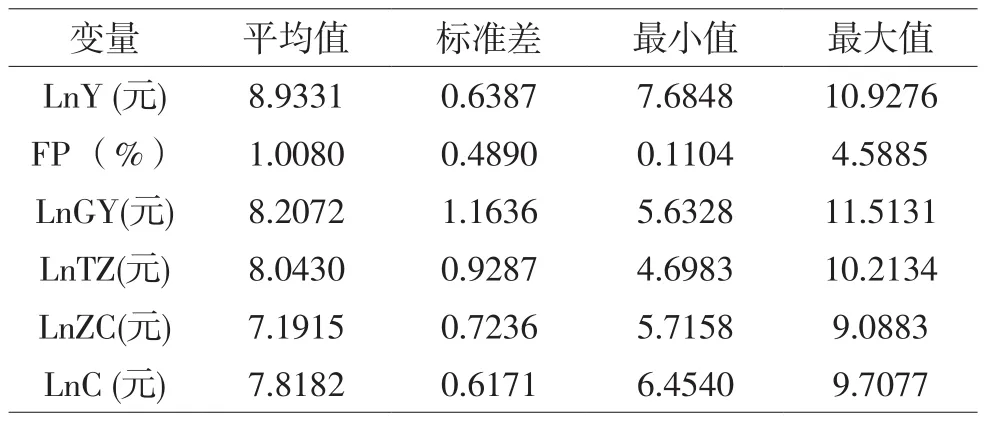
表2　描述性统计分析结果

4　回归结果

4.1面板数据检验

4.1.1单位根检验

为了避免伪回归问题，我们在进行时间序列分析时会通过单位根检验对数据平稳性进行判断。然而，面板数据单位根的检验主要有Levin、Lin &Chu 方法（LLC 检验）、Im、Pesaran and Shin W-Stat 方法（ IPS检验）、ADF-Fisher Chi-square方法（ADF检验）和PPFisher Chi-square方法（PP检验）等方法3。实证过程我们首先对各变量分别进行以上四种方法单位根检验，结果见表3。

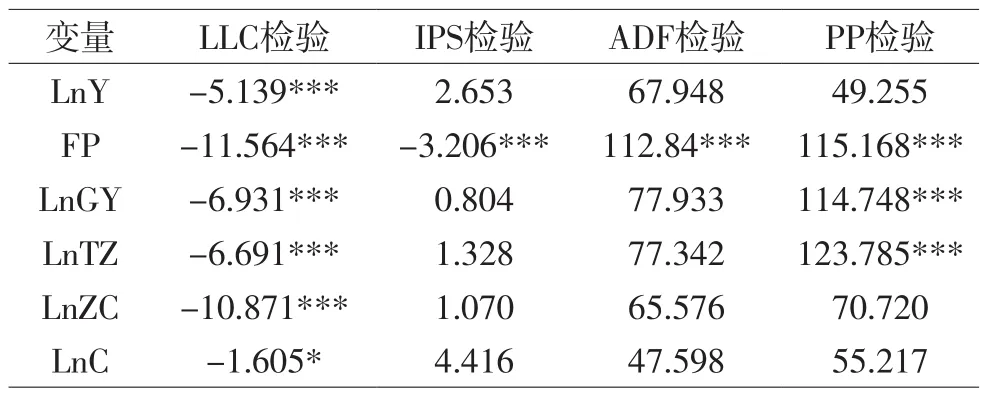
表3　单位根检验结果

从表3中的LLC检验结果表明所有变量在1%和10%显著性水平下不存在同质面板单位根，然而从IPS、ADF、PP检验来看LnZC、LnC、LnY检验结果表明存在异质面板单位根。LnTZ、LnGY在1%显著性水平下不存在异质面板单位根的原假设。其中FP通过了所有检验说明该变量序列平稳。

综上所述：我们可以得出LnTZ、 LnGY、FP是平稳序列，LnZC、LnC、LnY为非平稳序列，需要进一步对变量做差分再对差分后的结果进行平稳性检验。变量差分后的平稳性检验结果如表4。

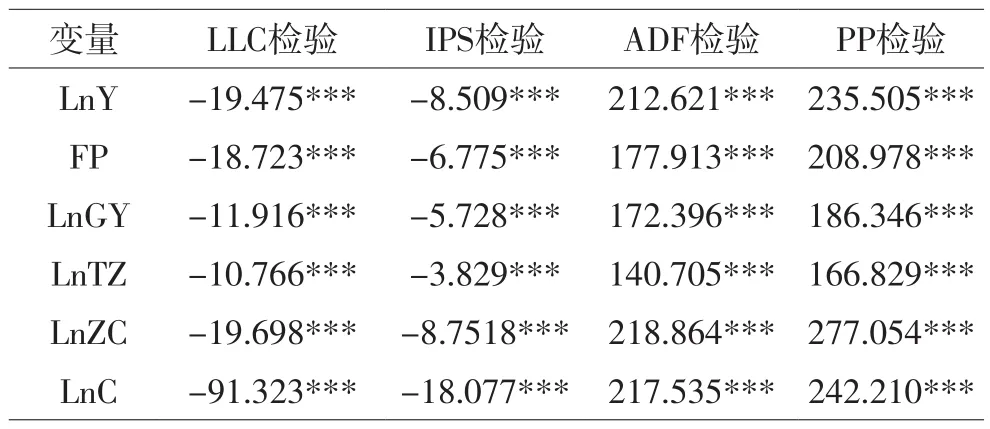
表4　一阶差分后平稳性检验结果

从表4的检验结果可以看出，变量经过一阶差分后序列为平稳序列，LLC检验显示在1%显著性水平下各变量不存在同质面板单位根，在IPS、ADF及PP检验结果显示在在1%显著性水平不存异质面板单位根。总之，从不同面板单位根检验可以得到基本一致的结论：各变量经过一阶差分后都是平稳的，即各变量为一阶单整I（1）。

基于上述单位根检验我们发现变量之间为一阶单整，那么我们可以进行协整检验，以确定各变量之间的长期联系。早在1987年Engle和Granger提出的协整理论为非平稳序列的直接建模提供了一种非常有用的途径，其基本思路是：对于非平稳序列，如果它们的线性组合可以构成平稳序列，此时我们称这些变量序列间有协整关系存在。目前，检验面板数据的协整关系的方法主要有（1） Kao（1999［17］；2000［18］）构造的DF和ADF检验。（2）Pedroni（2004）［19］构造的7个检验面板协整关系的统计量4［20］。为了保证结果的稳健性，本文将进行Kao方法检验并报告ADF统计量和Pedroni方法检验并报告全部统计量，检验结果如下：

表5　协整检验

从表5可知，Pedroni 检验的七个统计量和 Kao 检验2的统计量在1%显著性水平上拒绝不存在协整关系的原假设，这充分表明各个变量之间存在协整关系。4.1.3模型设定

本文对最终计量模型的选定包含两个方面（1）首先采用F检验确定模型形式，先进行变系数模型5的检验，其原假设H0：（即不变系数模型）。检验的F统计量为：

其中，RSSR为受约束模型6（即混合回归模型）的残差平方和RSSures为变系数模型的残差平方和。N为截面数目，T为时间数目，K为解释变量的个数（同下）。其计算结果RSSR=12.21674，RSSures=0.326095，N=34，T=9，K=5，则F=18.784＞F0.01（198，102）=1，故在1%的显著性水平下拒绝不变系数的原假设，该模型确定为变系数模型。

再对模型进行混合回归模型和固定影响模型的检验。其原假设H0：混合回归模型，检验的F统计量为：

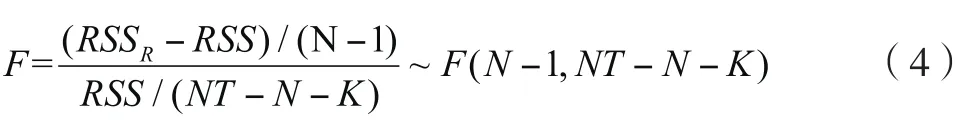
RSSR为受约束模型（即混合回归模型）的残差平方和，RSS为最小二乘虚拟变量模型的残差平方和（即固定影响模型）。其计算结果为：RSSR=12.21674 ，RSS=2.284277，N=34，T=9，K=5则F=35.181＞F0.01（33，267）=1.7，故在1%的显著性水平下拒绝原假设，将模型设定为固定影响模型。

（2）采用Hausman检验，进行固定影响模型和随机影响模型的确定，其原假设H0：随机影响模型 H1：固定影响模型，Hausman检验结果如下：

表6　Hausman检验结果

由表6可知，在1%显著性水平下，拒绝原假设H0：随机影响模型，选择固定影响模型比较好。

综上所述，基于本文研究对象的特性，加之使用截面数据中N（截面单元的数目）大于时间长度T（时间序列数据的数量）模型设定和估计更加侧重于截面分析，因此我们最终将模型设定为固定影响变系数模型，估计方法我们通过横截面加权的方法采用面板广义最小二乘估计（即Pooled EGLS），估计结果如表7。

协整检验结果显示，各变量之间存在长期均衡关系（即协整关系），那么我们对变量进行估计其结果是可信的。为研究金融集聚程度对该地区经济发展的影响，我们着重分析FP（金融集聚程度系数）的数值。从表7中我们发现，大部分县市金融集聚程度对经济增长的影响是不显著的，而且与经济增长成负相关，这与部分学者的研究是相一致的，如邓永亮等（2010），在VAR模型的基础上，采用我国年度数据，研究发现:长期内，金融发展阻碍经济增长，而通货膨胀促进经济增长；短期内，金融发展对经济增长影响不显著，通货膨胀对经济增长影响显著［21］。如果把那些有可能影响经济增长的相关因素都考虑在内的话，换句话说，如果我们对经济增长进行多元回归分析的话，那么信贷比重与经济增长之间的负相关关系就会更加显著（张军，2006）［22］。

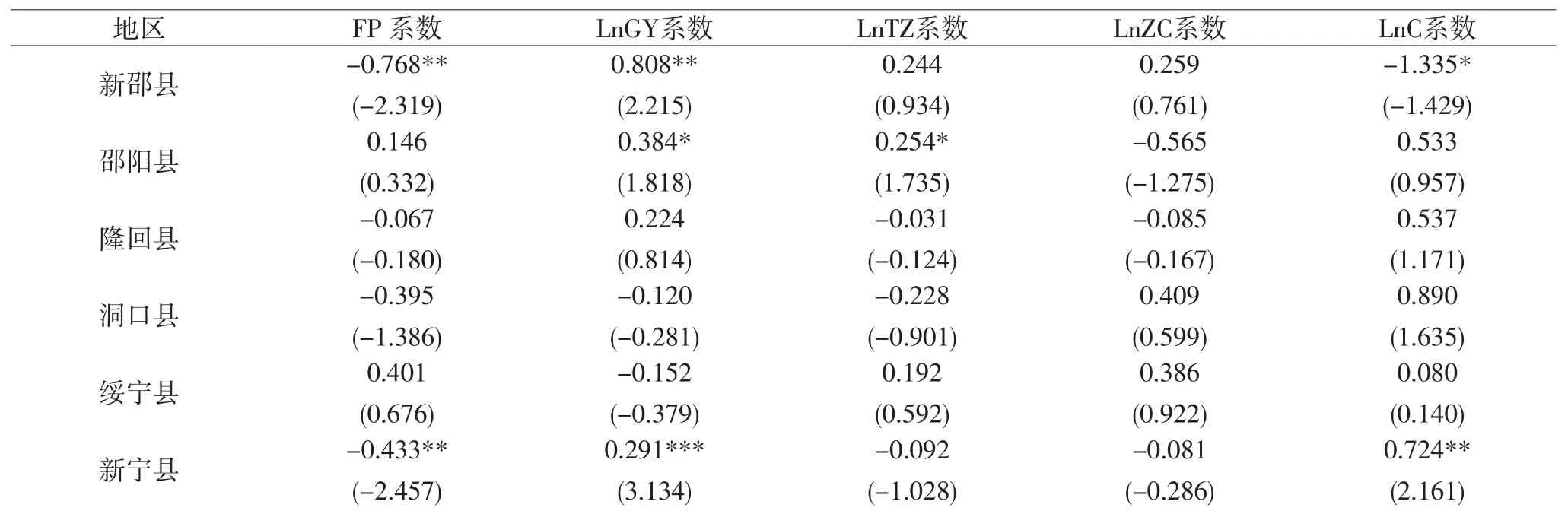
表7　Pooled EGLS估计结果

注：***、**、*分别表示在1%、5%和10%的显著性水平上通过统计性检验，结果保留至小数点后三位

在分析中还显示，绝大多数县市的社会消费品零售总额的系数与经济增长是正相关，这说明该地区还是主要依靠消费来拉动经济的增长，特别是在几个旅游胜地，如，石门县、中方县、会同县、吉首市、凤凰县、龙山县，它们的消费系数都大于1，对比发现这些地区的金融集聚程度都没有有力的拉动经济增长，反而有些地方还阻碍的经济增长比如石门县、中方县、吉首市、以及凤凰县。再从规模以上工业总产值系数分析会发现，除小数几个县市以外，绝大多数规模以上工业总产值系数为正，这说明大部分地区的经济增长是靠工业带动，即规模以上工业总产值对GDP的贡献是巨大的。这是符合经济现象的，然而从政府支出来看，大部分各县市的政府支出都有利于经济增长，这说明政府的支出投入到基础设施建设对本地区的GDP增长带来的正向效应，为本地区的发展做出了贡献。

5　结论与政策建议

本文从金融资源的角度分析了湖南武陵山片区金融集聚程度对各个县市的经济增长的关系，研究结果表明各个县市的金融集聚程度对经济增长存在明显的差异，而对于绝大多数地区金融集聚程度对该地区的经济增长的影响不显著，金融集聚程度与经济增长的关系成负相关。从新古典经济学理论上说，金融的发展可以从外生动力和内生动力两个层面来推动地区的经济发展，外生动力通过政府对该地区的优惠和倾向政策，外生的驱动金融资源和金融机构在该地区形成金融中心，然后运用规模经济和辐射效应等促进该地区的经济增长，而内生动力（即需求型动力）是随着社会经济的发展，自然的产生了某些金融需求，从而驱使金融资源和金融机构在该地区聚集形成金融中心从而促进经济增长。因为金融机构聚集在很大程度上提高跨地区的支付效率和金融资源跨地区的配置效率，节约周转资金、提供融资和投资便利，有效地降低交易成本，促进各金融机构及各行业的信息交流（Kindleberge，1974）［23］，更有利于服务该地区的经济发展。那么，为什么本文的研究结果显示湖南武陵山片区各县市金融集聚程度对经济增长的影响是不显著而且大部分地区对经济增长的影响是有阻碍作用？笔者认为原因有如下三点：第一，从湖南武陵山片区的特殊地理环境来说，部分地区由于经济产业发展相对单一，经济发展相对落后，金融集聚程度底，金融资源得不到合理的开发，导致金融资源流失，即金融资本未能在内部循环而是转而流向经济条件更为优越的地区。第二，从湖南武陵山片区的生产要素的角度来看，由于地区的相对特殊性，导致了交通的不便捷，大量的劳动力人口流失，导致该地区的生产要素的流失，从而导致金融机构的贷款得不到有效率的应用。第三，虽然金融机构能够降低交易成本，提供融资和投资的便利，实现规模经济，但对一个区域的可能承受能力来说，当该地区的规模经济过度膨胀将会导致规模不经济，甚至影响该地区的发展。本文的研究意义在于，解释了在贫困地区金融资源并不一定能促进该地区的经济发展，为政府对贫困地区制定相关的金融政策提供帮助。当然，本文仅以湖南省武陵山片区为研究对象，如以整个武陵山片区为考察对象进行对比分析，其结论将会更具说服力。

注释：

1 由于数据的局限性，控制变量中未为引入就业人口（此变量用来考察人力资本对经济增长的影响），这是该模型的不足.

2 其中鹤城区、洪江市、新化县等地部分年份的数据缺失，所以将其剔除.

3 Levin，Lin & Chut原假设:同质面板单位根；Im，Pesaran & Shin W-stat、ADF - Fisher Chi-square、 PP - Fisher Chi-square的原假设:异质面板单位根；同质面板指所有部门系数相同，异质面板指所有部门系数不相同.

4 Pedroni构造的7个检验面板统计关系的统计量分别为: Panelν、Panelρ、Panel PP、Panel ADF、Group P、 Group PP 和 Group ADF。其中前4个统计量假设不同的截面具有相同的自回归系数，后3个统计量假设不同的截面具有不同的自回归系数.

5 变系数模型假设模型个体成员既有个体影响又有结构变化.

6 这类模型假设所有横截面个体在各个不同时期的斜率和截距都是相同的.

参考文献：

［1］赖娟. 金融发展抑制还是促进了经济增长—来自江西省的数据检验［J］. 江西财经大学学报，2013（02）:17-24.

［2］陆静. 金融发展与经济增长关系的理论与实证研究—基于中国省际面板数据的协整分析［J］. 中国管理科学，2012（01）:177-184.

［3］武志. 金融发展与经济增长:来自中国的经验分析［J］. 金融研究，2010（05）:58-68.

［4］韩廷春. 金融发展与经济增长的内生机制［J］. 清华大学学报，2003（S1）:80-85.

［5］冉光和，李敬，熊德平，温涛.中国金融发展与经济增长关系的区域差异—基于东部和西部面板数据的检验和分析［J］.中国软科学，2006（02）:102-110.

［6］马轶群，史安娜. 金融发展对中国经济增长质量的影响研究—基于VAR模型的实证分析［J］.国际金融研究，2012（11）:30-39.

［7］梅丹，周松. 中国城市金融发展与经济增长关系的实证研究:1990-2005［J］. 经济地理，2008（01）:91-95.

［8］陈伟国，樊士德. 金融发展与城乡收入分配的库兹涅茨效应研究—基于中国省级面板数据的检验［J］. 当代财经，2009（03）:44-49.

［9］李志军，奚君羊. 中国金融发展与收入差距的倒U关系分析［J］.上海经济研究，2012（09）：12-18

［10］刘朝阳，梁惠娟，赖洪婷. 金融发展对居民收入分配的影响研究—基于广东的实证分析［J］.海南金融，2014（02）:21-26.

［11］Clarke George. Xu Lixin Colin and Zou，Heng-fu，2003，Finance and Income Inequality: Test of A ltemative Theories World Bank Policy Research Working PaPer2984，March.

［12］于潇，王学龙，白雪秋. 金融发展对贫富分化抑制作用的研究［J］. 经济研究，2011（06）: 16-24.

［13］温涛，冉光和，熊德平. 中国金融发展与农民收入增长［J］. 经济研究，2005（09）:30-43.

［14］杨俊，李晓羽，张宗益. 中国金融发展水平与居民收入分配的实证分析［J］. 经济科学，2006（02）:23-33.

［15］刘红，叶耀明. 金融集聚与区域经济增长：研究综述［J］. 经济问题探索，2007（11）：46-45.

［16］苟小兰. 我国金融集聚与经济增长的区域差异研究［D］. 西南大学，2014，5，20:47.

［17］C. Kao. Spurious Regression and Residual-based Tests for Cointetration in Panel Data［J］. Journal of Econometrics，1999（90）:1-44.

［18］C. Kao. 2000. NonstationaryPanels，Cointegration in Panels and Dynamic Panels，Advances in Econometrics，Vol.15，No.1:93-130.

［19］P. Pedroni 2004. Panel Cointegretion: Asymptotic and Finite Sample Properties of Pooled Timeseries Tests with an Application to the PPP Hypothesis ［J］.Econometric Theory，Vol.20，No.3:597-625.

［20］江春，张秀丽. 金融发展与企业家精神:基于中国省级面板数据的实证检验［J］. 广东金融学院学报，2010（02）:62-70.

［21］邓永亮. 基于VAR模型的金融发展与经济增长的实证分析［J］.兰州商学院学报，2010（01）:79-86.

［22］张军. 中国的信贷增长为什么对经济增长影响不显著［J］. 学术月刊，2006（07）:69-75.

［23］Kindleberger and Charles P. The Formation of Financial Centters:A Study in Comparative Economic History. Princeton University Press，1974.

（责任编辑：龙 蓉）

Financial Resource Agglomeration and Economic Growth of Hunan Wuling Mountain Area

LIAO Kaicheng，PENG Geng，LIU Fang，WANG Hao
（Business School，Jishou University，Jishou 416000，China）

Abstract：The research on the influence factors of economic growth in poor areas is a hotspot，but there are little literatures discussing that from the perspective of financial resources agglomeration. This paper uses the panel data from 2003 to 2011 of Hunan Wuling Mountain Area and the fixed effect variable coefficients model and Pooled GLS to do empirical research. The results indicate that the relationship between the degree of financial agglomeration and economic growth of Hunan Wuling Mountain Area exists reverse change in the same period，and the influence of regional financial agglomeration degree on economic growth isn’t significant，most of which is negative. From three aspects，this paper analyses the reasons for this phenomenon.

Keywords：Financial Agglomeration； Economic Growth； Fixed Effect Variable Coefficient Model； Pooled Generalized Least Squares Method

中图分类号：F832；F124

文献标识码 ：A DOI∶10.3969/j.issn.1003-8256.2016.02.011

基金项目：湖南省社科基金项目资助（15YBX046）、湖南省教育厅优秀青年项目资助（14B145）、吉首大学大学生研究性学习和创新性实验计划项目资助（201513）

作者简介：廖凯诚（1990-），男，汉族，江西新余人，吉首大学商学院硕士研究生，研究方向为区域金融；彭耿（1979-），男，汉族，湖南邵东人，博士，教授，硕士生导师，研究方向为金融风险管理。