防屈曲支撑性能指标及其工程应用研究

任凤鸣，陈浩帆，郭亚鑫

(广州大学 土木工程学院，广东 广州 510006)

防屈曲支撑性能指标及其工程应用研究

任凤鸣，陈浩帆，郭亚鑫

(广州大学 土木工程学院，广东 广州 510006)

摘要：基于美国规范ASCE41-13中对防屈曲支撑(BRB)性能指标的限值规定，采用大型非线性有限元分析软件ABAQUS，模拟分析了防屈曲支撑在不同性能水准下的受力性能和损伤程度，验证了美国规范性能指标限值的可行性，并结合实际工程实例，研究了防屈曲支撑性能指标对构件性能评估的意义，及其在基于性能的结构抗震设计中的应用.结果表明：有限元计算结果能准确地模拟防屈曲支撑的受力变形状态并验证其性能指标的正确性；该性能指标在基于构件性能的结构抗震评估研究中具有重要意义.

关键词：防屈曲支撑；性能指标；性能水准；工程应用

防屈曲支撑(Buckling-restrained brace，简称BRB)是一种高效的抗侧力构件，它兼具了普通钢支撑和金属耗能阻尼器的双重功能，在小震作用下性能与普通钢支撑相似，能够提高结构的整体抗侧刚度，在中震和大震作用下会率先屈服耗散地震能量，却不易发生屈曲，从而提高结构的抗震性能[1].近40年来，尤其是美国北岭地震和日本神户地震后，防屈曲支撑在日本和美国等国家以及台湾地区得到了较好的应用[2-4].自汶川和玉树地震后，防屈曲支撑因其优越的抗震性能不仅在我国地震多发区的新建框架结构和旧建筑的改造加固中得以应用，而且在新建超高层建筑中的应用也日渐增多，如上海世博中心等[5]超高层建筑均采用了防屈曲支撑作为伸臂桁架.

基于性能的抗震设计理论兴起于上世纪90年代的欧美和日本，并不断得到国内外学者的关注，如今已成为结构抗震设计方法的发展趋势.基于性能的抗震设计研究不仅包括性能目标的确定、实现多性能目标的通用设计方法以及结构整体性能评估，同时也包括对结构构件的变形限值和性能评估的研究[6-9].目前国内外学者已对钢筋混凝土柱、钢筋混凝土梁以及钢筋混凝土剪力墙等构件在破坏过程中的损伤水平进行划分，并用特定的性能指标对其进行量化表达[10-12].随着防屈曲支撑在各种结构中的应用，其基于性能的相关研究也势在必行，但目前针对防屈曲支撑构件的研究主要集中于对构件性能的试验研究和计算分析[13-16]，对其性能指标限值及其在工程中的应用研究还较少[7]，因此笔者将对防屈曲支撑的性能指标展开研究，并结合工程实例论述其在实际工程中的应用.

1防屈曲支撑的性能指标选取

图1　力—位移模型图Fig.1　Diagram of force-deformation

防屈曲支撑通常为轴向受力，其破坏形态以轴向变形破坏为主，因此选取塑性轴向变形作为衡量构件损伤水平的性能指标.根据已有的防屈曲支撑构件拟静力试验为基础，采用通用有限元软件ABAQUS进行建模分析，验证其性能指标限值的合理性.

2有限元数值分析

2.1有限元模型的建立

以文献[15]中的试件QYF 245×2300-A1为模型建立有限元模型，采用三维实体建模，真实地反映防屈曲支撑的性能特点.核心单元和外约束单元均采用8节点六面体减缩积分单元(C3D8R)进行模拟，建立的防屈曲支撑有限元模型如图2所示.

图2　防屈曲支撑有限元模型Fig.2　Finite element model of BRB

核心钢材的本构关系采用Chaboche[17]提出的钢材本构关系(Combined)，强化法为混合强化法则，即等向强化和随动强化的结合.结合实际受力状态，外部约束中的钢材和混凝土的本构关系均设置为弹性本构模型.芯材与混凝土的接触面法向作用采用“硬接触”(Hard contact)，不考虑两者之间的摩擦作用，选择有限滑动滑移公式；外部约束中的钢管与混凝土的相互作用则采用“绑定”(Tie)关系.根据试验中采用的加载机制，以构件的总长度L为基准，依次在L/1 000，L/500，L/300，L/200，L/150等位移幅值下进行往复循环加载.

2.2模型验证

图3为有限元模拟结果与试验结果[15]的力—位移曲线对比图.从3(a)中可以看出：有限元计算结果与试验结果的滞回曲线和骨架曲线均吻合较好，滞回环面积总体相差在5%以内.从图3(b)中可以看出：骨架曲线的形状基本为双折线模型，选取曲线中的转折点处位移作为防屈曲支撑的屈服位移.从表1可以得出：防屈曲支撑正向受拉时，屈服荷载误差为6.78%，屈服位移误差为4.1%.通常BRB在试验受压过程中，由于受到约束单元的限制，受压承载力相对受拉时会有所提高，体现出“拉压不等”的特点，与有限元模拟结果的理想状态稍有出入，但误差在允许范围内，证明采用的建模方法和参数设置是合理可行的.

图3　试验与模拟结果对比Fig.3　Results comparison between experiment and simulation

屈服荷载/kN试验值模拟值屈服位移/mm试验值模拟值301.68281.242.212.12

2.3构件损伤程度分析

由数值分析结果可知：Δy=2.12 mm，则IO，LS，CP三个水准对应的BRB轴向位移(包括屈服位移)分别为8.48，23.32，30.32 mm.对BRB进行以上三个位移幅值下往复拉压的数值模拟，BRB在各水准下的应变如图4所示.

图4　各性能水准下的轴向应变Fig.4　Strain distribution at different performance level

有限元计算结果表明：3个位移限值下BRB芯材的受力较为均匀，并出现了不同程度的塑性损伤.IO水准下BRB芯材的应力略微超过屈服强度270 MPa，对应的应变约为0.7%，进入塑性程度较轻，损伤并不明显，仅能耗散非常少量的能量；LS水准下BRB芯材的应力已接近390 MPa，对应的应变约为1.7%，可见塑性损伤程度相对于OP水准时有较大的发展.CP水准下BRB芯材的应力较LS水准下的应力增加不多，但应变的增大明显，芯材应变达到了2.3%，防屈曲支撑进入塑性程度较深.程光煜等[18]研究表明：当BRB屈服段应变小于3%时，能够保持稳定的力学性能，因此三个性能水准下BRB性能指标的限值是较为合理的.

在反复荷载作用下，一个滞回环所包围的面积表示构件在一次加载中所消耗掉的能量.耗能系数E是指一个振动周期内能量耗散量与振幅最大处所在具有的弹性势能的比值，又称为能量耗散系数或能量耗散比，其表达式[19]为

(1)

设计中常用的另一系数为等效粘滞阻尼系数ξeq，其计算表达式为

(2)

其中：SABC，SCDA分别为曲面ABC和CDA的面积；SOBE，SODF分别为三角形OBE和ODF的面积.

图5　滞回环示意图Fig.5　Diagram of typical hysteretic loop

由有限元数值分析结果得到的不同性能水准下滞回曲线见图6，耗能系数和等效阻尼比计算结果如表2所示.

从表2可以看出：相比于LS和CP水准，IO水准下的耗能系数和等效阻尼比明显小于二者.耗能系数反映了弹性势能在一个周期内的比例关系，该值较小则说明IO水准下构件刚进入耗能阶段，塑性耗能较少，BRB基本处于轻微塑性受力状态.LS和CP水准下的耗能系数和等效阻尼比基本相等，等效阻尼比达到0.50左右，说明从LS到CP，BRB的强度和刚度均未有较大变化，可以认为LS水准下构件已进入稳定耗能阶段，耗能能力良好.

图6　防屈曲支撑的滞回曲线Fig.6　Diagram of hysteretic loops

性能水准IOLSCPE2.393.053.15ξeq0.380.490.50

综上所述，从应力、应变以及能量耗散等方面对防屈曲支撑在三个不同水准下的构件损伤和耗能情况进行分析可以得出：在IO水准下，构件处于初始耗能状态，构件刚进入塑性阶段，开始产生滞回变形，仅耗散少量能量；在LS水准下，构件处于正常耗能状态，构件进入深度塑性阶段，滞回耗能稳定；在CP水准下，构件处于极限耗能状态，构件轴向变形较大，接近极限位移，但基本能保持稳定耗能的状态.

3实际工程应用

3.1工程概况

某五层现浇钢筋混凝土框架，建筑面积为7 780 m2，结构总高度为23.4 m.抗震设防烈度为8度，设计基本地震加速度为0.2 m/s2，设计地震分组为第一组，场地类别为III类，场地特征周期0.45 s，设计使用年限为50年，建筑抗震设防分类为乙类，房屋抗震等级二级.根据该建筑的结构布置和使用功能，在结构中布置了32个BRB，均采用斜撑式布置，其设置位置见图7，其中画圈位置为BRB设置位置.防屈曲支撑设计参数见表3.

图7　防屈曲支撑平面布置Fig.7　Plane layout of BRB

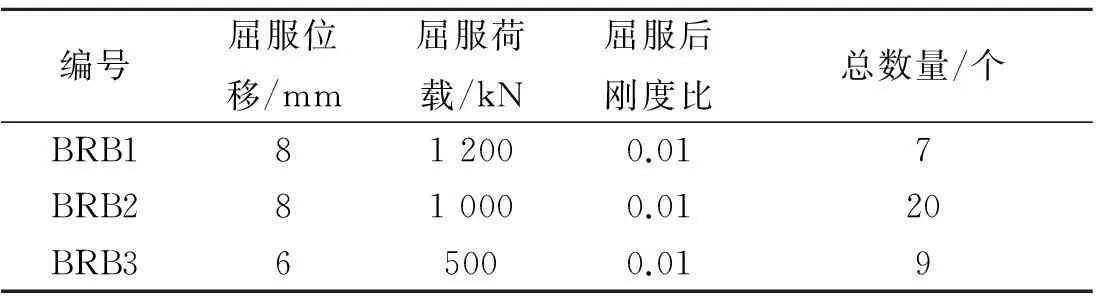
编号屈服位移/mm屈服荷载/kN屈服后刚度比总数量/个BRB1812000.017BRB2810000.0120BRB365000.019

3.2模型的建立与验证

采用PERFORM-3D建立三维有限元模型，如图8所示.钢筋混凝土柱采用纤维单元，钢筋混凝土梁采用塑性铰单元，基础为固结，不考虑土-结构的相互作用的影响.结合原方案SATWE模型信息，建立结构的非线性分析模型.将PERFORM-3D和SATWE模型计算得到的质量对比误差在1%以内，周期对比误差见表4.

图8　PERFORM-3D模型图Fig.8　Diagram of PERFORM-3D model

阶数周期/sSATWEPERFORM-3D误差/%10.95380.98903.6920.86930.91325.0530.77350.80964.67

由表4，5可以看出：原结构PERFORM-3D模型与SATWE模型的结构质量相差很小，前三阶振型的自振周期误差均在5%左右，因此建立的PERFORM-3D模型是相对准确的，能够真实地反映结构性能.

3.3构件性能评估

为了考察该结构中防屈曲支撑在不同水准下的性能情况，利用人工波生成软件生成一条与规范反应谱一致的人工波进行分析，峰值归一化后如图9所示.在罕遇地震弹塑性时程分析中将地震动峰值加速度(PGA)调幅至8度罕遇地震水平，即0.4 m/s2.

图9　人工波Fig.9　Artificial seismic wave

分别对分析模型进行小震、中震和罕遇地震下的动力弹塑性时程分析，根据上述的性能指标限制设置相关参数，计算结果显示：小震下结构中BRB并未出现屈服情况，由此认为BRB的变形满足“小震不屈服”的性能目标.中震下已有部分BRB进入屈服状态，表明RBR在中震下已开始耗能，吸收部分地震能量.而在大震下结构中超过80%的BRB构件已达到屈服状态，部分BRB构件接近IO水准下的变形性能指标，具体比例可见表5(BRB接近OP状态指其轴向位移达到限值的70%).因此，本工程的BRB布置基本满足“中震屈服”的设防目标.通过性能指标的设定，构件在小震、中震和罕遇地震等不同水准下的耗能能力及损伤程度一目了然，满足性能设计要求，证明BRB的性能指标限制是合理的，可以应用于基于性能的结构抗震设计中.

表5罕遇地震下BRB的性能状态分布统计

Table 5Statistic distribution of performance of BRB under rare earthquake

%

从上述分析可以得出：防屈曲支撑的性能指标设定可与性能化设计结合应用，通过对防屈曲支撑位移的数值模拟监测，对实际工程的性能状态进行较为直观而准确的评估，同时结合已有钢筋混凝土结构中梁柱构件的性能指标研究，可对带防屈曲支撑的框架结构体系的整体结构性能进行更为全面的性能评估.

4结论

基于美国规范ASCE 41-13，结合防屈曲支撑拟静力试验以及有限元数值模拟，分析了防屈曲支撑在不同性能水准下的损伤程度及其对应的性能指标限值，建立了构件损伤程度与轴向位移的联系，并验证了其性能指标限值的合理性.结合实际工程，通过对塑性位移这一量化性能指标，较为直观地评估了防屈曲支撑构件在不同地震水准下的性能状态，为既有和新建工程中防屈曲支撑的性能评估和设置防屈曲支撑的结构体系性能分析提供参考.

参考文献：

[1]周云.防屈曲耗能支撑结构设计与应用[M].北京：中国建筑工业出版社,2007.

[2]XIE Q. State-of-the-art of buckling-restrained braces in Asia [J]. Journal of construction steel research,2005，61(6):727-748.

[3]蔡克铨,翁崇兴.双钢管型挫屈束制消能支撑之耐震行为与应用研究[R].台湾：台湾大学地震工程研究中心,2002.

[4]汪家铭,中岛正爱.屈曲约束支撑体系的应用与研究进展(Ⅰ)[J].建筑钢结构进展，2005，7(1):1-12.

[5]武莲霞,余志伟,孙飞飞.屈曲约束支撑在带伸臂高层建筑中的应用[J].建筑结构，2011，41(S1):120-124.

[6]Federal Emergency Management Agency. Prestandard and commentary for the seismic rehabilitation of buildings: FEMA 356 [S]. Reston, VA：American Society of Civil Engineers,2000.

[7]American Society of Civil Engineers. Seismic evaluation and retrofit of existing buildings: ASCE/SEI41-13[S]. Reston,VA: American Society of Civil Engineers，2014.

[8]汪梦甫,周锡元.基于性能的建筑结构抗震设计[J].建筑结构，2003，33(3):59-61.

[9]戴金华,韩小雷,林生逸.基于性能的钢筋混凝土建筑结构抗震设计方法[J].土木工程学报，2011，44(5):1-5.

[10]戚永乐,韩小雷,周新显.钢筋混凝土梁变形指标限值研究[J].建筑结构学报，2014，35(4):185-191.

[11]钱稼茹,冯宝锐.钢筋混凝土柱弯矩-转角骨架线特征点及性能点转角研究[J].建筑结构学报，2014，35(11):10-19.

[12]劳晓春,韩小雷.延性RC剪力墙构件的性能指标限值[J].建筑结构学报，2011，28(9):157-164.

[13]周云,邓雪松,钱洪涛，等.开孔式三重钢管防屈曲耗能支撑性能试验研究[J].土木工程学报，2010，43(9):77-87.

[14]赵俊贤,吴斌,欧进萍.新型全钢防屈曲支撑的拟静力滞回性能试验[J].土木工程学报，2010，44(4):60-70.

[15]赵湘璧.国标Q235一字形防屈曲支撑耗能性能试验研究[D].西安：西安建筑科技大学，2013.

[16]PARK J, LEE J, KIM J. Cyclic test of buckling restrained braces composed of square steel rods and steel tube[J]. Steel and composite structures,2013,13(5):423-436.

[17]CHABOCHE J L. Time-independent constitutive theories for cyclic plasticity[J].International journal of plasticity 1986,2(2):149-188.

[18]程光煜,叶列平,许秀珍，等.防屈曲耗能钢支撑的试验研究[J].建筑结构学报,2008，29(1):31-39.

[19]中国建筑科学研究院.建筑抗震试验方法规程：JGJ 101—1996[S].北京：中国建筑工业出版社，1997.

(责任编辑：刘岩)

Research on performance index of BRB and its engineering application

REN Fengming, CHEN Haofan, GUO Yaxin

(College of Civil Engineering, Guangzhou University, Guangzhou 510006, China)

Abstract:Based on the limits of the performance index of buckling-restrained braces (BRBs) in the American code (ASCE41-13), a numerical study is carried out with the nonlinear finite element analysis software ABAQUS to investigate the mechanical performance and damage degree of BRBs at different performance levels and to verify the limits of the performance index in the American code. Combined with engineering examples, the significance of the performance evaluation of structural members is studied and the application in the performance-based seismic design is discussed. It is shown that the results of finite element computations can accurately model the forces and deformations of BRBs and verify the validity of the performance index. The performance index is of important significance for the structural seismic evaluation based on the performance of components.

Keywords:buckling-restrained brace (BRB); performance index; performance level; engineering application

收稿日期：2015-11-13

基金项目：国家自然科学基金资助项目(51578165，51278130)

作者简介：任凤鸣(1975—)，女，陕西凤翔人，副教授，博士，主要从事组合结构和耗能减震结构的抗震性能研究，E-mail：rfm@gzhu.edu.cn.

中图分类号：TU352

文献标志码：A

文章编号：1006-4303(2016)03-0305-05