大数据下图三角计算的研究进展

金宏桥，董一鸿

（宁波大学信息科学与工程学院，浙江 宁波 315211）

综述

大数据下图三角计算的研究进展

金宏桥，董一鸿

（宁波大学信息科学与工程学院，浙江 宁波 315211）

图三角数量的计算是计算网络聚集系数和传递性的重要步骤，广泛应用于重要角色识别、垃圾邮件检测、社区发现、生物检测等。 在大数据背景下，计算图中三角形算法主要面临时空消耗和计算准确性两大难题。介绍了代表性的大图中计算三角形的算法，主要存在准确计算和近似计算两大类。 准确计算算法又分为内存算法、外存算法和分布式算法，时空消耗或 I／O 消耗很大。 近似计算算法中，有辅助算法、非流式算法和流式算法之分。最后对计算三角形算法进行了归纳总结。

准确计算；近似计算；三角形；图

1 引言

随着网络技术和社会网络服务的发展，网络中的数据量和信息量越来越大。在这种大数据的环境下，对数据的分析和挖掘显得尤为重要。近年来，对有大规模数据的网络的分析得到越来越多的关注。计算机学科的数据结构图可以作为很多种网络的模型，如万维网、P2P 网络和社交网络等都可以用含有特定信息的图作为它们的模型。对网络的分析逐渐转化为对保存网络重要信息的图的分析。由于网络中的关系和个体数量非常多，所以作为其模型的图的规模也很大。

社会网络的同质性和传递性产生了对图中三角形的研究。图中的三角形是复杂网络分析的重要角色，不论是来自社会交互、计算机交流、金融交易、蛋白质还是生态学网络，其中三角形的数量都是巨大的，它在这些领域中有着非常广泛的应用。通过三角形的分布可以区分哪些是垃圾邮件的主人。角色行为识别中，通过使用者参与的三角形的数量可以判断这个使用者的地位。生物信息学中的主题检测需要计算三元组的频率。三角形巨大的数量可以与蛋白质交互网络的拓扑结构和功能性相联系。三角形各点度数之间的关系也可以作为基础图的描述符，在数据库中，三角形也有具体的应用。

目 前 图 中 三 角 形 的 计 算 主 要 分 为 准 确 计 算 （exact counting）和 近 似 计 算 （approximate counting）两 种 类 型 。准确计算可以准确地计算图中三角形的数量，对于大图来说，规模很大，所以计算的时空消耗很大，外存算法的I／O 消耗也 会很大 。研 究人员 的重点就是 在保持准确计算的情况下，减少时空消耗和 I／O 次数。近年来，分 布式框架 MapReduce 的出现，也使很多研究人员研究此框架下的计算三角形算法。相较而言，近似计算比准确计算的实际应用更广泛，同时空间消耗较少。在保持一定准确度的情况下，研究人员对近似计算三角形数量更感兴趣。对于近似计算，大部分的研究者将重点放在采样上，通过一定的采样方法证实，采样得到的三角形数量与实际数量的差值很小，同时将时间空间的复杂度降低。目前，采样方法很多，各有所长。准确计算三角形算法的部分关键点也可以用在近似计算算法上。如上文所述，随着互联网的快速发展，大规模的图不断涌现，在图流中使用限制的内存来估算三角形的数量，这个问题的研究意义越来越显著，同时难度也越来越大。

2 图三角的基本概念

定 义 1 （三 角 形 ）给 定 一 个 图 G=（V，E），它 包 含 了 一个 顶 点 集 合 V、一个边的 集 合 E，|V|和|E|分 别 表 示 顶 点 和边 的 个 数 。如 果 顶 点 u、υ、w∈V ，边｛u，υ｝、｛υ，w｝、｛w，u｝∈E，那 么 3 个 顶 点 和 3 条 边 组 成 一 个 三 角 形 ，称为 ∆uυw。

定义 2 （三角形的实际数量、准确数量和估算数量）用 T 表示图 G 中三角形的实际数量，用 t表示通过准确算法得出的图 G 中三角形的数量，用 T＇表示通过估计算法得出的图G中三角形的数量。

定 义 3 （度 和 邻 域 ）顶 点 υ的 邻 域 Γ（υ）表 示 所 有 与顶 点 υ相 邻 的 点 ，满 足 Γ（υ）=｛u∈V：（u，υ）∈E｝。顶 点 υ的 度 d（υ）是顶点 υ连 接 的 所 有 边 的 个 数或 者 是 它 的 邻 域 ，满 足d（υ）=|Γ（υ）|。图 G 最 大 的 度 dmax（G）是指图中顶点最大的度，即 dmax（G）=max｛d（υ）：υ∈V｝。 m、n 分 别 表 示 图 中 边 、点 的 个数，顶点的度和图中的边数满足。入度和出度是对于有向图来说的，一个顶点的入度等于被所有箭头所指的数量，一个顶点的出度等于被所有箭尾所指的数量。

定 义 4 （（1+ε）-approximation） 返 回 q 的 以 ε为 因 子的估计值 q＇，当 q 满足（1-ε）q≤q＇≤（1+ε）q，其中，ε＜0。

定义 5 （（ε，δ）-approximation）返 回 q 的 以 ε、δ为 因 子的估计值 q＇，当 q 至少以 1-δ的可能性满足，（1-ε）q≤q＇≤（1+ε）q，其中，ε＜0，δ＜1。

定义 6 （图流）图中的边是以一串流的形式加入的。

3 图三角的准确计算

图三角的计算有准确计算和近似计算两种类型。准确计算图三角算法目前有内存算法、外存算法、分布式算法 3 类。内存算法指当内存能容纳整个图，可以在内存中将图中的三角形计算出来的算法；外存算法是指当图的规模很大，不能全部存入内存进行计算时，通过一定的策略将图分为几个部分存入内存进行计算，这种算法会产生一定数量的 I／O 操作；分布式算法是指用分布式框架来计算图中三角形数量，目前主要采用 MapReduce 框架。内存算法中除了具有代表性的Node-iterator［1］和 Edge-iterator算法，还有 Matrix-multiplication［2］算法。基于点边迭代和矩阵相乘也出现了一系列改进的算法 ，有 AYZ［3］、Node-iterator-core［4］、Forward［5］、Forward-hashed［6］、Compact-forward［7］。 时 隔 多 年 又 出 现 了 结 合 点 边 迭 代 的Combined Iterator［8］算 法 。本 文 将 介 绍 两 个 外 存 算 法 ：Chu 和Cheng［9］提 出 的 基 于 图 划 分 的 算 法 和 Hu［10］提 出 的 有 效 I／O的算法。近些年来，随着分布式框架的应用，出现了基于MapReduce 框 架 的 GP［11］、TTP［12］以 及 CTTP［13］算 法 。目 前 出现的准确计算图三角算法都应用在静态图上。以下将一一介绍。

3.1 内存算法

内存算法最初适用于规模比较小的图，小图完全可以存入计算机内存中，并进行计算。内存算法最先找到了如何使用计算机解决三角形计算问题的方法，并且不断地在算法细节中得到突破，以减少运行时空成本。其中，基本迭代算法简单，但成本高，不适合规模大的图。Fast Common Neighbor Iteration 算 法 通 过 混 合 线 性 扫 描 二 分 法 和 分 段 索引法，在时间上进行了很大优化，同时增加了空间的开销。随着图规模的增长，内存算法需要更大内存的计算机。

3.1.1 迭代算法

Node-iterator（点 迭 代 ）算 法 检 测 每 一 个 顶 点 的 每 一 对邻点之间是否有一条边，如果有，那么就得到一个三角形，反之得不到。为了使每一个三角形只被计算一次，需要安排 每 个 顶 点 的 顺 序 。Edge-iterator（边 迭 代 ）算 法 迭 代 所 有边，比较每条 边 两个顶点 的 领域，对于一条 边｛u，w｝，仅当 υ同时出现在 Γ（u）和 Γ（w）中，3 点｛u，υ，w｝才组成一个三角形。

Alon、Yuster 和 Zwick 将 点 迭 代 和 矩 阵 相 乘 结 合 在 一起，得到 AYZ 算法。算法将点集分为度数低的顶点集合Vlow=｛υ∈V：d（υ）≤β｝和 度 数 高 的 顶 点 集 合 Vhigh=V／Vlow，其 中 ，β=mγ-1／γ+1，γ 是 矩 阵 乘 法 指 数 。低 度 数 的 点 集 采 用 标 准 点 迭代方法，高 度 数 点 集 采 用 快 速 矩 阵 乘 法 。Node-iterator-core算法是在点迭代的基础上，在每次选择顶点迭代时选择当前度数最小的顶点，当此顶点所在的三角形全部被计算后，将此顶点删除。Forward 算法是边迭代算法的改进。在边迭代算法中，需要将边两个顶点的所有邻接顶点都比较一下，在 Forward 算法中只需要比较边迭代中所有邻接顶点的子集 A。在这个算法中，由于所有的点都是有顺序的，所以 可以将图 视 为有向图 ，方 便 理 解算法过 程 。A（υ）的 数据结构的大小是不大于点 υ的入度。Latapy M 提 出 了 一 个对 Forward 改 进 的 算 法 Compact-forward。Compact-forward使用迭代器迭代邻接点的子集，迭代方法和边迭代方法相同。邻接点是排序过的，比较语句也在一个可达的确定指数前停止。虽然时间上界和 Forward 算法相同，但是它不需要额外的数组，因此节省了时间和空间。

Oracle Labs 的 Sevenich M 提 出 了 FCNI （fast common neighbor iteration）算 法 。该算法的基准算法是结合点迭代、边迭代两种迭代算法的 Combined Iterator算 法 ，该 基 准 与前面 提 到 的 Forward 算法类 似 ，多了邻点 选择 时 的 排 序。FCNI 算 法 指 出 Combined Iterator 算 法 的 主 要 部 分 是 重 复求出不同顶点对的共同邻点，所以想要快速计算三角形的个数，就需要快速求出顶点对的共同邻点。面临的问题是：求一个度很高的顶点和其他顶点的共同邻点需要很长的时间。于是他们提出了两个方法来解决这个问题：混合线性扫描二分法和分段索引法。每个顶点的邻点存储在有序的邻接数组中，问题转化为求两个有序数组的共有元素。当两个数组长度差距过大时，采用二分法，算法从选择长数组的中间元素和用二分查找短数组开始。当两个数组度都较小时，采用线性扫描。算法又将度数高的顶点构建了索引，对他们的邻点数组构造了分段索引。这两个方法的应用使该算法的运行时间大大减少，在当前内存算法中运行时间最少。

3.1.2 矩阵相乘算法

在 矩 阵 相 乘 （matrix-multiplication）算 法 中 ，假 设 A 是图 G 的邻接矩阵，A3对角线上的数字分别代表对应顶点所在三角形个数的两倍。A3对角线上的数字之和代表图 G中三角形个数的 6 倍，因为三角形由 3 个顶点组成，一个三角形会被重复计算 3×2 次。这会导致算法运行时间达到O（n3）。通过快速矩阵相乘的方法可以使运行时间下降。

3.2 外存算法

当图的规模过大或者计算机的内存不足以装下整个图时，采用外存算法是基本策略。外存算法需要解决的问 题是保证计算 的三角形个数的 准 确性，同时减 少 I／O 操作。Chu、Cheng 算法和 MGT 算法都是将图的信息分段载入内存进行计算。 不同的是，分别用不同的方法保证图中三角形不被拆开。前者划分子图时保留了所有顶点的邻点，后者在有向化图之后载入子图和顶点的邻接表。表 1 是在 I／O 操 作 和 运 行 时 间 方 面 ，对 Chu、Cheng 算 法 DGP、RGP 和算法 MGT 在内存使用率为 25%时，各算法在不同数 据 集 上 的 效 果 比 较 ，其 中 ，使 用 的 机 器 是 3 GHz CPU 和8 GB 的 内 存 。MGT 算 法 在 I／O 操 作 数 和 运 行 时 间 上 都 优于 Chu、Cheng 算法。

表1 DGP、RGP 和 MGT 的比较

3.2.1 基于图划分的算法

Chu 和 Cheng 提 出 了 基 于 图 划 分 的 外 存 图 三 角 计 算算法，该算法首先将整个图划分成几个子图后，存在外存，子图的规模小，就可以放入内存。 然后依次将每个子图调入内存，计算当前子图中的三角形数量。为了保证图划分后不会将三角形拆开，每个子图实际上也保留了当前部分中所有顶点的邻点，如图 1、图 2 所示。 根据划分图的方法 ，Chu 和 Cheng 有 两 种 方 法 ：DGP （deterministic graph partition）和 RGP（randomized graph partitioning）。 前 者 采 用确定方法划分子图，后者采用随机方法划分子图。 划分子图是一个难题，如果某部分子图的邻点很多，会使算法的时空效率变高。

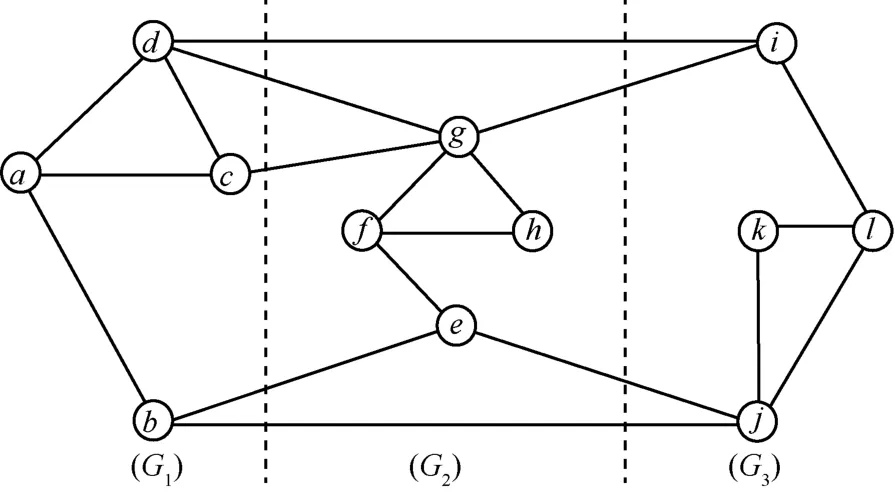
图1 基于图划分算法的原图

3.2.2 有效 I／O 算法

Hu X C 和 Tao Y F 设 计 了 一 种 有 效 I／O 算 法 ，计 算 三角 形 算 法 MGT（massive graph triangulation），这 是 针 对 静 态的图。这个算法与 Chu 的算法有明确的不同。他们将无向图以有向图的形式表现出来，如图 3所示。有向图的有向边是根据无向图顶点的度和编号设置指向的。例如，当顶点 a的度小于 b的度或者 a的度等于 b的度但 a的编号小于 b 的 编号，定义 a＜b，此时 无 向边｛a，b｝在 有 向 化后 是 a 指 向 b。无 向 三 角 形 ∆uυw变 为 有 向 三 角 形，当 u＜υ＜ w，其 中 ，顶 点 u 被 称 为 （cone vertex 锥 顶 点 ），边 ｛υ，w｝被 称为（pivot edge 中枢边），如图 4 所示。 算 法 的 准 备 工 作 是 将无向图根据规则进行有向化，并以邻接表的形式存储，每一个顶点的邻接表只存它的出—邻居（即它指向的顶点）。MGT算法是逐步将有向图中的边载入内存，根据需要从外存载入关联的顶点，计算出三角形的数量。具体过程是：

·将有向图中的一部分边载入内存；

·得出当前内存中的边所在的顶点；

· 对于每一个顶点 υ，从外存中得到它的邻接表（出—邻接表），将其出—邻居与内存中的顶点做交集。 将顶点υ到交集得到的顶点所成的边与当前载入内存中的有向图的边做并集，找出其中以 u为锥顶点的三角形个数，并释放相应的空间。

MGT 算法可以正确地找出所有的三角形，因为第一步保证了每一条有向图的边都可以在一个独特的迭代中载入内存。同时第二步保证了可以找出以当前载入内存的边为中枢边的三角形。MGT 算法在 I／O 和 CPU 上都非常高效。

图2 基于图划分算法划分后的图

图3 无向图变为有向图

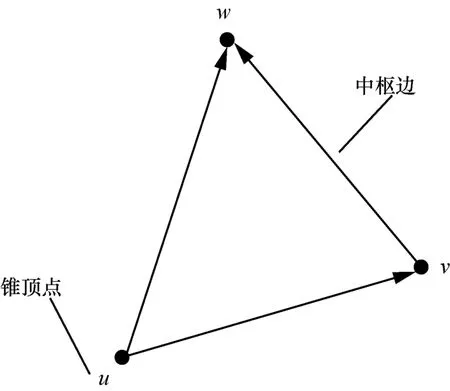
图4 有向三角形

3.3 分布式算法

由于分布式算法的普及，一些研究使用 MapReduce算法计算图三角。目前使用 MapReduce 框架的算法是基于图划分来分析问题的。在某些方面加快了计算算法，但同时也出现了一些问题。接下来介绍 3种基于MapReduce 框架的算法。这 3 个算法有一个共同的基础，是图的分割。图的分割算法是先将顶点均分为p个部分（partition），V=V1∪V2∪ … ∪Vp，其 中 ，当 i≠j 时 ，Vi∩Vj=Φ 。 同 时 定 义 Vijk=Vi∪ Vj∪ Vk，Eijk= ｛（u，w ）∈ E ：u，w ∈Vijk｝，Gijk= （Vijk，Eijk）。Gijk叫 做 3-partition ，Gij是 2-partition ，Gi是 1-partition ，Gijk和 Gij的 含 义 如 图 5 、图 6 、图 7 所 示 。GP算法是 三 角 形 计 算 在 MapReduce 上 的 初 次 应 用 ，GP 算法有很多冗余计算。TTP 算法发现 GP 算法有很多冗余计算，原因是在 map 阶段输出了重复的边。为了避免GP 算法冗余计算的产生，TTP 算法定义了 3 个 类型的三 角 形 。CTTP （colored triangle type partition ）算 法 是 针 对GP 算 法 的 “curse of the last reducer”而 被 提 出 的 ，避 免了 不 均 衡 。表 2 是 在 时 间 和 每 轮 MapReduce 中 数 据 shuffle大 小 上 ，对 GP、TTP、CTTP 算 法 的 比 较 。运 行 平 台 是Hadoop，集群由 40 台机器组成 ，每台机器的内存为 4 GB。由表 2 可见，CTTP 算法在时间和空间上都优于GP、TTP算法。

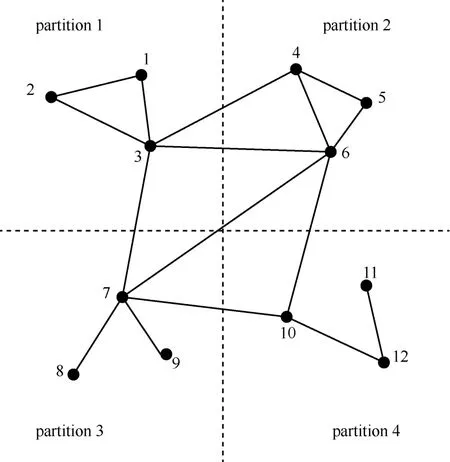
图5 顶 点 平 均 分 为 p 个 部 分 （p=4 ）

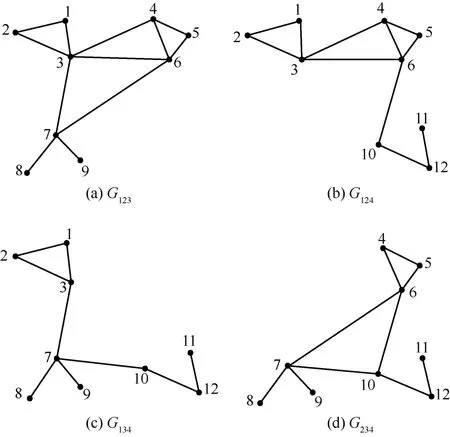
图6 3-partition Gijk

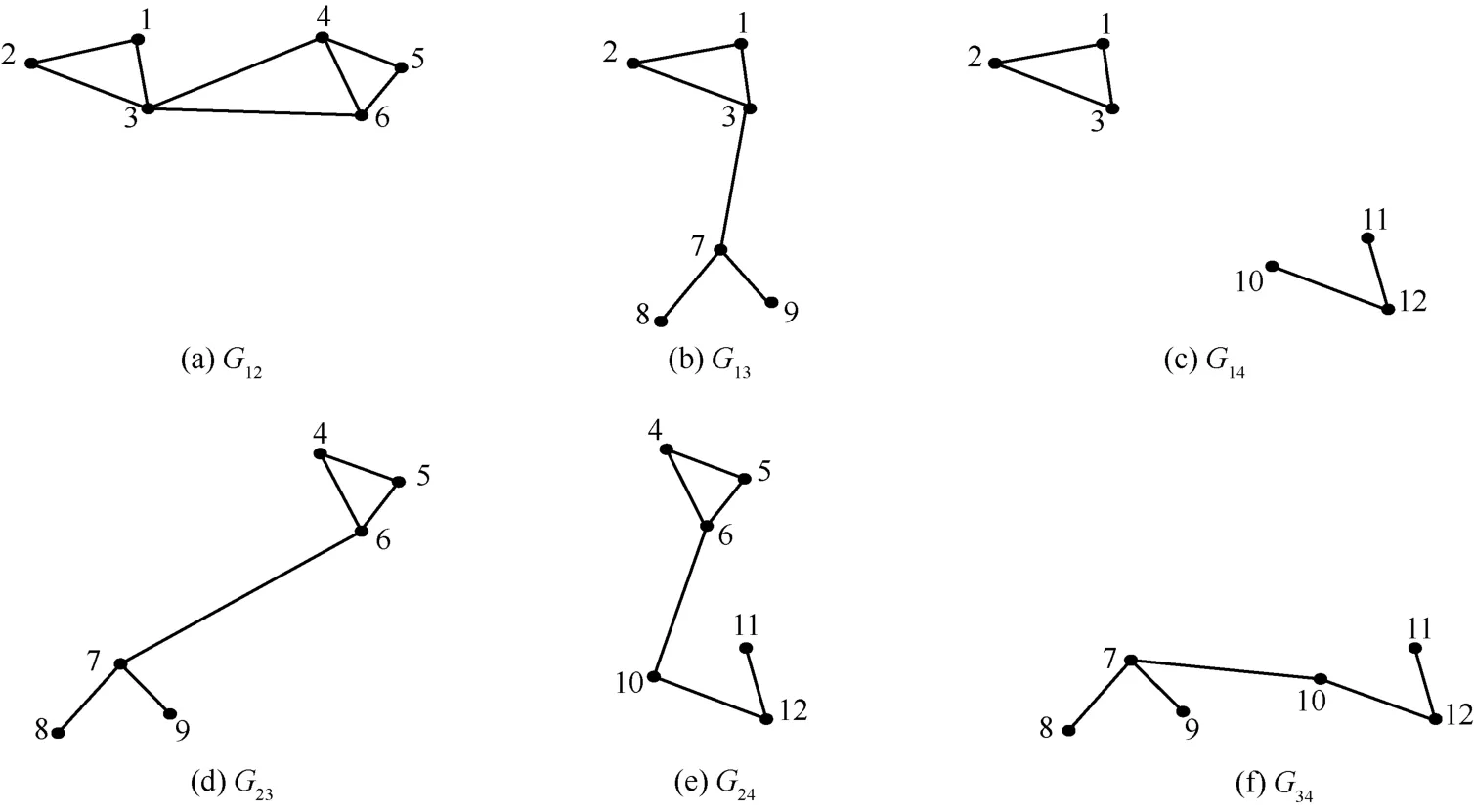
图7 2-partition Gij

表2 GP、TTP、CTTP 算法的比较

3.3.1 GP 算法

Suri 和 Vassilvitskii 使 用 MapReduce 框 架 提 出 了 GP（graph partition）算 法 。算法的第一步是将图中的顶点划分为 p 个 部 分 ，Gi=（Vi，Ei），其 中 ，0＜i≤p，所 以 每 个 部 分 含 有 几乎相同数目的顶点。GP算法使用内存算法计算每一个3-partition Gijk中 三 角 形 的 数 目 ，其 中 ，0＜i＜j＜k≤p。最 后 根据三角形的顶点是否被分到同一个部分，将结果整合起来，得出最终的结果。如果三角形的 3个顶点都出现在同一 个 部 分 中 ，那 么 对 于 3-partition Gijk，此 三 角 形 便 被 计 算了3次。

3.3.2 TTP 算法

Park 和 Chung 针 对 GP 算 法 的 不 足 提 出 了 TTP（triangle type partition）算 法 。Park 和 Chung 认 为 GP 算 法有很多冗余计算，比如上面提到一个三角形可能被计算多次。他们发现三角形被计算多次的原因是，在 map 阶段输出了重复的边。为了避免这个情况的产生，TTP 算法定义了3种类型的三角形。第1类三角形是三角形的3个点在同一个部分中；第2类三角形任意两个顶点在同一个部分中，另一个在其他部分中；第 3 类三角形是指 3 个顶点都在不同的部分中。GP 算法就是重复计算了第 1类和第2 类三角形。TTP 算法为了避免过多的重复计算，定义了 inner-edge：边 的 两 个 顶 点 在 一 个 部分中 ，相 反 的 即 是outer-edge。图 8 表 示 不 含 inner-edge 的 3＇-partition。TTP算 法 在 2-partition 中 计 算 第 1 类 、 第 2 类 三 角 形 ，在3 ＇-partition 中 计 算 第 3 类 三 角 形 ，因 此 减 少 了 冗 余 计 算 ，减少了时间复杂度。

3.3.3 CTTP 算法

Park 和 Silvestri针对 GP 算法的 “curseofthelast reducer”，提 出 了 CTTP（colored triangle type partition）算 法 ，是 第 一 个保 证 了 每 个 reducer 的 最 大 输 入 的 算 法 。该 算 法 是 在MapReduce 的 计 算 模 型 MR（m，M）中 提 出 来 的 ，其 中 ，m 是每个 mapper或者 reducer需要的空间，M 是整个计算中需要的空间。本算法进行 R 次 MapReduce 过程。CTTP 算法从 4-wise 独 立 族 函 数 中 随 机 选 择 一 个 颜 色 函 数 h（·），进 行顶点划分。CTTP 算法在 TTP 算法基础上，将问题分解为子 问 题 。 子 问 题 分 为 两 类 ： 一 类 是 （i， j，k）子 问 题 ，用 来 计 算 第 3 类 三 角 形 ；另 一 类 是（i，j）子 问 题 ，用来计算第 1 类和第 2 类三角形。CTTP 通过均匀地将 K个 子 问 题 分 配 给 R=pE／M round 的 方 法 ，解 决 一 个 子 问 题只需要一个 reducer的问题。如果 R 不是 2 或者 3，那么每一 个 round 解 决 K／R 个 子 问 题 。这 个 算 法 保 证 了 每 一 个mapper发出同样数量的数据对。因此这个算法避免了被一些慢的 mapper延迟了计算。

4 近似计算图三角

由于准确计算图三角的时空复杂度很大，同时很多应用只需要近似得到图三角的数量，所以近年来近似算法得到了很多关注。本文将近似计算图三角算法分为辅助算法、非流式算法和流式算法 3个类别进行介绍。

图8 3＇-partitionGijk＇

4.1 辅助算法

辅助算法是指这类算法经常被其他计算图三角算法引用，常常作为其他算法的一部分。

4.1.1 DOULIN 算法

Tsourakakis C E ，Kang U，Miller G L 和 Faloutsos C发 明 了 DOULIN［14］算 法 。DOULIN 算 法 不 是 处 于 其 他 计 算三角形算法的对立面，而是处于所有算法的友好面。不论图能装进内存还是装不进，它都非常的实用。DOULIN 对每一个边都投掷一枚硬币，此边被保留的可能性是 p，被删除的可能性是 1-p。在最后剩下的图中找到的三角形的个数乘以 1／p3就是对原图三角形个数的估计。

4.1.2 Colorful Function 算法

Colorful Funtion（颜 色 函 数 ）［15］算 法 为 图 中 每 个 顶 点 分配一种颜色 ，总的颜 色数是 N=1／p，其中，p 是一个小于 1的参数。当一个边的两个顶点被分配同一种颜色时，这个边称作是单色的。然后从所有的单色边中采样，计算采样到的单色边组成的三角形的个数，最后将计算的个数 除以 p2，得 出近似估计的三角形个数。这个算法的关键点是关联采样的边。

4.2 静态算法

静态算法是基于静态图的，适用于离线计算。目前近似计算的静态算法只在单机上。在此方向上的研究较少，突破也很少，以下介绍的两种方法是有特点的算法。基于度的顶点划分的算法实现了时间空间更低的复杂度。随机矩阵迹算法采用了蒙特卡洛模拟方法。这两种方法均与其他方法有明显的区别。

4.2.1 基于度的顶点划分算法

Kolountzakis M N［16］等 人 研 究 发 现 ，基 于 度 对 顶 点 进行划分，能得出在计算三角形时更小的运行时间上界。因为每个三角形都对应一个三元组，于是他们构造了一个三元组集合 U，这个三元组集合包括了所有的三角形。在这个集合里，均匀地选出一些三元组，标记为 1 到 s。当第 i个三元组被采样时，如果它是一个三角形，那么 Xi为 1；如果不是，则赋值为 0。由于是均匀地选取，并且一共得出 t＇个 三 角 形 ，那 么 E（Xi）=t＇／|U|。因 为 每 个 Xi都 是 独 立 的 ，所 以通过切诺夫界可以得到：

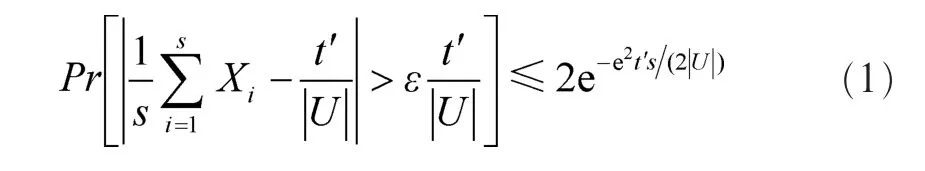
由于|U|≤n3，所 以 运 行 时 间 是 O（n3lgn／（te2））。根 据 度 划分 顶 点 得 出 了|U|更小的上界。理由是：对 于 一 个 包 含 u 的三 元 组 （u，υ，w），如 果 ｛u，υ｝、｛u，w｝∈E，这 些 三 元 组 中 含 有 u的 个 数 最 多 是 d（u）2。 如 果｛υ，w｝∈E，那 么 三 元 组 中 含 有 u的个数最多是 m。当 d（u）2＞m 时，后者的界限更紧。所以，当顶 点 的 度 小 于 m1／2时 ，那 么 它 属 于 低 度 顶 点 ，三 元 组 中 含有 低 度 顶 点 的 三 角 形 的 个 数 最 多 是 m3／2。当 所 有 顶 点 度 之和是 2m 时，三元组中含有高度顶点的三角形的个数最多是 2m3／2。 结 合 起 来 ，|U|的 上 界 是 3m3／2，所 以 得 到 |U|≤O（m3／2），时 间 上 界 是

4.2.2 随机矩阵迹算法

Avron H［17］采 用 随 机 矩 阵 迹 的 方 法 去 估 计 大 图 中 三角形的个数。该方法依据的是准确计算三角形算法里的矩 阵 相 乘 算 法 ，采 用 Monte-Carlo 模 拟 来 估 算 三 角 形 个数 。每 一 个 样 本 需 要 O（E）的 时 间 ，需 要 O（e-2lg（1／δ）ρ（G）2）个 样 本 才 能 保 证 （ε，δ）-approximation，其 中 ，ρ（G）是 对 图 G稀 疏 的 一 种 测 量。这个算法很高效，只需要 O（V）的空间和O（lg2|V|）个 样 本 就 能 达 到 一 个 很 好 的 估 算 。一 个 维 数 高 的矩阵的立方计算量很大，所以这个算法生成一个随机向量x=（xk）， 其 中 ，xi～N（0，1）（ 正 态 分 布 ）。 将 y 赋 值 为 Ax，Ti=（yTAy）／6，循 环 M=|γln2n|次 ，最 后 三 角 形 的 个 数 估 计 为

4.3 流式算法

流式算法基于动态图流，与静态算法相比，适用于在线计算。图流有不同形式，主要分为任意流（arbitrary streams）和事件流（incidence streams）两类。在任意流中，边在流中是不重复的，且是以任意顺序出现的；在事件流中，边是按照每个顶点的邻边出现的，例如，首先顶点 υ1的所有邻点出现，接着 υ2的所有邻点出现。υ1，υ2，…，υn的顺序是由输入方确定的。根据算法通过流的次数，可以将算法又分为 one-pass算法和 multiple-passes 算法。

下 面 介 绍 一 个 multiple-passes 采 样 三 角 形 的 算 法 ，这里 的 流 是 任 意 流 ，算 法 是 Buriol L S［18］提 出 的 3-passes 算法 ：将流中所有边的数目计算出来，为|E|；从 流 中 均 匀 选 择一条边 e=｛a，b｝，也均匀选择出一个顶点 υ，这个顶点属于 V＼｛a，b｝；如果｛a，υ｝和｛b，υ｝都属于 E，计数 β=1，否 则 计 数 β=0。最后 返 回 β值 。这 个 算 法 中 有 一 定 数 目 的 估计器（estimator），每个估计器得到一个 β值，求出期望 E［β］后 ，三 角形的个数 T ＇就 估 算 为 E ［β］·|E|·（|V|-2）／3 。

multiple-passes 算 法 可 以 合 成 为 one-pass 算 法 ，Buriol L S 将 3-passes 算 法 合 成 的 1-pass 算 法 是 ：随 机 取一个顶点 υ，并在流中采样一条边｛a，b｝，如果能在接下来的流 中 检 测 到 边 ｛a，υ｝和 ｛b，υ｝，则 三 角 形 计 数 ，否 则 不 计 数 。multiple-passes 算 法 的 消 耗 多 于 one-pass 算 法［30］。

下面介绍 3 种 one-pass算法：基于邻居采样（Neighborhood sampling）算 法 、基 于 2-path 和 图 稀 疏 的 算 法 和 TRIEST 算法，都与采样有关。但由于采样方法各不相同，3 种算法的时空消耗显而易见。基于 2-path 和图稀疏的算法需要存储多个稀疏图，所以空间消耗很大，TRIEST 算法对每条边的到来都进行一次邻点交集计算，所以时间消耗很大。3种算法的准确率也有差异。表 3是 3个算法准确度的比较。对于几种不同的数据集，并没有完全优势的算法。可见对于含有不同数据意义的应用，需要采用不同的算法。

表3 3种流式算法的准确度比较

4.3.1 基于邻居采样算法

Pavany A 和 Tangwongsan K［19］等 人 设 计 了 一 个 时 间 空间效率都挺高的图流算法。这个算法是基于邻居采样的one-pass算法：首先从流中随机采样一条边，然后采样和该边有共同顶点的边。N（e）表示在流中与边 e 相邻，但是在 e边 后 面 到 来 的 边 。其中，c=c（e）=|N（e）|。 数据以块的形式到达，块的大小是 w。对于每一个边的到来，设置 r个估计器，以 m／（w+m）的概率保留这条边。然后采样边的邻边，以 c+（e）／（c-（e）+ c+（e））的 概 率 从 N（e）∩B 采样一条边。最后判断这两条边能否与后来的边组成一个三角形。这个算法的时间空间复杂度都是 O（r+w）。

4.3.2 基于 2-path 和图稀疏的算法

Bulteau L 和 Froese V［20］等 人 设 计 了 一 个 基 于 2-path采样和图稀疏的方法，来估计动态增删图流中三角形的数量，采用的是 one-pass。相对基础图流采样对删除边后采样的子图是否仍存在的未知，图稀疏能处理边的删除。 该算法 最 大 的 挑 战 是 显示 了 稀 疏 图 中 的 2-path 采样 几 乎 等 同于 原 图 的 2-path 采 样 。 随 机 选 择 了 大 量 的 2-path，与 用 其中能组成三角形的 2-path 数量去估计传递系数。对于图流中 每 一 个 增 删 边 的 到 来 会 更 新 SME （second moment estimator），图流完全通过将返回整体 2-path 值 。与此同时，用 颜 色 散 列 （coloring hash）函 数 族 去 稀 疏 图 流 ，得 到 数 个稀疏图。对于 每一个稀 疏 图 ，随 机采样一 定 数目的 2-path判断是否组成三角形，并计数。最后用稀疏图中采样的2-path 中 能 组 成 三 角 形 的 数 量 与 采 样 的 2-path 数 量 的 比值 ，与 整体 2-path 数 量 比 较 ，去 估 计 整 个图 流 中 三角 形 的数量。该算法得到了图流中计算三角形复杂度的下界。

4.3.3 TRIEST 算法

由于基于采样的流算法，事先都要确定边采样的概率p，所以会造成一些问题。如在存储空间有限的情况下，需要知道流的规模；采样留下的边的规模会增长，如果 p 较大，会溢出存储空间，如果 p 较小，得到的结果是次优的；即使设定了特定的 p，使在流结束时恰好装满存储空间，得到的结果也不是最好的。TRIEST 算法针对这些问题提出了解决方法。

TRIEST［21］算 法 是 在 one-pass 下 的 ，相 对 于 只 有 增 加 边的 流 算 法 MSCOT［22］，它 还 有 删 除 边 的 流 ，时 刻 计 算 三 角 形的数量，并且存储空间是固定的。该算法采用水库采样（reservoir sampling）和 随 机 配 对 （random pairing）两 种 采 样方案使得存储空间尽可能多地被利用。由于是时刻计算三角形的数量，图采用了时间标记 Gt，每到来一条边，时间增长一个单位。该算法默认对一条边的删除一定是在对这条边增加之后。如果设定的内存大小是 M，对于当前流入的插 入 边 e=｛a，b｝，如 果 之 前 图 的 大 小 Gt-1不 大 于 M，当 前 边被保留。如果之前的图的大小已经达到过 M，这时以 M／t的概率决定直接舍弃当前边，或者选择删除之前图中的一条边，且插入当前边，这是标准水库采样的应用。若插入了当前边，便计算当前边是否组成三角形。对于当前流入的边是删除边，计算当前边是否在之前流入的图中组成三角形，如果组成，便减去相应的数量。为保证存储空间在增加边和删除边的时 候都能 充分利用设 定的内 存，TRIEST 基于随机配对做了补偿策略，删除边需要被未来的插入边补偿 。设 置 了 两 个 计 数 器 din和 dout。如 果 之 前 流 入 图 的 大 小Gt-1已经达到内存大小 M，当 前 边 是 一 条 删 除 边 ，如 果 此 删除 边 仍 在 Gt-1中 ，din加 一 ；如 果 此 删 除 边 之 前 被 替 换 出 去 ，不 在 Gt-1中 ，dout加 一 。 之 后 到 来 的 增 加 边 会 根 据 din和 dout的 值 被 保 留 或 不 被 保 留 。如 果 din、dout之 和 等 于 零 ，增 加 边采 用 标 准 的 水 库 采 样 方 案 。如 果 不 等 于 零 ，便 以 din／（din+dout）的 概 率 保 留 增 加 边 ，如 果 保 留 ，din-1，否 则 dout-1。TRIEST算法在完全动态的图流中做到了无偏、低方差、高质量的估计。并且在有数十亿条边的大图中有更小的平均估计误差。

5 性能比较

综上所述，在计算图三角的算法中，准确计算图三角与近似计算图三角算法有区别也有联系。准确计算中，点边迭代算法和矩阵相乘算法是最基础的算法。但是对于数据量越来越大的图来说，在普通计算机上运行这些算法的时间空间复杂度非常高，并不适用。基于它们的改进算法FCNI提供了快速实现求共同邻点的方法，也使在大规模图中计算三角形的运行时间大大提高，但是实验机器成本很高。外存计算算法很好地解决了图规模过大，普通机器内存不够用的问题。Chu 和 Cheng 提出的基于图划分的算法，一定程度上避免了内存小的问题，但是对于不均匀的图来说，划分是一个难 题。Hu 提出的 有 效 I／O 的算 法 ，巧妙避免了重复计算，时空复杂度为目前最好，且可以移植到不同平台上进行计算。GP、TTP 和 GTTP 采用分布式框架为图三角算法提供了新的平台，提供了更多的内存，又可以并行，使时空复杂度减少。TTP、GTTP 分别针对 GP 的重复计算和冗余等待时间做了改进，在 MapReduce 框架下取得了好的效果。近似计算中，DOULION 算法和颜色函数对采样很有帮助，被很多其他算法运用。静态图的计算图三角算法中，基于度分割和随机矩阵迹是有特点的方法，但是空间消耗都较大、效率不高。部分算法是基于动态图流 的 ，multiple-passes 算 法 时 空 消 耗 大 ，更 多 算 法 采 用 的 是one-pass。近似算法大部分采 用采样 方法，各有 优缺点 。 Pavany A 提出的邻居采样算法的空间效率很高，但是参数过多。Laurent提出的基 于 2-path 和图稀疏 的 算法效果 一般，但首次达到了每边的固定处理时间。TRIEST 算法是目前准确率最高的，且可以在固定内存中时刻计算图流中三角形数量。近似计算应用范围很广，并且较准确计算来说需要的时空复杂度明显降低，但准确度是一个关键问题。大部分近似算法是在准确计算的基础上进行改进的，如矩阵迹算法是在矩阵相乘算法上加入了蒙特卡洛方法。上文几种采样算法是在点边迭代算法的基础上加入了采样策略。

本文将近几年的计算图三角算法按准确计算和近似计算进行了比较，见表 4、表 5。

表4 准确计算三角形算法比较

表5 近似计算三角形算法比较

6 结束语

面对社会网络的快速发展，图的规模越来越大，关于图的问题也越来越多样化。选择合适图存储模型和计算模型对图的计算很重要。根据不同的问题需要选择不同的解决方案，面对新的应用也要研究出新的方法。近年来出现的高效的分布式系统为图三角算法提供了新的平台。基于分布式的三角形计算算法的可行性越来越大，这将会成为三角形计算的下一个研究重点。

［1］ THOMAS S.Algorithmic aspects of triangle-based network analysis［J］.Phd in Computer Science，2007：26-29.

［2］ COPPERSMITH D ，WINOGRAD S.Matrix multiplication viaarithmetic progressions ［J］.Journal of Symbolic Computation，1990，9（3）：251-280.

［3］ ALON N，YUSTER R，ZWICK U.Finding and counting given length cycles［J］.Algorithmica，1997，17（3）：209-223.

［4］ THOMAS S，WAGNER D.Finding，counting and listing all triangles in large graphs，an experimental study ［C］／／The 4th International Workshop，May 10-13，2005，Santorini Island，Greece.New York：Springer，2005.

［5］ CHIBA N，NISHIZEKI T.Arboricity and subgraph listing algorithms［J］.Siam Journal on Computing，1985，14（1）：210-223.

［6］ KUMAR R，RAGHAVAN P，RAJAGOPALAN S，et al.The web as a graph：measurements，models，and methods ［C］／／The 5th Annual International Conference，July 26-28，1999，Tokyo，Japan.New York：ACM Press，2000：1-17.

［7］ LATAP M.Theory and practice of triangle problems in very large （sparse （power-law）） graphs［EB／OL］. ［2006-09-20］.http：／／arxiv.org／pdf／cs／0609116.pdf.

［8］ SEVENICH M，HONG S，WELC A，et al.Fast in-memory triangle listing for large real-world graphs［C］／／The 8th Workshop on Social Network Mining and Analysis SNAKDD，August 24-27，2008，Las Vegas，NV，USA.New York：ACM Press，2014.

［9］ CHU S，CHENG J.Triangle listing in massive networks and its applications ［C］／／The 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining， August 21-24，2011，San Diego，CA，USA.New York：ACM Press，2011：672-680.

［10］HU X C ，TAO Y F.I／O efficient algorithms on triangle listing and counting ［J］.ACM Transactions on Database System，2014，39（4）：1-30.

［11］SURI S，VASSILVITSKII S.Counting triangles and the curse of the last reducer ［C］／／The 20th International Conference on World Wide Web，March 28-April 1，2011，Hyderabad，India.New York：ACM Press，2011：607-614.

［12］PARK H M，CHUNG C W.An efficient MapReduce algorithm for counting triangles in avery large graph ［C］／／ACM Conference of Information and Knowledge Management， October 27-November 1，2013，San Francisco，CA，USA.New York：ACM Press，2013：539-548.

［13］PARK H M，SILVESTRI F，KANG U，et al.MapReduce triangle enumeration with guarantees［C］／／ACM Conference of Information and Knowledge Management，November 3-7，2014，Shanghai，China.New York：ACM Press，2014.

［14］TSOURAKAKIS C E，KANG U，MILLER G L，et al.DOULIN：counting triangles in massive graphs with acoin ［C］／／The 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining，June 28-July 1，2009，Paris，France.New York：ACM Press，2009：837-846.

［15］PAGH R，TSOURAKAKIS C E.Colorful triangle counting and Mapreduce implementation ［J］.Information Processing Letters，2011，112（7）：277-281.

［16］KOLOUNTZAKIS M N，MILLER G L，PENG R，et al.Efficient triangle counting in large graphsvia degree-based vertex partitioning［J］.Internet Mathematics，2010，8（1-2）：15-24.

［17］AVRON H.Counting triangles in large graphs using randomized matrix trace estimation ［J］.In Large-Scale Data Mining：Theory and Applications （KDD Workshop），2010.

［18］BURIOL L S，FRAHLING G，LEONARDI S，et al.Counting triangles in data streams ［C］／／The 25th ACM SIGMOD-SIGACTSIGART Symposium on Principles of Database Systems，June 26-28，2006，Chicago，Illinois，USA.New York：ACM Press，2006：253-262.

［19］PAVANY A，TANGWONGSAN K，TIRTHAPURAZ S，et al. Counting and sampling triangles from a graph stream ［J］. Proceedings of the Vldb Endowment，2013，6（14）：1870-1881.

［20］BULTEAU L，FROESE V，KUTZKOV K，et al.Triangle counting in dynamic graph streams ［EB／OL］. ［2015-07-14］.http：／／itu.dk／people／konk／papers／dtc_full.pdf.

［21］STEFANI L D，EPASTO A，RIONDATO M，et al.TRIEST：counting local and global triangles in fully-dynamic streams with fixed memory size［EB／OL］.［2016-02-24］.http：／／arxiv.org／abs／1602.07424.

［22］LIM Y，KANG U.MASCOT：memory-efficient and accurate sampling for counting local triangles in graph streams ［C］／／The 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining KDD，August 10-13，2015，Hilton，Sydney.New York：ACM Press，2015：685-694.

Research progress of triangle counting in big data

JIN Hongqiao，DONG Yihong
Faculty of Electrical Engineering and Computer Science，Ningbo University，Ningbo 315211，China

Counting triangles in a graph is an important step to calculate the clustering coefficient and the transitivity ratio of the network，which is widely used in important role identification，spam detection，community discovery，biological detection etc.Counting triangles algorithm is mainly faced with two major problems of space-time consumption and accuracy.The representative algorithm of the counting triangles in the big graph was introduced.There existed two kinds of algorithms，which were exact counting algorithm and approximate counting algorithm.Exact counting algorithms were divided into internal memory algorithm，external memory algorithm and distributed algorithm.The space-time consumption or I／O consumption of exact counting algorithm was very large. Approximate counting algorithms were divided into auxiliary algorithm，static algorithm and streaming algorithm.In the end，the counting triangles algorithms were summarized.

exact counting，approximate counting，triangle，graph

TP391

：A

10.11959／j.issn.1000-0801.2016169

金宏桥（1993-），女，宁波大学信息科学与工程学院硕士生，主要研究方向为大数据、数据挖掘。

董一鸿（1969-），男，博士，宁波大学教授，主要研究方向为大数据、数据挖掘和人工智能。

2016-04-05；

：2016-06-12