基于区间分析的机器人绝对定位精度分析方法

黄　康　何春生　甄圣超　洪　健　赵福民

合肥工业大学，合肥，230009

基于区间分析的机器人绝对定位精度分析方法

黄康何春生甄圣超洪健赵福民

合肥工业大学，合肥，230009

摘要：针对6R机器人绝对定位精度不高的现状，提出了一种基于误差的分析方法。该方法通过区间分析和POE方程对机器人误差进行建模，并通过修正一些区间运算规则得到更为准确的扩展区间运动学方程。分析了扩展区间运动学方程的层级特性，提出了一种易于扩展并且能有效降低区间依赖特性的层级区间运动学方程，并针对该方程由于过度扩展而无法得出精确结果的问题提出了一种区间矩阵优化方法。通过蒙特卡罗法以及和传统区间方法对比的仿真实验，验证了所提出方法更为高效，并且能够近似计算出理想的结果。某汽车变速箱装配线的6R机器人螺栓拧紧工序实验结果表明，所提出的分析方法比传统的区间方法更有效更精确。

关键词：POE方程；区间分析；绝对定位精度；6R机器人

0引言

由于机器人在制造、装配、控制等方面存在不可避免的误差，所以机器人的定位无法达到理想的目标。关于机器人定位精度的研究一直是学术界和工业界的热点[1-3]，早期的研究利用D-H参数[1]或者是修正的D-H参数[2]进行机器人运动学误差建模，另外一种研究思路则是利用POE(指数积)方程[4-6]或者是局部POE方程[7]建立误差模型。众多研究表明，相对于传统的D-H参数或者是修正的D-H参数进行误差建模，POE方程法具有明显的优点：①运动学模型相对于关节运动是光滑变化的，可以很好地保证不会出现奇异性问题；②只需建立全局坐标系和工具坐标系而无需建立众多局部坐标系。针对机器人误差的分析方法有模糊集法[8-9]、概率统计法[10]、区间方法[11]，前面两种方法均需要额外条件，如概率统计法需要大量的统计数据，而区间方法只需确定误差所隶属的区间即可，具有相当的优越性。

本文结合区间方法和POE方程对6R机器人的绝对定位精度进行研究。

1机器人基本参数及运动学模型

1.1理想运动学模型

某汽车变速箱螺栓拧紧工序6R机器人本体初始位形如图1a所示，图1b为该位形下机器人的结构简图，其中关节1和关节2轴线在x方向上重合。根据旋量理论[12]，机器人关节的运动可以表述为一个旋量运动，其中单位旋量为

(1)

式中，ω为旋量轴上的单位向量；q为旋量轴上的一个点向量；q×ω为旋量轴关于全局坐标系原点的矩。

(a)6R机器人本体初始位形

(b)6R机器人初始位形简图及坐标系建立图1　6R机器人

假定机器人在全局坐标系oxyz的初始位形为g(0)，每个关节的单位旋量为ξi(i=1,2,…,6)，那么机器人的运动学方程可以表示为

(2)

其中，θi是第i关节的运动偏置，并且有

(3)

其中，I是3×3单位矩阵，同时

(4)

式(4)被称为Rodriguez公式，∧是向量反对成化算子，对于任一向量ω=(ωx,ωy,ωz)，有

(5)

1.2实验平台及机器人基本参数

图2　6R机器人螺栓拧紧工序实验台

汽车变速箱机器人螺栓拧紧工序实验台如图2所示，该工序对机器人的绝对定位精度要求很高，式(2)中的机器人运动学各参数均为理想参数，而机器人实际设计中其结构参数ω、q均有一定公差，关节运动偏置θ由于传动和编码器精度也存在误差，因此它们均隶属于一定区间[13]，综合考虑设计公差以及测量仪器分辨率，得到初始位形下拧紧机器人的区间参数如表1所示。

表1　6R机器人区间参数

所有矢量均在全局坐标系oxyz中表示，该坐标系与机器人第一关节重合，如图1b所示。

2运动学误差模型及其层级特性

2.1修正区间运算规则

为了获得更为紧凑的扩展运动学误差模型，需要对区间数学规则作出修正，例如，机器人第一关节旋量轴方向向量区间中[ω1x]=[-10-5,10-5]，根据区间数学[14]，[ω1x]-[ω1x]=[-2×10-5,-2×10-5]，[ω1x]×[ω1x]=[-10-10,10-10]，而ω1x为实际机器人结构参数，仅为区间[ω1x]中一具体未知数值，[ω1x]-[ω1x]=0，[ω1x]×[ω1x]=[0,10-10]，可以看出按照区间数学的计算规则，模型计算出来的结果将会放大很多。

根据机器人的区间参数的实际意义，提出以下修正规则：

(6)

(7)

(8)

2.2扩展运动学误差模型

以修正区间规则为基础，推导机器人扩展运动学误差模型，在区间矩阵的乘法运算中，∀Am×n∈Rm×n,Bn×r∈Rn×r,[A]m×n⊂IRm×n,[Bn×r]⊂IRn×r，如果Am×n∈[A]m×n，Bn×r∈[B]n×r，那么Am×nBn×r∈[A]m×n[B]n×r。其中，IR为区间实数集。

设ω=(ωx,ωy,ωz)为机器人一关节旋量轴上的单位向量，[ω]=([ωx],[ωy],[ωz])是其对应的区间向量，那么可以得到：

(ω∧)2∈([ω]∧)2=[ω][ω]T-‖[ω]‖2I

(9)

(ω∧)3∈([ω]∧)3=-‖[ω]‖2[ω]∧

(10)

其中，I为3×3单位矩阵，给定θ∈[θ]，根据实数函数扩展到区间函数的根本定理[14]，有

(11)

结合式(9)、式(10)并利用式(7)，可将式(11)变为

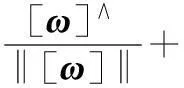
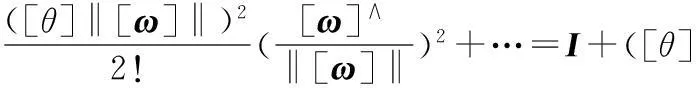
(12)

那么eω∧θ∈e[ω]∧[θ]，将区间根本定理扩展到矩阵中来，有

(13)

记θi∈[θi]，qi∈[qi]，ωi∈[ωi](i=1,2,…,6)，因而有

e[ξ1]∧[θ1]e[ξ2]∧[θ2]e[ξ3]∧[θ3]e[ξ4]∧[θ4]e[ξ5]∧[θ5]e[ξ6]∧[θ6]·

g(0)=[g(θ)]

(14)

式(14)称为机器人扩展运动学误差模型。

2.3误差模型层级特性

区间计算中，同一区间变量出现的次数越少，结果就越精确[14]，据此对式(14)进行变形，得到：

[g(θ)]=

e[ξ1]∧[θ1]e[ξ2]∧[θ2]e[ξ3]∧[θ3]e[ξ4]∧[θ4]e[ξ5]∧[θ5]e[ξ6]∧[θ6]·

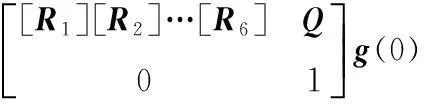
(15)

Q=[R1]([R2]([R3]([R4]([R5]((I-[R6])·

[q6]-[q5])+[q5]-[q4])+[q4]-[q3])+

[q3]-[q2])+[q2]-[q1])+[q1]

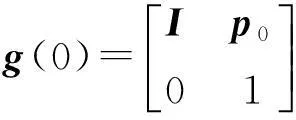
(16)

对于6R机器人，该计算方式计算次数为2×6(关节数)共12次。观察式(16)易知，该特性可以很容易扩展到其他n自由度的机器人，称式(16)表示的模型为机器人层级运动学误差模型。

3验证实验

为验证式(16)表示的层级运动学误差模型是有效的，利用6R机器人螺栓拧紧工序实验台进行实验，实验中机器人各关节运动量为θ1=0，θ2=π/6，θ3=π/4，θ4=θ5=θ6=0，利用水平三坐标测量机测量6R机器人执行器末端的位置。由于机器人各参数均在全局坐标系oxyz中表示，而三坐标测量机测量的数据均相对于它本身的坐标系，因此需要对数据进行坐标转换，测得螺栓拧紧执行器初始位姿为

将转换后的数据显示到MATLAB中，同时在德国汉堡大学开发的INTLAB区间分析工具环境下对式(16)进行蒙特卡罗法和区间计算仿真，将实验和仿真结果与文献[13]中推导的现有误差模型进行对比，结果如图3所示。

从图3a中可以看出，无任何优化条件下，蒙特卡罗随机点集和6R机器人实验台测量的点集均比现有误差模型和层级误差模型的区间边界小很多，尽管如此，层级误差模型的区间边界要比现有误差模型的区间边界更为紧凑，因此式(16)能够更精确计算执行器误差区间。图3b和图3c中蒙特卡罗点集和6R机器人实验台测量的点集分布区域在x、y、z方向基本一致并且层级误差模型的区间边界完全包含了实验台测量点集，因此基于修正区间运算规则的层级运动学误差模型能够用于分析该螺栓拧紧6R机器人的绝对定位精度。

4模型优化

4.1区间矩阵优化

为使得层级运动学误差模型能得到更精确的结果，对传统的区间优化方法进行改进，传统区间优化思路如下[14]。

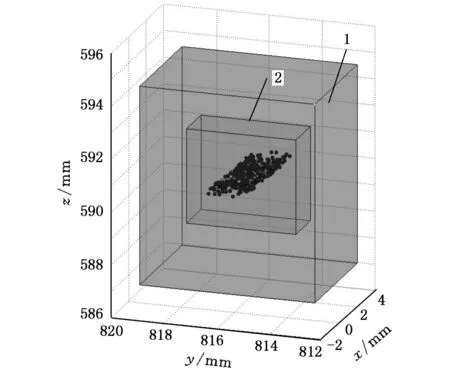
(a)无优化现有模型和层级模型对比仿真结果

(b)蒙特卡罗点集和实验台测量点集x、y方向的分布

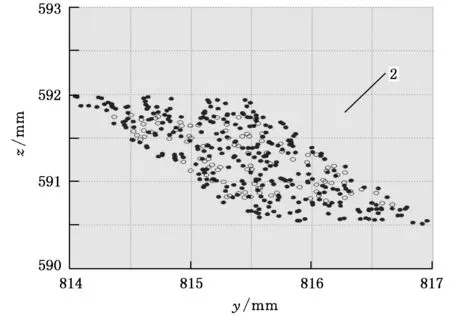
(c)蒙特卡罗点集和实验台测量点集y、z方向的分布1.现有模型区间边界　2.层级模型区间边界o实验测量点　·蒙特卡罗样本点图3　无优化现有模型与层级模型、蒙特卡罗点集和实验台测量点集结果对比

设区间向量

[A]=([a1],[a2],…[ai],…[an])⊂IRn

则

j=1,2,…,n

其中

并且

(17)

对实数函数f在定义区间上的区间扩展函数F，其区间优化可以表示成

(18)

传统区间优化方法对于多维到一维的区间扩展函数是十分有效的，然而，对于多维到多维的区间扩展函数，该方法效率非常低。

给定任一区间数[k]和区间向量[d]，假定[k]=[0,1]，[d]=([0,1],[1,2],[2,3])，则[b]=[k][d]=([0,1],[0,2],[0,3])，但是真实的区间分布要比[b]小很多，结果被扩大的关键在于[k]在计算过程中重复出现了3次，因此利用式(18)对[k]进行主要的区间优化计算，能有效减小区间的依赖效应，称在区间矩阵乘法中对区间系数进行区间优化的方法为区间矩阵优化。

4.2优化对比实验

4.2.1仿真结果

对图3中得到的结果进行优化并利用蒙特卡罗法进行对比仿真验证，其中对文献[13]中的模型利用传统区间优化方法进行优化，对式(16)利用区间矩阵优化方法进行优化，两者优化次数相同，观察式(16)以及式(12)可知，对模型计算扩大起主要作用的参数为θi∈[θi]，qi∈[qi](i=1,2,…,6)，因此对其进行区间优化，仿真结果如图4所示。

(a)现有模型传统区间优化和蒙特卡罗点集

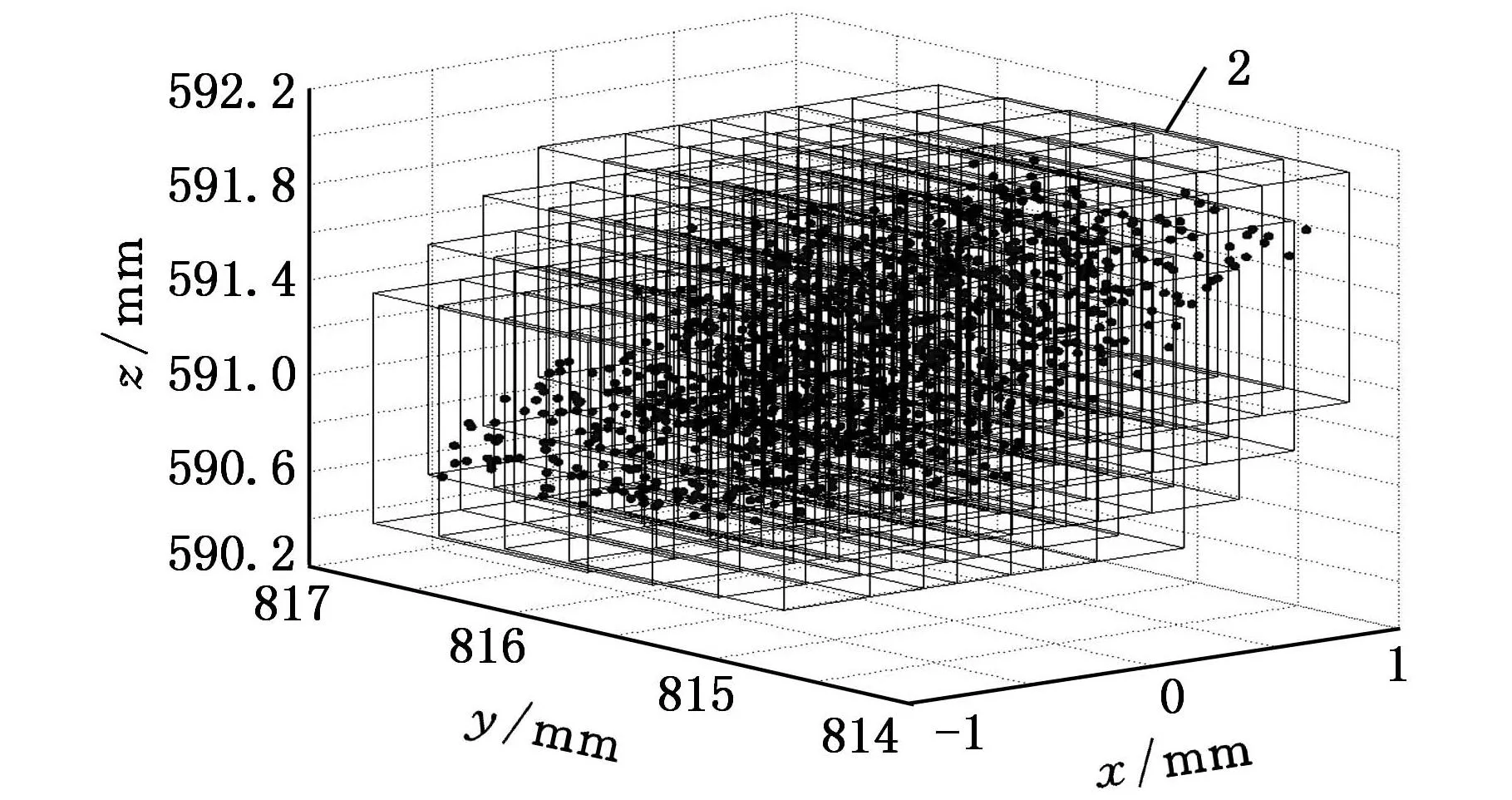
(b)层级模型区间矩阵优化和蒙特卡罗点集1.传统区间优化现有模型区间边界2.矩阵区间优化层级模型区间边界　·蒙特卡罗样本点图4　现有模型、层级模型优化和蒙特卡罗验证仿真结果

对比图3a和图4a可知，经过传统区间优化后，现有误差模型的区间扩大问题没有得到很好的改善，图4b表明引入区间矩阵优化后，层级误差模型的区间界基本上与蒙特卡罗点集相接，根据图3b和图3c中的结果，蒙特卡罗样本点与实验测量数据点集分布基本一致，仿真结果显示引入区间矩阵优化后的层级误差模型相对于传统区间优化后的现有误差模型，能够基本精确地计算机器人执行器的绝对定位分布区间。

4.2.2实验结果

对优化后的层级误差模型、现有误差模型与实验台测量数据进行分析，结果如图5、图6所示。

1.传统区间优化现有模型区间边界图5　现有模型传统区间优化和实验测量点集

(a)层级模型区间矩阵优化和实验测量点集

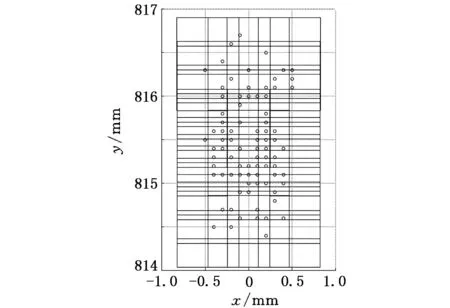
(b)层级模型区间矩阵优化和实验测量点集x、y方向分布

(c)层级模型矩阵区间优化和实验测量点集y、z方向分布2.矩阵区间优化层级模型区间边界　o实验测量点图6　层级模型矩阵矩阵优化边界和实验台实验结果

对比图5和图6a可知，层级误差模型经区间矩阵优化后的区间边界要比现有误差模型经传统区间优化后的区间边界更接近实验测量点集。结合图6b和图6c可知，优化后的层级误差模型区间在x、y、z方向与实验测量点集基本接近，但仍有些扩大，如果将优化次数增加就可以得到机器人执行器的准确定位分布，实验结果与图4中的仿真结果基本一致，因此本文提出的层级误差模型和区间矩阵优化方法是有效的。

将实验数据与仿真结果汇总得到表2，从表2可以看出，优化后的层级误差模型相对测量定位区域比ν和采用蒙特卡罗法得到结果基本一致，蒙特卡罗法定位间距与实验测量点定位间距差最大为0.56mm，而优化后的层级误差模型定位间距与实验测量点分布区域定位间距差最大为0.6mm，但是蒙特卡罗法需要计算1000次，而本文提出的方法只需计算128次，计算效率得到了很大提高。

表2　结果对比

5结论

(1)针对6R机器人区间参数的实际特性推导了基于修正区间规则的扩展运动学误差模型，并分析了其层级计算特性，在机器人螺栓拧紧实验平台以及MATLAB仿真中的结果均表明本文的模型比现有的区间模型更为精确。

(2)针对误差模型计算中由于区间依赖效应导致的结果过于扩大问题，提出了区间矩阵优化方法，通过对比实验，验证了区间矩阵优化方法比原有的区间优化方法更高效。

(3)优化后的层级误差模型与蒙特卡罗法计算的结果与实验得到的该螺栓拧紧6R机器人绝对定位区域分布基本一致，提出的模型及优化方法是合理的，并且其计算效率要比蒙特卡罗法高很多，因此该分析方法可以作为设计人员分析机器人操作精度的参考。

参考文献：

[1]VeitscheggerWK，HaurC.RobotAccuracyAnalysisBasedonKinematics[J].IEEEJournalofRoboticsandAutomation, 1986,2(3):171-179.

[2]ZhuangHanqi，RothZS，HamanoF.ACompleteandParametricallyContinuousKinematicModelforRobotManipulators[J].IEEETransactionsonRoboticsandAutomation, 1992,8(4):451-463.

[3]侯雨雷,段艳宾,窦玉超. 65m射电望远镜天线副面调整机构标定研究[J]. 中国机械工程, 2013, 24(24):3318-3322.

HouYulei,DuanYanbin,DouYuchao,etal．CalibrationofAdjustingMechanismforSubreflectorofa65MetersRadioTelescope[J].ChinaMechanicalEngineering，2013， 24(24): 3318-3322．

[4]ChenGenliang，WangHao，LinZhongqin.DeterminationoftheIdentifiableParametersinRobotCalibrationBasedonthePOEFormula[J].IEEETransactionsonRobotics, 2014,30(5):1066-1077.

[5]何瑞波，赵英俊，韩奉林，等. 基于指数积公式的串联机构运动学参数辨识实验[J]. 机器人, 2011, 33(1):35-39.

HeRuibo,ZhaoYingjun,HanFenglin,etal．ExperimentationonIdentifyingtheKinematicParametersofSerialMechanismBasedontheProduct-of-exponentialFormula[J].Robot，2011， 33(1):35-39.

[6]高文斌，王洪光，姜勇. 一种基于指数积的串联机器人标定方法[J]. 机器人, 2013, 35(2):156-161.

GaoWenbin,WangHongguang,JiangYong．ACalibrationMethodforSerialRobotsBasedonPOEFormula[J].Robot，2013， 35(2):156-161.

[7]YangaXiangdong，WuaLiao，LibJinquan，etal.AMinimalKinematicModelforSerialRobotCalibrationUsingPOEFormula[J].RoboticsandComputer-integratedManufacturing, 2014,30(3): 326-334.

[8]甄圣超，赵韩，黄康,等. 不确定机械系统的最优鲁棒控制设计：模糊法[J]. 控制理论与应用, 2014, 31(5):654-664.

ZhenShengchao，ZhaoHan，HuangKang,etal.OptimalRobustControlDesignofUncertainMechanicalSystems:AFuzzyApproach[J].ControlTheory&Applications, 2014,31(5): 654-664.

[9]甄圣超，赵韩，ChenYe-Hwa,等. 一种针对不确定机械系统的新型Lyapunov鲁棒控制方法[J]. 自动化学报, 2014, 40(5):875-882.

ZhenShengchao，ZhaoHan，ChenYe-Hwa,etal.ANewLyapunovBasedRobustControlforUncertainMechanicalSystems[J].ActaAutomaticaSinica, 2014,40(5): 875-882.

[10]RaoSS,BhattiPK.ProbabilisticApproachtoManipulatorKinematicsandDynamics[J].ReliabilityEngineering&SystemSafety, 2001,72(1): 47-58.

[11]WuWeidong，RaoSS.UncertaintyAnalysisandAllocationofJointTolerancesinRobotManipulatorsBasedonIntervalAnalysis[J].ReliabilityEngineering&SystemSafety, 2007,92(1): 54-64.

[12]MurrayRM，LiZexiang，SastrySS.AMathematicalIntroductiontoRoboticManipulation[M].BocaRaton:CRCPress, 1994.

[13]PacMR，PopaDO.IntervalAnalysisofKinematicErrorsinSerialManipulatorsUsingProductofExponentialsFormula[J].IEEETransactionsonAutomationScienceandEngineering, 2013,10(3):525-535.

[14]MooreRE，KearfottE，BakerR，etal.IntroductiontoIntervalAnalysis[M].Philadelphia,PA：SocietyforIndustrialandAppliedMathematics, 2009.

(编辑王艳丽)

An Absolute Positioning Accuracy Analysis Method for Robot Based on Interval Analysis

Huang KangHe ChunshengZhen ShengchaoHong JianZhao Fumin

Hefei University of Technology,Hefei,230009

Abstract：This paper proposed a method for improving the absolute positioning accuracy of 6R robot based on the analysis of error sources. A more precise and closer extended forward kinematics was deduced based on modified interval calculation rules and POE formula. Then a hierarchy interval kinematics was proposed,which was easy to extended to other kind of robots as well as handle interval dependency,and the overestimation of which might be eliminated by interval matrix refinement developed herein. Monte Carlo samples and the results of contrast simulation between the hierarchy interval kinematics and existing extended interval kinematics show the presented kinematics can get as tight results as desired results more efficient than the existing ones. The presented method was executed on a 6R robot of an automatic transmission assembly line that plays role of tightening screws. Experimental results show that the proposed approach is more efficient and accurate than existing analytic methods.

Key words：POE formula; interval analysis; absolute positioning accuracy; 6R robot

收稿日期：2015-07-27

基金项目：安徽省科技攻关计划资助项目(1301022085)

中图分类号：TP242.2

DOI：10.3969/j.issn.1004-132X.2016.11.009

作者简介：黄康，男，1968年生。合肥工业大学机械与汽车工程学院教授、博士研究生导师。主要研究方向为机构学、机械传动、汽车自动变速器、工业机器人技术。何春生，男，1991年生。合肥工业大学机械与汽车工程学院硕士研究生。甄圣超，男，1988年生。合肥工业大学机械与汽车工程学院讲师。洪健，男，1992年生。合肥工业大学机械与汽车工程学院硕士研究生。赵福民，男，1991年生。合肥工业大学机械与汽车工程学院硕士研究生。