《待定系数法求函数解析式》之方法小结

苏丽琼

(第五师中学，新疆 博乐　833400)

《待定系数法求函数解析式》之方法小结

苏丽琼

(第五师中学，新疆 博乐833400)

摘要：待定系数法求函数解析式是初中数学中是常用的方法，本文对待定系数法求函数解析式固定步骤进行了分析。

关键词：待定系数法求函数解析式；方法

函数是初中数学的重要内容，也是初中数学教学的难点。其中求函数解析式是初中数学主要内容之一，同时也是每年中考的重要考点之一，在初中阶段，学生主要学习正比例函数，一次函数，反比例函数和二次函数这几种类型。二次函数是联系高中数学的重要纽带,但作为每年中考的最后一道压轴题难倒了不少学生。我相信学生在做题时如果能根据不同的题目条件恰当地选择选用解析式类型，解题就会简单便捷，反之则繁琐无果。

无论针对哪一种函数，采用待定系数法求函数解析式都有其固定的步骤：

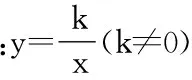
2.根据题目中恒等的条件，列出含待定系数的方程或者方程组。正比例函数和反比例函数都只需一个常量k即可确定函数解析式，所以只需一个条件，代入时，横纵坐标的值分别对应解析式中的自变量和函数值，得到一个一元一次方程：对于一次函数而言，它有两个常量k和b，所以通常需要两个条件组合成二元一次方程组；最难解的应当属于二次函数，它的表示方法多样，学生要根据条件进行合理的选择。

3.运用所学知识求出方程或方程组中未知数的值。

4.根据所求的值确定出函数的解析式。

待定系数法求函数解析式的步骤是固定的，但题目却是多变的。解题时只有读懂题意才能正确使用待定系数法而不是机械地模仿。一是文字描述题，代入所给的点即可：二是图像题，因为部分学生难以做到数形结合，因此看图求解析式就成了一个难点，要想解题首先要会识图：例如：图像是经过原点的一条直线对应正比例函数：图像是一条不经过原点的直线对应一次函数；双曲线对应反比例函数；抛物线对应二次函数，其次再选取经过图像上的点代入所对应的函数解析式，最后求出值确定出函数解析式。

分析：本题是利用图像求一次函数和反比例函数的解析式，点A在反比例函数的图像上，所以将点A代入解析式即可确定其解析式，点A、B在一次函数的图像上，但是B点的坐标不全，要先利用反比例函数的解析式求出点B的坐标，然后再用待定系数法求出一次函数的解析式。

又∵一次函数y=kx+b的图像经过点A(-2，1)与点B(1,-2)

∴一次函数的解析式是y=-x-1

例题2:如图，已知抛物线经过点A(﹣1，0)、B(3，0)、C(0，3)三点．求抛物线的解析式。

题目分析：本题已知了抛物线上的三个点的坐标，所以可利用待定系数法直接设二次函数的一般式求出该抛物线的解析式．

解：设抛物线的解析式为：y=ax2+bx+c(a≠0)

∵这个函数的图像过点A(﹣1，0)、B(3，0)、C(0，3)

∴抛物线的解析式：y=-x2+2x+3．

图像再分析：结合图象可知，题目所给三个点中A、B两点是图像与x轴的交点，所以可利用待定系数法设二次函数的交点式求出该抛物线的解析式。

解：设抛物线的解析式为：y=a(x-x1)(x-x2)(a≠0).

∵抛物线与x轴的交点是点A(﹣1，0)、B(3，0)

∴y=a(x+1)(x﹣3)

又∵抛物线经过点C(0，3)

∴a(0+1)(0﹣3)=3a=﹣1

∴抛物线的解析式：y=-(x+1)(x﹣3)=﹣x2+2x+3．

知识是一个日积月累逐步吸收的过程，要使每一位学生都能熟练掌握求函数解析式并不是一件容易解决的问题，作为教师，只有不断地去探索，去改变才能适应教学的需求。

(一)要不断丰富自己的内涵，增强自己的教学能力以适应教学中时刻变化的新情况。在教学中我深刻地体会到要想让学生真正理解和掌握求函数解析式的方法，教师应在给出相应典型例题的条件下，让学生自己去寻找答案，自己去发现规律。最后总结出每一种函数解析式的适用范围及一般应已知的条件，要让学生通过自主讨论，交流，合作的方式来探究学习中碰到的问题和难题，教师从中点拨，引导，并和学生一起学习，真正做到教学相长。

(二)要积极钻研教材，认真备课，对教材进行深加工，精心设置一题多解，一题多变、一法多用的数学问题。拓宽学生的知识面，培养学生举一反三的数学能力。

(三)要充分了解学生，给班级学生的能力准确定位，做到因材施教，分层次教学，提高教学和学习的双重效率。

中图分类号:G633.6

文献标识码：A

文章编号：1671-864X(2016)06-0129-01