预测新奥法施工的隧道引起的地面沉降



预测新奥法施工的隧道引起的地面沉降

1　城市隧道施工中估算地面沉降的必要性

在城市地铁隧道施工中估算地面沉降是工程中必不可少的重要组成部分，通常用以对既有建筑物进行风险评估，并提出建议：是否需要进行地层改良加固，是否需要对既有建筑物采取保护措施，以及如何选择适当的施工方法。

由于地铁沿线建筑物很多，在伊斯坦布尔软弱岩层中采用新奥法隧道施工，需要有一种快捷的、实用的估算地层变形的方法。

伊斯坦布尔亚洲一侧的地铁线路长约17 km，包括2个单洞的区间隧道（每隔250 m 设1个横通道），沿线有若干交叉渡线，以及16座地下车站。区间有些区段的隧道采用土压平衡盾构开挖，其中某些地质区段、横通道和交叉渡线段采用新奥法施工。16座车站采用明挖、暗挖相结合的方法施工。

隧道最初一段地质是黏土岩-砂岩，接着是石灰岩-砾岩，然后是泥岩-黏土岩-长石砂岩，最后一段是砂黏土-石灰岩，还有几处断层。大部分岩体质量评价值（RMR）为30～70，断层处岩体质量评价值较低。水文调查表明，渗透率很低（从10～6 m/s 到10～8 m/s），隧道工作面水流量小于5 L/s。沿线隧道覆盖层在20～40 m范围内变化。

各类隧道开挖断面见表1。

对区间、车站、交叉渡线隧道设计了11种不同的开挖断面，表1中展示的只是具有代表性的断面。隧道断面一般是由多圆心、多半径确定的，经换算可得隧道断面的换算半径。图1是典型的车站隧道断面（设站台）。

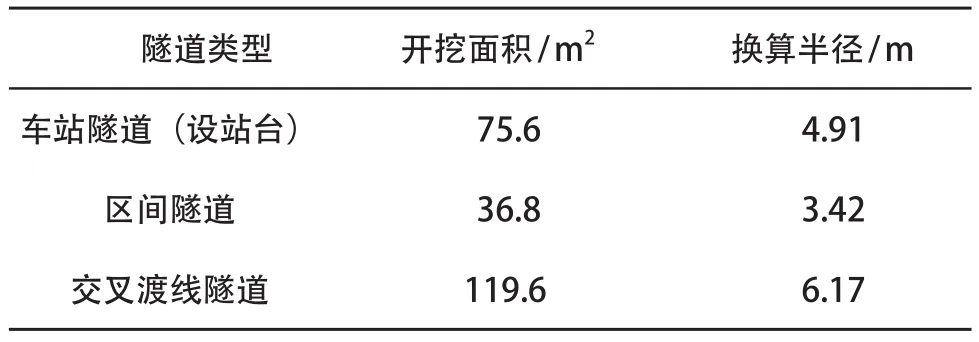
表1　各类隧道开挖面积

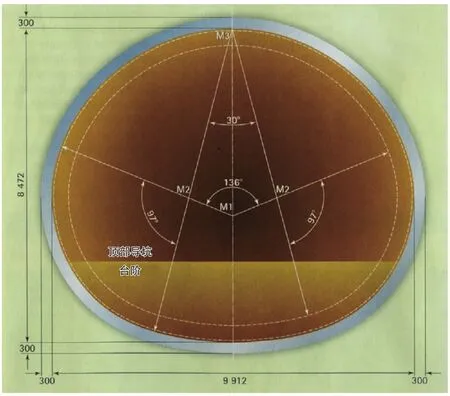
图1　典型的车站隧道断面（设站台）（单位：mm）

根据岩体质量评价值和不同的土工条件对每种断面设计了5个等级的初期支护，其区别在于喷混凝土厚度、格栅尺寸及其设置间距、拱顶锚杆长度及其数量，以及是否设置管棚。在完成初期支护、铺设防水层之后，现浇永久衬砌。防水层由土工布加 PVC 薄膜组成。永久衬砌厚度根据断面面积和岩石质量设计了3种类型。

隧道在建筑物密集的区域下面开挖，在开工之前，调查了隧道纵轴线两侧各50 m 的范围内3000幢建筑物。实际上隧道施工影响区是由技术规定确定的，那里的地面沉降预计会超过10 mm。根据第1次预测地面沉降值的结果，最大影响区宽80 m，小于最初调查的区域宽度100 m。

2　预测地面沉降的方法

在工程进展中，由于隧道尺寸的多样性、土工条件的不同，需要有一个系统分析的方法进行沉降值的预测。这个方法需要确定一些公式，选择输入参数来计算沉降曲线。

2.1Peck曲线

计算地层垂直沉降的表达式是半经验的正态分布曲线，它的输入参数是根据可获得的几何、土工信息资料，以及补充计算（例如收敛—约束法）确定的。

估算地面沉降的半经验法首先是由 Peck 于1969年提出的，他假定软土中的地层垂直沉降槽可以用高斯正态分布曲线来描述。之后，高斯模型得到进一步发展，提出了沉降槽宽度参数 K 和地层损失量 Vp的概念，给出了半经验公式，对隧道埋深、岩土特性、地层沉降特性做了适当处理。

根据高斯正态分布曲线计算垂直沉降的公式为：

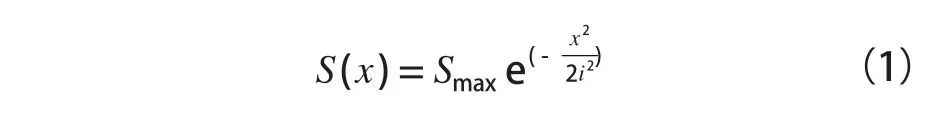
公式（1）中：S （ x ） 是离隧道轴线距离 x 处的沉降；i 是反弯点到隧道轴线的距离，它可以用公式 i = Z0K计算，Z0是隧道轴线的深度，K 是沉降槽的宽度参数；Smax是隧道轴线上的最大沉降，它可以表达为：

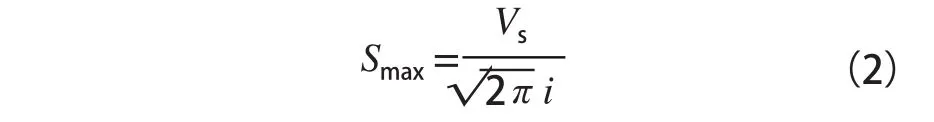
公式（2）中：Vs是隧道单位长度沉降槽的体积；Vtunnel是隧道理论开挖量，VL是超过隧道理论开挖量的体积，见图2。

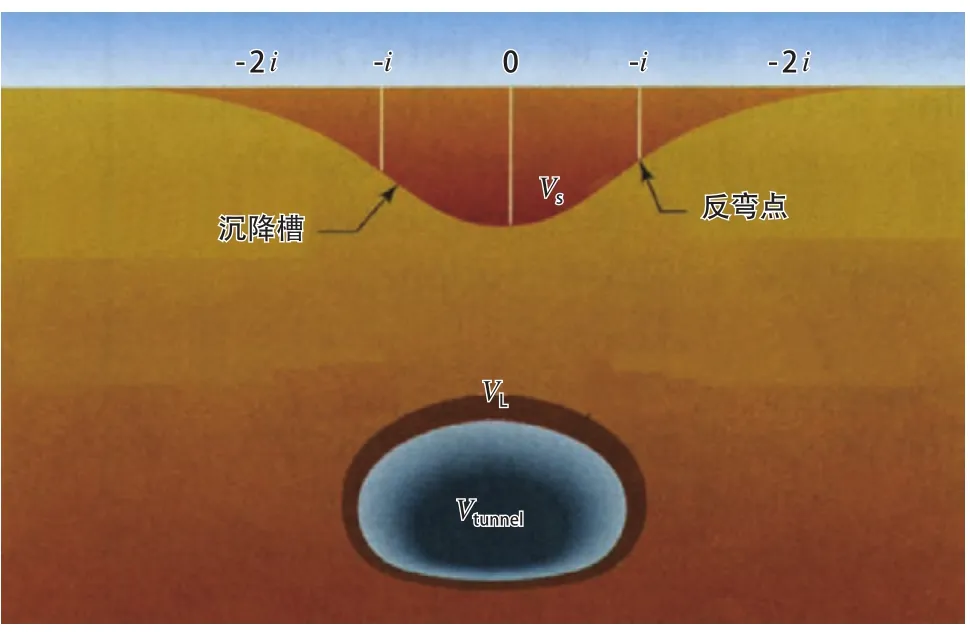
图2　沉降槽的高斯曲线和 VS、Vtunnel、VL的定义

2.2沉降槽宽度参数 K

经验的 K 参数描述沉降槽的宽度，它取决于地层的土工特性、隧道深度，在某些情况下还与开挖方法有关。K 可以根据隧道深度和土壤黏性来估算：

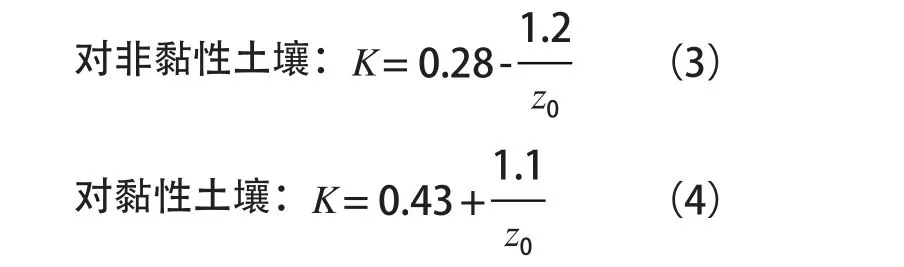
类似的研究表明：对颗粒土壤：K =0.2～0.3；对硬黏土：K =0.4～0.5；对非常软的砂黏土：K =0.7。

考虑了开挖地层的岩石特性和摩擦性状，K 参数根据隧道深度按黏性土壤公式（4）计算。考虑本工程最小和最大覆盖层分别为13 m和80 m，经估算 K 参数在0.495～0.443之间变化。

2.3地层损失量 Vp

地层沉降的原因是隧道开挖产生的地层损失量，它主要取决于地质构造及其应力状态、开挖速度、隧道断面大小和支护类型。它通常是用超过隧道理论开挖量的体积 VL除以隧道理论开挖量 Vtunnel的百分比表示的。

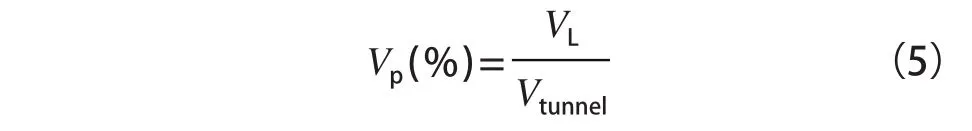
3　区间隧道上方地面的沉降曲线

采用收敛—约束法可以迅速计算沉降曲线和地层损失量。收敛—约束法，也称为应力—变形曲线法，它考虑了软弱岩体的变形和强度，以及支护能力和特性。

对7+640区段的区间隧道，可以根据 RMR 的最大、最小值确定相应的2套参数（表2），对有利和不利条件下2套参数进行地面变形曲线计算，采用的地层损失量 Vp为0.18% 和0.68%；K =0.471是采用公式（4）计算的，考虑了隧道深度27 m。图3展示了计算得到的有利和不利情况下的2条不同的地面变形曲线。可以推测，实际的地面变形就在这两者之间。

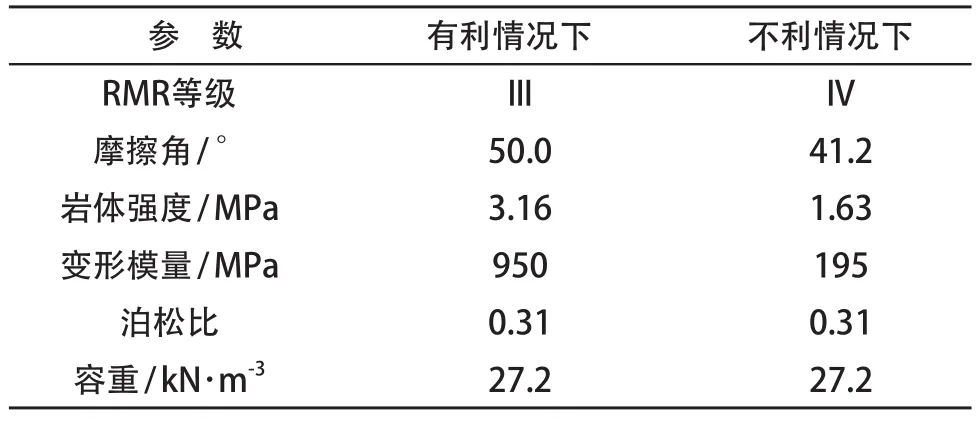
表2　7+640区段岩体参数

两隧道轴线距离小于3倍隧道直径时，应考虑2个隧道的相互干扰，第2个隧道的地层损失量应增加10%，这是由第1个隧道引起的早期地层松弛，由此产生不对称的沉降曲线。

4　车站隧道上方地面的沉降曲线

以7+640区段的 Umraniye 车站隧道为例，车站隧道由2个站台隧道组成，每个站台隧道的开挖面积为75.6 m2，等效半径为4.91 m，平均覆盖层为26.9 m，2个站台隧道的轴线距离为29.1 m。半经验法采用的Vp为0.51%（有利情况）和3.9%（不利情况），K =0.460。计算出有利和不利情况下2条不同的沉降曲线。利用监测的地面沉降数据拟合的高斯曲线反分析得出：Vp=2.0%，K =0.460。

计算地层变形曲线采用的岩体参数见表2。半经验法计算的有利和不利情况下2条车站隧道上方地面沉降曲线和拟合的高斯曲线见图4。

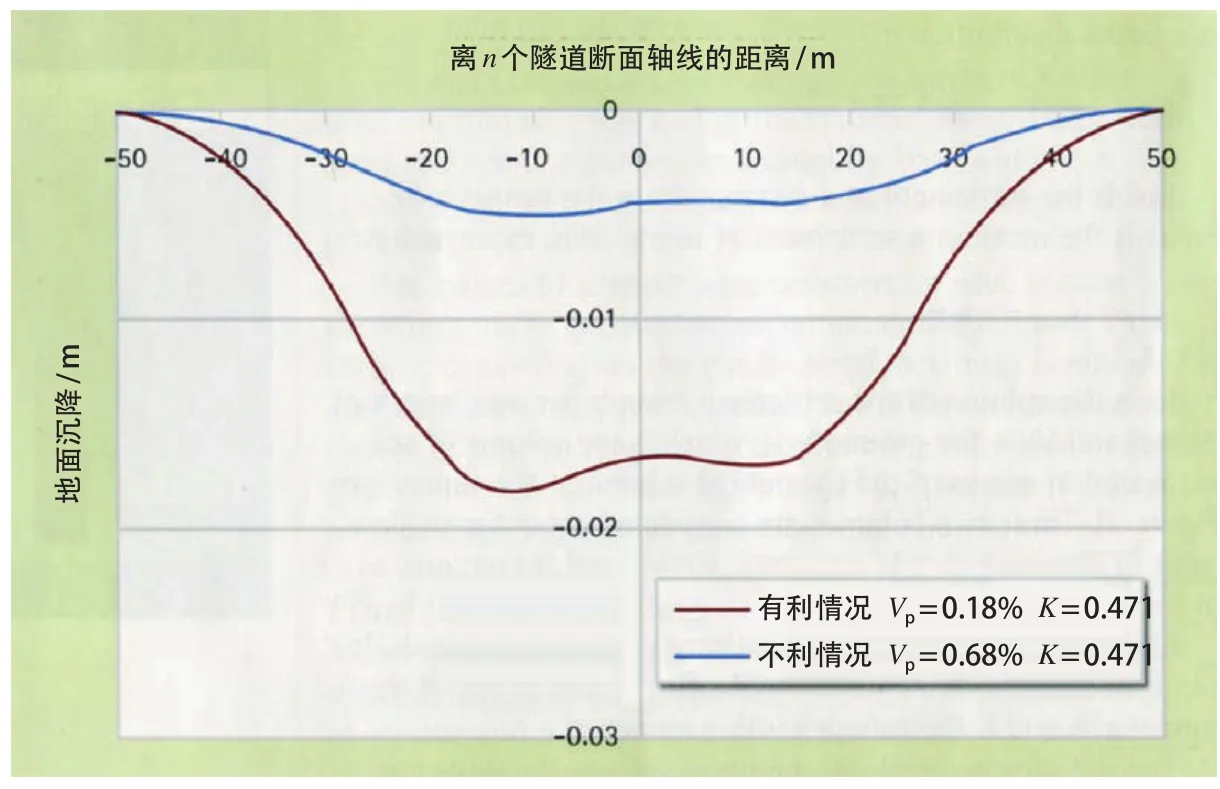
图3　区间隧道上方地面的沉降曲线

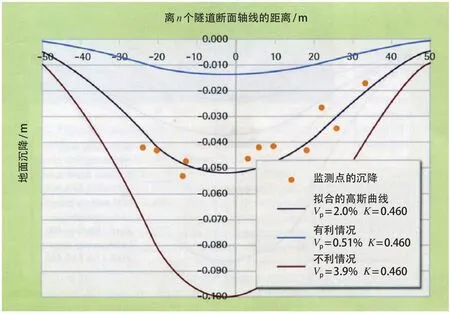
图4　车站隧道上方地面沉降曲线

5　交叉渡线隧道上方地面沉降曲线

交叉渡线段隧道的施工采用顶部导坑和台阶分部开挖，采取拱部和侧部设置锚杆的支护系统，有限单元模型可以模拟实际的土工情况、断面的几何形状、复制开挖步骤和支护系统。

有限元分析的地面垂直沉降可与半经验法预测的沉降、监测的地面沉降进行比较。在图5中，展示了有限元分析的垂直沉降曲线、用监测数据拟合的高斯曲线，以及半经验法在有利和不利情况下的计算曲线。

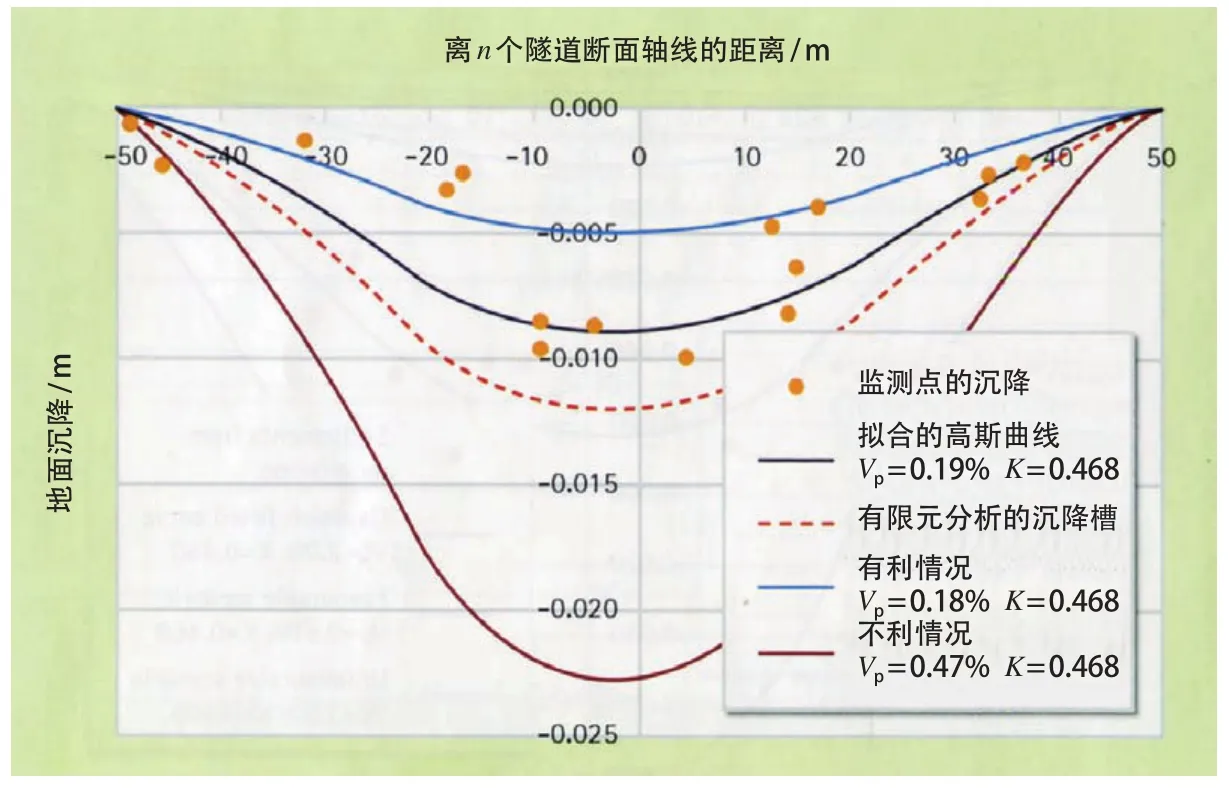
图5　交叉渡线隧道上方地面沉降曲线

用半经验法预测地面沉降采用的地层损失量 Vp为0.18%（有利情况下）和0.47%（不利情况下），K =0.468是采用黏性土壤公式（4）计算得到的。用监测地面沉降值拟合的高斯曲线反分析得出，Vp为0.19%，K =0.468。这表明对交叉渡线开挖面积，采用半经验法预测地面沉降也是适用的。

6　对反分析结果的分析

反分析是在半经验法预测沉降分析的基础上，利用从横向断面水准点获得的监测数据，使 Vp和 K 参数达到精细化，证实高斯曲线的适用性。

反分析的第1个结论是车站隧道上方地面运动的形状可以用高斯分布曲线来描述。值得注意的是 RMR 值越小（最差的岩体），这种情况就越明显，见图4。所记录到的地层运动能相当精确地用高斯曲线描述。

另一方面，根据反分析结果，由监测数据拟合的曲线校正的 K 宽度参数，与用黏性土壤公式（4）估算的 K 值是相等的。

反分析和有限元分析说明，在弱岩中用高斯曲线预测地面沉降有很好的近似性。

7　结束语

预测隧道施工引起的地面沉降，对于减小和预防既有建筑物的损害风险有重要的社会效益和经济价值。半经验的高斯正态分布曲线是最早的研究成果，采用有利、不利情况2套数据得出2条沉降曲线是一种有益尝试，可以界定实际的沉降曲线的上下限。利用监测地面沉降数据拟合高斯曲线的反分析更加贴近实际。有限元的分析模型，可以更加真实地进行数值模拟，它对半经验法计算的曲线起到验证的作用。比较这些方法，可以看出它们各有特色，又能相互印证、相互补充。

在这些研究成果与评估既有建筑物的损害风险之间，建立一种定量关系，使既有建筑物的风险评估更可信、更简捷，这是一个值得注意的研究方向。

参考文献

［1］ Sara Bech Padrosa，Nicola Della Valle. Predicting settlements from conventional tunnelling［J］. Tunnels & Tunnelling International，2015（2）：37-43.

邵根大 编译

责任编辑 冒一平

收稿日期2015-12-14