流化床蒸发器中石墨管振动位移特性

安敏，刘明言,，徐晓萍(天津大学化工学院，天津化学化工协同创新中心（天津），天津 30007；化学工程联合国家重点实验室(天津大学)，天津 30007)

流化床蒸发器中石墨管振动位移特性

安敏1，刘明言1,2，徐晓萍1
(1天津大学化工学院，天津化学化工协同创新中心（天津），天津 300072；2化学工程联合国家重点实验室(天津大学)，天津 300072)

摘要：借助振动传感器和静动态信号测试分析系统，采用标准偏差、功率谱和小波分解等方法，对汽液固三相外部自然循环流动沸腾流化床蒸发器中石墨管的振动位移行为进行了研究。结果表明：具有多尺度特性的原始完整的振动位移信号可以分解为低中频信号和高频振动信号；原始信号和低中频振动位移信号的标准偏差随加热蒸汽压力的增加先增加而后趋于稳定，高频振动信号则缓慢增加；在汽液两相系统中，颗粒的加入和流化抑制了石墨管的低中频振动行为，增强了高频振动行为；高频信号的标准偏差随固含率增加而显著增加；振动行为随粒径增大有所增强；研究了石墨管不同轴向位置处的振动规律；根据实验数据拟合得到了两相及三相条件下，石墨管振动强度的关联式。

关键词：汽液固三相流；石墨管；蒸发；振动位移；多尺度；安全

2015-10-12收到初稿，2015-12-03收到修改稿。

联系人：刘明言。第一作者：安敏（1990—），硕士研究生。

Received date: 2015-10-12.

引　言

汽液固三相循环流化床蒸发器因其具有在线防垢和强化传热的特点而在化工、轻工、医药、能源和环境等领域具有广泛应用[1-4]。在将其扩展改造应用于稀磷酸等强腐蚀性介质的蒸发浓缩时，由于这类蒸发器的换热管一般采用抗腐蚀能力强、换热效果好的石墨材质制造[5-6]，而石墨属于脆性材质，对于有着高压、强烈振动冲击和频繁水锤现象的运行环境，需要谨慎对待[7]。因此，有必要考察固体颗粒的加入和流化对蒸发器内石墨加热管的机械振动行为的影响，评估将三相流化床蒸发浓缩技术引入石墨类蒸发器的安全可行性。这方面的研究国内外尚属空白。

国内外开展了多相流体激发的管道振动行为的流固耦合研究[8-10]，振动机理也逐渐发展，涉及泊松耦合、结合部耦合、摩擦耦合和Bourdon耦合等[11-12]。但是，研究主要侧重于管道振动行为的建模及通过有限元等方法求解管道的固有频率和固有振型，针对汽液固三相流对管道振动的影响的实验研究尚未见报道。

关于振动行为的信号分析，主要考察其时域、频域、时频域以及非线性特性。时域分析[13-15](包括标准偏差、峰度、峭度等)和频域分析[16-18](包括频谱和功率谱等)已被广泛应用于压力、振动、电导率等信号的分析，考察流化床的气泡特性和不同流型转变，评估流态化效果等。针对多相流体系中广泛存在的多尺度行为，小波分解作为一种时频域分析方法是研究信号多尺度特性的有力工具[19-21]。如Li 等[20]将气固流化床中由光纤探针采集到的信号分解为微尺度、介尺度和宏尺度3个子信号，并分别研究了不同尺度的行为。

本文建立了单根石墨管汽液固三相流外部自然循环流化床蒸发器以及振动位移测试及动态信号自动采集系统。石墨管的振动行为由加速度振动传感器感知，再进行A/D转化和硬件积分后，由静动态测试系统得到原始振动位移信号。针对蕴含振动信息的振动位移时间序列数据，采用时域、频域和小波分解等对其进行分析，考察振动信号不同方面的特性，进而对石墨管在三相流影响下的振动行为进行研究。首先运用功率谱密度函数确认了振动位移信号的多尺度特性；再利用小波分解将原始完整的振动位移信号分解为低中频振动位移信号和高频振动位移信号，低中频振动信号是原始振动信号中的线性成分，高频振动信号通过滤掉原始信号中的线性成分后得到；最后考察这3种振动信号的标准偏差随加热蒸汽压力、固含率、粒径和石墨管轴向位置的变化规律。

1　实验设备和分析方法

1.1实验装置及流程

建立的单根石墨管汽液固三相外部自然循环流化床蒸发器及振动信号测试采集系统如图1所示。实验装置的主要测试部分是1个单管套管式换热器。其中，内管为石墨管，长度为1.1 m，外径为37 mm，壁厚为6 mm。实验所用的液相是蒸馏水，固相为玻璃球，密度为2500 kg·m−3，平均直径分别为1.3、2.4、3.5 mm。来自锅炉的饱和蒸汽在换热器的套管环隙内冷凝放出潜热，管内液体吸收该潜热温度升高，当管内流体的温度上升至沸点时开始沸腾。由于气泡在加热管内部不断生成，致使加热管和循环管内流体的密度差不断加大，进而在加热管和循环管间形成汽液两相自然循环流动。加入颗粒之后，颗粒在流体的作用下行成循环流态化，最终形成稳定的汽液固三相自然循环流动。石墨管内的三相流体向上流动，进入汽相和液固相的分离器进行分离，分离的蒸汽进入二次蒸汽冷凝器，经冷却水冷凝后，重新泵回系统，而液固两相流体则由循环管进入加热管重新开始循环。图2是汽液固三相流动沸腾条件下，循环管可视化视窗内典型的颗粒运动图片。

根据不同颗粒含量对蒸发换热过程的增强效果以及常用加热蒸汽压力的范围[21]，选定实验过程中加热蒸汽压力为70、90、110、130、150 kPa，固含率为0、0.5%、1.0%、1.5%、2.0%。

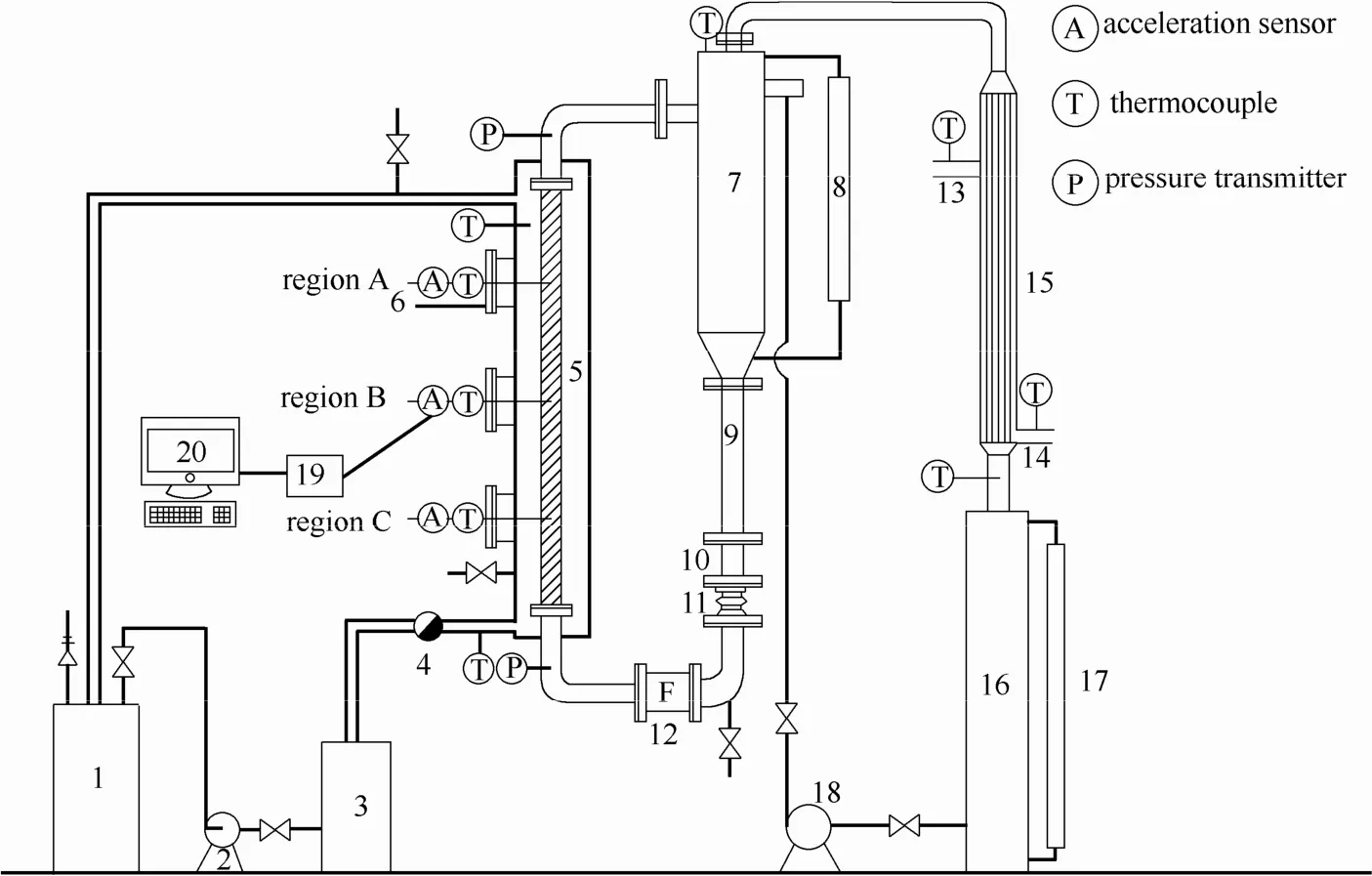
图1　汽液固三相外部自然循环流化床蒸发器及振动信号测试采集系统Fig. 1 Apparatus and flow diagram of fluidized bed evaporator with vapor-liquid-solid external natural circulating flow and measuring system of vibration signal1—boiler; 2—centrifugal pump; 3—steam condensate tank; 4—steam trap; 5—graphite tube; 6—shell side of heater; 7—separator; 8—level gauge; 9—circulating tube; 10—visual window; 11—spring; 12—electromagnetic flowmeter; 13—outlet of cooling water; 14—inlet of cooling water; 15—vapor condenser; 16—vapor condensate gauge tank; 17—level gauge; 18—magnetic drive pump; 19—data acquisition system; 20—PC

图2　汽液固三相流动沸腾体系可视化部位的典型图片Fig. 2　Typical image of vapor-liquid-solid flow boiling system in visual window with P =110 kPa, ε =2.0% and ds=2.4 mm

1.2振动传感器及数据测试采集系统

由于满足精度要求的位移计体积较大不能进入套管环隙，因此石墨管的振动位移行为由加速度传感器(扬州英迈克公司的2107型，灵敏度52.6 pc·g−1)检测，得到的电荷信号经电荷适配器进行阻抗变换、交直流变换和硬件积分后，由静动态信号测试分析系统(江苏泰斯特电子设备公司的TST5915)进行记录，得到振动位移信号。由于本文的振动行为的频率成分复杂，无法直接利用加速度二次积分的方法得到位移信号，即使是利用信号测试分析软件中的软件积分，误差也高达30%，所以只能实验采集以硬件积分形式实现的振动位移信号。两次硬件积分的最大误差为8%。振动加速度传感器适于测量高频振动行为，多用于流化床流体力学性质的检测，而振动位移信号能更为准确地考察中低频振动行为[22]，振动位移的大小可直观地展现振动行为的强弱，常用于评估管和轴的振动安全性。3个加速度传感器通过铝制卡箍紧固于石墨管上，并沿轴向四等分石墨管。3个传感器分别固定在测量点A(H/L=0.75), B(H/L=0.50)和C(H/L=0.25)。振动位移信号采样频率为5 kHz，在系统稳定状态下采集6 min样本长度的实验数据。

石墨管的外壁温和内部流体温度分别由金属表面热电偶(RDF20109型)和铠装热电偶(沈阳中色)测量。所有热电偶标定的线性相关度都在0.999之上，可准确捕捉温度的瞬态变化。加热管的进出口压力由压力变送器测得。电磁流量计用来测量多相流的循环流量。温度、压力和循环流量信号采用JM3840测试分析系统(扬州晶明)进行信号的记录分析，采样频率均为200 Hz，在系统稳定状态下采集6 min样本长度的实验数据。实验过程中采集温度、压力和循环流量信号，除了用于三相流蒸发器的压降和传热特性计算外，还有两个目的。一是通过压力、温度和流量等基本参量的测量，分析评估多相循环流动状况，进而确定振动信号的测取时机；二是为了获得建立振动强度关联式的基础数据。

1.3振动位移信号分析方法

1.3.1标准偏差和功率谱密度函数标准偏差(standard deviation)用来衡量时间序列数据偏离平均值的程度。鉴于振动行为的对称性，本文振动位移时间序列的平均值接近于零，所以，振动信号的标准偏差等价于振动信号的有效值。同时振动位移行为的振动强度与振动位移有效值呈正比[22]，因此，振动信号的标准偏差可用于表征振动强度的大小。其计算公式如式(1)和式(2)所示。

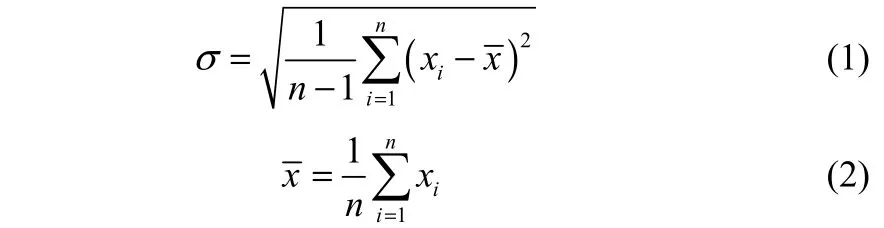
功率谱密度函数(power spectral density function，PSDF)用来分析振动信号的频域特点，是分析振动原因和机理的重要数据。功率谱分析采取数据分段进行加窗处理后，由傅里叶变换得到每段谱估计，并求总平均。功率谱基本计算式如下

式中，w(n)为窗函数，x(i)代表信号，f为分解的不同正弦波的频率，Pxx(f)对应频率正弦波的幅值，j为虚数单位。

主要采用Matlab中的pwelch函数实现振动位移信号的功率谱分析，基本公式见式(3)[23]。

其中，窗函数(window)采用汉明窗，重叠率(overlap)设定为50%，FFT算法的长度(nfft)设定为32768，fs为信号的采集频率，Pxx是某一特定频率f时的平均功率谱估计值。

1.3.2小波分解分析小波分解(wavelet transformation analysis)具有将原始信号分解成不同频段的成分，并重建成为独立的子信号的功能，即实现信号的多尺度分解[19-20]。本文采用db2小波函数将原始振动信号分解8次，原始信号被分为9个子波(a8, D1～D8)。相对来说，a8代表原始振动信号的低频成分，是信号的主轮廓，D1～D8代表原始振动信号的高频成分，是信号的细节部分[19]。

2　结果与讨论

2.1多尺度特性判定——振动位移信号的时间序列和功率谱分析

图3(a)是单相常温液体静止、单相液体缓慢流动、汽液两相沸腾流动、汽液固三相沸腾流动4种不同流动状态下，石墨管中部(测量点B)的振动位移信号的时间序列图。在实验开始后15 min时(锅炉预热，采集系统正常工作，管内液体未升温)采集单相常温静止液体条件下的振动位移信号[图3(a)曲线a]，作为单相、两相和三相流动条件下的空白对照。管内液体升温过程中形成的缓慢的单相液体流动[图3(a)曲线b]可激发微弱、均匀和周期性的管子振动位移行为。图3(a)曲线c是汽液两相沸腾流动条件下激发的振动位移信号，信号幅值出现显著波动。原因可能是大气泡的生成、流动和破裂等行为造成石墨管内压力不平衡，进而激发大幅度的位移振动行为。加入固体颗粒之后，图3(a)曲线d呈现出相对规则的周期性位移振动行为，对应管内形成的稳定的汽液固三相外部自然循环沸腾流动，同时，规整波动时间序列上附加出现了尖刺状的高频小幅波动现象。这是因为颗粒的加入抑制了大气泡的生成和气泡的湍动程度，进而减轻了压力不平衡现象；颗粒间、颗粒与管壁间的局部激烈碰撞，激发出高频的振动位移行为。

图3(b)中展示了上述4种流动条件下[图3(a)]的振动位移信号的功率谱图。静止液体条件下的振动位移信号[图3(b)曲线a]的功率谱为约3 Hz的峰，该峰在单相、两相和三相流动条件下的功率谱图中也都有出现，无明显变化，归类为测试系统的干扰信号。

单相、两相和三相流动条件下[图3(b)曲线b、c和d]，振动位移信号的功率谱图都存在与时间序列的周期行为相对应的尖峰，主频都在8 Hz左右。系统加入颗粒之后，功率谱图在50～80 Hz处出现微弱峰群，对应于图3(a)曲线d的高频尖刺状波动。

因此，振动位移信号的功率谱图主要由对应于流体流动和大气泡行为的低中频成分(8 Hz左右)和对应于颗粒行为的高频成分(50～80 Hz)两部分组成。

2.2多尺度成分分解——振动位移信号的小波分解

图3　不同流动状态下石墨管中部振动位移信号的时间序列和功率谱Fig. 3　Time series and power spectra of vibration displacement signals of graphite tube in measuring point B at varied situationsa—static liquid phase with room temperature; b—P=70 kPa, single-phase liquid flow; c—P=70 kPa, vapor-liquid boiling flow; d—P=70 kPa, ε=2.0%, ds=2.4 mm, vapor-liquid-solid boiling flow

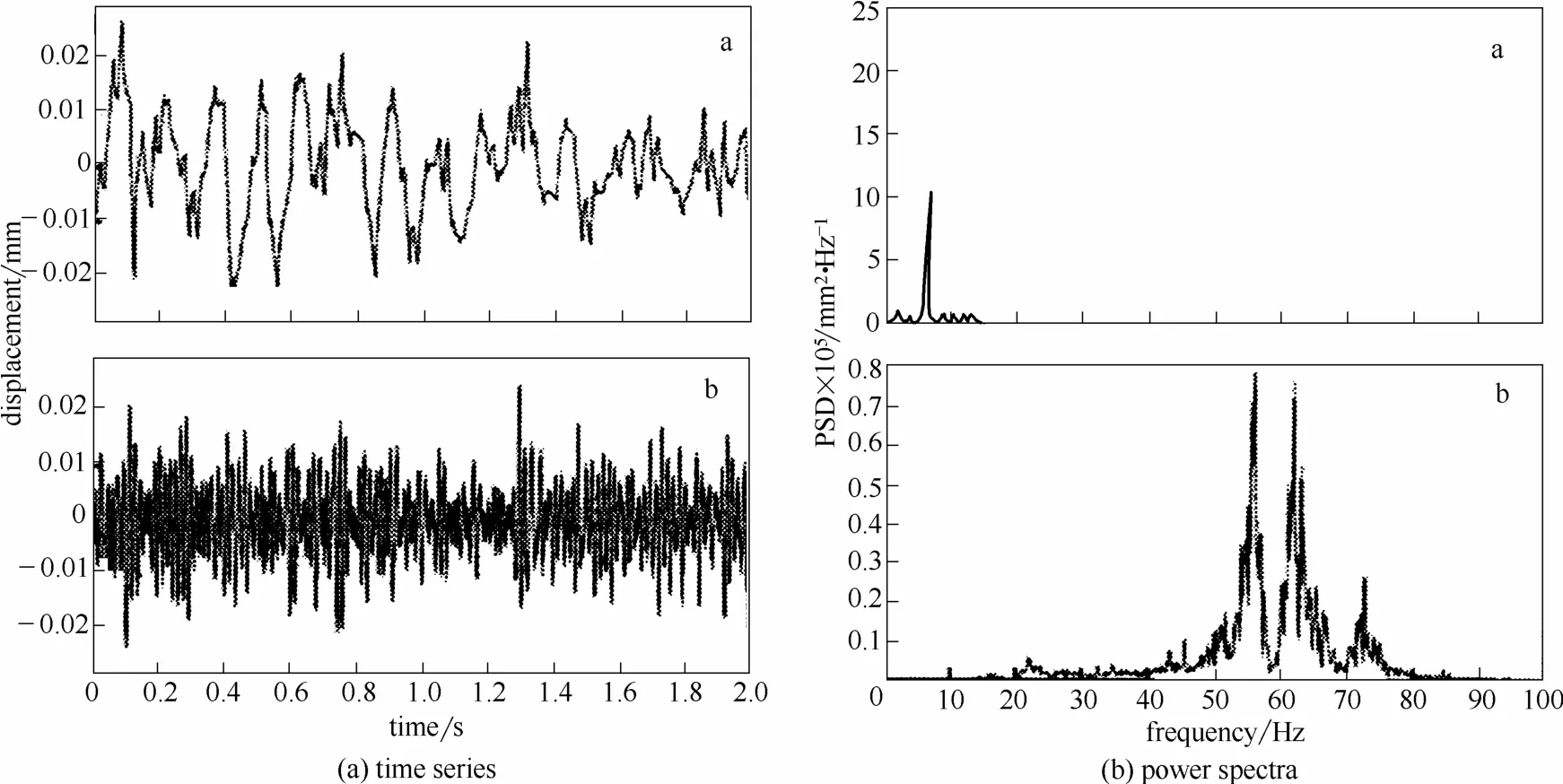
图4　原始振动位移信号小波分解重建的低中频成分和高频成分的时间序列和功率谱图Fig. 4　Time series and power spectra of low-middle-frequency and high-frequency components of original vibration displacement signal after wavelet transformation and reconstruction(P=70 kPa, ε=2.0%, ds=2.4 mm) a—LFS/MFS; b—HFS

振动位移信号的功率谱图(图3)表明，振动位移信号包含两个尺度的成分。其中低频的流体流动和中频的气泡行为激发的振动信号的频率成分相近，集中于0～20 Hz (图3曲线b、c)；众多颗粒碰撞激发振动信号的高频成分，主要分布在20～100 Hz(图3曲线d)。结合小波分解的原则[19]和振动信号功率谱图特点，进行了两个成分的分离：一是原始振动位移信号的线性成分，由a8、D8和D7子波叠加重建形成，其频率范围为0～20 Hz，对应流体和气泡行为的低中频宏观尺度运动(low-middlefrequency vibration signal, LFS/MFS)；另一个是原始振动信号的连续增量成分(滤掉原始信号中的线性成分得到)，由D6～D1子波叠加重建形成，频率范围为20～100 Hz，对应颗粒行为的高频微观尺度运动(high-frequency vibration signal, HFS)。图4是汽液固三相流条件下，振动位移信号小波分解重建后的低中频成分和高频成分的时间序列和相应的功率谱图。

2.3多尺度成分特性——振动信号的标准偏差分析

原始的振动位移信号分解为表征流体和气泡行为的宏观低中频信号(LFS/MFS)和表征微尺度的颗粒行为的微观高频信号(HFS)。在此基础上重点考察原始振动信号、小波分解获得的低中频振动信号和高频振动信号的标准偏差随加热蒸汽压力、固含率、颗粒粒径和石墨管轴向位置的变化规律。相对于仅考察原始振动信号，经小波分解的不同尺度成分的分析能更深入地探究振动的规律和机理，从而在原因明确的条件下更好地认识石墨管振动行为和评价振动安全性。

2.3.1加热蒸汽压力的影响图5中每条曲线对应的是不同固含率条件下，各频段信号的标准偏差随加热蒸汽压力的变化规律。

在三相沸腾流动条件下，低中频振动信号的标准偏差随蒸汽压力先增加后略有减小。低中频信号对应流体和气泡的行为。可视化研究表明，汽液固三相流化床蒸发器的加热管内，上部为汽液固三相流区，下部为液固两相流区[24]。当形成稳定的多相外部自然循环沸腾流动时，三相区内气泡的生成和被流体带离达到平衡，管子上部形成一定长度的稳定的三相区。在不同蒸汽压力条件下，三相区内的大气泡数量和湍动程度，均随蒸汽压力的增加而增加，气泡对石墨管的作用频率和强度均增加。因此，大气泡对振动行为的影响增强。管内流体的循环流动的推动力来自于加热管和循环管内流体的平均密度差。该密度差随三相区长度的增加而加大，流体的循环流速也增加，流体流动对振动行为影响增强。当加热蒸汽的压力增加到一定程度后再增加时，循环速度将更快，从而将大气泡快速带离加热管，减弱了气泡的影响，低中频振动强度略有下降。汽液两相沸腾流动条件下，低中频振动信号的标准偏差随蒸汽压力的增加先增加后稳定（图5），增加幅度大于三相沸腾流动条件下的值。相同蒸汽压力条件下，两相流中没有颗粒的作用，大气泡的振动行为更加激烈，激发的振动随加热蒸汽压力的增加而显著增强。

图5　石墨管中部低中频和高频振动信号的标准偏差随蒸汽压力的变化规律Fig. 5　Standard deviations of separated LFS/MFS and HFS of vibration displacement signals versus heating steam pressure at varied solid holdup in measuring point B with ds=2.4 mm ■ V-L flow, LFS/MFS; □ V-L flow, HFS; ● 0.5%, LFS/MFS; ○ 0.5%, HFS; ▲ 1.0%, LFS/MFS; △ 1.0%, HFS; ◆ 1.5%, LFS/MFS; ◇1.5%, HFS; ☆ 2.0%, LFS/MFS; ★ 2.0%, HFS

如图5所示，高频信号的标准偏差随蒸汽压力略有增加。高频信号对应于石墨管内颗粒的碰撞行为。石墨管内参与循环的颗粒数目随蒸汽压力增加而略有增加[24]，因此，颗粒与管壁碰撞的频率增加。同时，增加蒸汽压力，流体的湍动程度增加，颗粒与管壁碰撞的力量有所增加，所以高频行为呈现增强的趋势。值得注意的是，低中频信号的标准偏差总是大于高频信号的，但随着固含率的增加，该差值逐渐缩小。颗粒对振动行为的影响程度随固含率增加而逐渐增强，在汽液两相(0)及低固含率(0.5%、1.0%、1.5%)条件下，振动位移行为受流体和气泡影响较大，在高固含率时(2.0%)，颗粒与气泡对振动行为的影响程度近似相同。

图6是不同的固含率条件下，原始振动信号的标准偏差随蒸汽压力的变化规律。在实验范围内增加蒸汽压力，三相沸腾流动条件下振动位移信号的标准偏差先增加后略有下降，即达到波动性稳定状态，而两相沸腾流动条件下的振动位移信号的标准偏差则是先增加后稳定。尤其是较高的蒸汽压力条件下，三相的原始振动位移信号的标准偏差小于两相的，意味着较高蒸汽压力条件下，一定量颗粒的加入可以降低汽液两相沸腾流动激发的石墨管的振动位移行为。如图5所示，两相沸腾流动条件下，低中频振动位移信号的标准偏差大于本实验考察的所有三相沸腾流动条件下的；同时两相高频振动位移信号的标准偏差均低于所有三相条件的。说明固体颗粒的加入，明显地抑制了低中频的振动位移行为，增强了高频的振动位移行为。颗粒对低中频振动行为的抑制作用源于颗粒对已有大气泡的破碎作用以及振动系统质量的增加。图3的振动时间序列可体现颗粒对气泡的抑制作用，进而抑制低中频振动强度。颗粒加入之后，颗粒与管壁频繁撞击，激发高频振动位移行为，因此三相沸腾流动系统的高频振动位移信号的标准偏差大于两相沸腾流动系统的。

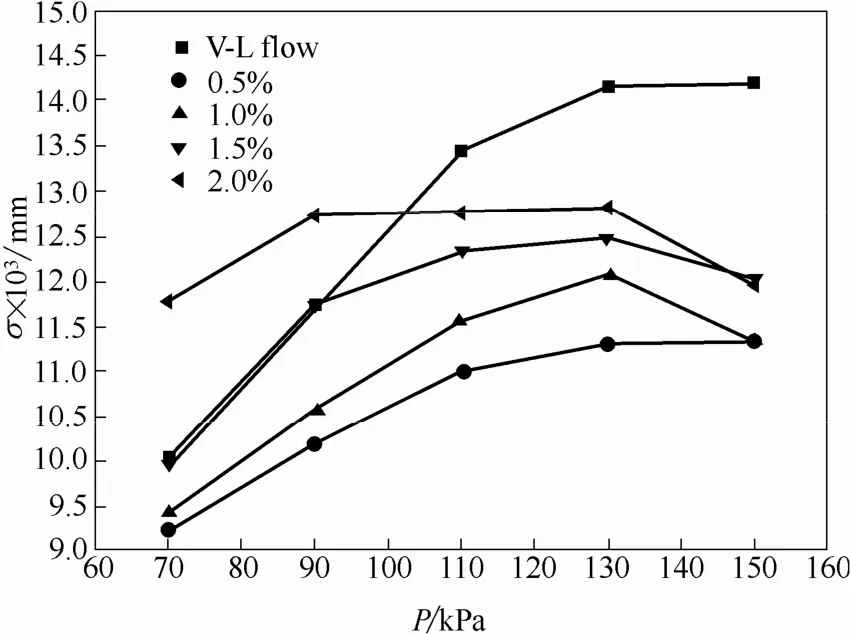
图6　石墨管中部原始振动信号的标准偏差随蒸汽压力的变化规律Fig. 6　Standard deviations of original vibration displacement signals versus heating steam pressure at varied volume fractions of solid particles in measuring point B with ds=2.4 mm

2.3.2固含率的影响从图6还可以观察到：汽液固三相流动激发的振动位移信号的标准偏差随固含率的增加而逐渐增大。增加固含率，低中频信号基本稳定，只是在较高固含率时(2%)略有下降。可视化研究表明[24]，固含率对三相区长度的影响较小，进而流体和气泡行为也变化不大，所以固含率对低中频振动行为影响很小。不同于低中频信号，高频信号的标准偏差随固含率明显增加。其原因为：随着固含率的增加，加热管内颗粒的浓度增大，颗粒与管壁的碰撞频率增加，因颗粒碰撞产生的高频振动行为也增强。

在汽液两相沸腾流动条件下，加入固体颗粒，形成了三相沸腾流动，此时低中频振动位移信号的标准偏差出现减小趋势，可归因于颗粒对石墨管内大气泡的破碎作用。由于实验范围内，颗粒的加入对高频振动行为的增强程度有限，所以三相沸腾流动系统的原始振动信号的标准偏差基本低于两相沸腾流动下的值。同时，与加热蒸汽的压力也有很大关系。只有在较高固含率（2%）和较低加热蒸汽压力的条件下，才会出现三相沸腾流动系统的原始振动信号的标准偏差大于两相沸腾流动下的值，如图6所示。

在两相条件中加入固体颗粒和增加三相条件中颗粒含量，固体颗粒对振动行为的影响程度不同。当固含率较大时，管内稳定的小气泡较多，小气泡对颗粒作用不大，所以，低中频振动行为基本不变。而颗粒对高频振动行为的影响总是随固含率的增加而增强，所以，三相原始振动位移信号的标准偏差随固含率的增加是增加的。

2.3.3粒径的影响图7(a)、(b)、(c)分别对应3种不同粒径(1.3、2.4、3.5 mm)时石墨管中部各频段振动位移信号的标准偏差随蒸汽压力的变化规律。从图7可得，整体上看，颗粒的直径增大，低中频和高频振动位移信号的标准偏差稍有增加。粒径对振动行为的影响主要有两方面：一方面，在相同的固含率下，粒径的增加意味着颗粒数量的减小，进而会降低颗粒与管壁碰撞的频率，减弱振动；另一方面，粒径的增加，代表着颗粒动量的增加，会增加颗粒与管壁的碰撞力度，进而增强振动。综合两方面的共同影响，颗粒粒径对石墨管振动行为影响较小。

2.3.4轴向位置的影响图8是石墨管3个轴向位置处(测量点A、B、C)各频段信号的标准偏差随蒸汽压力的变化规律。不同高度的石墨管的振动行为主要受内部流体行为和石墨管连接方式两个因素的影响。原始振动信号的标准偏差由大到小依次为测量点B、A、C。由于石墨管两端固支(图1)，所以石墨管中间位置(测量点B)的振动行为强于两端(测量点A、C)。沿石墨换热管轴向方向从下到上，气泡逐渐形成，液固两相流动逐渐发展成汽液固三相沸腾流动。随着三相流体湍动程度的增加，流体激发的振动行为也逐渐增强，所以测量点A的标准偏差大于测量点C。但是下部区域的高频振动信号(测量点C)的标准偏差大于上部区域(测量点A)。原因是石墨管下部区域为液固两相区，颗粒浓度高于管上部的三相区，因此对应颗粒行为的高频振动强度较强。低频振动信号的轴向振动规律和原始信号相同。

2.4石墨管振动强度的关联式

基于安全性考虑，实验参数的测试范围有限，基本在正常的工业生产的操作范围。因此，建立振动强度的经验关联式可以为相似工况下的操作运行提供一定的参考。研究表明，石墨管振动行为主要与加热蒸汽压力、固含率、颗粒直径、液体和固体颗粒的物性有关。

图7　不同粒径情况下石墨管中部振动信号的标准偏差随蒸汽压力的变化规律Fig. 7　Variations of standard deviations of original vibration signals versus heating steam pressure at varied particle diameter and different solid holdups in measuring point B

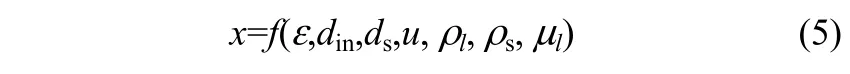
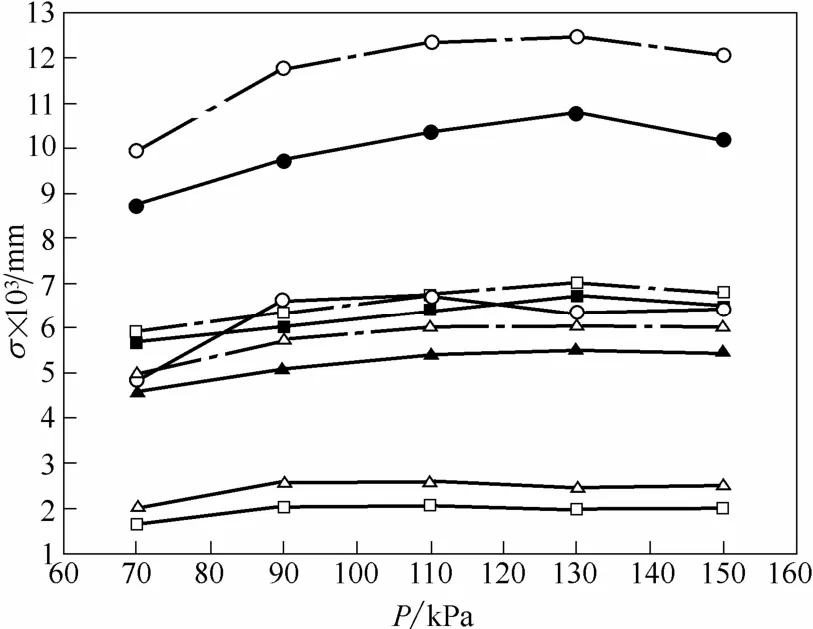
图8　石墨管不同位置处振动位移信号的标准偏差随蒸汽压力的变化规律Fig. 8　Variations of standard deviations of different kinds of vibration signals versus heating steam pressure at varied axialpositions when ε =1.0% and ds=2.4 mm

量纲1准数关联式形式简单、物理意义明确，在工程上得到了广泛应用。其中，振动位移对应于振动强度，颗粒直径对应于阿基米德数，加热蒸汽压力对应于表征流体流动状态的参量Reynolds数。最终得到以量纲1数群表示的振动强度的经验关联式如下。

汽液两相流动沸腾

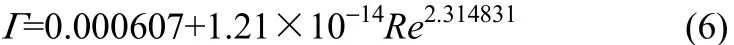
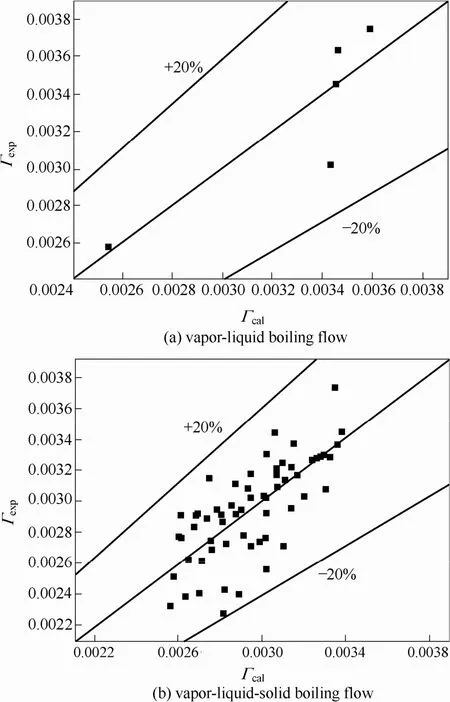
汽液固三相流动沸腾

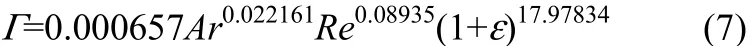
式中，din为石墨管内径, m; Ar为阿基米德数，; Re为Reynolds数，Γ为振动强度，; ds为颗粒直径, m; ρs为颗粒密度, kg·m−3; u为循环速度, m·s−1; x为振动位移, m。参数范围如下：0.002<Г<0.004, 0<ε<2%; 2.51×106< Ar <8×106, 2.95×105< Re <8.33×105，其中振动位移的范围为0.5×10−5m

图9是振动强度的实验值与关联式计算值的对比。两相系统的振动强度计算值与实验值的平均误差为4.99%，三相系统的是5.92%，表明振动位移关联式具有一定的预测性。

3　结　论

（1）通过单相常温液体静止、单相液体缓慢外部自然循环沸腾流动、汽液两相外部自然循环沸腾流动、汽液固三相外部自然循环沸腾流动条件下的振动位移信号的时间序列、功率谱图对比分析，揭示了振动位移信号的多尺度特性。宏观低中频成分(0～20 Hz)对应于流体和大气泡的行为，微观高频成分(20～100 Hz)对应颗粒的碰撞行为。

图9　汽液两相及汽液固三相流动沸腾系统石墨管振动强度计算值与实验值的比较Fig. 9　Comparisons between calculated and experimental values of vibration intensity of graphite tube with vapor-liquid and vapor-liquid-solid boiling flows

References

[1] RAUTENBACH R, ERDMANN C, ST KOLBACH J. Fluidized bed technique in the evaporation of wastewaters with severe fouling/scaling potential — latest developments, applications, limitations [J]. Desalination, 1991, 81(1/2/3): 285-298.

[2] KLAREN D G, DE BOER E F, SULLIVAN D W. “Zero fouling”self-cleaning heat exchanger [J]. Heat Transfer Engineering, 2007, 28 (3): 216-221.

[3] LIU M Y, YANG Y, LI X L, et al. Concentration of Gengnian’an extract with a vapor-liquid-solid evaporator [J]. AIChE Journal, 2005, 51(3): 759-765.

[4] 强爱红, 刘明言, 孙永利.汽液固三相流动沸腾传热系统的非线性特性 [J]. 化工学报, 2005, 56(5): 779-785. DOI: 0438-1157 (2005) 05-0779-07. QIANG A H, LIU M Y, SUN Y L. Nonlinear characteristics in vapor-liquid-solid flow boiling system [J]. Journal of Chemical Industry and Engineering (China), 2005, 56(5): 779-785. DOI: 0438-1157 (2005) 05-0779-07.

[5] BAGHERI F, FAKOOR-PAKDAMAN M, BAHRAMI M. Utilization of orthotropic graphite plates in plate heat exchangers, analytical modeling [J]. International Journal of Heat and Mass Transfer, 2014, 77: 301-310.

[6] HEMRICK J G, LARA-CURZIO E, LOVELAND E R, et al. Woven graphite fiber structures for use in ultra-light weight heat exchangers [J]. Carbon, 2011, 49(14): 4820-4829.

（2）借助于小波分解，从原始振动位移信号中提取了不同尺度的振动位移信号。其中，低中频振动信号 (LFS/MFS) 由子波a8、D8、D7叠加重建形成，高频振动信号 (HFS) 由子波D6～D1叠加重建形成。

（3）增加蒸汽压力，原始振动信号和小波分解得到的低中频振动信号的标准偏差先增加后稳定，高频振动信号的有微弱增加；颗粒的加入和流化会抑制管子的低中频振动行为，增强高频振动行为；增加固含率，原始振动信号的标准偏差增加，低中频振动信号相对稳定，高频振动信号明显增加；增加粒径，低中频和高频振动位移信号的标准偏差微弱增加。整体看来，粒径对振动位移行为影响有限。在石墨管不同轴向位置，原始振动信号和低频振动信号的标准偏差由大到小依次为中间，上部和下部，但下部区域的高频振动行为强于上部区域。

（4）对实验数据回归得到了两相外部自然循环沸腾流动和三相外部自然循环沸腾的振动强度的关联式。实验值和关联式计算值的对比分析表明，关联式预测准确性较高。

符号说明

ai——近似波，mm

Di——细节波，mm

din——石墨管内径，m

ds——颗粒直径，mm

f——频率，Hz

g——重力加速度，9.81 m·s−2

H——测量点距离石墨底端的距离，m

L——石墨管的长度，m

P——加热蒸汽压力，kPa

Pxx——估计功率谱，mm2·Hz−1

u——循环速度，m·s−1

x——振动位移信号时间序列

xi——振动位移信号的值，mm

Г——振动强度

ε——固含率

μl——液相黏度，Pa·s

ρl——液相密度，kg·m−3

ρs——颗粒密度，kg·m−3

σ——标准偏差

τH——延迟时间，s

[7] AZEVEDO C R F, ALVES G S. Failure analysis of a heat-exchanger serpentine [J]. Engineering Failure Analysis, 2005, 12(2): 193-200.

[8] VAN D A, HARRY E A. Toward a truly multiscale computational strategy for simulating turbulent two-phase flow process [J]. Industrial & Engineering Chemistry Research, 2010, 49(21): 10780-10797.

[9] LEE T H, ZHU C. Numerical simulation of evaporating crossflow sprays in gas-solids circulating fluidized beds [J]. Journal of the Chinese Institute of Chemical Engineers, 2005, 36(1): 43-48.

[10] TIJSSELING A S. Fluid-structure interaction in liquid-filled pipe systems: a review [J]. Journal of Fluids and Structures, 1996, 10(2): 109-146.

[11] 李公法, 孔建益, 侯宇, 等. 考虑液固耦合的输液管道振动模型研究 [J]. 机床与液压, 2010, 38(9): 15-17. LI G F, KONG J Y, HOU Y, et al. Research on vibration model of pipe conveying fluid considering fluid structure interaction[J]. Machine Tool & Hydraulics, 2010, 38(9): 15-17.

[12] 周晓军, 宫敬. 气液两相瞬变流的流固耦合模型研究 [J]. 力学与实践, 2003, 25: 17-20. ZHOU X J, GONG J. Fluid-structure interaction model for gas-liquid transient flows [J]. Mechanics in Engineering, 2003, 25: 17-20.

[13] SALEHI-NIK N, SOTUDEH-GHAREBAGH R, MOSTOUFI N, et al. Determination of hydrodynamic behavior of gas-solid fluidized beds using statistical analysis of acoustic emissions [J]. International Journal of Multiphase Flow, 2009, 35(11): 1011-1016.

[14] BRIENS L A, ELLIS N. Hydrodynamics of three-phase fluidized bed systems examined by statistical, fractal, chaos and wavelet analysis methods [J]. Chemical Engineering Science, 2005, 60(22): 6094-6106.

[15] AZIZPOUR H, SOTUDEH-GHAREBAGH R, ZARGHAMI R, et al. Characterization of gas-solid fluidized bed hydrodynamics by vibration signature analysis [J]. International Journal of Multiphase Flow, 2011, 37(7): 788-793.

[16] 张钦杰. 气液两相流管道振动机理研究[D]. 山东: 中国石油大学, 2009. ZHANG Q J. Research of vibration mechanism of pipeline conveying gas-liquid two-phase flow[D]. Shandong: China University of Petroleum, 2009.

[17] 白博峰, 郭烈锦, 赵亮. 垂直上升管汽液两相流型的压差波动特征识别 [J]. 化工学报, 1999, 50(6): 799-805. BAI B F, GUO L J, ZHAO L. Identification of flow regimes in vertical upward steam-water two phase flow using differential pressure fluctuations [J]. Journal of Chemical Industry and Engineering (China), 1999, 50(6): 799-805.

[18] 唐玥祺, 曹翌佳, 王靖岱, 等. 基于振动信号分析法的催化剂积炭量测量模型 [J]. 化工学报, 2011, 62(1): 78-84.DOI: 0438-1157 (2011) 01-0078-07. TANG Y Q, CAO Y J, WANG J D, et al. A model for determination of amount of coke deposit on catalyst based on vobration signal analysis [J]. CIESC Journal, 2011, 62(1): 78-84. DOI: 0438-1157 (2011) 01-0078-07.

[19] MALLAT S. A Wavelet Tour of Signal Processing [M]. Cambridge: Academic Press, 2009.

[20] REN J Q, MAO Q M, LI J H, et al. Wavelet analysis of dynamic behavior in fluidized beds [J]. Chemical Engineering Science, 2001, 56(3): 981-988.

[21] LIU M Y, QIANG A H, SUN Y L. Characteristics of flow and heat transfer in a tube bundle evaporator with a vapour-liquid-solid flow [J]. Chemical Engineering Research and Design, 2007, 85(A2): 256-262.

[22] 唐照千, 黄文虎. 振动与冲击手册——振动与冲击测试技术[M].北京: 国防工业出版社, 1990: 173. TANG Z Q, HUANG W H. Vibration and Shock Handbook-Vibration and Shock Testing Technology[M]. Beijing: National Defence Industry Press, 1990: 173.

[23] 李正周. 数字信号处理与应用[M]. 北京: 清华大学出版社, 2005: 156. LI Z Z. The Processing and Application of Digital Signal[M]. Beijing: Tsinghua University Press, 2005: 156.

[24] LIU M Y, SUN B F, LUO H,et al. Local flow and heat transfer behaviours in V-L-S fluidized bed evaporator [J]. Chemical Engineering Research and Design, 2007, 85(9): 1225-1244.

DOI：10.11949/j.issn.0438-1157.20151541

中图分类号：TQ 051.62; TH 145.1+2; TH 113.1

文献标志码：A

文章编号：0438—1157（2016）02—0530—10

基金项目：国家自然科学基金项目（21176176）。

Corresponding author:Prof. LIU Mingyan, myliu@tju.edu.cn supported by the National Natural Science Foundation of China (21176176).

Characteristics of vibration displacement signals of graphite tube in fluidized bed evaporator

AN Min1, LIU Mingyan1,2, XU Xiaoping1
(Collaborative Innovation Center of Chemical Science and Engineering (Tianjin), School of Chemical Engineering and Technology,
Tianjin University, Tianjin 300072, China;
2State Key Laboratory of Chemical Engineering (Tianjin University), Tianjin 300072, China)

Abstract:The characteristics of vibration displacement signals of graphite tube in vapor-liquid-solid (V-L-S) external circulating fluidized bed evaporator were investigated by means of accelerometers and a system of measurement and analysis of dynamic vibration signals using signal analysis tools of the standard deviation, power spectrum and wavelet transformation. Main results were as follows. The original and global vibration displacement signal with multi-scale behavior can be decomposed into low and middle vibration displacement signal (LFS/MFS) and high frequency vibration displacement signal (HFS). The standard deviation of the original signal (under V-L-S boiling flow) and its LFS/MFS by wavelet transformation increased at first and then a stable trend with increasing steam pressure, and its HFS by wavelet transformation showed a slight increasing trend. The addition of solid particles can weaken the vibration intensity of LFS/MFS and enhance the vibration intensity of HFS. The standard deviation of HFS represented an apparent increasing trend with the solid holdup. The standard deviation of three vibration signals (original, LFS/MFS, HFS) indicated a weak enhancement with solid particlediameter. The vibration behavior of graphite tube at different axial positions was also investigated. Two correlations of vibration intensity for vapor-liquid and V-L-S boiling flows were provided.

Key words:vapor-liquid-solid flow; graphite tube; evaporation; vibration displacement signal; multi-scale; safety