一种改进钟差二次多项式模型的导航卫星钟差预报方法∗

王宇谱吕志平 孙大双 王 宁

(1解放军信息工程大学地理空间信息学院郑州450001)(2地理信息工程国家重点实验室西安710054)

一种改进钟差二次多项式模型的导航卫星钟差预报方法∗

王宇谱1,2†吕志平1孙大双1王 宁1

(1解放军信息工程大学地理空间信息学院郑州450001)
(2地理信息工程国家重点实验室西安710054)

为了更好地反映钟差特性并提高其预报精度,建立一种能够同时考虑星载原子钟物理特性、钟差周期性变化与随机性变化特点的钟差预报模型.首先采用附有周期项的二次多项式模型进行拟合提取卫星钟差(Satellite Clock Bias,SCB)的趋势项与周期项,然后根据拟合残差的特点采用时间序列ARIMA(Auto-Regressive Integrated Moving Average)模型对残差进行建模;最后将两种模型的预报结果结合得到最终钟差预报值.使用IGS(International GNSS Service)精密钟差数据进行预报试验,将新方法与二次多项式模型、灰色模型及ARIMA模型进行对比,证明了新方法能够更高精度地预报卫星钟差,且可以一定程度上改善ARIMA存在模型识别与定阶不准的不足.

天体测量学:时间,方法:数据分析

1 引言

卫星导航系统中星载原子钟的钟差预报在优化导航电文中的钟差参数、满足实时动态精密单点定位的需求、提供卫星自主导航所需的先验信息等方面具有重要的作用[1].因此,针对卫星钟差预报,国内外学者进行了大量的研究,建立起了大量的钟差预报模型[2−7].但这些已有的预报模型主要是一些单一模型,而对于像卫星钟差这种异常复杂的非线性、非平稳随机序列很难使用单一的模型进行有效预报[8].

本文同时考虑星载原子钟的物理特性、周期性变化特点与随机变化部分,在钟差二次多项式附加周期项模型的基础上,采用时间序列ARIMA模型对卫星钟的随机项进行建模,得到一种更加完善的卫星钟差组合预报模型.该方法首先采用附有周期项的二次多项式模型进行拟合来提取卫星钟差的趋势项与周期项,然后对拟合残差进行一次差分,得到便于ARMA模型确定的平稳时间序列,进而完成残差预报;最后将附有周期项的二次多项式模型和ARIMA模型的预报结果结合得到最终钟差预报值.采用IGS提供的GPS精密钟差数据,将新方法与二次多项式(QP)模型[5]、灰色模型(GM(1,1))[6]及ARIMA模型[7]进行对比,证明了新方法能够更高精度地预报卫星钟差,而且可以一定程度上改善ARIMA存在模型识别与定阶不准的不足.

2 算法原理

根据星载原子钟的物理特性,在构造精密钟差模型时,通常采用包含表征卫星钟时频特性的相位(钟差)、频率(钟速)、频率漂移率(钟漂)的二次多项式模型,其具体表达式为[4]:

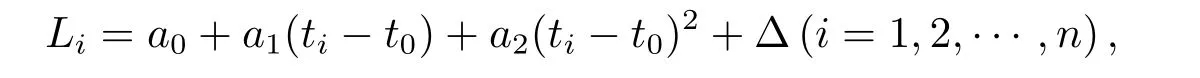
其中,Li是ti时刻的卫星钟差,t0为星历表参考时刻,ti表示历元时刻;待估参数a0、a1和a2分别表示参考时刻t0的相位、频率及频率漂移率;Δ为观测误差.当已知钟差数据不少于3个时,便可拟合求得待估参数.此外,在钟差的拟合预报中,除了以二次多项式来反映钟差的趋势项部分,还应考虑钟差的周期变化特性;附加周期项的二次多项式(MQP)模型表达式为[9]:

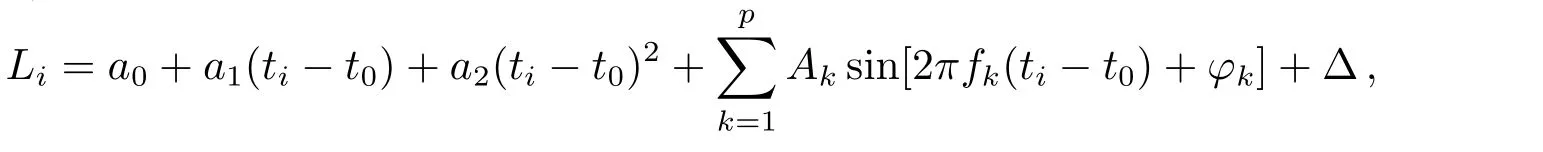
式中,p为主要周期函数的个数,Ak、fk、φk分别为对应周期项的振幅、频率和相位,其余符号的含义与二次多项式模型的表达式相同.p与fk的值可利用频谱分析来确定,而本文根据文献[10]的研究结果,直接取12 h、6 h作为主周期项.此外,为了更好地反映钟差特性并提高钟差预报精度,在考虑星载原子钟物理特性和周期变化特点的基础上,还应考虑其随机项部分[11].ARIMA模型是一种将自回归模型与滑动平均模型有机组合起来的高级预报方法,适合用来预报像钟差随机项这种随机时间序列.基于差分处理的ARIMA(p,d,q)模型,记为{xt}～ARIMA(p,d,q),其中{xt}是数据序列,p、q为模型的阶,d为差分的次数;当d为0时,ARIMA模型即为ARMA模型,定义为[7]:

式中,ai、bj为相应的待估参数,分别称为自回归参数和滑动平均参数;εt为白噪声序列.使用ARIMA模型进行钟差建模和预报时,模型及其阶数的合理确定是关键.本文首先根据自相关函数和偏相关函数的截尾性初步确定模型和模型的阶数,在模型确定以后,利用AIC(Akaike Information Criterion)准则来准确确定模型的阶数;模型及其阶数确定以后,通过已知数据使用较为常用的最小二乘估计方法来求解模型参数[12].最后,本文所建立的钟差预报模型的表达式可以写为:

式中各参数的含义与前面提到的参数一样,需要说明的是式中的时间参数ti和t0均以秒为单位.新方法的工作原理如图1所示.

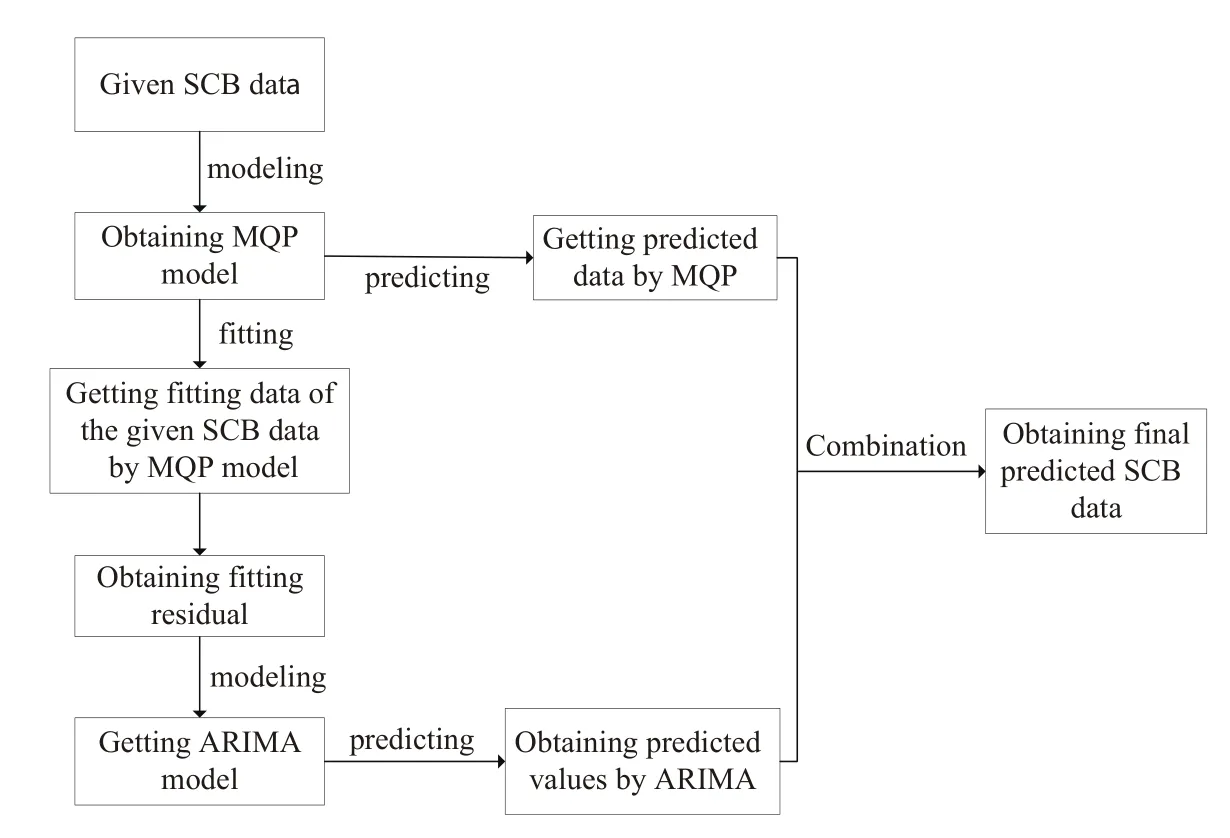
图1 新方法的钟差预报原理Fig.1 SCB prediction principle of the proposed method

3 试验与分析

为了验证所提方法(QARIMA模型)的有效性,采用IGS提供的GPS系统15 min采样间隔的精密钟差数据进行试算分析.以2012年9月19号到2012年9月25号的数据为例,考虑当前在轨运行的GNSS(Global Navigation Satellite System)星载原子钟主要是铷原子钟(Rb钟),而该时间段内GPS星载Rb钟包含4种类型:BLOCK IIA Rb钟、IIR Rb钟、IIR-M Rb钟及IIF Rb钟,随机选取该时间段内数据完整的每种类型钟对应的1颗卫星,本文选取的是PRN01、PRN17、PRN21和PRN26 4颗卫星进行预报试验.另外,以预报时间段对应的已知精密钟差值为基准值,采用均方根误差(RMS)和极差(最大、最小误差之差的绝对值,记作Range)作为预报结果的统计量进行对比与分析,其中RMS表征预报结果的精度,Range代表预报结果的稳定性.

3.1 试验一

首先分析新方法的建模过程及其预报特性.以PRN17卫星为例,采用MQP模型对9月19号的钟差数据进行拟合,图2为其钟差的拟合残差.从该图可以看出,拟合残差仍呈现出一定的变化趋势,这将不利于ARMA建模.对残差进行一次差分后(如图3)可以看出变化趋势得到较好的消除.其他卫星类似,通过对拟合残差进行一次差分方便对ARMA建模.

在此分析基础上,4颗卫星使用各自对应9月19号的精密钟差数据,分别对QP、MQP和QARIMA进行建模,预报9月20号一整天的钟差.表1给出4颗卫星拟合残差进行ARIMA建模时p,d,q的取值情况.图4～7为4颗卫星在3种模型下的预报结果.对比图中4颗卫星在3种模型下的预报结果看出,本文所提的QARIMA模型预报误差比QP模型与MQP模型预报误差小且发散慢,说明考虑钟差随机项并使用ARIMA对其进行建模是合理的.为了对预报结果进行定性分析,表2给出了4颗卫星预报结果的统计值.

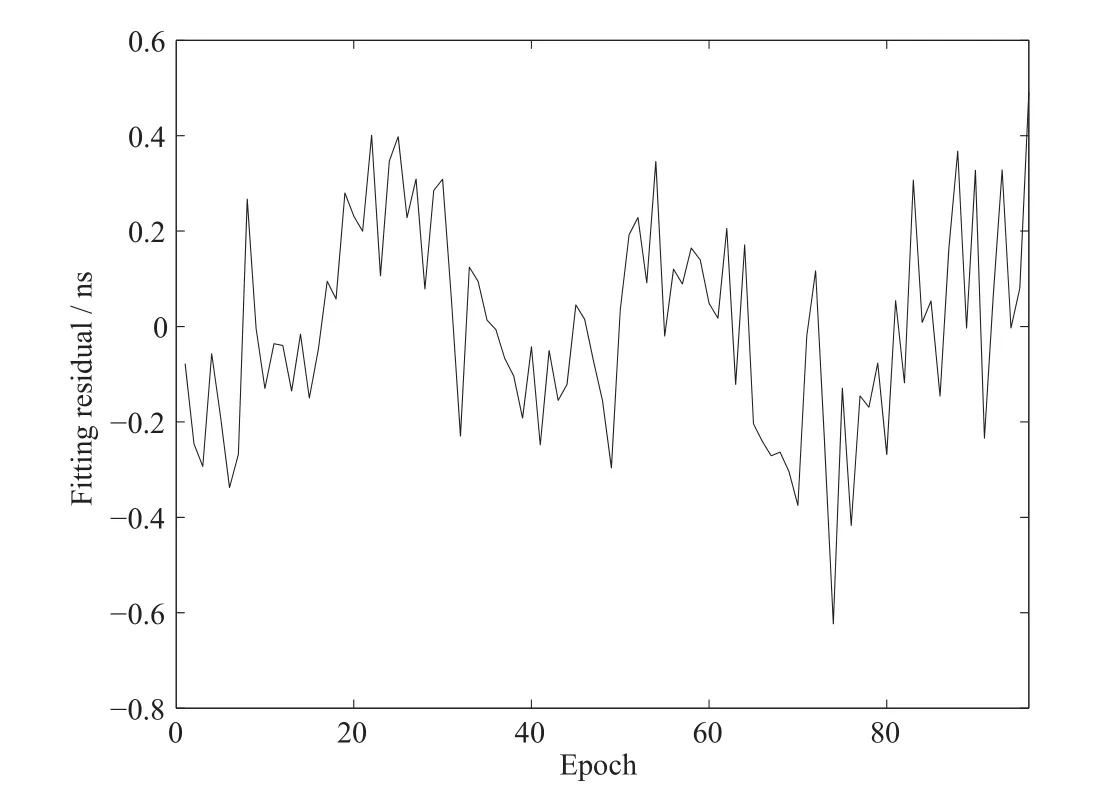
图2 PRN17卫星的钟差拟合残差Fig.2 SCB fitting residual of satellite PRN17

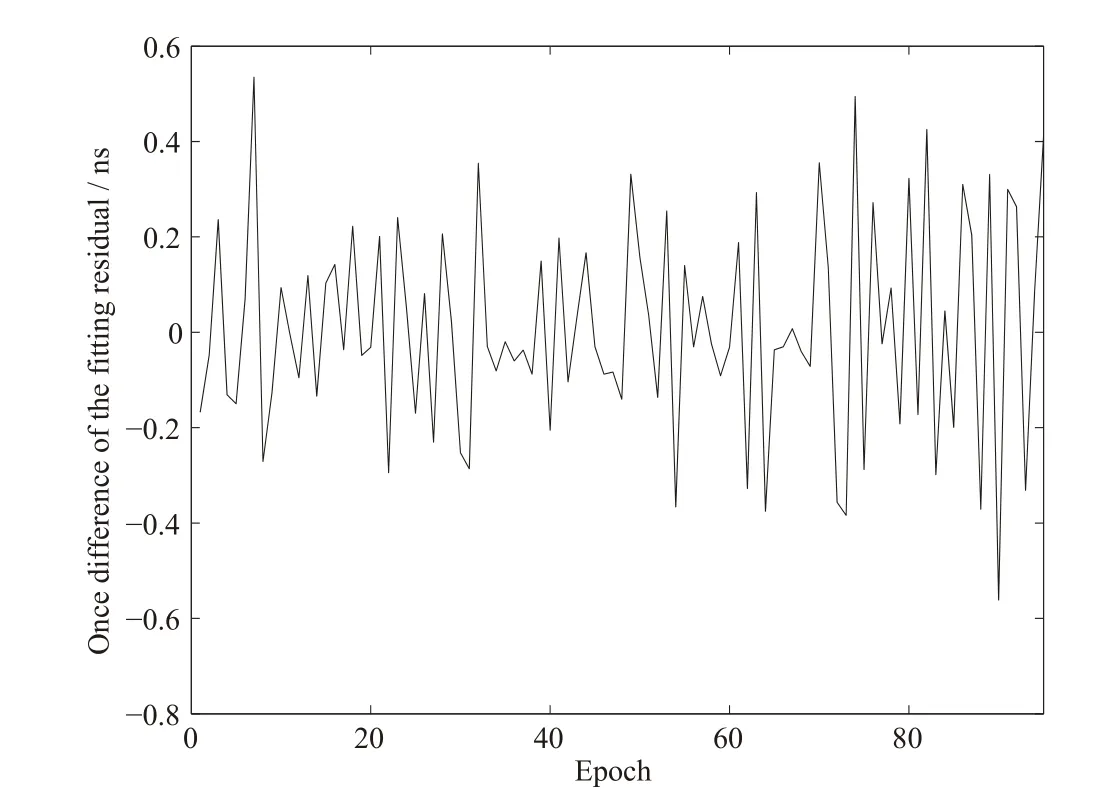
图3 PRN17卫星的钟差拟合残差一次差序列Fig.3 Once di ff erence series of the SCB fitting residual of satellite PRN17

表1 4颗卫星在ARIMA模型中参数的取值Table 1 Parameters’values for the ARIMA models of four satellites

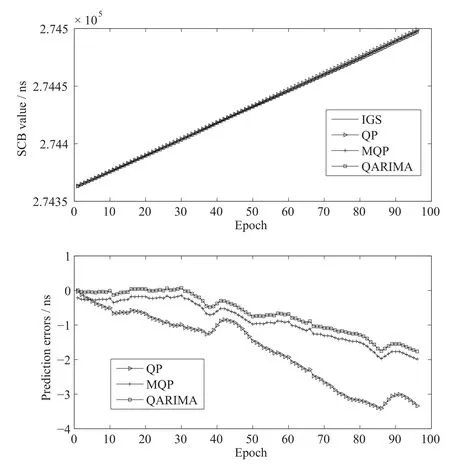
图4 PRN01卫星的预报结果Fig.4 Prediction results of satellite PRN01

图5 PRN17卫星的预报结果Fig.5 Prediction results of satellite PRN17

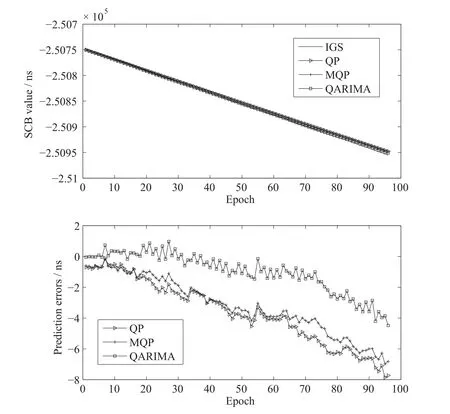
图6 PRN21卫星的预报结果Fig.6 Prediction results of satellite PRN21

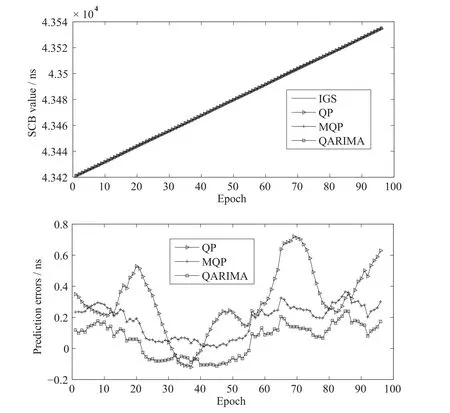
图7 PRN26卫星的预报结果Fig.7 Prediction results of satellite PRN26

表2 4颗卫星预报结果的统计值(单位:ns)Table 2 Statistics of prediction results from four satellites(unit:ns)

从该试验预报结果统计表中可以看出,每颗卫星的预报结果中QARIMA模型的RMS值与Range值最小,其次是MQP模型,而QP模型的统计值最大;说明本文所建模型的预报精度与预报稳定性最好,该模型能够在钟差物理特性和周期特性的基础上考虑钟差的随机项得到更加完善的钟差模型.根据4颗卫星预报结果的平均值可知,精度方面新模型比常用的QP模型提高2倍多,而新模型预报结果的稳定性也有较大程度的改善.

3.2 试验二

将本文所提方法与常用的QP模型、GM(1,1)模型及ARIMA模型进行对比,进一步分析新方法较3种常用模型的预报特性.采用9月24号4颗卫星一整天的钟差数据进行建模,预报接下来9月25号一整天的钟差;而其中GM(1,1)的建模方案类似于文献[6],即使用9月24号最后2 h的钟差数据进行建模.表3给出了本试验中单一ARIMA模型及新方法中ARIMA对应的参数取值.图8～11是4颗卫星在各模型下的预报误差.从图中可以看出,本文所提方法的预报误差相对较小且发散较慢,同时误差的波动范围也较小,因此说明新方法的预报效果优于其他3种模型.表4为本试验下4颗卫星预报结果的统计情况.

表3 2种模型下对应ARIMA参数的取值Table 3Parameters’values of the ARIMA models corresponding to the two models

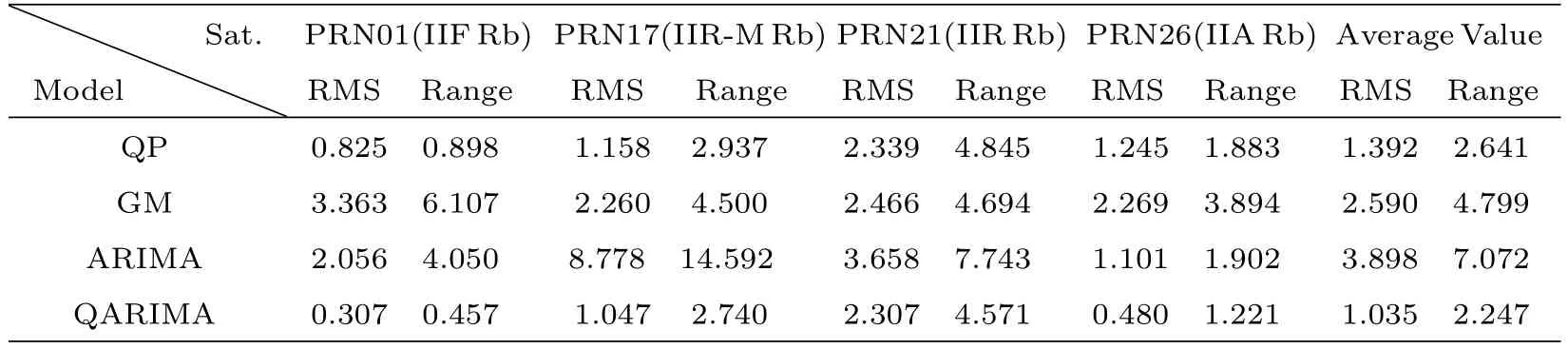
表4 4颗卫星预报结果的统计值(单位:ns)Table 4 Statistics of prediction results from four satellites(unit:ns)

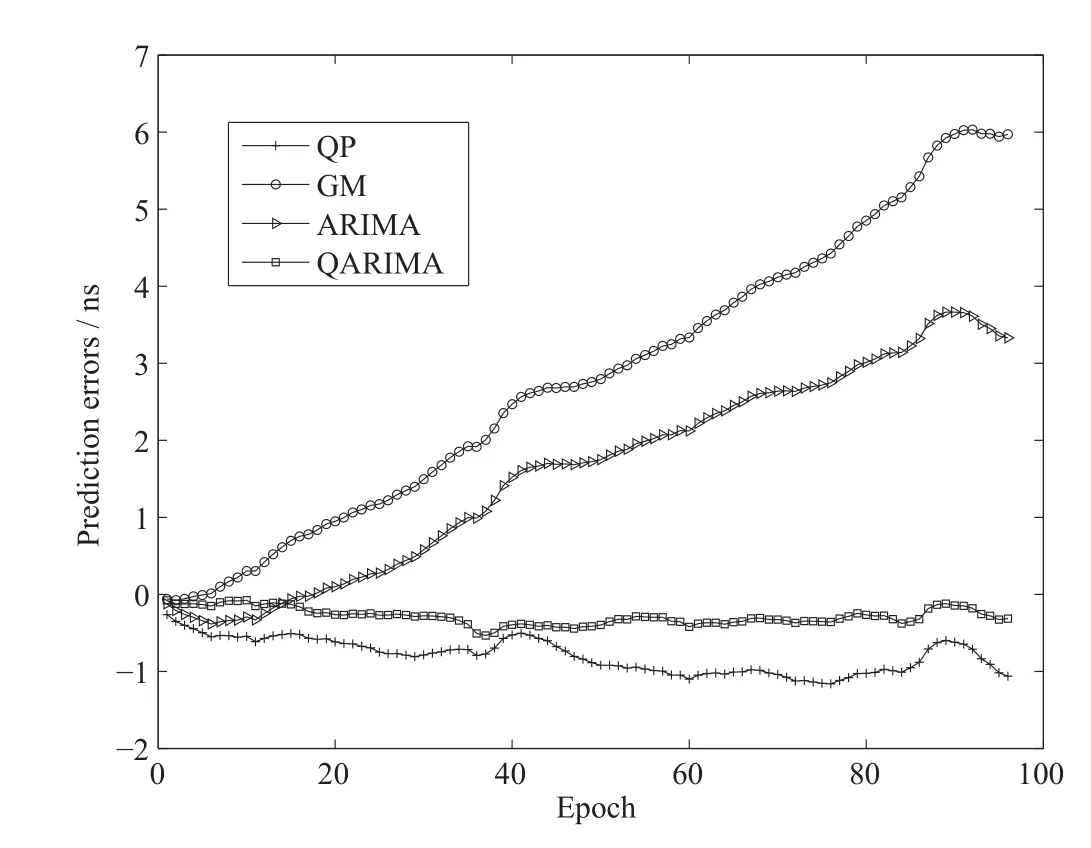
图8 PRN01卫星的预报误差Fig.8 Prediction errors of satellite PRN01

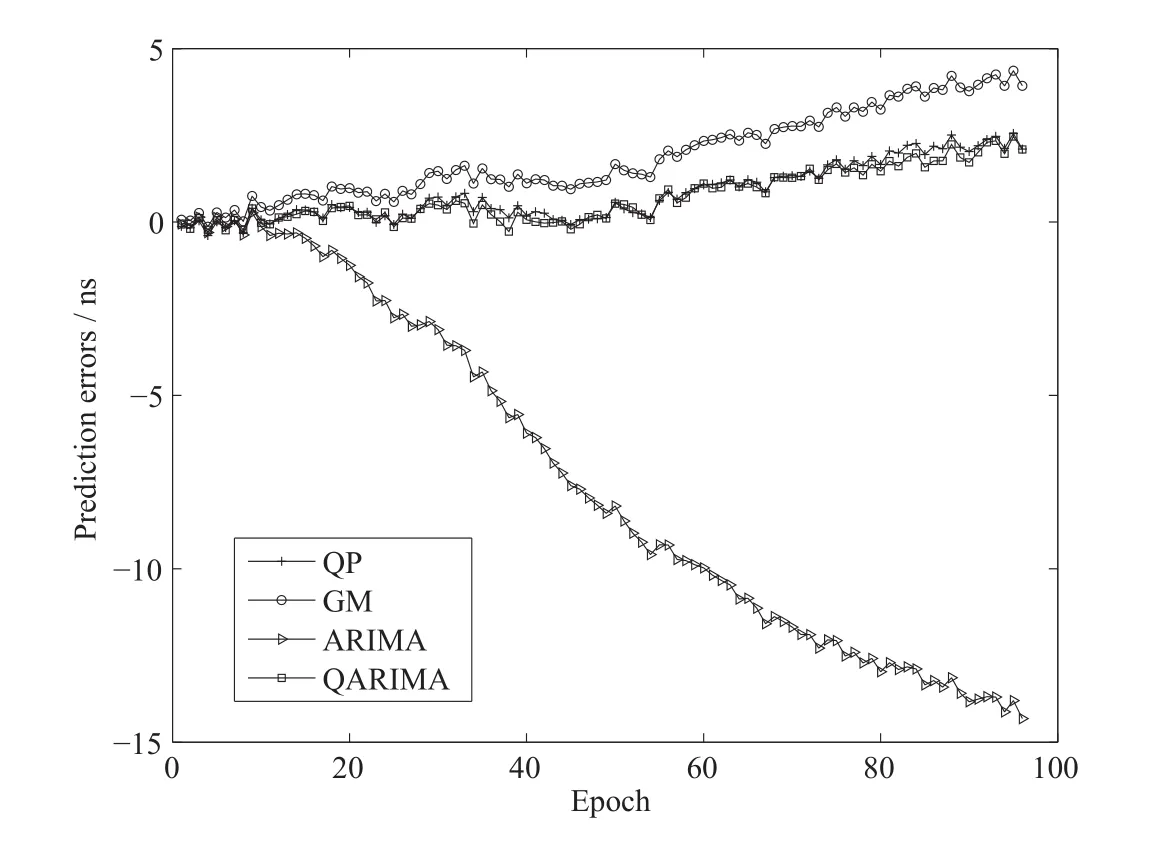
图9 PRN17卫星的预报误差Fig.9 Prediction errors of satellite PRN17

图10 PRN21卫星的预报误差Fig.10 Prediction errors of satellite PRN21

图11 PRN26卫星的预报误差Fig.11 Prediction errors of satellite PRN26

根据表4的统计结果可知,不论是单颗卫星的预报结果还是4颗卫星预报结果的平均值,在预报精度(RMS值)与预报稳定性(Range)上,本文所提方法均优于其他3种模型,进一步说明本文所提方法的有效性以及采用ARIMA模型对钟差随机项建模的正确性.对比4颗卫星预报结果的平均值可以看出,在钟差建模数据一定的条件下,QP模型与GM(1,1)模型的钟差预报效果优于ARIMA模型,这是由于ARIMA模型在建模数据较少时存在着模型识别与定阶不准的不足;同时从表中ARIMA模型与新方法QARIMA的预报结果可知,采用组合预报的方法比单纯使用ARIMA模型进行钟差预报时的预报效果要好;因此可以说明,采用本文所提方法进行钟差预报,不但可以在钟差物理特性与周期特性的基础上考虑钟差的随机特性,而且能够一定程度上改善单独使用ARIMA模型进行钟差预报时存在的不足.另外,新方法较3种传统方法的优效性说明考虑钟差的随机项可以进一步提高钟差预报的效果.

4 总结

为了改进钟差预报模型、提高钟差预报精度,本文在钟差二次多项式模型的基础上顾及了钟差的主要周期项并将钟差的随机项部分考虑到钟差预报建模中,建立了一种更加完善的钟差预报模型.通过钟差预报试验得到了以下结论:

(1)在卫星钟差预报中,顾及钟差的周期特性与随机项部分能够进一步提高钟差预报的效果;

(2)采用ARIMA模型对钟差随机项进行建模是合适的,同时基于附加周期项的二次多项式模型与ARIMA模型的组合钟差预报模型,能够一定程度上克服单独使用ARIMA模型进行钟差预报时的不足,并且取得较ARIMA模型更好的预报效果;

(3)本文所提方法能够有效地进行钟差预报且预报效果优于常用的QP模型和GM(1,1)模型.

[1]王宇谱,吕志平,陈正生,等.测绘学报,2013,42:323

[2]Heo Y J,Cho J,Heo M B.MeScT,2010,21:073001

[3]Davis J,Bhattarai S,Ziebart M.Development of a Kalman Filter Based GPS Satellite Clock Timeo ff set Prediction Algorithm.Gothenburg:European Frequency and Time Forum(EFTF),2012

[4]Huang G W,Zhang Q,Xu G C.GPS Solutions,2014,18:95

[5]郑作亚,党亚民,卢秀山,等.天文学报,2010,51:95

[6]崔先强,焦文海.武汉大学学报:信息科学版,2005,30:447

[7]徐君毅,曾安敏.大地测量与地球动力学,2009,29:116

[8]雷雨,赵丹宁.天文学报,2014,55:216

[9]郭海荣.导航卫星原子钟时频特性分析理论与方法研究.郑州:信息工程大学,2006:143-150

[10]Senior K L,Ray J R,Beard R L.GPS Solutions,2008,12:211

[11]Lei Y,Zhao D N,Hu Z P,et al.China Satellite Navigation Conference(CSNC)2015 Proceedings: Volume III.Berlin and Heidelberg:Springer-Verlag,2015:411-423

[12]王宇谱,吕志平,宫晓春,等.大地测量与地球动力学,2015,35:373

A New Navigation Satellite Clock Bias Prediction Method Based on Modi fied Clock-bias Quadratic Polynomial Model

WANG Yu-pu1,2LV Zhi-ping1SUN Da-shuang1WANG Ning1
(1 School of Surveying and Mapping,The PLA Information Engineering University, Zhengzhou 450001)
(2 State Key Laboratory of Geo-information Engineering,Xi’an 710054)

In order to better express the characteristics of satellite clock bias(SCB) and improve SCB prediction precision,this paper proposed a new SCB prediction model which can take physical characteristics of space-borne atomic clock,the cyclic variation, and random part of SCB into consideration.First,the new model employs a quadratic polynomial model with periodic items to fit and extract the trend term and cyclic term of SCB;then based on the characteristics of fitting residuals,a time series ARIMA (Auto-Regressive Integrated Moving Average)model is used to model the residuals; eventually,the results from the two models are combined to obtain final SCB prediction values.At last,this paper uses precise SCB data from IGS(International GNSS Service) to conduct prediction tests,and the results show that the proposed model is effective and has better prediction performance compared with the quadratic polynomial model, grey model,and ARIMA model.In addition,the new method can also overcome the insufficiency of the ARIMA model in model recognition and order determination.

astrometry:time,methods:data analysis

P127;

:A

10.15940/j.cnki.0001-5245.2016.01.008

2015-05-26收到原稿,2015-06-10收到修改稿

∗国家自然科学基金项目(41274015)、国家863计划项目(2013AA122501)、地理信息工程国家重点实验室开放研究基金资助项目(SKLGIE2015-M-1-6)资助

†987834660@qq.com