钢筋混凝土梁疲劳累积损伤过程的等效静力分析方法

王青，卫军，刘晓春，徐港(1.中南大学 土木工程学院，湖南 长沙，410075；.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌，44300；3.高速铁路建造技术国家工程实验室，湖南 长沙，410075)



钢筋混凝土梁疲劳累积损伤过程的等效静力分析方法

王青1,2,3，卫军1,3，刘晓春1,3，徐港2
(1.中南大学 土木工程学院，湖南 长沙，410075；2.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北 宜昌，443002；3.高速铁路建造技术国家工程实验室，湖南 长沙，410075)

摘要：为了实现对钢筋混凝土梁疲劳性能的全过程分析和剩余承载力评估，提出一种混凝土构件疲劳累积损伤过程的等效静力分析方法。通过对材料疲劳刚度、强度退化和疲劳残余变形累积发展规律进行分析研究，建立混凝土和钢筋任意加载次数后的疲劳本构模型；基于混凝土材料在静态荷载与疲劳荷载作用下破坏的相似性，构建疲劳荷载与静载作用的等效关系，提出钢筋混凝土构件疲劳性能的等效静力分析方法。采用该方法对某混凝土试验梁进行疲劳性能分析。研究结果表明：所获得的数值模拟结果与实验值变化规律一致，吻合程度良好，验证了该方法的有效性和实用性。

关键词：钢筋混凝土；疲劳本构模型；等效静力分析；数值模拟

混凝土梁承受重复荷载作用将引起疲劳损伤，对其使用寿命和安全性都会产生严重影响。长期以来，人们主要通过室内疲劳试验，对混凝土梁的疲劳性能进行研究，但疲劳试验非常耗资费时，且不易进行足尺构件试验，尺寸效应难以克服，同时也难以模拟结构实际所经历的疲劳作用。近年来，随着数值仿真技术的发展，结构疲劳数值模拟的方法逐渐为研究者所采用。利用现有的疲劳分析软件虽然可以较好地预测结构的疲劳寿命，但仍无法对结构疲劳一定次数后的力学性能作出评判，更无法进行疲劳全过程分析。一些学者采用有限单元法(或条带法)对混凝土构件的疲劳损伤过程进行了仿真分析[1−3]，有些还对高周疲劳工况下的加载次数按照一定原则进行了简化，大大降低了计算工作量，但通常疲劳残余应变的累积、叠加和平衡迭代需通过编写专用程序或软件二次开发实现，通用性不强。为此，本文作者在对材料疲劳刚度、强度退化和疲劳残余变形累积发展规律进行分析总结的基础上，基于“变形唯一性”假定和混凝土材料在静态荷载与疲劳荷载作用下破坏的相似性，以残余应变作为等效参量，建立疲劳荷载与静载分析的等效关系，由1次静力加卸载构造出与疲劳N次损伤等效的状态梁，进而引入材料的疲劳损伤本构模型，建立构件受疲劳荷载作用的等效静力分析方法，基于ABAQUS有限元软件平台高效地实现高周疲劳荷载作用下钢筋混凝土梁的疲劳累计损伤过程分析和剩余承载力预测。

1　疲劳本构模型

1.1混凝土疲劳本构模型

1.1.1疲劳损伤后的应力−应变关系

混凝土在重复加卸荷作用下，疲劳损伤引起混凝土材性的退化主要表现为混凝土残余静强度和峰值应变降低、混凝土刚度衰减和残余变形增加[4]。以混凝土静力条件下的单轴受压本构模型[5]为基础，综合考虑混凝土疲劳刚度退化、疲劳强度退化和疲劳残余应变的演化规律，并忽略疲劳加载过程中卸载与再加载曲线之间可能存在的滞回现象，可通过试验回归法构建混凝土任意疲劳加载次数后的受压本构模型：

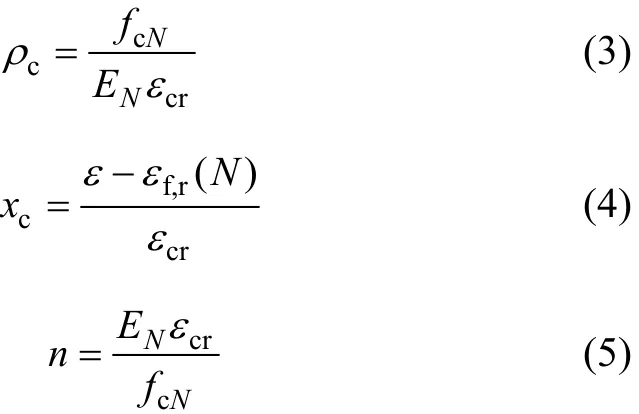
同理，可基于规范中单轴受拉的应力应变关系构建出N次疲劳后混凝土受拉本构模型：

式中：σ 和ε 分别为受压(拉)混凝土应力和应变；kc和kt分别为受压和受拉疲劳损伤演化的参数；αc和 αt为疲劳后应力应变曲线中下降段的形状参数，假定下降段曲线与静载应力应变曲线的下降段有相同的形状参数[5]，可参考文献[6]中表C.2.4 取值；εf,r(N)为第 N次加卸载后的残余应变；EN为疲劳N次后退化了的混凝土弹性模量；fcN，ftN，εcr和 εtr分别为疲劳 N 次后混凝土的剩余抗压、抗拉疲劳强度和第N次加载的峰值压应变、峰值拉应变，这些参数的确定是进行疲劳分析的关键，具体确定方法如下。

1.1.2疲劳残余应变

随着疲劳荷载次数增加，混凝土残余应变不断增加，且其值与疲劳荷载次数、应力水平等有关。现有的疲劳残余变形模型较多,主要可以分为：考虑应力比的疲劳残余变形模型和不考虑应力比的疲劳残余变形模型，相关参数可由试验回归分析得到。在没有更多试验数据供分析的情况下，采用下列不考虑应力比的公式计算疲劳加卸载N次后混凝土受压的纵向残余变形εf,r(N)[3]：

式中：εcr,1为第1次应力循环所引起的残余变形；εc,min和εc,max分别为荷载下限、 荷载上限作用下的初始瞬时应变；εunstab为疲劳变形第3阶段开始时混凝土的纵向总变形，取决于混凝土本身材料的性质，常取为1次加载破坏时的峰值应力所对应的应变ε0。

1.1.3刚度退化

混凝土弹性模量的退化是衡量构件刚度退化的重要指标。试验研究发现，混凝土疲劳弹性模量的变化随加载次数增加呈 3个阶段：第1阶段，弹性模量衰减较快；第2阶段，弹性模量呈稳定线性退化，该阶段疲劳应力占总疲劳寿命的75%～80%；第3阶段，弹性模量急剧不稳定衰减，直至疲劳破坏[7]。文献[8]通过大量的试验研究，得到第2阶段混凝土弹性模量与疲劳次数间满足如下关系：

其中：E0为混凝土初始弹性模量；EN为疲劳N次后的混凝土弹性模量；Nf为疲劳寿命[9],按照文献[11]取值；σmin和 σmax分别为荷载下限、荷载上限作用下的初始瞬时应力；fcu为混凝土的立方体抗压强度。

1.1.4强度退化

通过试验研究发现：对于某一给定的循环次数，疲劳强度不仅取决于循环中的最大应力，而且取决于最小应力。根据文献[10]的研究结果，混凝土受压疲劳次数 N 与压应力上限 σc,max(即剩余疲劳抗压强度fcN)以及压应力下限 σc,min的关系可表述成如下形式：

式中：β 为混凝土的材料常数，取值范围为 0.064～ 0.080，一般通过试验回归分析得到，在没有充足实验数据的情况下，可取为平均值0.072。混凝土受拉疲劳次数N与拉应力上限σt,max(即剩余疲劳抗拉强度ftN)以及拉应力下限σt，mi n的关系可表述成如下形式[10]：

式中：ft为混凝土的静态抗拉强度。确定fcN和ftN后，据规范表C.2.4[5]即可求得相应疲劳次数作用后的混凝土峰值压应变εcr和峰值拉应变εtr。

1.2钢筋的疲劳本构模型

钢筋高周疲劳的应力水平通常较低，未达到屈服强度，受力和变形基本处于弹性阶段，因此，一般认为钢筋弹性模量在整个疲劳加载过程中不发生退化，残余应变可以忽略。考虑到钢筋疲劳破坏是由于剩余有效承载面积不能承担拉伸荷载而产生的瞬态断裂，因此，常通过减小横截面积研究钢筋抗力性能随疲劳次数的降低规律。文献[11]根据 Miner 线性累积损伤准则，得到疲劳 N 次后钢筋的有效截面积可由下式计算：

式中：As为钢筋的初始横截面积；fy为普通钢筋的屈服强度(或预应力钢筋的极限抗拉强度)；σs,max为疲劳加载过程中钢筋的应力最大值。

假定钢筋在 N 次重复应力作用后发生了疲劳破坏，则钢筋在疲劳破坏时应满足下式：

将式(15)代入式(16)，可将有效面积换算为钢筋的等效剩余疲劳强度fs,N。基于钢筋的理想弹塑性模型，认为等效剩余屈服强度 fy,N与等效剩余疲劳强度 fs,max相等，即

2　混凝土结构疲劳加载与静载的等效损伤状态

疲劳加载次数通常是上百万次，若逐步计算则工作量巨大。众多研究成果表明：混凝土材料无论在静态荷载还是疲劳荷载作用下，其破坏过程均是裂缝在界面过渡区和基体中演化、发展的过程[12]。若能利用混凝土材料在静载与疲劳荷载作用下破坏的相似性，依据某等效参量建立疲劳荷载与静载分析的等效关系，则可由1次静力加卸载构造出与疲劳N次损伤等效的状态梁，进而引入材料的疲劳本构模型，实现对疲劳N次后结构受力性能的数值分析。若取不同的疲劳次数Ni进行等效静力分析，则可以得到任意疲劳次数后混凝土结构的裂缝、损伤、变形、应变、应力等的发展情况，由此实现高周疲劳荷载作用下钢筋混凝土梁的全过程分析。

2.1等效参量的选择

混凝土变形唯一性假设是 SINHA 等[13]提出的。该假设认为不管以前承受的重复荷载历程如何，只要残余变形相同，则在此基础上施加相同的重复荷载，其荷载与变形的关系将保持不变，而与以前的荷载变形历程无关。这一假设目前已被许多试验所证实。文献[6,14]的研究也认为，残余应变反映了混凝土的微塑性变形和微裂纹不可恢复程度，所以，比其他参数更能反映材料本身的损伤特性。为此，本文进行如下假定：设经过1次静力加载P1(P1＞Pmax)并卸载后的混凝土梁为状态1，受压边缘混凝土残余压应变为 εr；经历N次Pmin～Pmax疲劳荷载作用并卸载后的同一混凝土梁为状态2，受压边缘混凝土残余压应变为εf,r(见图1)；若二者的残余应变相等即 εr＝εf,r，则可认为经历了1次静力加卸载路径A的状态1混凝土和经历了疲劳加卸载路径B的状态2混凝土的能量耗散相同，损伤等效。

图1　等效状态示意图Fig.1　Diagram of equivalent state

若不考虑钢筋、混凝土之间的黏结性能退化及其相对滑移，则钢筋应变与该位置的混凝土应变相等，状态1与状态2的钢筋应变相等，应力相同，受力状态等效。为此，以混凝土受压区残余应变作为等效参量建立疲劳加载与静力加载的等效损伤状态，将经历了N次Pmin～Pmax疲劳加卸载的状态1梁等效为1次性静力加载至P1后卸载的状态2梁，并在此基础上进行钢筋混凝土梁疲劳加载后的受力分析。若根据各阶段特点取不同的疲劳次数Ni进行等效静力分析，则可以得到任意疲劳次数后混凝土结构的裂缝、损伤、变形、应变、应力等的发展情况，由此实现高周疲劳荷载作用下钢筋混凝土梁的全过程分析。

2.2静力加载中残余应变的计算模型及其等效状态的构建

由图1可知，静力加载中混凝土残余应变 εr可由下式求得：

式中：ε，εe和εr分别为加载至任意一点的混凝土总应变、弹性应变和残余塑形应变；E为加载至任一点的混凝土卸载弹性模量(如图1所示)；E0为初始弹性模量；d 为损伤因子，由加卸载试验确定，如缺少试验数据，也可应用能量等效原理，由

计算[15]。综上可知：基于前述疲劳损伤后的混凝土应力−应变关系，由式(18)～(20)可求得静力加载至任意一点的混凝土残余塑性变形 εr，再结合式(10)，令εf,r(N)=εr，即可由残余应变建立与疲劳加载路径 B 等效的1次静力加卸载路径A。

3　材料的疲劳失效准则

3.1混凝土的疲劳失效准则

在疲劳荷载作用下，混凝土内部的原始缺陷不断扩展。相关研究[14]表明：当疲劳后残余应变 εf,r达到0.4 倍的静载极限压应变 ε0(ε0为混凝土静载极限强度fc对应的应变)时，混凝土已经有很严重的损伤，不能再继续工作，就认为混凝土发生疲劳破坏，即混凝土在疲劳荷载作用下的疲劳失效准则为

令 εf,r(N)=εr，则可得到等效至静力加载中的混凝土疲劳失效准则：

3.2钢筋的疲劳失效准则

钢筋是以脆性断裂为疲劳破坏的标志，一般是以钢筋应力幅值是否超过疲劳破坏的允许应力幅值作为钢筋疲劳破坏依据。如对于HRB400钢筋，可参考文献[11]中的S−N方程确定。

4 疲劳荷载作用下的结构分析过程

基于前述计算模型和有限元分析方法，N 次疲劳后的结构受力性能分析流程如图2所示。若需要对疲劳过程中结构的各部分应力、应变、变形等进行全过程跟踪分析，则可根据各阶段特点取不同的疲劳次数Ni按照上述流程进行数值模拟计算，以得到任意疲劳次数后混凝土结构的应变、应力、变形情况，也可根据ABAQUS软件处理的损伤场(即损伤因子)分布推得结构中的裂缝发展趋势。

图2疲劳后力学性能的等效静力分析方法流程图Fig.2Flow-process diagram of equivalent static analysis method on fatigue behavior

5 算例验证

文献[16]进行了钢筋混凝土简支梁疲劳性能试验研究。以其中B40系列试验梁为例，该梁混凝土强度等级为C40，弹性模量为3.82×104MPa，几何尺寸及配筋如图3所示。

基于前述分析步骤采用 ABAQUS 软件进行数值分析。仿真模型中混凝土与钢筋分别选用C3D8R 和T3D2 单元模拟，采用 Embeded 技术模拟钢筋与混凝土的黏结，并在支座及加载位置设置刚垫片以防止应力集中导致局部破坏。

对B40组梁进行疲劳前的静载模拟分析，所得荷载−跨中挠度曲线如图4所示，可见模拟结果与静载试验曲线基本一致，说明本文对静载阶段的模拟方法和所选参数合理。

建立B40-2梁疲劳加载30万次的静力等效状态，试算时，等效静载 P1取190 kN，按照该等效静载进行1次加卸载后，将材料特性修改至疲劳30万次后的本构模型并进行静力加载，荷载−挠度曲线如图5所示。同理可得B40-1梁疲劳30万次后和疲劳100万次后的荷载−挠度模拟曲线，如图6所示。

在进行疲劳后梁的静载试验时，位移计已经重新归零，所测挠度均是去掉残余挠度之后的新增挠度。因此，图5和图 6中数值分析挠度计算结果也采用总挠度与残余挠度之差，以便于与试验结果进行对比。

从图5和图6 可以看出：疲劳加载后的静载模拟荷载−跨中挠度曲线与相应的试验曲线符合程度良好，相对误差一般在10%以内，且疲劳损伤对结构刚度的影响特征、趋势与试验结果相近，即疲劳加载前静载模拟时荷载挠度曲线在结构开裂点处有一转折点，说明混凝土开裂后截面发生应力重分布，裂缝处的混凝土工作，结构刚度显著减小；而经历了一定疲劳次数(30 万次、100 万次)后再加静载时的荷载挠度曲线近似为1条直线，这是因为经历了一定次数疲劳加载后，混凝土结构上的裂缝数量已基本稳定，不再有明显的应力重分布过程，使得截面表现出由弹塑性向弹性转变的规律；疲劳100万次比疲劳30万次的荷载挠度曲线斜率略下降，但是并不显著，说明疲劳30万次后结构刚度已经趋于稳定。这均与相关文献[11]中的研究结果相符。

图3　试验梁的配筋图Fig.3　Details of RC beam

为了得到疲劳荷载作用下受压区混凝土应变的发展过程，分别取Ni为20万、40万、60万、80万、100万次，对钢筋混凝土梁 B40-2 进行不同疲劳次数后的等效静力分析，可以得到相应的受压区混凝土应变εmin和εmax，如图7所示，与实验值进行对比符合度较高。受压区混凝土应变随着疲劳次数 N 的增大而逐渐增大，但增大的趋势在40万次以后逐渐减缓，这与混凝土疲劳发展的“三阶段变形规律”相符，说明疲劳至40万次后混凝土疲劳变形逐渐从第1阶段向第2阶段过渡。为了对疲劳加载过程中的裂缝发展进行跟踪分析，分别取Ni为5 000，20万和100万次，对钢筋混凝土梁 B40-2 进行相应的等效静力分析，并绘出不同Ni后，在荷载上限Pmax作用下的损伤因子分布云图，如图8所示。

图4静载下的荷载−跨中挠度曲线Fig.4Load−deflectionCurves under static load

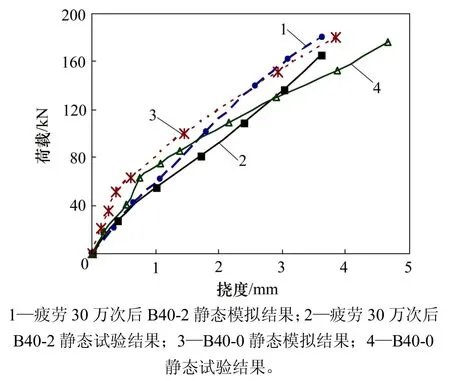
图5　B40-0静载分析和B40-2疲劳分析的荷载−跨中挠度曲线Fig.5　Load−deflectionCurves of static analysis and fatigue analysis for B40-0 and B40-2

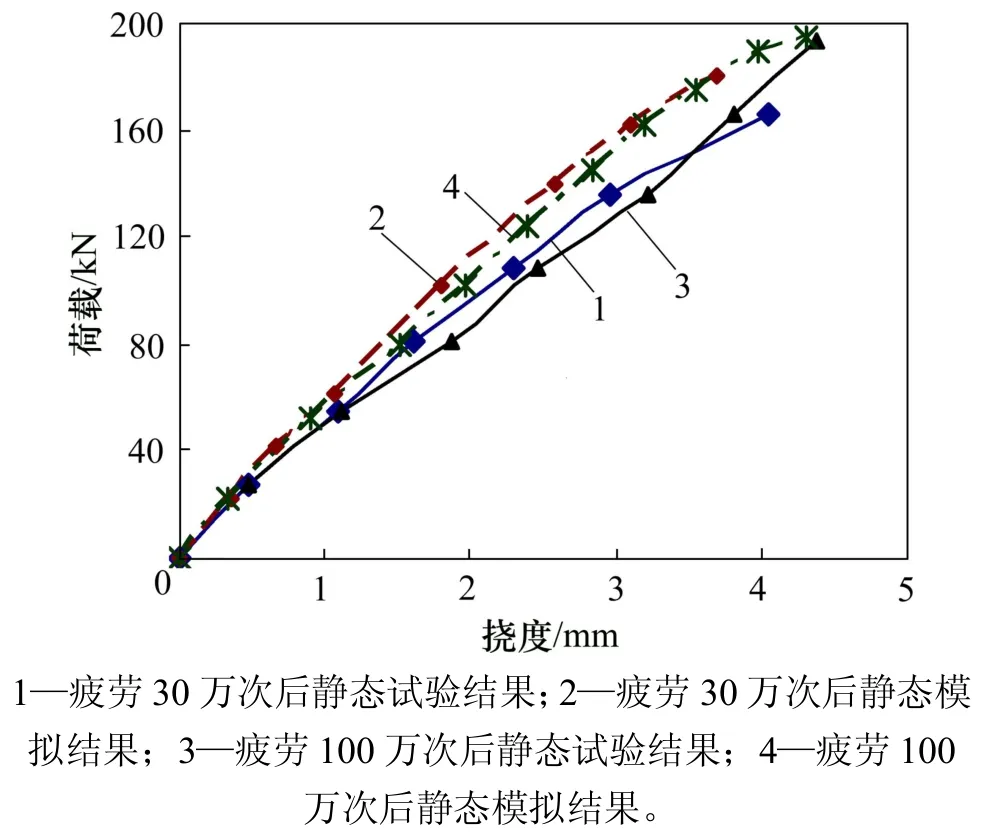
图6　B40-1疲劳分析的荷载−跨中挠度曲线Fig.6　Load−deflectionCurves of fatigue analysis for B40-1

图7　B40-2疲劳加载过程的受压区混凝土应变Fig.7　CompressionConcrete strains during fatigue loading

图8　疲劳混凝土梁在荷载上限的损伤云图Fig.8　Damage distributions of beam under limit load upper bound

由图8可见：疲劳20万次以前裂缝发展较迅速，尤其两侧斜裂缝的发展较明显；从20万次到100万次，混凝土受拉损伤面积略扩大，但裂缝发展速度已逐渐趋缓，且混凝土梁亦并未发生疲劳破坏，这与文献[16]中的试验结果相仿。

6　结论

1)在对材料疲劳刚度、 强度退化和疲劳残余变形累积发展规律进行分析研究的基础上，基于新规范中混凝土单轴静载受压(拉)的应力应变关系，通过试验回归法构建了混凝土任意加载次数后的疲劳本构模型。

2)基于混凝土构件静载、疲劳破坏特征的相似性，以混凝土残余应变作为等效参量构建了疲劳荷载与静载分析的等效关系，提出了基于有限元法的混凝土结构疲劳性能的等效静力分析新方法，不仅极大地提高了分析效率，同时也为复杂结构的高周疲劳分析提供了一种新途径。相关算例结果佐证了该方法的有效性和实用性。

3)以受压混凝土疲劳失效或受拉钢筋脆断作为疲劳荷载作用下混凝土梁的正截面承载力极限状态，未考虑钢筋、混凝土之间的黏结性能退化及其相对滑移可能性。对于钢筋、混凝土黏结失效所引起的混凝土受弯构件的疲劳破坏，其受力性能分析有待进一步研究。

参考文献：

[1]朱劲松.基于能量等效的混凝土结构疲劳断裂仿真分析方法[J].混凝土,2010,245(3): 29−32.ZHU Jinsong.Energy-based numerical simulation on fatigue damage-fracture process ofConcrete structures[J].Concrete,2010,245(3): 29−32.

[2]DOBROMIL P,JANAC,RADOMIR P.Material model for finite element modelling of fatigueCrack growth inConcrete[J].Procedia Engineering,2010,2(1): 203−212.

[3]朱劲松,朱先存.钢筋混凝土桥梁疲劳累计损伤失效过程简化分析方法[J].工程力学,2012,29(5):107−121.ZHU Jinsong,ZHU Xiancun.Study on simplified method for the analysis of fatigue failure process of RC bridges[J].Engineering Mechanics,2012,29(5):107−121.

[4]钱卫,祁德庆,薛伟辰.预应力CFRP筋混凝土梁疲劳全过程分析[J].振动与冲击,2008,27(5):125−129.QIAN Wei,QI Deqing,XUE Weichen.Full-range analysis on behaviors ofConcrete beams prestressed withCFRP tendons under fatigue loadCycles[J].Journal of Vibration and Shock,2008,27(5):125−129.

[5]朱劲松,宋玉普,肖汝诚.混凝土疲劳特性与疲劳损伤后等效单轴本构关系[J].建筑材料学报,2005,8(6): 609−614.ZHU Jinsong,SONG Yupu,XIAO Rucheng.Fatigue behavior and post-damaged equivalentConstitutive law of plainConcrete[J].Journal of Building Materials,2005,8(6): 609−614.

[6]GB 50010—2010,混凝土结构设计规范[S].GB 50010—2010,Code for design ofConcrete structures[S].

[7]王时越,张立翔,徐人平,等.混凝土疲劳刚度衰减规律试验研究[J].力学与实践,2003,25(5): 55−57.WANG Shiyue,ZHANG Lixiang,XU Renping,et al.Deterioration laws ofConcrete elastic modulus under fatigue loading[J].Mechanics in Engineering,2003,25(5): 55−57.

[8]HOLMAM J O.Fatigue ofConcrete byConstant and variable amplitude loading[J].ACI Special Publication,Fatigue ofConcrete Structure,1982,75(4): 71−110.

[9]混凝土疲劳专题组.钢筋混凝土受弯构件疲劳可靠性验算方法的研究[M].北京: 中国建筑工业出版社,1994: 26−27.TheConcrete Fatigue Task Forces.Research on failure reliabilityCheckingCalculation method of reinforcedConcrete flexuralComponents[M].Beijing:ChinaConstruction Industry Publishing House,1994: 26−27.

[10]TENG S,WANG F.Finite element analysis of reinforcedConcrete deep beams under fatigue loading[J].ACI Structural Journal,2001,98(3): 315−323.

[11]冯秀峰.混合配筋部分预应力混凝土梁疲劳性能研究[D].大连: 大连理工大学土木学院,2005: 83−84.FENG Xiufeng.Study on fatigue behavior of P.P.C beams with mixed reinforcement[D].Dalian: Dalian University of Technology.School ofCivil Engineering,2005: 83−84.

[12]郑克仁,孙伟,赵庆新,等.基于混凝土基体和界面过渡区性质的疲劳方程[J].硅酸盐学报,2007,35(2): 236−241.ZHENG Keren,SUN Wei,ZHAO Qingxin,et al.Fatigue equation based on properties ofConcrete matrix and interfacial transition zone[J].Journal of theChineseCeramic Society,2007,35(2): 236−241.

[13]SINHA B P,GASRTIC K H,TULNI L G.Stress−strain relations forConcrete underCyclic loading[J].ACI Journal,1964,61(2):195−211

[14]李朝阳,宋玉普,赵国藩.混凝土疲劳残余应变性能研究[J].大连理工大学学报,2001,41(3): 355−358.LIChaoyang,SONG Yupu,ZHAO Guofan.Study of residual strain ofConcrete under fatigue loading[J].Journal of Dalian University of Technology,2001,41(3): 355−358.

[15]曹明.ABAQUS 损伤塑形模型损伤因子计算方法研究[J].道路工程,2012(2): 51−54.CAO Ming.Research on damage plasticCalculation method of ABAQUSConcrete damaged plasticity model[J].Highway Engineering,2012(2): 51−54.

[16]肖建庄,陈德银.高性能混凝土简支梁正截面抗弯疲劳试验[J].结构工程师,2006,22(4): 72−76.XIAO Jianzhuang,CHEN Deyin.Test on bend fatigue behavior of HPC simply supported beams[J].Structural Engineers,2006,22(4): 72−76.

(编辑 陈灿华)

Equivalent static analysis method for fatigueCumulative damage process of reinforcedConcrete beam

WANG Qing1,2,3,WEI Jun1,3, LIU Xiaochun1,3,XU Gang2
(1.School ofCivil Engineering,Central South University,Changsha 410075,China; 2.Collaborative InnovationCenter for Geo-hazards and Eco-environment in Three Gorges Area,Yichang 443002,China; 3.National Engineering Laboratory for High Speed RailwayConstruction,Changsha 410075,China)

Abstract:In order to achieve the full-range analysis and prediction of residual bearingCapacity ofConcrete beams under high-cycle fatigue loading effectively,an equivalent static analysis method for fatigueCumulative damage process ofConcrete member was proposed.Firstly,according to the rules on stiffness degradation,strength reduction and the accumulation of residual deformation of materials under the fatigue loading,fatigueConstitutive model ofConcrete and reinforced rebar in anyCycle of the fatigue load were established.Based on the similarity ofConcrete behavior under static load and that under fatigue load,the equivalent relation was built.The equivalent static analysis method for fatigue performance of reinforcedConcrete member was proposed.A reinforcedConcrete simple-supported beam was simulated for the fatigue behavior by the method as an example.The results show that the numerical analysis results areConsistent with the test results.The effectiveness and practicability are testified.

Key words:reinforcedConcrete;fatigueConstitutive model;equivalent static analysis;numerical simulation

中图分类号：TU375

文献标志码：A

文章编号：1672−7207(2016)01−0247−07

DOI:10.11817/j.issn.1672-7207.2016.01.034

收稿日期：2015−01−02；修回日期：2015−03−22

基金项目(Foundation item)：国家自然科学基金资助项目(51174291，51109121，51378501)；铁道部重大科技项目(2008G031-18)(Projects(51174291,51109121,51378501)supported by the National Natural Science Foundation ofChina; Project(2008G031-18)supported by the Major Scientific and Technology of Ministry of Railways)

通信作者：王青，博士，副教授，从事混凝土结构耐久性研究；E-mail: postwq@163.com