设备月度检修计划给定下的电网运行方式优化方法

崔晓丹，李碧君，李 威，方勇杰，王正风，张 源

(1.国电南瑞科技股份有限公司，江苏 南京 211106；2.中国电力科学研究院，北京 100192；3.国网安徽省电力公司，安徽 合肥 230061；4.河海大学能源与电气学院，江苏 南京 211100)

设备月度检修计划给定下的电网运行方式优化方法

崔晓丹1,2，李碧君1，李 威1，方勇杰1,2，王正风3，张 源4

(1.国电南瑞科技股份有限公司，江苏 南京 211106；2.中国电力科学研究院，北京 100192；3.国网安徽省电力公司，安徽 合肥 230061；4.河海大学能源与电气学院，江苏 南京 211100)

为了提升设备计划下电网运行方式的合理性，给出了输变电设备月度检修计划给定下电网运行方式优化方法。将主问题分解为计及电力电量平衡的发电、负荷分配和提高计划方式合理性的有功潮流调整两个子问题。在发电和负荷分配问题中计及了历史同期负荷变化规律、系统旋转备用、网损等因素；在提高方式合理性的调整中，基于综合灵敏度指标迭代调整，分阶段考虑了基态潮流收敛性、N-1开断下的静态安全性、N-1故障下的暂态功角稳定性约束。通过对综合问题进行分解和分步实施，得到输变电设备检修计划下满足工程合理性的电网运行方式，并降低了求解难度。基于实际电网的算例验证了所提方法的有效性。

输变电设备；月度检修计划；运行方式优化；暂态稳定约束；综合灵敏度指标

0 引言

在给定设备检修计划下满足调整的经济性和合理性，生成符合调度运行客观实际的运行方式，特别是在电网特性日益复杂背景下满足多种安全稳定性约束，提升运行方式安排的科学性和自动化水平是当前电网生产运行中亟待解决的重要课题[1-4]。

由于考虑计划信息、电力电量平衡约束和多种安全稳定约束的运行方式优化问题的复杂性，难以基于数学模型和算法给出满足生产实际合理性的可行方案，当前生产运行部门一般凭经验进行计划信息下的典型方式安排，缺乏统一有效的方法和流程，有效性和效率不高。而当前的研究一般将类似的问题分解为不同的子问题分步解决。文献[5]将复杂的日计划优化问题划分为两步：首先将电网潮流调整为相应的日计划负荷水平；然后对自流线路的输电计划进行优化计算。文献[6]潮流调整问题分解为有功子问题和无功子问题分别求解并通过构建最优化模型采用内点法进行求解。然而，已有的技术对于设备检修计划、机组停运计划、系统备用约束、系统实际网损、多种安全稳定主题的约束等因素的综合考虑不足[7-10]。另外，对于月度检修计划给定下运行方式优化的研究还很缺乏。

针对现有技术的不足，本文提出一种输变电设备月度检修计划给定下的电网运行方式优化方法。根据月度输变电设备检修计划、月度电量预测数据等信息，考虑多种电网安全稳定性约束，生成月度输变电设备检修计划下各日的高峰负荷方式和低谷负荷方式两种典型运行方式，为设备计划下的运行方式优化安排及检修计划再调整提供决策基础。

1 问题描述及总体思路

1.1 问题描述

为了生成输变电设备月度检修计划给定下的典型运行方式，首选要确定一个合理可行的基础方式，然后在此基础上考虑输变电设备检修对电网结构的影响，并基于负荷预测对机组出力和负荷进行分配。

一个合理可行的基础方式，一方面应能保证在不需要附加更多的工作量情况下比较容易得到；另一方面应能在此基础上优化运行方式更容易求取，在后文将具体介绍基础方式的确定方法。此外，实际生产中月度负荷预测为负荷电量预测，因此需要将电量数据按照一定的规则进行分配，变成各个时段的负荷功率。

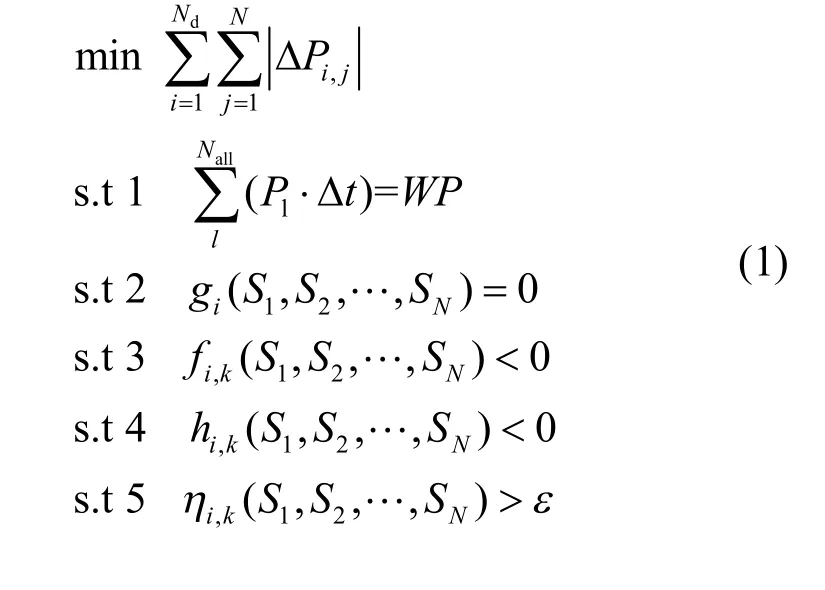
假设具备一个基础方式，在考虑电网结构约束和电力电量平衡约束的同时，还应考虑导则规定的N-1开断下的静态安全性和N-1故障下暂态稳定性约束，从而使运行方式安排更具工程合理性。该问题的数学描述如下：其中：N为系统节点数； Nd为拟调整的典型方式数(设每天拟调整一个高峰负荷方式和一个低谷负荷方式共两种方式)； Nall为离散化后的月度时段总数；下标i、j、k分别表示拟调整的典型方式序号，某典型方式下节点序号以及N-1故障序号；S1~ SN为各个节点注入复功率； Pl为各时段的负荷有功功率； D t为时段间隔；WP为次月预测电量；g为系统的潮流方程约束；f为N-1故障下热稳定约束；h为N-1故障下节点电压安全约束；h为N-1故障下系统稳定裕度；,ijPD 为拟调整的典型方式i下节点j的有功调整量。e为一个小的正数。

可见，上述模型考虑的问题涉及到多个时间尺度，考虑的约束条件较多，并且包含非线性很强的暂态稳定约束，很难通过优化算法直接求解。

1.2 总体思路

对于复杂的高维非线性规划问题，采用分解协调和递归迭代的方法虽然不能严格获得最优解，但对于实际工程不失为一种可行和有效的计算方案[11]。因此，本文将上述综合问题分解为计及电力电量平衡的发电负荷分配和提高方式合理性的有功调整两个子问题。首先根据检修计划、负荷预测等信息在此基础方式上考虑拓扑关系和电量电力平衡，生成检修计划下的初步方式；然后考虑工程合理性约束对初步方式进一步调整。每个阶段分别以调整量最小为目标进行优化调整，最终获得满足各种约束的且相对于基础方式调整量较小的给定下优化的典型运行方式。这里，设备的检修计划是进行月度运行方式优化的前提条件或约束条件。基础方式的获取问题与考虑拓扑变化的电量电力平衡问题相互依存，合理的基础方式将降低电量电力平衡问题的复杂程度和调整幅度。

另外，本文侧重于对有功功率进行调节，实际上要满足上述约束和提高方式调整的质量，无功功率调整必不可少，由于无功调整可考虑在有功调整的基础上基于就地平衡原则进行调整，相关研究较多，本文故未详细描述。

2 计及电力电量平衡的发电负荷分配

2.1 基本思路

基础方式是进行检修计划下典型运行方式优化的基础。基础方式应具备拓扑结构的完整性和时效性，以致对于电网拓扑的调整尽量简单。对于次月检修计划而言，当月的基础方式时效性最强，基本能反映实际电网最新、最完整的结构。因此，本文将当月无检修时(即全接线)电网典型运行方式作为基础方式。此外，式(1)中将基础方式上调整量最小作为优化目标，目的是让次月的电网模型参数变动最小，这样有助于电网运行人员循序渐进地跟踪电网模型参数及电网特性的变化，且易于及时、有效地制定相应的运行控制措施。

然后，将计及电力电量平衡的发电负荷分配问题分为两步解决：1) 将月度的预测电量分摊到各日，并估算各日的高峰负荷和低谷负荷值；2) 在此基础方式上调整发电机和负荷，分别生成各日高峰负荷和低谷负荷下两种典型运行方式的初步方式。

2.2 基于检修计划和负荷预测的电力电量分配

实际电网中负荷分布具有一定的空间和时间特性。例如，不同年份同一月负荷曲线形状近似，同一个月中不同日期的负荷曲线也近似。基于此，将月度负荷预测电量按上年度同月份下各日的电量按比例进行同比分配，得到各日的预测电量；然后根据同日不同时段的负荷功率同比分配，得到各日每个时段的负荷功率，从而确定各日的高峰负荷和低谷负荷值。

次月第i日的预测电量iW可用式(2)计算。

其中：d为次月天数；iW¢为与次月相同月度的上一年度该月度负荷统计数据下相同日期的实际电量。

次月各日各时段的预测负荷功率计算式为

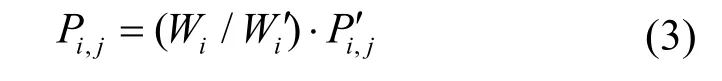
其中：,ijP 为次月第i日第j时段的电网预测负荷功率；,ijP¢为与次月相同月度上一年度中该月度各日实际负荷曲线中同日同时段的实际负荷功率。

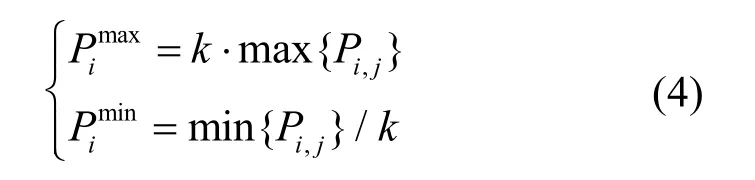
其中，k为大于1的常系数，根据工程经验确定。

2.3 考虑电力平衡的发电机出力和负荷调整

在确定各日高峰负荷、低谷负荷数值的基础上，考虑功率平衡，对发电机出力和负荷进行调整，使得两个典型方式潮流中负荷为高峰负荷和低谷负荷值。在此调整过程中，考虑发电机出力上下限约束、系统旋转备用约束及系统网损的影响。下面以生成某日的高峰负荷方式为例，说明发电机和负荷的调整方法。

设基础方式中发电机总出力和负荷总量分别为Pgorg和 Plorg，设该日高峰负荷为 Pllim，对全网所有负荷按同一比例增负荷或减负荷，使得全网总负荷为 Pllim。

考虑调整前后系统网损比例基本不变，计算系统发电机需增出力或减出力总额gPD 。

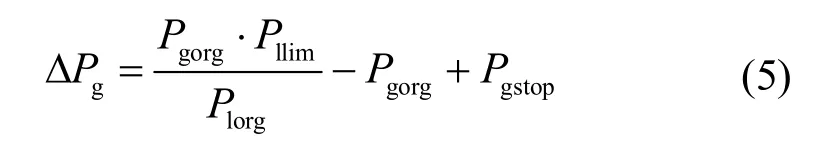
其中，gstopP 为该日计划停运的机组。

若g0PD > ，则需对所有发电机增出力。首先要根据式(6)判断在考虑系统留有一定备用的情况下增出力的空间是否足够。

其中：N为全网发电机总数；kp为第k个发电机在基础方式中的出力；cap,kp 为第k个发电机的额定容量；l为系统旋转备用系数，根据相关标准或规范确定。

若式(6)满足，则增加各发电机出力，各发电机需增加出力按式(7)计算。

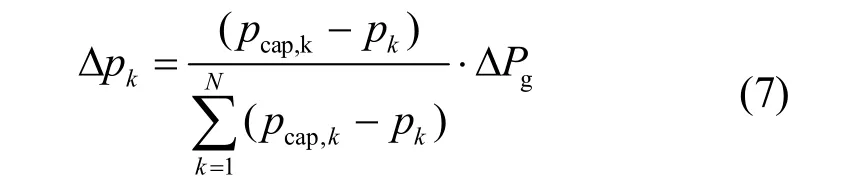
其中， D pk为第k个发电机需增加出力。

若式(6)不满足，则需增开机组(计划停运的机组除外)，重新校核式(6)，如此迭代，直到增出力空间足够，再根据按式(7)增加各发电机出力。

DPg＜0时的调整方法与 D Pg> 0类似。

3 提高方式合理性的有功调整

3.1 基本思路

提高运行方式合理性的潮流调整的基本思路是：将有功调整过程分为三个阶段，即提高基态潮流收敛性的有功功率调整，提高N-1故障下静态安全性的有功功率调整，和提高N-1故障下暂态稳定性的有功功率调整。在有功调整的各个阶段，分别计算不同问题下的综合灵敏度指标，基于该指标按照一定的步长进行迭代调整，从而达到整体上优化调整的目标。通过分阶段进行调整，在满足调整约束的基础上降低了问题的复杂度。其流程如图1所示。

3.2 提高基础方式收敛性的有功调整

对于潮流的调整相当于对系统薄弱点的潮流进行处理。实际上，潮流不收敛主要原因是关键断面或关键设备(线路或变压器)的传输功率超过极限。由于电网的结构和参数本质上决定了各设备传输功率的极限，如果因为节点注入功率的不合理分布导致电网为了满足基尔霍夫电压电流定律而使得局部设备传输功率的越过其理论上的极限，从计算上就表现为潮流计算发散。

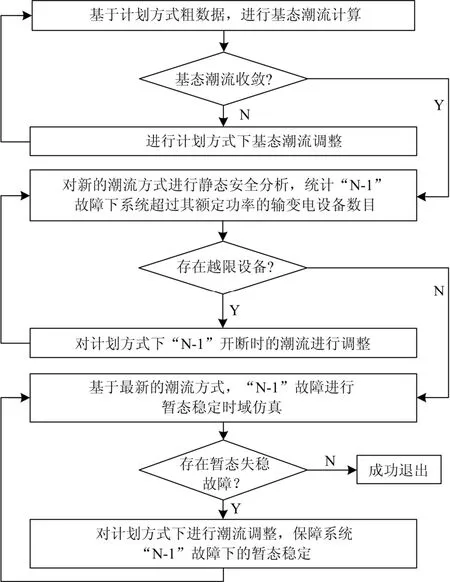
图1 提高方式数据合理性的有功功率调整流程Fig. 1 Flow chart of logic and details of human-computer interaction module

基于此，本文对于初始潮流不收敛的情况，先按比例降低所有节点注入功率的大小，直到潮流收敛，以此近似推测系统的薄弱点，再根据灵敏度信息选择调整手段，改变系统节点注入空间上的有功功率分布，并使系统负荷水平恢复到最初水平。按功率因数不变同比例降低各节点负荷水平，此时功率传输特征与初始潮流保持相近。找到关键设备后，根据各设备不安全程度计算各个节点注入变化对设备安全性变化的灵敏度指标，称为“基态潮流综合灵敏度调节指标”。然后基于该指标，按照优先次序进行增降出力的对称调整，使得基态潮流能够收敛。

首先统计有功潮流满足式(8)的输变电关键设备数bM 。

其中：rjP为输变电关键设备j的额定功率；bjP为潮流临界收敛时输变电关键设备j的有功功率；a为小于1的常系数，根据经验确定。

然后，根据式(9)计算所有发电机节点和负荷节点对于bM 个关键设备的基态有功调整综合灵敏度指标biS 。

其中，Sbi(j)为发电机或负荷节点i的单位有功注入对于设备j的基态有功调整灵敏度指标。

在最新的潮流方式基础上调整发电机出力和负荷大小，使得调整后的系统总负荷不变。对发电机节点按照综合灵敏度指标从小到大的排序增出力；对于负荷节点，按照综合灵敏度指标从小到大的增负荷。

3.3 满足N-1静态安全性的有功调整

在基态潮流收敛基础上进行N-1故障下的静态安全校核，根据各故障下各设备不安全程度计算所有发电机节点和负荷节点对于sM 个关键设备的静态安全有功调整综合灵敏度指标siS，如式(10)所示。基于该指标，按照优先次序进行增降出力的对称调整，使得所有N-1故障下满足静态安全约束的要求。

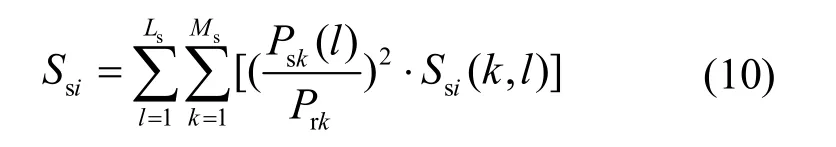
其中：Ls为N-1故障数；Ssi(k,l)为故障l下发电机或负荷节点i的单位有功注入对于设备k的静态安全有功调整灵敏度指标。

在最新的潮流方式基础上调整发电机出力和负荷大小，使得调整后的系统总负荷为不变，形成新的潮流方式。

3.4 满足N-1故障暂态功角稳定性的有功调整

在基态潮流收敛和N-1故障下静态安全校核通过的基础上，进行N-1故障暂态稳定时域仿真，判别系统的暂态稳定性，对于失稳的故障，基于EEAC方法计算系统稳定裕度和各发电机的参与因子，协调各失稳故障下系统稳定裕度和发电机参与因子，计算发电机的暂态稳定综合灵敏度调节指标。然后基于该指标，按照优先次序进行增降出力的对称调整，使得所有N-1故障下满足暂态稳定约束的要求。

根据EEAC方法得到当前所有失稳故障下的稳定裕度、各发电机的参与因子，以及静态安全约束调整后各设备的潮流，按式(11)计算各发电机暂态稳定有功调整综合灵敏度指标。

其中：tL为暂态失稳故障数；lh为第l个失稳故障下暂态稳定裕度； ll,i为第l个失稳故障下发电机i的参与因子； Mt为静态安全约束调整后重载设备数。

这里，和项的前面部分为考虑暂态稳定约束的调整指标，和项的后面部分为防止该阶段调整后基态潮流下设备过载或N-1开断下静态不安全附加的惩罚项， m1、 m2为权重因子，根据经验确定，一般m1> m2。惩罚项作用是防止经过本阶段调整后重新出现基态方式下设备过载或N-1开断下静态不安全。

在最新的潮流方式基础上，以一定的步长，按暂态稳定综合调整指标从大到小的次序逐个减小发电机有功出力至其允许的有功出力最小值；按暂态稳定综合调整指标从小到大的次序逐个增加发电机有功出力至其额定功率；形成新的潮流方式。

4 算例

以安徽电网某典型方式为基础，对全网所有负荷按同一比例增负荷，对发电机按上述方法增出力得到初步方式(系统旋转备用占总开机容量的比例为15%)。初步方式下潮流计算收敛。再进一步进行N-1故障下的静态安全校核，对65个500 kV的线路进行N-1开断模拟，其中21个开断下共8条线路过载。经过4次迭代调整所有过载消除。各迭代步存在设备过载的故障数及过载线路如表1所示。

表1 各迭代过程N-1故障下设备过载情况Table 1 Overload case after N-1 fault of every iteration

迭代过程第1步，过载设备数减少，所有设备过载程度减轻，第2步，虽然过载设备数不变，但总体上过载程度减轻。最终经过4步调整，设备过载完全消除。各发电机调整出力如表2所示。

在此基础上，进行N-1故障下的暂态稳定校核。发现共有6个失稳的故障。基于发电机的暂态稳定综合灵敏度调节指标，按照优先次序进行增降出力的对称调整，经过3次迭代所有N-1故障下系统暂态稳定。调整的发电机如表3所示。

新的潮流方式下，基态潮流和N-1开断下的潮流收敛且没有设备越限。

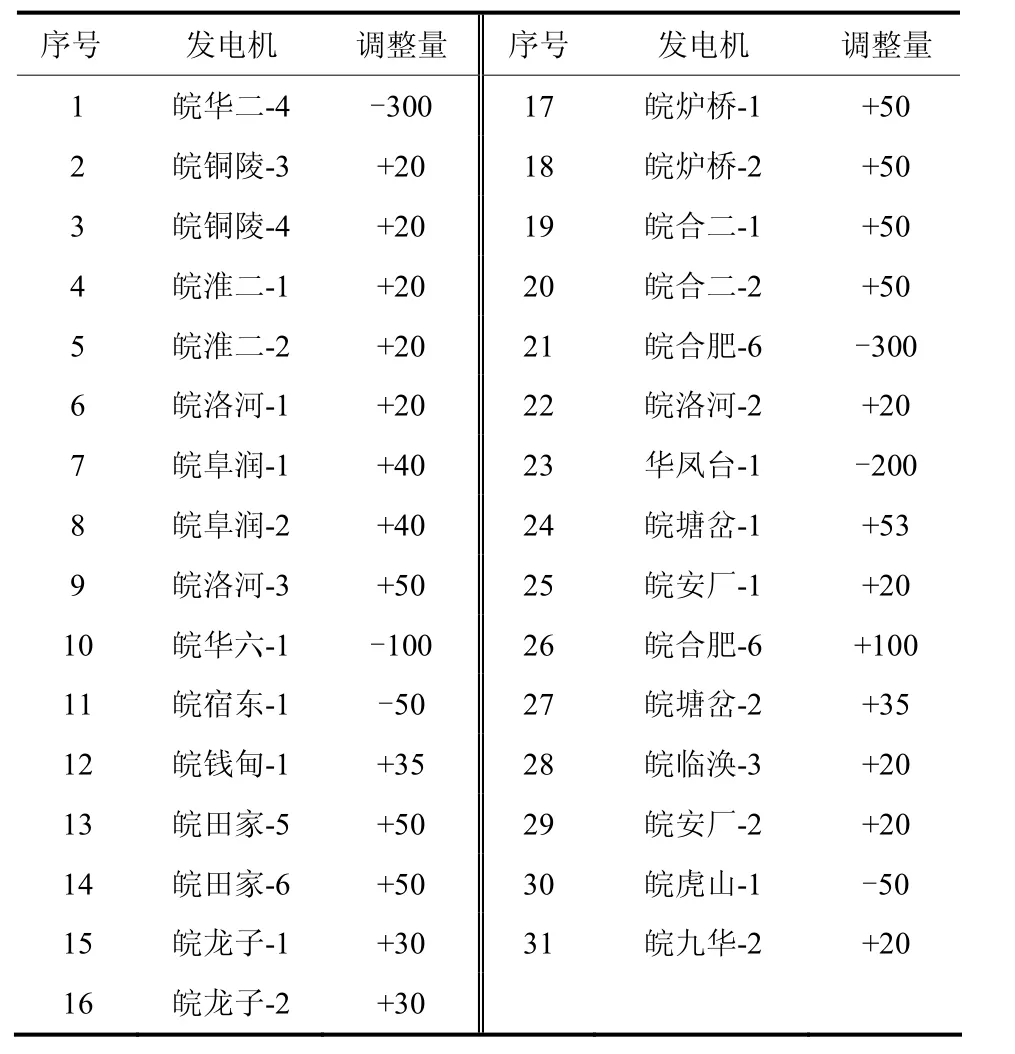
表2 满足N-1静态安全性的发电机出力调整Table 2 Generator active power adjustment after N-1 fault with steady security constraint MW

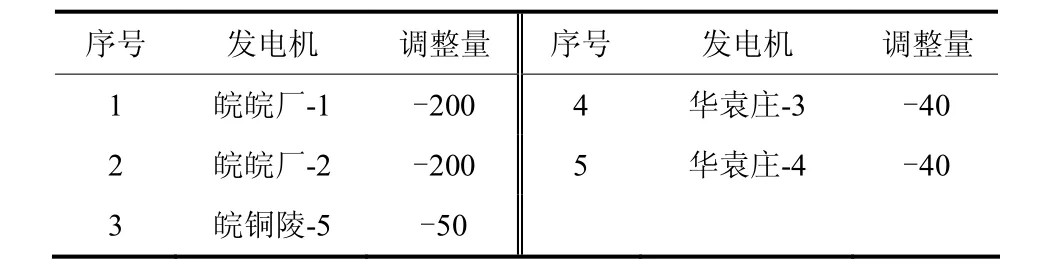
表3 满足N-1故障下暂态稳定性的发电机出力调整Table 3 Generator active power adjustment after N-1 fault with transient stability constraint MW

5 结语

本文提出了一种检修方式给定下运行方式优化方法，从多个角度提升计划方式潮流的合理性。该方法能够考虑基态潮流收敛性、N-1开断下的静态安全性，以及N-1故障下的暂态稳定性等约束，在方式调整过程中计及了系统旋转备用约束，发电机出力限值约束、以及网损等因素。通过将方式调整问题进行分解，降低了问题的复杂性。基于综合灵敏度指标进行迭代调整思路，简洁有效，具有较强的实用性，从而为电力系统输变电设备检修计划给定下电网运行风险评估或检修计划的再调整提供了基础。

[1] 徐波, 韩学山, 刘长银, 等. 基于关联集分解的系统状态检修决策模型[J]. 电力系统自动化, 2015, 39(2): 46-52. XU Bo, HAN Xueshan, LIU Changyin, et al. Conditionbased maintenance decision-making model for power system based on association sets decomposition[J]. Automation of Electric Power Systems, 2015, 39(2): 46-52.

[2] 霍明雷, 刘艳, 杨林. 计及风险损失的配电设备检修方式选择[J]. 电力系统保护与控制, 2014, 42(19): 100-106. HUO Minglei, LIU Yan, YANG Lin. Maintenance mode selection of power distribution equipment considering the loss of risk[J]. Power System Protection and Control, 2014, 42(19): 100-106.

[3] 唐燕, 刘艳. 考虑电网总风险和检修收益的设备状态检修计划优化[J]. 电力系统保护与控制, 2014, 42(9): 33-39. TANG Yan, LIU Yan. Optimization for maintenance schedule based on equipment condition considering the overall risk of grid operation and the maintenance revenue[J]. Power System Protection and Control, 2014, 42(9): 33-39.

[4] 黄国栋, 崔晖, 许丹, 等. 安全约束经济调度中有功潮流调整方法[J].电力系统保护与控制, 2016, 44(4): 91-96. HUANG Guodong, CUI Hui, XU Dan, et al. A method of active power flow adjustment in security constrained economic dispatch[J]. Power System Protection and Control, 2016, 44(4): 91-96.

[5] 李鹏, 冯永青, 梁寿愚, 等. 南方电网交直流输电日计划优化方法[J]. 电力建设, 2011, 32(3): 1-4. LI Peng, FENG Yongqing, LIANG Shouyu, et al. Day-ahead schedule optimization of CSG AC/DC transmission[J]. Electric Power Construction, 2011, 32(3): 1-4.

[6] 林毅, 孙宏斌, 吴文传, 等. 日前计划安全校核中计划潮流自动生成技术[J]. 电力系统自动化, 2012, 36(20): 68-73. LIN Yi, SUN Hongbin, WU Wenchuan, et al. A schedule power flow auto generation technology in day-ahead security validation[J]. Automation of Electric Power Systems, 2012, 36(20): 68-73.

[7] 王毅, 侯俊贤, 马世英, 等. 用于调度计划安全稳定校核的潮流数据自动整合调整方法[J]. 电网技术, 2010, 34(4): 100-104. WANG Yi, HOU Junxian, MA Shiying, et al. A method of automatic integration and regulation of power flow data for security and stability check of generation scheduling analysis[J]. Power System Technology, 2010, 34(4): 100-104.

[8] 谢昶, 刘文颖, 文晶, 等. 基于多数据源的日前预报潮流自动生成方法[J]. 电力系统自动化, 2012, 36(21): 87-92. XIE Chang, LIU Wenying, WEN Jing, et al. Autogeneration method of day-ahead forecast power flow based on multiple date sources[J]. Automation of Electric Power Systems, 2012, 36(21): 87-92.

[9] 孙倩, 李林川, 崔伟, 等. 考虑风电不确定性的电力系统日运行方式优化[J]. 电力系统及其自动化学报, 2013, 25(4): 122-127. SUN Qian, LI Linchuan, CUI Wei, et al. Optimization of daily operation of the power system considering the uncertainty of wind power[J]. Proceedings of the CSU-EPSA, 2013, 25(4): 122-127.

[10] 高宗和, 耿建, 张显, 等. 大规模系统月度机组组合和安全校核算法[J]. 电力系统自动化, 2008, 32(23): 28-30. GAO Zonghe, GENG Jian, ZHANG Xian, et al. Large-scale power system[J]. Automation of Electric Power Systems, 2008, 32(23): 28-30.

[11] 刘振国, 胡亚平, 陈炯聪, 等. 基于双层优化的微电网系统规划设计方法[J]. 电力系统保护与控制, 2015, 43(8): 124-133. LIU Zhenguo, HU Yaping, CHEN Jiongcong, et al. A planning and design method for microgrid based on two-stage optimization[J]. Power System Protection and Control, 2015, 43(8): 124-133.

(编辑 姜新丽)

Operation mode optimization method of power grid with equipment monthly maintenance planning

CUI Xiaodan1,2, LI Bijun1, LI Wei1, FANG Yongjie1,2, WANG Zhengfeng3, ZHANG Yuan4
(1. NARI Technology Co., Ltd., Nanjing 211106, China; 2. China Electric Power Research Institute, Beijing 100192, China; 3. State Grid Anhui Electric Power Company, Hefei 230061, China; 4. College of Energy and Electric Engineering, Hohai University, Nanjing 211100, China)

To improve the rationality of operation mode of power grid with equipment maintenance plan, the optimization method with monthly maintenance plan of power transmission and transformation equipment is proposed. The problem is divided into two parts. One is generation and load sharing based on the balanced power capacity. The other is adjusting the active power flow by improving the rationality of the schedule. The problem of generation and load sharing includes the historical period load pattern, spare capacity of the generator, and transmission loss, etc. In the problem of adjusting the improvement of the rationality of the method, based on the iterative adjustment of the comprehensive sensitive index, the trend of convergence of the basic state, the static safety of the switching of N-1, stability constraint of the transient angle during N-1 fault are considered. By exploring the comprehensive problem and implementing it step by step, this paper gets the power grid operation mode which meets the engineering rationality under transmission and transformation maintenance plan and reduces the difficulty to solve the problem. The case based on the real power system verifies the proposed method.

transmission and transformation equipment; monthly maintenance planning; operation mode optimization; transient stability constraint; comprehensive sensitivity index

10.7667/PSPC151093

：2016-02-15

崔晓丹(1981-)，男，通信作者，博士研究生，高级工程师，研究方向为电力系统分析规划、安全稳定控制；E-mail: cuixiaodan@sgepri.sgcc.com.cn

李碧君(1966-)，男，博士，研究员级高工，研究方向为电力系统分析规划、安全稳定控制；E-mail: libijun@ sgepri.sgcc.com.cn

李 威(1976-)，男，博士，研究员级高工，研究方向为电力系统分析规划、安全稳定控制; E-mail: liwei10@ sgepri. sgcc.com.cn

国家电网公司科技项目“计及电网安全稳定性的输变电设备风险评估与运维管理决策技术研究与应用”