基于分段插值同步化算法的谐波测量

吴超凡，陈隆道

(浙江大学电气学院，浙江 杭州 310027)

基于分段插值同步化算法的谐波测量

吴超凡，陈隆道

(浙江大学电气学院，浙江 杭州 310027)

传统的基于FFT的电力谐波测量方法由于频谱泄漏问题，在测量基频偏移信号或者频率不断波动的非稳态周期信号时存在着较大的误差。现采用一种时域插值的方法对非同步采样序列进行重新定位，依据序列的二次差商大小对信号进行分段并分别采用线性插值和Hermite插值两种算法进行二次同步化。在基频偏移固定和基频不断波动的两种情况下进行仿真计算。结果表明，分段插值同步算法能够适用于上述两种情况的谐波测量，在兼顾计算效率的同时，满足了GBT 17626.7-2008国标规定的精度要求，是一种具有实用性的方法。

非同步取样；同步化算法；分段插值算法；时变信号；频谱泄漏

0 引言

FFT算法因为能快速地分析谐波参数而在电力系统的数字信号处理技术中被广泛使用，能够满足工程上实时测量的要求。但是当信号频率发生偏移，甚至是基波频率不断变化的非稳态周期信号的特殊情况下，均匀采样频率和信号周期之间不再存在整数倍关系时，所截取的数据长度也不再是严格的整数倍信号周期。此时若直接对采样序列用FFT算法来分析谐波将会发生比较严重的频谱泄漏现象，频谱和其他相关电参量的测量结果也随之存在很大的误差。

为了减少因非同步取样而导致的频谱泄漏，可以对采样序列进行加窗处理并在FFT变换后的频谱系数插值来提高精度。通过加窗处理，一方面在时域上使得采样数据的边缘幅值趋于零，减小了非同步采样造成的不连续；而在频域上，采用的窗函数较矩形窗有更好的旁瓣表现，较低的旁瓣有效抑制了频谱泄漏造成的影响，文献[1-3]中采取了加窗函数并配合频域插值的方法来进行谐波分析。在对采样序列加窗减小了长范围的频谱泄漏后，还可以通过进一步的插值运算来消除短范围频谱泄漏[4-5]，但是这种方法较为复杂，计算量较大，而且其精度受到窗函数和采样长度的影响。例如基于Hanning窗和Black-Harris窗的插值算法都需要4个基波周期以上的数据，当要求的精度进一步增加，要求的采样数据也随之变多[6]。

也可以利用数字锁相环电路或者通过双速率采样等软件方法[7]来实现同步采样，进而避免频谱泄漏产生的误差。此类方法可以直接采用FFT变换，实时性好，但是不可避免地提高了硬件复杂度。

还有一种准同步采样法[8]，通过不断进行准同步迭代计算来消除同步误差的影响，该方法对采样电路的要求较低，但是由于需要多次的迭代计算，其算法较为复杂，实时性差。

此外，对非同步的采样序列采用时域插值或自适应计算[9]来进行二次同步化也不失为一种可行的方法。文献[10]提出了一种时域数据修正的同步化算法，通过对采样序列的插值使得处理后的序列尽可能接近理想的同步采样序列，然后再通过FFT进行相应的计算和分析。这种方法公式简单，允许非同步采样,仅需要保证采样数据中至少包含一个完整的周期即可,适用于实时性要求较高的场合。比如当电力系统发生振荡[11]或异步运行时，负荷点的频率也在相应地振荡，此时只有单周期的测量结果才有实际意义。又比如文献[12]和文献[13]中的光伏并网系统中由于非线性电力设备的使用存在着一定的谐波，出于对设备的控制和保护，具有高实时性的在线快速检测装置是很有意义的。在上述情况下，同步电路无法进入锁定状态；准同步采样和加窗插值法都需要对稳定频率的信号进行多个周期的采样，不适用于非稳态周期信号的谐波测量。而该时域插值重定位采样序列的方法可以适用于该高实时性的情况。

本文将在其基础上采用线性和Hermite分段插值的方法对非同步采样序列进行同步化处理，并用变频率信号进行仿真计算以验证其可行性。

1 非同步数据的重定位

对于非同步数据的同步化，首要的工作应该是确定信号的周期[14]。因为周期信号的数字化处理存在一定的延迟以及电网实际频率的偏移所产生的非同步，文献[15]对于不含直流分量的周期信号采取信号过零检测的方法来确定其周期，一般情况下，信号周期的计算分为中间部分的若干个完整采样周期和首尾的小数部分，即

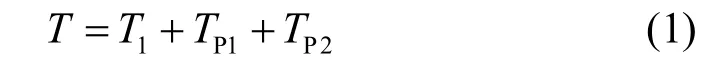
其中： T1代表一个信号周期中间的整数个采样周期部分，可以依据两个相同特征的过零点之间的采样点数来计算得到； TP1和 TP2分别代表信号始端和尾端的周期小数部分，可以通过对过零点附近的采样点进行插值来逼近信号在采样点附近的函数值，然后通过解函数方程来计算得到该小数部分。一个含有最高谐波次数为30次的周期信号，在过零点附近用一阶线性方程插值计算其周期，误差在0.009%以内[16]，足以满足一般工程上的精度需求。

设 x1(k)是包含一个完整信号周期的非同步采样序列，在计算出信号周期T之后，便可以由T得到理想的同步采样周期Tsi，为了后续FFT的方便，一般将T除以2的幂次方。因此，理想同步序列 x2(i)中的第i个同步采样点在实际采样序列中的下标为

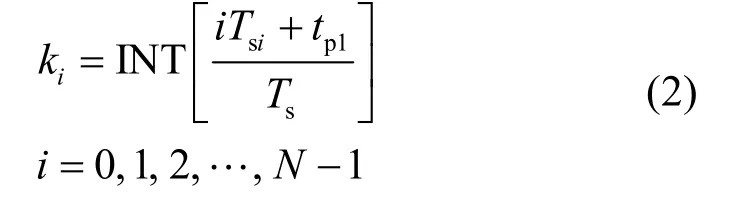
其中：INT[]为取整算子；Tsi为理想同步采样周期；Ts为实际采样周期；tp1代表实际采样序列和同步采样序列始端的时间差。在计算得到下标 ki后，就能够根据 ki和 ki+ 1点的实际采样值来构造插值函数得到同步化处理后的理想序列。

2 分段插值同步化算法

本文提出一种基于线性插值算法和Hermite插值算法的分段插值同步化算法，因为实际电网中的信号波形大致上近似于三角函数，其二阶导数大致上也和三角函数一样呈周期变化。在信号的过零点附近往往其斜率变化率不大，用线性插值便有足够高的精确度；而在信号的波峰和波谷附近，信号的二阶导数在一般情况下也到达极值，在图像上看，这段信号也拥有较大的曲率，此时若用线性插值算法则不大妥当，本文考虑采取Hermite插值算法来对这一段信号进行拟合。

在实际计算中，可以对得到的采样序列 x1(k)求取二次差商，再根据同步化序列 x2(i)中第i个点所对应的下标 ki处的二次差商大小来决定该点采用何种插值方式。

2.1 线性插值算法

根据式(2)，在完成了对采样序列的重新定位之后，若采用线性插值算法，可得

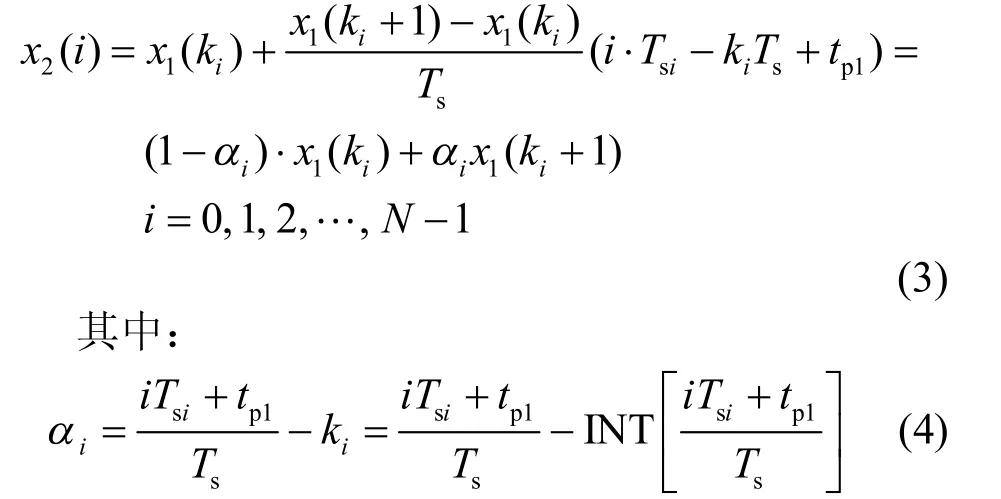
ai在计算下标 ki时就可得到，因此采取线性插值算法对斜率变化率较小处的点进行计算是非常简捷的。再对线性插值算法的误差进行分析，设同步化的取样点 ti处于实际采样序列的点 tki和点 tki+1之间，则在it点上有理论截断误差为

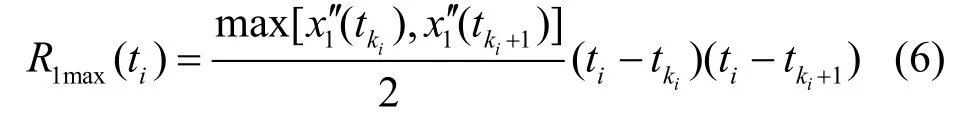
分析式(6)可知，当点 tki处的二次差商较小时，也意味着较小，线性插值截断误差 R1max(ti)在一个较小的范围内，在这种情况下采用线性插值可以在尽量不影响精度的前提下有效提高运算效率。

2.2 Hermite插值算法

已知两节点三次Hermite插值公式如下：

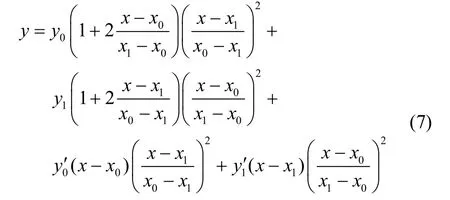
在计算得到ki后，由 ki和 ki+1点的函数值和一阶导数值代入式(7)并化简后可得构造两点的Hermite插值函数如下：

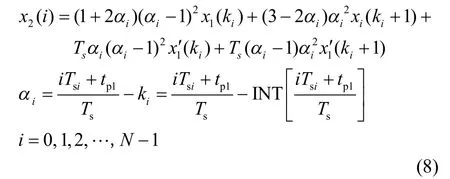
其中， x1¢()代表 x1()的一阶导数，可以用插值点前后的采样值差商运算近似求得：

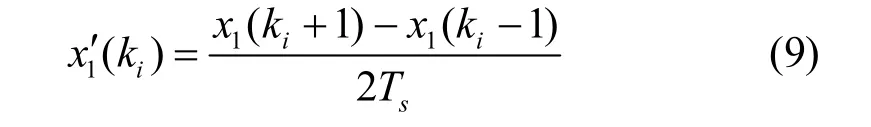
x¢(ki+ 1)同理，将式(9)代入式(8)就是对于采样序列的Hermite插值同步化公式。再对该算法的误差进行分析，设同步化的取样点ti处于实际采样序列的点

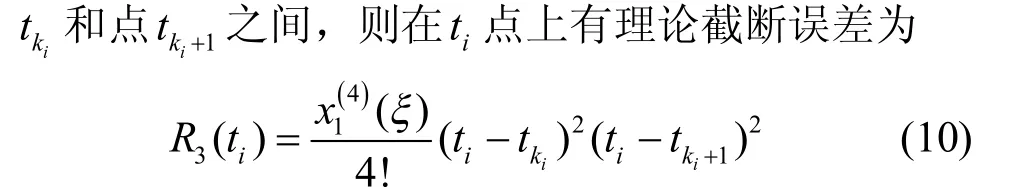
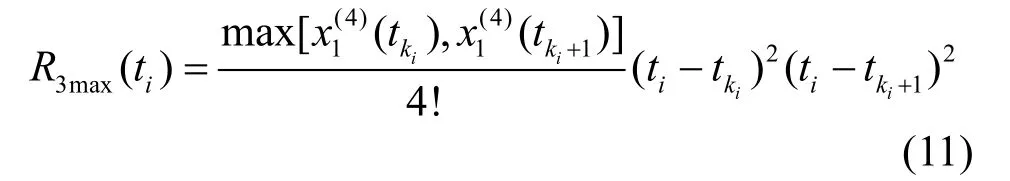
值得一提的是，抛物线插值算法的截断误差为

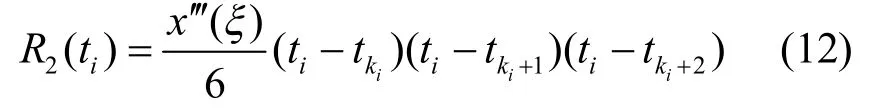
通过对比式(10)和式(12)不难发现，Hermite插值的截断误差比抛物线插值的误差拥有更高的阶数，所以 R3较之 R2要更小，即在采样序列波形的斜率变化率较大的地方采用Hermite插值可以提高插值的精度。

3 仿真计算和分析

3.1 固定频率信号仿真分析

考虑到电网中的实际信号的谐波成分中以奇次谐波为主，同时出于方便观察的目的对谐波幅值进行设定，有一信号如下：

其中，f是电网的基波的实际频率，取f为49.5 Hz，49.7 Hz，50 Hz，50.3 Hz，50.5 Hz作为频率测试点。在仿真计算时，取采样频率为6 400 Hz，为保证选取的信号至少包含一个完整周期，共取256个采样点。

通过对该函数进行采样后得到 x1(k)，通过分段插值同步化算法处理后得到 x2(i)后再对其进行FFT变换计算谐波幅值，结果如表1所示。

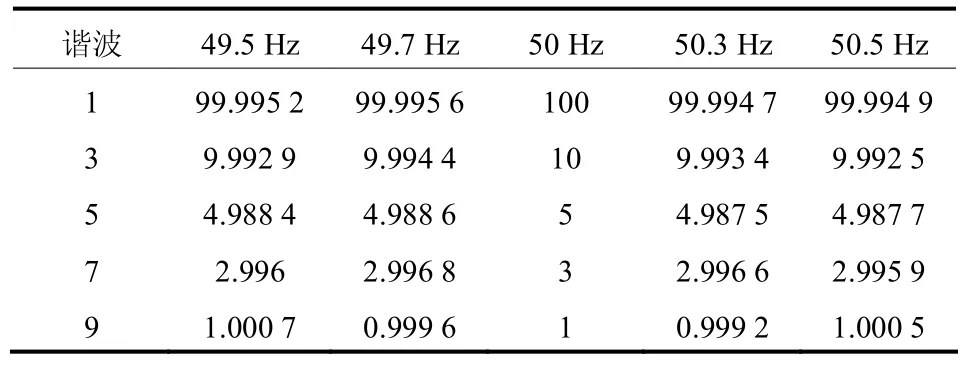
表1 同步化后的幅值仿真结果Table 1 Simulation results of amplitude

由仿真结果可知，在49.5~50.5 Hz的电网基波范围内，该同步化算法在小于等于9次以下的谐波幅值有较高的精度，其相对误差都在0.3%以内，且伴随着谐波次数增加其相对误差并没有明显的增加。

再取f为49 Hz的极端情况，在该情况下分别用线性插值算法、抛物线插值算法、分段插值算法对该信号进行同步化，依旧取采样频率为6 400 Hz，取256个采样点，同步化并FFT变换后结果如表2所示。

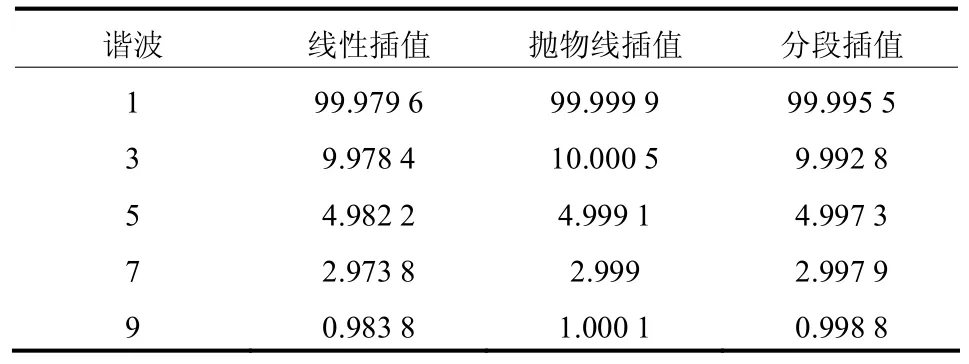
表2 同步化算法的仿真结果对比Table 2 Comparison between simulation results

由表2的仿真结果可得，在49 Hz的情况下，用线性插值算法对非同步信号进行同步化已然产生了一定的误差，其相对误差最大可以达到1.62%，且随着谐波次数的增加，相对误差也有较为明显的扩大趋势；而抛物线插值算法在该情况下精度最高，最大的相对误差也不超过 0.04%，但是相对的，该算法和线性插值相比较为复杂，计算效率不及前者；当使用分段插值算法时，其相对误差最大为0.12%，和线性插值算法对比有了很大改善，满足一般情况下的工程需要，且和抛物线插值对比有更高的计算效率。

3.2 变频率信号仿真分析

由于用电量和发电量处于动态的平衡状态，电网中的实际信号的基频并不是一成不变的，供需关系的实时变化带动着电网频率的变化。此外还存在快速变动的过程信号等非稳态周期信号，其特征即为基波频率在一定范围内波动，只有单周期的测量结果才有实际意义，在这种前提下，对算法的实时性有了较高的要求，且要求对单个周期的采样信号即可进行计算。时域插值法仅需一个完整采样周期即可完成数据的二次同步，能够适用于这种特殊场合。为了更好地对该类信号进行仿真，本文将构造一个频率偏移实时变动的信号对分段插值同步算法进行验证：

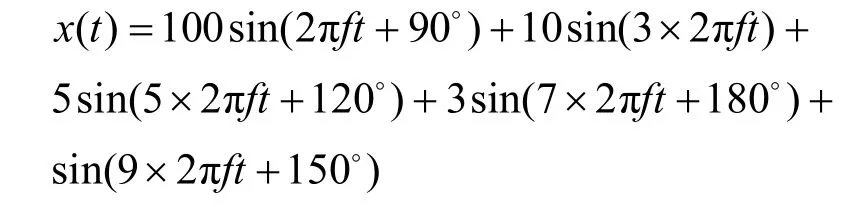
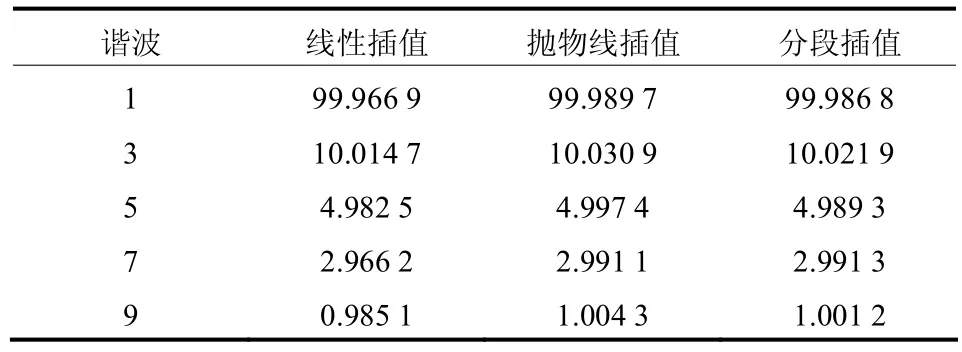
表3 变频信号的仿真结果Table 3 Simulation results of variable frequency signal

由表3可以看出，当用变频率信号对3种不同的插值算法进行验算时，在3次谐波上线性插值算法拥有最高的幅值精度，但是在其他次谐波幅值的计算上其精度明显不及另外两种算法。抛物线插值算法在3次谐波的计算上误差较大，但是在其他谐波幅值的计算上有较高的精度。分段插值算法在低次谐波幅值的计算上和抛物线插值算法精度大致相近，但是在3次谐波和高次谐波的计算中拥有较抛物线插值算法更高的精度，其9次谐波幅值的相对误差仅为0.12%，明显优于另外两种算法。

不妨进一步加大频率的波动范围以模拟微电网等特殊环境下的非稳态周期信号来测试分段插值算法的性能，在信号不变的前提下，设：

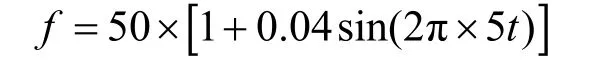
基波频率的变化范围在48~52 Hz，变化的周期为0.2 s。在采样频率为6 400 Hz，256个采样点的前提下对信号进行取样后，用分段插值算法对其进行同步化并FFT后结果如表4所示。

表4 变频信号的仿真结果(2)Table 4 Simulation results of variable frequency signal

由表4结果可见，即使是频率在48~52 Hz的较大范围内以5 Hz波动的非稳态周期信号，仅需要0.04 s的采样，在经过分段插值算法的二次同步化之后，其谐波测量的结果也具有相当的精度。其中相对误差最大的是9次谐波，为1.51%，满足 GBT 17626.7-2008国标要求。该方法适用于对实时性要求较高的非稳态信号检测和电能质量在线快速检测中。

3.3 含高次谐波的信号仿真分析

为了探究该方法对更高次数的谐波的测量精度，有一信号如下：

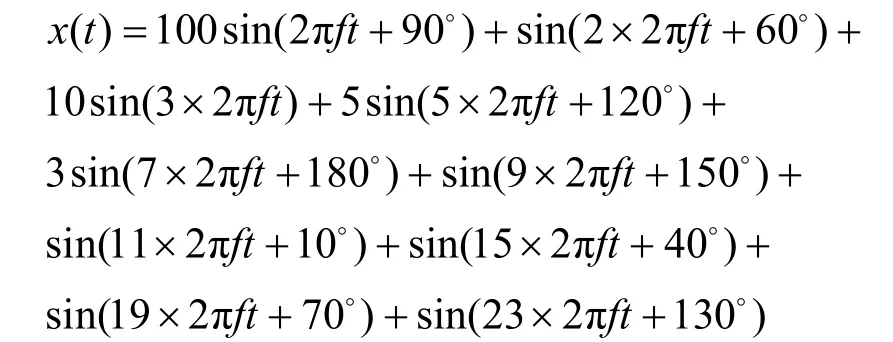
其中，f为49 Hz，仿真时，采样频率为6 400 Hz，取256个采样点。为直观起见，以幅值的相对误差为纵坐标，谐波次数为横坐标绘图如图1所示。

图1 幅值相对误差和谐波次数的关系Fig. 1 Relationship between harmonic order and amplitude error

由图1可见，在9次谐波以后，该方法的精度随着谐波次数增大而逐渐变低，以 GBT 17626.7-2008中的精度要求为准，最高可以测量至23次谐波。这是因为在时域的插值同步化中产生的截断误差等同于原信号引入了噪声，影响了幅值较低的高次谐波的测量。为了改善这一情况，可以选用截断误差更小的插值算法或者在同步化过程中对采样信号进一步细分，但这都将导致算法的复杂化，会降低算法的实时性，在应用中可根据实际需求做出取舍。

4 结论

本文提出了一种基于线性插值和Hermite插值的分段插值算法用来对非同步采样序列进行同步化处理，并对固定频率偏移和变频率偏移两种情况下的非同步序列进行了验算和对比。因为对信号二阶导数绝对值较小的部分采用了计算效率最高的线性插值算法进行拟合，而对信号波峰、波谷附近曲率较大的部分用截断误差高达四阶的两点Hermite插值公式进行计算，理论上只需一个完整周期的采样序列就能进行计算，因此具备了很高的实时性，可以适用于非稳态周期信号的同步化计算和电能质量在线快速检测等场合。仿真结果证明了在基波频率偏移范围很大或者基频偏移连续变化的特殊情况下，该算法依然能满足GBT 17626.7-2008国标的精度要求，是一种有实用价值的非同步取样序列的同步化算法。

[1] 翟瑞淼, 英超, 任国臣, 等. 基于 Nuttall 窗的三峰插值谐波算法分析[J]. 电力系统保护与控制, 2015, 43(10): 38-43. ZHAI Ruimiao, YING Chao, REN Guochen, et al. An approach for harmonic analysis based on Nuttall window and triple-spectral-line interpolation[J]. Power System Protection and Control, 2015, 43(10): 38-43.

[2] 黄冬梅, 龚仁喜, 焦凤昌, 等. 莱夫-文森特窗三谱线插值的电力谐波分析[J]. 电力系统保护与控制, 2014, 42(2): 28-34. HUANG Dongmei, GONG Renxi, JIAO Fengchang, et al. Power harmonic analysis based on Rife-Vincent window and triple-spectral-line interpolation[J]. Power System Protection and Control, 2014, 42(2): 28-34.

[3] 王刘旺, 黄建才, 孙建新, 等. 基于加汉宁窗的 FFT高精度谐波检测改进算法[J]. 电力系统保护与控制, 2012, 40(24): 28-33. WANG Liuwang, HUANG Jiancai, SUN Jianxin, et al. An improved precise algorithm for harmonic analysis based on Hanning-windowed FFT[J]. Power System Protection and Control, 2012, 40(24): 28-33.

[4] 祁才君, 陈隆道, 王小海. 应用插值 FFT算法精确估计电网谐波参数[J]. 浙江大学学报(工学版), 2003, 37(1): 112-116. QI Caijun, CHEN Longdao, WANG Xiaohai. High-accuracy estimation of electrical harmonic parameters by using the interpolated FFT algorithm[J]. Journal of Zhejiang University (Engineering Science), 2003, 37(1): 112-116.

[5] ZHAN G F, GEN G Z, YUAN W. The algorithm of interpolating windowed FFT for harmonic analysis of electric power system[J]. IEEE Transactions on Power Delivery, 2001, 16(2): 160-164.

[6] 蔡忠法, 陈隆道, 周箭. 非同步采样的同步化谐波分析算法[J]. 浙江大学学报(工学版), 2008, 42(4): 682-685. CAI Zhongfa, CHEN Longdao, ZHOU Jian. Synchronizing harmonic analysis algorithm for asynchronous sampling[J]. Journal of Zhejiang University (Engineering Science), 2008, 42(8): 682-685.

[7] 蔡菲娜, 左伍衡. 改进的双速率同步采样法及其傅里叶变换[J]. 浙江大学学报 (工学版), 2005, 39(3): 414-417. CAI Feina, ZUO Wuheng. Improved double-speedsynchronous sampling method and Fourier transform[J]. Journal of Zhejiang University (Engineering Science), 2005, 39(3): 414-417.

[8] 王彭, 周峰, 黄震宇. 基于时域准同步的谐波和间谐波检测算法[J]. 仪器仪表学报, 2013, 34(2): 275-280. WANG Peng, ZHOU Feng, HUANG Zhenyu. Harmonic and interharmonic detection algorithm based on time-domain quasi-synchronous technique[J]. Chinese Journal of Scientific Instrument, 2013, 34(2): 275-280.

[9] XI J T, CHICHARO J F. A new algorithm for improving the accuracy of periodic signal analysis[J]. IEEE Transactions on Instrument and Measurement, 1996, 45(4): 827-830.

[10] 陈隆道, 钱照明, 张圣训. 周期域分析中非同步取样数据的同步化[J]. 电子学报, 2001, 29(7): 1-4. CHEN Longdao, QIAN Zhaoming, ZHANG Shengxun. Synchronization algorithm for the asynchronous sampled data set in period domain signal analysis[J]. Acta Electronica Sinica, 2001, 29(7): 1-4.

[11] HAO Zhenghang, YAO Zhiqing, LI Shaohua, et al. The contribution of double-fed wind farms to transient voltage and damping of power grids[J]. Tehnički Vjesnik, 2015, 22(1): 43-49.

[12] 姚致清, 张茜, 刘喜梅. 基于PSCAD_EMTDC的三相光伏并网发电系统仿真研究[J]. 电力系统保护与控制, 2010, 38(17): 76-81. YAO Zhiqing, ZHANG Qian, LIU Ximei. Research on simulation of a three-phase grid-connected photovoltaic generation system based on PSCAD/EMTDC[J]. Power System Protection and Control, 2010, 38(17): 76-81.

[13] 姚致清, 于飞, 赵倩, 等. 基于模块化多电平换流器的大型光伏并网系统仿真研究[J]. 电力系统保护与控制, 2013, 33(36): 27-33. YAO Zhiqing, YU Fei, ZHAO Qian, et al. Simulation research on large-scale PV grid-connected systems based on MMC[J]. Power System Protection and Control, 2013, 33(36): 27-33.

[14] 周峰, 赵春宇, 黄震宇, 等. 基于时域线性插值的信号周期计算方法及误差分析[J]. 仪器仪表学报, 2011, 32(8): 1724-1730. ZHOU Feng, ZHAO Chunyu, HUANG Zhenyu, et al. Time-domain linear interpolation algorithm and its error analysis for estimating signal period[J]. Chinese Journal of Scientific Instrument, 2011, 32(8): 1724-1730.

[15] 陈隆道, 王小海. 周期域分析中的信号周期算法[J].仪器仪表学报, 2001, 22(4): 410-412. CHEN Longdao, WANG Xiaohai. Period algorithm in period domain in signal analysis[J]. Chinese Journal of Scientific Instrument, 2001, 22(4): 410-412.

[16] 刘洋, 姜守达, 孙圣和. 插值法信号周期测量的精度分析[J]. 电子测量与仪器学报, 2007, 21(1): 6-10. LIU Yang, JIANG Shouda, SUN Shenghe. Accuracy analysis of signal period measurement using interpolation[J]. Journal of Electronic Measurement and Instrument, 2007, 21(1): 6-10.

(编辑 葛艳娜)

Harmonic measurement based on piecewise interpolation synchronization algorithm

WU Chaofan, CHEN Longdao
(College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China)

Due to spectrum leakage, traditional harmonic measurement methods based on FFT lead to a larger error in the measurement of the fundamental frequency offset signal or the unsteady periodic signal. Now this paper uses a method of time domain interpolation to reposition asynchronous sampling sequence, segments sequence and analyze it respectively by using linear interpolation algorithm or Hermite interpolation algorithm according to the sequence of second difference quotient. Then two situations that the fundamental frequency offset is fixed and fundamental frequency is fluctuating are calculated. The results show that piecewise interpolation synchronization algorithm can be applied to the above two cases. Taking computational efficiency into account, it can meet the accuracy requirement of GBT 17626.7 -2008 at the same time. The piecewise interpolation synchronization algorithm is a kind of practical method.

asynchronous sampling; synchronization algorithm; piecewise interpolation algorithm; time-varying signal; spectrum leakage

10.7667/PSPC151078

：2015-07-31

吴超凡(1991-)，男，通信作者，硕士研究生，研究方向为电能质量分析和智能仪器仪表；E-mail: 21310189@ zju.edu.cn

陈隆道(1955-)，男，博士，教授，研究方向为电子测量技术、智能仪器仪表、工程控制。