基于多馈入交互作用因子的直流分区原则和方法研究

徐 蔚，程斌杰，林 勇，徐 政

(1.广东电网有限责任公司电网规划研究中心，广东 广州 510080；2.浙江大学电气工程学院，浙江 杭州 310027)

基于多馈入交互作用因子的直流分区原则和方法研究

徐 蔚1，程斌杰2，林 勇1，徐 政2

(1.广东电网有限责任公司电网规划研究中心，广东 广州 510080；2.浙江大学电气工程学院，浙江 杭州 310027)

运用 VSC-HVDC对多直流馈入系统进行分区能够提升受端系统的运行性能。不同分区方案对系统性能提升程度不同。为了寻找最优方案，运用灵敏度分析法对多直流馈入系统的特性进行了研究，得到了制定分区方案的两个基本原则。在此基础上提出了基于多馈入交互作用因子的直流分区方法，进而得到受端系统分区的最优方案。以广东电网2030水平年作为案例，运用该分区方法对广东电网进行分区，得到了最优分区方案。运用PSS/E进行仿真，验证了该最优分区方案的有效性。该方案对于实际工程中分区方案的制定具有指导意义。

多馈入系统；直流分区；灵敏度分析法；多馈入交互作用因子；分区方法

0 引言

随着直流输电技术的成熟，直流输电在远距离大容量输电工程中得到更为广泛的应用，不可避免同一受端系统会馈入多回直流线路。交直流系统以及直流落点之间复杂的相互作用产生了一系列问题，其中交流系统故障引起多个直流换流站同时发生换相失败的问题一直是广泛研究的课题[1-5]，换相失败导致受端系统瞬时失去大量直流功率，对于交直流并列输电通道，换相失败更会使得潮流大量转移到交流通道而导致整个系统失稳。防止换相失败的一种措施是在交流系统故障期间改变直流系统的控制方式[6-9]，另一种措施是将受端系统分区，减小分区之间的电气耦合程度。受端系统分区可分为同步分区和异步分区，同步分区指分区之间同步运行，通过加装特殊设备增大分区之间电气距离，文献[10]提出了交流联络线上加装故障限流器从而在故障期间减小分区之间耦合的动态分区方法，文献[11]提出利用储能设备对交流系统进行分区的方法，通过储能设备的充放电抑制联络线上的功率摇摆，近似达到直流输电中的定功率控制。然而不管是改变直流系统控制方式还是同步分区，均无法将分区彻底解耦，仍然存在大故障下多个换流站同时发生换相失败的可能性。异步分区通过VSC-HVDC将受端系统分隔成异步运行的小区[12-14](本文称为直流分区)，分区之间基本无耦合，能够彻底防止分区之间换流器同时发生换相失败的问题，随着电力电子技术的发展，直流分区具有更广阔的应用前景。

分析交直流系统稳定特性应着重考虑交直流相互影响作用，并需要引入一系列指标对系统进行描述。文献[15-19]对交直流混合系统的稳定特性进行了研究，文献[20-21]对交直流系统中的有效短路比(ESCR)、最大输送功率(MAP)、系统惯性(Hdc)等指标进行了阐述。对于多直流馈入系统，文献[22-23]对多直流馈入系统的多直流落点短路比(MSCR)与系统稳定性的关系进行了分析，文献[24-25]研究了多馈入交互作用因子(MIIF)的影响因素，文献[26]提出了换相失败抵御因子(CFII)的概念，而文献[27]对描述多直流馈入系统的指标进行了分类整理和分析。多直流馈入系统的特性借助这些指标得到了一定程度上的描述，本文主要依据 MIIF对系统进行描述。多直流馈入系统网架复杂，对指标的计算和分析较为困难，对于多直流馈入系统，采用灵敏度法进行计算分析是一种可行的方法[28-29]，此外文献[30]采用小信号稳定性分析对双直流馈入系统之间的相互影响进行研究。

尽管直流分区已有了相关研究工作，但目前对于直流分区应用于多直流馈入系统的分析，以及在此基础上具体直流分区方法的研究还不多，因此该问题值得深入研究，并且具有实际的工程价值。本文首先对多馈入系统进行建模，并运用灵敏度分析法分析了系统参数对于多馈入交互作用因子的影响，基于以上分析得到了直流分区的两条基本原则；其次本文提出了基于多馈入交互作用因子的直流分区方法以及相应的优化指标，依据直流分区的基本原则得到了直流分区的具体方法和分区流程；最后本文以2030水平年广东电网为例，运用提出的直流分区方法对广东电网的具体分区方案进行研究和分析，得到了最优化方案，通过在PSS/E仿真平台搭建各方案的模型，仿真验证了该方案的可行性和基于多馈入交互作用因子的直流分区方法的有效性。

1 电网直流分区基本架构

直流分区利用柔性直流输电技术(VSC-HVDC)将电网分隔成若干个异步运行的分区电网，多直流落点系统直流分区示意图如图1所示，其中分区之间为柔性直流输电系统，其他为传统直流输电系统(LCC-HVDC)。

图1 电网直流分区基本架构Fig. 1 Basic concept of DC-segmentation

利用电网直流分区技术对多直流落点系统进行分区能有效提升受端系统的运行性能。首先，直流分区将故障的影响范围限制在分区之内，避免了连锁故障引起的大面积停电，有效减少故障下发生换相失败的直流系统数目；其次，柔性直流输电系统能够控制分区之间的潮流交换，有利于电能交易；再次，电网直流分区能够降低受端电网的短路电流水平。

2 多馈入系统描述指标及建模

本文将多馈入交互作用因子(MIIF)作为直流分区的主要依据，并用以评价直流分区的结果。CIGRE B4.41工作组定义了多馈入交互作用因子 MIIF (Multi-Infeed Interaction Factor)[17]，提出的计算式如下

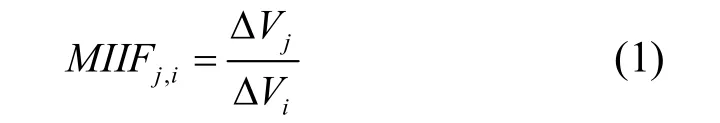
其中：i为自扰动母线；j为观察母线；△Vi为换流站i交流母线的电压扰动量，约为1%；△Vj为换流站j交流母线的电压变化量。

MIIF描述了换流站交流母线之间相互耦合的程度，当两个换流站交流母线完全重合时，耦合最紧密，此时的 MIIF=1；当两个换流站交流母线电气距离无穷远时，相互之间没有耦合，MIIF=0。一般情况下，MIIF介于0和1之间。以双直流馈入系统为例，MIIF矩阵如表1所示。

表1 MIIF矩阵Table 1 Matrix of MIIF

为探究直流分区对系统的影响，本文对双直流馈入等值系统进行分析，主要研究逆变侧，等值系统如图2所示。逆变站1所在分区1和逆变站2所在分区2之间的联络线通过等值阻抗Z34等效，联络线母线分别对应的交流系统采用戴维南法等效成电压源E1、E2和阻抗Z12、Z22。换流站母线与联络线母线之间的等效阻抗用Z11和Z21表示。Bc1、Bc2对应于换流站母线上滤波器和电容器的电纳。注入换流站母线和联络线母线潮流为P11+jQ11、P12+jQ12和P21+jQ21、P22+jQ22。本文依据此双直流馈入模型，利用灵敏度分析法，探究直流分区对多直流馈入受端系统的影响。

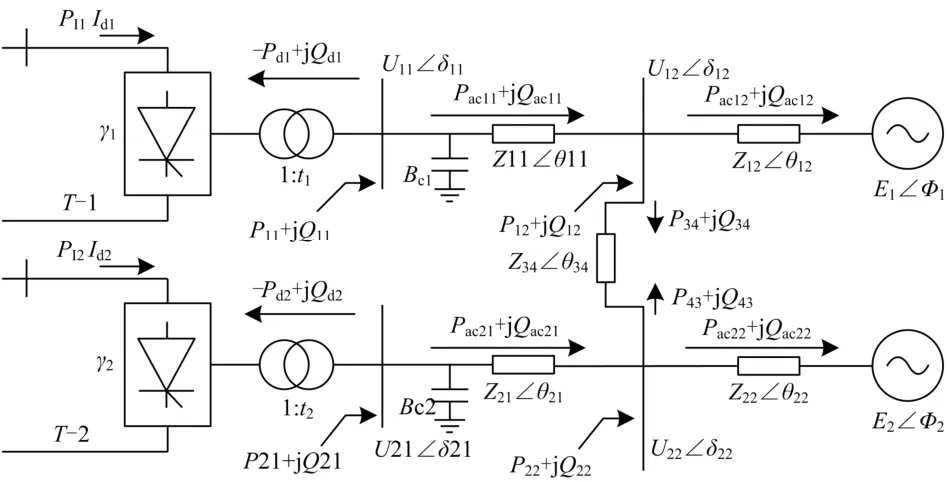
图2 双直流馈入等值系统Fig. 2 Equivalent double-infeed HVDC system

3 分区原则研究

基于灵敏度法，在图2所示模型基础上，研究在系统参数变化情况下，系统多馈入交互作用因子的变化情况，基于以上规律，得到直流分区的基本原则，即1)优先分隔电气耦合程度高(即MIIF值大)的换流站；2)其他条件相同时，优先选择分区短路比较大的方案。这些基本原则对于直流分区流程的制定和实际系统分区方案的确定具有指导作用。

3.1 联络线阻抗对系统的影响

改变联络线等值阻抗Z34的大小，运用灵敏度法进行计算，分析双直流馈入系统中MIIF随联络线阻抗的变化。换流站1和换流站2之间的多馈入交互作用因子MIIF随联络线等效阻抗变化曲线如图3所示。

由图3可以看到，随着联络线等效阻抗Z34的逐步增大，MIIF2,1和MIIF1,2的值逐渐减小，即两个换流站母线之间的电压耦合程度降低，电气距离增大。从物理机理上分析，随着等效联络线阻抗的增加，两个换流站所在分区(分区1和分区2)的电气距离逐渐增大，换流站所处的系统逐渐从强系统变为弱系统。当换流站1母线上出现无功下降时，在等效联络线阻抗较大情况下，该无功更多地由换流站1所在的分区1来承担，而分区2由于联络线阻抗较大，提供的无功相对较少，该区的电压也下降较少，因此换流站之间MIIF较小，同理对于换流站2也是一样。直流分区等效于联络线阻抗趋于很大的值，由图2中曲线的趋势可以看出，对于直流分区，MIIF的值趋于0。

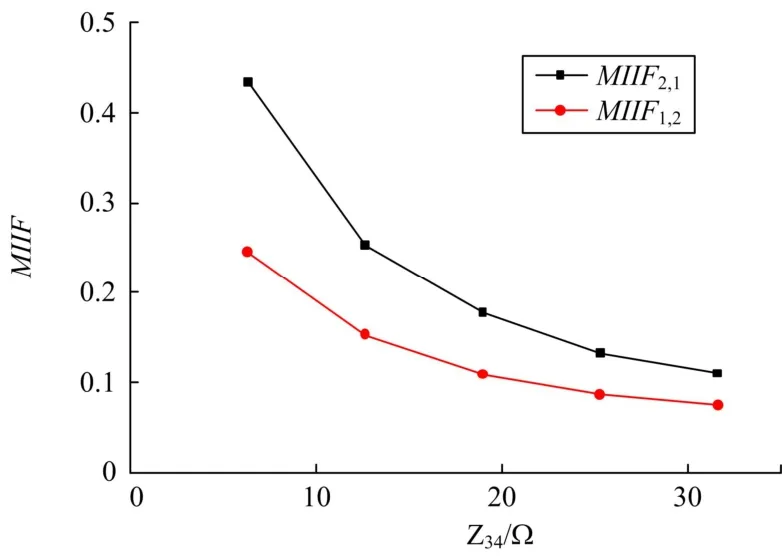
图3 MIIF随联络线等效阻抗变化曲线Fig. 3 Curve of MIIF as impedance of tie line varies

从以上分析可以看出，直流分区有利于隔离换流站之间的故障，即通过分隔换流站对，使得某个换流站附近故障时其他分区内的换流站不受影响，从而有效抑制多条直流线路同时发生换相失败的可能性。在选择分区方案时考虑尽量减小逆变站之间的耦合程度，即减小 MIIF的值，由于直流分区能最大程度减小换流站之间 MIIF的数值，因此在确定分区方案时，优先分隔电气耦合程度高(即 MIIF值大)的换流站。

3.2 等效电源阻抗对系统的影响

同时改变等效电源阻抗 Z12和 Z22的大小(该系统中 Z12=Z22=Z)，运用灵敏度法进行计算，分析双直流馈入系统中 MIIF随等效电源阻抗的变化，如图4所示。

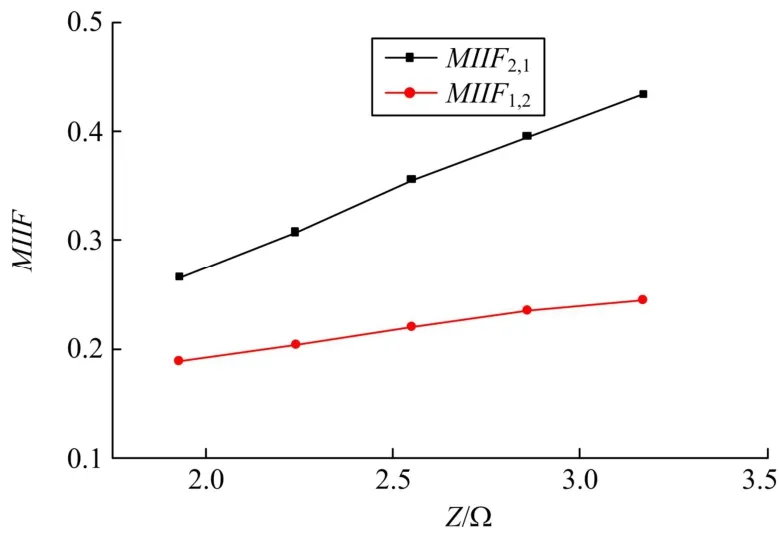
图4 MIIF随等效电源阻抗变化曲线Fig. 4 Curve of MIIF as equivalent source impedance varies

从图4可以直观地看出，随着等效电源阻抗的增大，区内直流换流站母线之间的电压耦合逐渐变强，相互之间的影响增加，因此等效电源阻抗的增大总体上恶化了系统的运行特性。分析物理机理，等效电源阻抗越小，等效电源与换流母线之间的电气距离越短，当换流母线出现无功波动时，电源能够更迅速更多地提供无功以补偿换流母线上的缺额，从而提高电压稳定性，由于该无功波动能够被电源更快地弥补，使得该波动对其他换流母线的影响也相应减小，因此耦合程度下降。

在实际系统中，等效电源阻抗与分区短路比密切相关，等效电源阻抗越小，分区短路比越大，而此时换流站之间耦合程度下降。因此在确定分区方案时，若其他条件差别不大，优先选择分区短路比较大的方案。

4 直流分区方法

包含n个直流换流站的受端等效系统如图5所示。

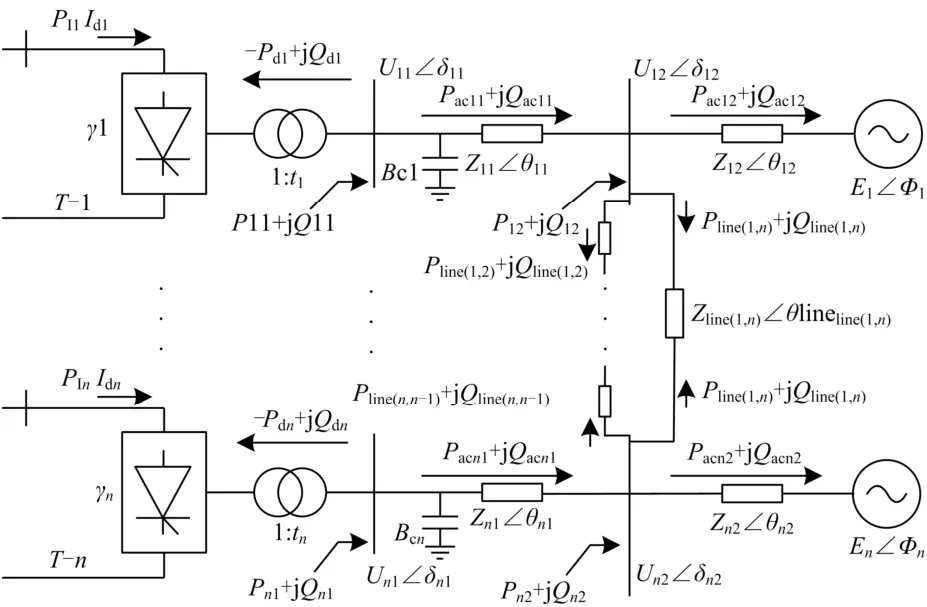
图5 受端等效系统示意图Fig. 5 Equivalent receiving system

依据提出的直流分区的两个原则，从降低换流站之间耦合程度以尽量避免多直流同时换相失败的角度出发，本文提出一种基于 MIIF最优化的直流分区方法，寻找分区后系统MIIF总体最小的方案，即最小化L，如式(2)所示，n为受端系统换流站个数，L反应了各换流站之间的平均耦合程度。

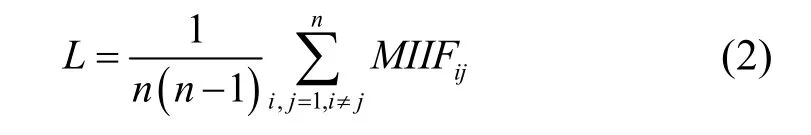
直流分区需要权衡两方面问题：其一，分区后区间换流站耦合程度降低，区间换流站一般不会发生多直流同时换相失败；其二，区内换流站耦合程度上升，区内发生多直流同时换相失败的可能性加大。基于 MIIF最优化的直流分区方法综合考虑了这两方面的因素，以 MIIF来衡量这种耦合程度，最优方案的优化指标为所有换流站之间 MIIF的平均值最小，从而使得受端系统中换流站之间的总体耦合程度下降最多。

以各换流站 MIIF的平均值作为优化指标可以有效避免某个分区内直流数目过多的方案，从而降低更多直流出现同时换相失败的可能性。直流分区后区间换流站的MIIF为0，而区内换流站MIIF有所增大，对于某分区内直流数目过多的方案，MIIF下降为0的换流站对数较少，优化指标L相对较大，使得该方案更不易被选择，从而有效避免了该问题。另外考虑到联络线数目最少和行政划分等原因，分隔两个特定的换流站时，加装VSC-HVDC换流站的联络线是确定的。

值得注意的是，也可以从小到大排列优化指标L，选择 L较小的若干个方案作为最优分区方案，在考虑各类实际因素的情况下进一步进行规划。本文选择一个最优分区方案为例。

基于MIIF最优化的直流分区方法主要分两步进行。

4.1 选择候选方案

由于受端系统换流站个数较多，分区方案也相应较多，在优化指标L下如果对每个方案进行一一计算，则过程复杂且工作量大，因此首先选择候选方案。候选方案选择的整体思路是优先分隔耦合程度高的换流站，一方面耦合程度高的换流站极有可能同时发生换相失败，另一方面由于被分隔换流站MIIF为0，分隔耦合程度高的换流站能更大程度地降低优化指标 L。结合以上两方面，候选方案最大程度地包括了分区的最优方案。

一般情况下，对于换流站 i和换流站 j，MIIFi,j≠MIIFj,i。在选择候选方案时取

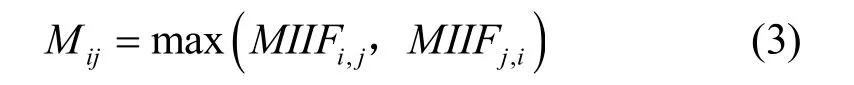
选择候选方案时，首先求出受端系统各个换流站的MIIF矩阵，根据式(3)得到每对换流站的Mij。Mij反应了换流站之间的耦合程度，本文称Mij为换流站耦合程度因子，从大到小对 Mij进行排序，即按耦合程度对每对换流站进行排序。

其次选择换流站耦合程度因子Mij中前k对换流站作为候选分隔对象，k根据实际情况而定。若须将受端系统分成j个异步网，则从k对换流站中选择j对作为被分隔对象，即候选方案，共有种。例如，对于有10个直流换流站的受端系统，Mij共有45个，从高到低取前5个Mij，即k=5。若分成3个异步网，则共有10种候选方案。

考虑特殊情况：对于三个相邻换流站i、i+1、i+2，如果选取的前k个换流站耦合程度因子中同时包括Mi,i+1，Mi,i+2，即分隔换流站i和(i+1)的同时也分隔了换流站i和(i+2)，此时把Mi,i+1和Mi,i+2分别对应的换流站对视为一个换流站对，即分隔换流站i和(i+1)，同时再增加第(k+1)个换流站耦合程度因子对应的换流站对作为候选分隔对象。

最后，对候选方案进行补充。以上得到的候选分区方案中，假设方案1和方案2各分区内直流换流站数目相同，根据4.2节结果，如果分区内对应短路比较小，则分区内换流母线电压稳定性较低，区内换流站耦合程度较高，因此对于分区短路比较小的候选方案，可考虑进一步剔除以减少工作量，具体如式(4)和式(5)所示，如果式(5)成立，则剔除分区短路比较小的方案，即对于式(4)，若H1,2>0，剔除方案2，若H1,2<0，剔除方案1。

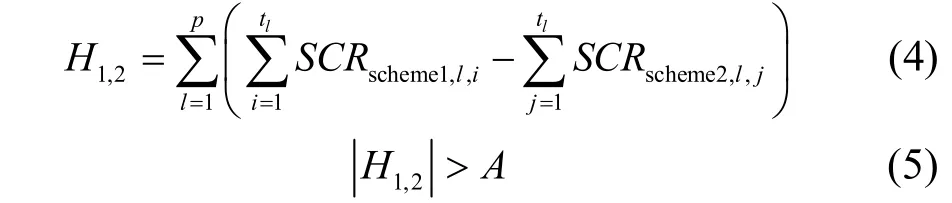
其中：p为分区数目；tl为区内换流站个数，l为分区编号；A为阈值；SCR为换流站对应的短路比。

4.2 确定最优方案

对每一种候选方案进行直流分区，相应地求出每种方案下的MIIF矩阵，并计算式(2)，得到优化指标L最小的方案即为最优的直流分区方案。基于MIIF最优化的直流分区方法的流程图如图6所示。

5 直流分区案例

以南方电网2030年规划方案为例，基于MIIF最优化对广东省进行直流分区(方案中广东电网与南方电网主网异步运行)。广东省内共有10个直流落点，如图7所示。

5.1 选择候选方案

利用 PSS/E仿真平台，计算各换流站之间MIIF，从大到小得到换流站耦合程度因子 Mi,j，取前 4对换流站作为候选分隔对象，分别为 M1,10= 0.656 9，M5,7=0.327 9，M8,9=0.314 0，M6,7= 0.255 9。各换流站编号如图6所示。依据4.1节，对于M5,7和M6,7，分隔换流站6和7即可，此时根据Mi,j大小引入下一个换流站耦合程度因子 M5,6=0.199 5。从而得到候选分隔对象为：乌东德直流和贵广直流II换流站对、伊江直流III和溪洛渡直流换流站对、云广直流I和三广直流换流站对、天广直流和伊江直流III换流站对。

将广东电网分隔成两个异步网，则共有6种方案，其中方案a：分隔乌东德直流、贵广直流II换流站对和云广直流I、三广直流换流站对，方案b：分隔伊江直流III、溪洛渡直流换流站对和云广直流I、三广直流换流站对，这两种方案均将广东电网分成了分别含有2个和8个换流站的两个分区，根据分区流程，计算两种方案中各换流站的短路比，如表2所示。

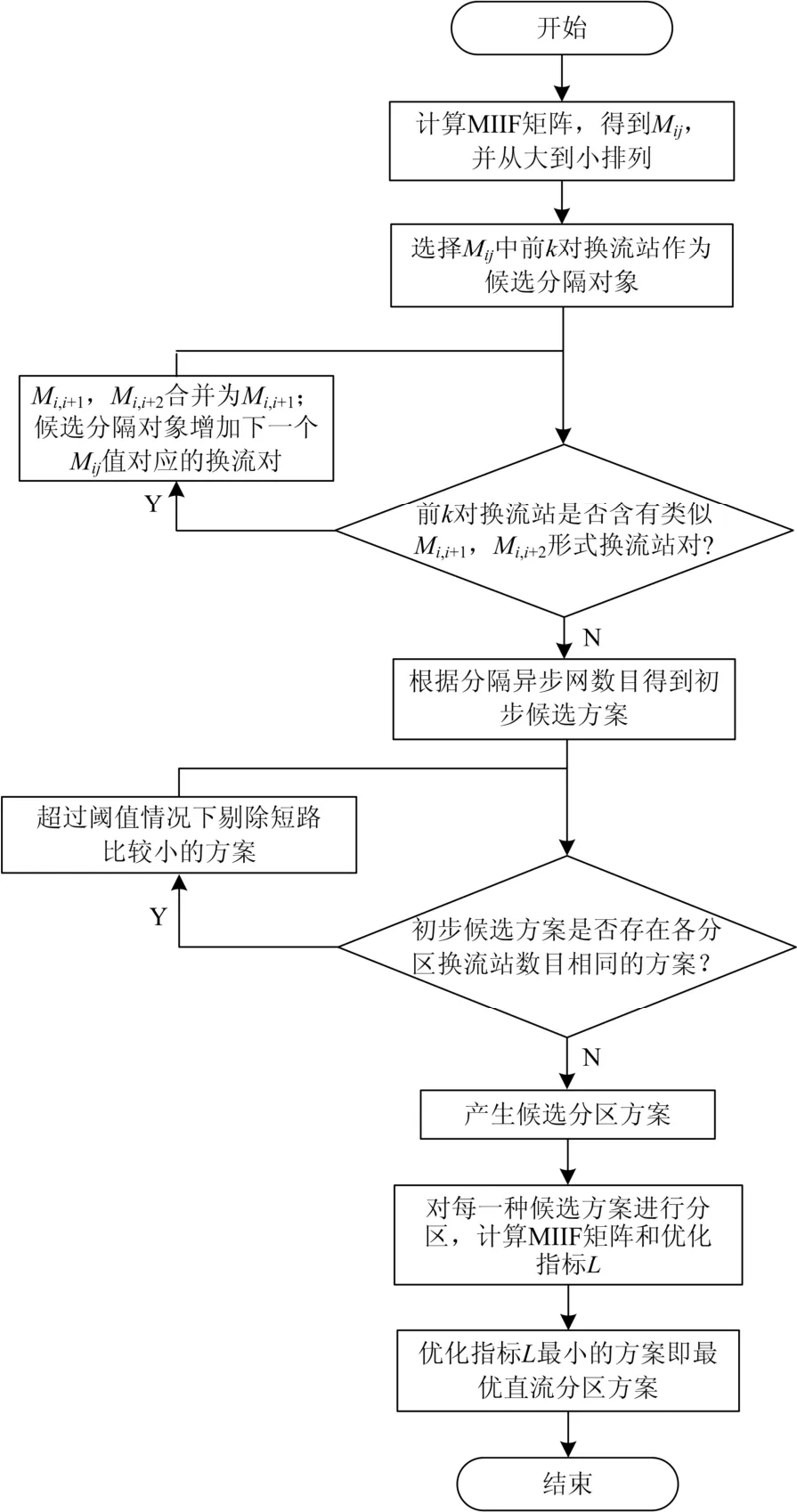
图6 基于MIIF最优化的直流分区方法流程图Fig. 6 Flow chart of the DC-segmentation method

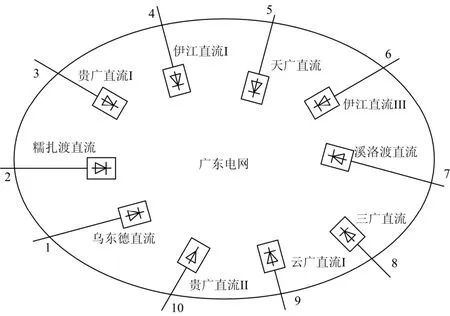
图7 2030年广东电网直流落点分布Fig. 7 DC terminal location of projected Guangdong grid in 2030

根据式(4)和式(5)，本文阈值A取0，由表2，Ha,b=-15.158 5<0，因此剔除方案a。

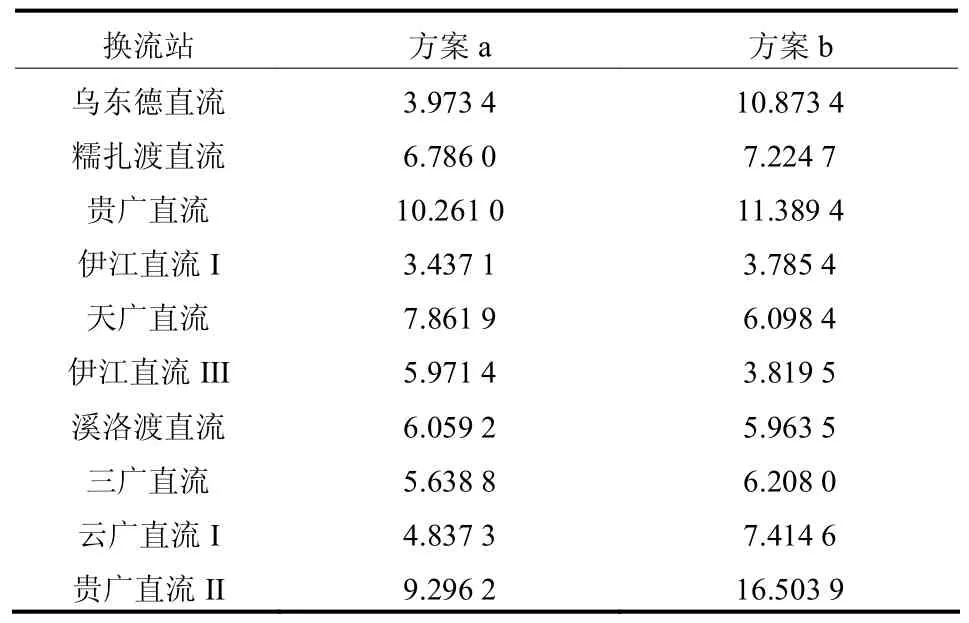
表2 两方案各换流站短路比Table 2 SCR of two schemes

综上得到5种候选分区方案，如表3所示。

表3 候选分区方案Table 3 Candidate DC-segmentation schemes

5.2 确定最优方案

依照候选方案，在 PSS/E仿真平台上用VSC-HVDC柔性直流输电技术对广东电网进行分区，将广东电网分隔成两个异步网，并计算分区后广东电网的MIIF矩阵。根据式(2)，利用MIIF矩阵计算得到每种候选方案的优化指标L，如表4所示。

表4 各候选方案优化指标LTable 4 Index L of each candidate scheme

分析表 4，可以得到以下三点。a. 各候选方案与未分区方案进行比较，直流分区后优化指标L显著下降，说明各换流站之间的平均耦合程度下降，分区是合理有效的。b. 方案1和方案2优化指标L较小，这是因为这两个方案分隔的两个异步区内换流站数目较为均衡，更多的换流站对通过背靠背VSC-HVDC隔开了，换流站之间的总体耦合程度下降。c. 方案4的优化指标L最大，该方案的1个分区中只有一个直流换流站伊江直流III，另外9个换流站分布在另一分区中，从而很有可能引起更多换流站同时发生换相失败，从技术和经济上该方案都较为不合理，因此方案4的优化指标L最大，即最不可能被选中作为最终方案。

表4中，方案2的优化指标L最小，因此确定该方案为分区最终方案。在方案2中，分隔的两个分区内各有5个换流站，有效降低了更多换流站同时发生换相失败的可能性。相比于其他方案(某一分区内换流站数目较少)，某些故障下该方案可能会有更多换流站换相失败，但是从总体上分析，即考虑系统各个换流站之间的总体耦合程度，该方案是最优的。

5.3 仿真验证

5.3.1 换流母线故障仿真

考查换流母线故障，基于PSS/E仿真平台，对于每个候选方案，系统运行至1.00 s时换流母线发生短路故障，1.10 s后故障切除，统计广东电网内发生换相失败换流站的个数，以及每个候选方案在最严重故障下广东电网损失的最大直流功率，如表5所示。

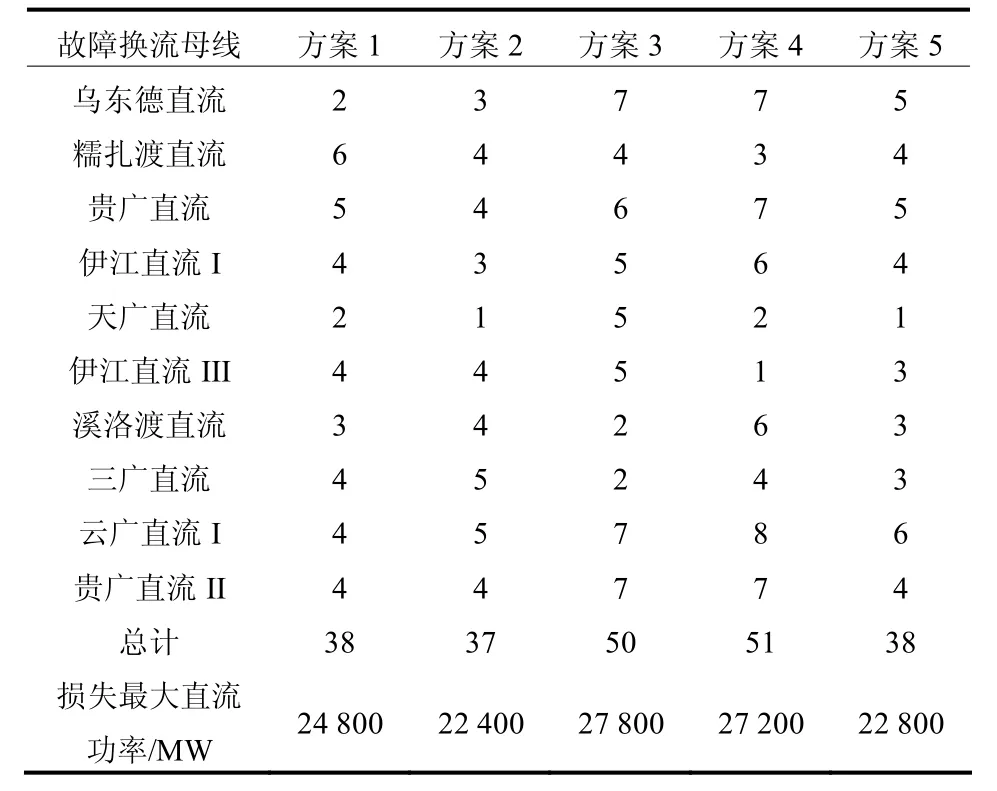
表5 换相失败换流站统计以及损失最大直流功率Table 5 Number of DC inverters suffering commutation failure and the maximum DC power loss of the grid

分析表 5，可以得到以下两点。第一，当每条换流母线发生短路故障时，方案2中发生换相失败换流站的总和最少，即每个故障下发生换相失败换流站的平均个数最少；分析最严重换流母线故障下广东电网内失去的最大直流功率，可以看到方案 2最少。综合以上两点，方案2的分区方案电网在故障下稳定性高，为最优方案。

第二，大区大故障，小区小故障。本文中大区指换流站数目较多的分区，小区指换流站数目较少的分区。例如当伊江直流III换流母线发生短路故障时，对于方案4该故障在其小区内，该区内所有换流站发生换相失败，即便如此，总共只有1个换流站(即该换流站)换相失败；而当云广直流I换流母线发生故障，由于该故障位于方案4的大区内，更多换流站发生了换相失败，总共有8个，更多有功功率的瞬间缺失加大了系统崩溃的可能性。另外方案3也有类似现象，由表5可看出这些方案在最严重故障下失去的最大直流功率也较多。这些分区方式在某些故障下发生换相失败的换流站数目较多，瞬间失去较多直流功率，对系统的安全稳定运行影响大，由第5节分析，这些分区方案的优化指标L也相应较大，被选择为最终方案的可能性相对较小，这也验证了本文分区方法的有效性。

5.3.2 线路故障仿真

考虑到故障发生的随机性，在受端系统中按区域的分布平均选取11条双回线路，基于PSS/E仿真平台分别作故障仿真，即1.00 s时一回线路发生三相短路故障，1.10 s时切除该回线路，并统计系统中发生换相失败的换流站数目。在每种候选方案下，11条双回线路分别发生故障时，换相失败的换流站数目统计如表6所示。

表6 换相失败换流站数目统计Table 6 Number of DC inverters suffering commutation failure

分析表6，尽管在某些线路故障下方案2发生换相失败的换流站数目多于某些其他的方案，但考察所有选择线路分别故障下发生换相失败的换流器数目之和，则方案2的数目比其他分区方案少，说明方案2是总体最优的方案，这种分区方案是合理的。

另外可以看到，大区系统较强，远离换流站的线路故障时发生换相失败的换流站数目少。一般情况下大区内换流站对应等效系统的短路比较大，由4.2节分析可以看出，此时各换流站换流母线的互相耦合程度下降。当故障发生点距离换流站较近时，电压跌落较大，多条直流必然发生换相失败；而当故障发生点距离较远时，由于大区内电压稳定性高，换流母线耦合程度低，各换流站换流母线上电压跌落反而较低，发生换相失败的换流站较少。例如，当奥里油-湛北单回线路发生故障时，由于该线路与各个换流站电气距离较远，尽管方案3和方案4分区内换流站较多，但发生换相失败的换流站数目相对较少。反过来看，小区由于电压稳定性低，换流站耦合程度较高，电气距离相对较远的故障同样会导致较多换流站发生换相失败。而由本案例可以看出，本文选择的分区方案中没有出现分区换流站数目较少的情况，最大程度上降低换流母线之间的耦合程度。从这个角度分析，本文提出的分区方法同样具有合理性。

6 结论

1) 本文运用灵敏度分析法，研究了多直流馈入系统 MIIF分别与联络线阻抗和等效电源阻抗的关系，进而得到了指导直流分区方案制定的两条基本原则：a. 优先分隔电气耦合程度高(即 MIIF值大)的换流站；b. 其他条件相同时，优先选择分区短路比较大的方案。

2) 本文提出了基于多馈入交互作用因子的直流分区方法，给出了方案的优化指标L和相应的分区流程图，即首先选择分隔 MIIF较大的换流站对作为候选方案，其次通过计算候选方案的优化指标L得到最优方案。

3) 本文使用该分区方法为实际电网制定直流分区方案，得到了最优分区方案，同时利用 PSS/E对交流侧故障时发生换相失败的换流站数目进行仿真，验证了分区方法的有效性。

4) 基于多馈入交互作用因子的直流分区方法为电网分区规划提供了指导，工程中可以通过该方法得到若干个最优方案，在考虑各类实际因素下得到最终方案。

[1] 林凌雪, 张尧, 钟庆, 等. 多馈入直流输电系统中换相失败研究综述[J]. 电网技术, 2006, 30(17): 40-46. LIN Lingxue, ZHANG Yao, ZHONG Qing, et al. A survey on commutation failures in multi-infeed HVDC transmission systems[J]. Power System Technology, 2006,30(17): 40-46.

[2] 王海军, 黄义隆, 周全. 高压直流输电换相失败响应策略与预测控制技术路线分析[J]. 电力系统保护与控制, 2014, 42(21): 124-131. WANG Haijun, HUANG Yilong, ZHOU Quan. Analysis of commutation failure response strategies and prediction control technology in HVDC[J]. Power System Protection and Control, 2014, 42(21): 124-131.

[3] 郭启伟, 赵建国, 牛林, 等. 银东±660 kV 直流系统故障的动态特性仿真研究[J]. 电力系统保护与控制, 2012, 40(11): 133-139. GUO Qiwei, ZHAO Jianguo, NIU Lin, et al. Fault simulation of dynamic characteristics about ±660 kV Yindong HVDC system[J]. Power System Protection and Control, 2012, 40(11): 133-139.

[4] 肖浩, 裴泽阳, 高桂革, 等. 浅析柔性直流输电关键技术及其前景展望[J]. 电器与能效管理技术, 2015(13): 32-38. XIAO Hao, PEI Zeyang, GAO Guige, et al. Analysis on the key technologies for VSC-HVDC and its prospect[J]. Electrical & Energy Management Technology, 2015(13): 32-38.

[5] 陈干, 田方, 刘宁, 等. 高压直流输电工程换相失败研究[J]. 高压电器, 2015, 51(7): 136-140, 147. CHEN Gan, TIAN Fang, LIU Ning, et al. Research on HVDC transmission project commutation failure[J]. High Voltage Apparatus, 2015, 51(7): 136-140, 147.

[6] HANSEN A, HAVEMANN H. Decreasing the commutation failure frequency in HVDC transmission systems[J]. IEEE Transactions on Power Delivery, 2000, 15(3): 1022-1026.

[7] 袁阳, 卫志农, 王华伟, 等. 基于直流电流预测控制的换相失败预防方法[J]. 电网技术, 2014, 38(3): 565-570. YUAN Yang, WEI Zhinong, WANG Huawei, et al. A DC current predictive control based method to decrease probability of commutation failure[J]. Power System Technology, 2014, 38(3): 565-570.

[8] 颜泉, 李兴源, 刘红超, 等. 多馈入交直流系统关联测量分散协调控制[J]. 电工技术学报, 2004, 19(12): 42-46, 52. YAN Quan, LI Xingyuan, LIU Hongchao, et al. Decentralized coordinated control of multi-infeed HVDC based on correlative measured vectors[J]. Transactions of China Electrotechnical Society, 2004, 19(12): 42-46, 52.

[9] 朱泽安, 刘巍, 姚晓君. 一种适用于电压源型换流器多端直流输电系统的协调控制策略[J]. 电器与能效管理技术, 2014(13): 34-38. ZHU Zean, LIU Wei, YAO Xiaojun. Coordinated control strategy for voltage source converter multi-terminal high voltage DC Transmission system[J]. Electrical & Energy Management Technology, 2014(13): 34-38.

[10] 黄弘扬, 徐政, 林晞. 基于故障限流器的直流多馈入受端系统动态分区技术[J]. 中国电机工程学报, 2012, 32(19): 58-64, 186. HUANG Hongyang, XU Zheng, LIN Xi. Fault current limiters based dynamic segmentation technique for multi-infeed HVDC systems[J]. Proceedings of the CSEE, 2012, 32(19): 58-64, 186.

[11] 吴晋波, 孙海顺, 文劲宇, 等. 利用储能技术实现交流互联电网分区解耦控制的可行性研究[J]. 中国电机工程学报, 2011, 31(16): 8-13. WU Jinbo, SUN Haishun, WEN Jinyu, et al. Feasibility study of region decoupling control for AC interconnected grids using energy storage technology[J]. Proceedings of the CSEE, 2011, 31(16): 8-13.

[12] CLARK H, EDRIS A A, EL-GASSEIR M, et al. Softening the blow of disturbances[J]. IEEE Power and Energy Magazine, 2008, 6(1): 30-41.

[13] FANG Xinghao, CHOW J H. BTB DC link modeling, control, and application in the segmentation of AC interconnections[C] // Proc 2009 IEEE Power & Energy Society General Meeting (PES), 2009.

[14] 姚致清, 赵倩, 刘喜梅. 基于准同步原理的逆变器并网技术研究[J]. 电力系统保护与控制, 2011, 39(24): 123-126, 131. YAO Zhiqing, ZHAO Qian, LIU Ximei. Research on grid-connected technology of inverter based on quasi synchronous principle[J]. Power System Protection and Control, 2011, 39(24): 123-126, 131.

[15] 于春光, 陈青, 高湛军. 计及直流接入的交流系统故障计算模型研究[J]. 电力系统保护与控制, 2013, 41(3): 1-7. YU Chunguang, CHEN Qing, GAO Zhanjun. A fault analysis model for AC system interconnected by HVDC system[J]. Power System Protection and Control, 2013, 41(3): 1-7.

[16] 贾俊川, 赵兵, 罗煦之, 等. 青藏直流投运后藏中电网稳定特性研究[J]. 电力系统保护与控制, 2014, 42(6): 104-109. JIA Junchuan, ZHAO Bing, LUO Xuzhi, et al. Research on the security and stability characteristics of Central Tibet power grid after Qinghai-Tibet HVDC putting into operation[J]. Power System Protection and Control, 2014, 42(6): 104-109.

[17] 徐蔚, 黄弘扬, 徐政. PSS/E的直流模型及与BPA直流系统响应特性的比较[J]. 高压电器, 2013, 49(12):116-122. XU Wei, HUANG Hongyang, XU Zheng. Modelling HVDC systems in PSS/E and comparison of HVDC response characteristics in PSS/E and BPA[J]. High Voltage Apparatus, 2013, 49(12): 116-122.

[18] 陈虎, 贺洋, 张英敏, 等. 四川电网多送出直流输电系统交互影响分析[J]. 电力系统及其自动化学报, 2013, 23(4): 21-26. CHEN Hu, HE Yang, ZHANG Yingmin, et al. Interaction analysis of multi-send HVDC systems of Sichuan power grid[J]. Proceedings of the CSU-EPSA, 2013, 23(4): 21-26.

[19] 李生福, 张爱玲, 李少华, 等. “风火打捆”交直流外送系统的暂态稳定控制研究[J]. 电力系统保护与控制, 2015, 43(1): 108-114. LI Shengfu, ZHANG Ailing, LI Shaohua, et al. Study on transient stability control for wind-thermal-bundled power transmitted by AC/DC system[J]. Power System Protection and Control, 2015, 43(1): 108-114.

[20] GAVRILOVIC A. AC/DC system strength as indicated by short circuit ratios[C] // AC and DC Power Transmission, 1991. International Conference on, IET, 1991: 27-32.

[21] 郭小江, 汤涌, 郭强, 等. CIGRE 多馈入直流短路比指标影响因素及机理[J]. 电力系统保护与控制, 2012, 40(9): 69-74, 81. GUO Xiaojiang, TANG Yong, GUO Qiang, et al. Influence factors and theory for CIGRE MISCR index[J]. Power System Protection and Control, 2012, 40(9): 69-74, 81.

[22] 林伟芳, 汤涌, 卜广全. 多馈入交直流系统短路比的定义和应用[J]. 中国电机工程学报, 2008, 28(31): 1-8. LIN Weifang, TANG Yong, BU Guangquan. Definition and application of short circuit ratio for multi-infeed AC/DC power systems[J]. Proceedings of the CSEE, 2008, 28(31): 1-8.

[23] 井艳清, 尹成竹, 王淼, 等. 整流站与逆变站临近的多直流系统短路比分析[J]. 电力系统及其自动化学报, 2014, 26(6): 25-29. JING Yanqing, YIN Chengzhu, WANG Miao, et al. Analysis of short circuit ratio of rectifier station near the inverter station system with multiple HVDC links[J]. Proceedings of the CSU-EPSA, 2014, 26(6): 25-29.

[24] 陈修宇, 韩民晓, 刘崇茹. 直流控制方式对多馈入交直流系统电压相互作用的影响[J]. 电力系统自动化, 2012, 36(2): 58-63. CHEN Xiuyu, HAN Minxiao, LIU Chongru. Impact of control modes on voltage interaction between multi-infeed AC-DC system[J]. Automation of Electric Power Systems, 2012, 36(2): 58-63.

[25] 汪惟源, 杨林, 史慧杰, 等. 多馈入交互因子在多馈入交直流电网中的应用[J]. 电网与清洁能源, 2015, 31(4): 54-58, 65. WANG Weiyuan, YANG Lin, SHI Huijie, et al. Application of multi-infeed interaction factor in multi-infeed AC/DC hybrid power grid[J]. Power System and Clean Energy, 2015, 31(4): 54-58, 65.

[26] RAHIMI E, GOLE A M, DAVIES J B, et al. Commutation failure analysis in multi-infeed HVDC systems[J]. IEEE Transactions on Power Delivery, 2011, 26(1): 378-384.

[27] AIK D L H, ANDERSSON G. Analysis of voltage and power interactions in multi-infeed HVDC systems[J]. IEEE Transactions on Power Delivery, 2013, 28(2): 816-824.

[28] ZHANG X, CHEN C. Maximum available power of multi-infeed HVDC system analysed by sensitivity method[J]. IET Generation, Transmission & Distribution, 2014, 8(3): 473-479.

[29] FRANKEN B, ANDERSSON G. Analysis of HVDC converters connected to weak AC systems[J]. IEEE Transactions on Power Systems, 1990, 5(1): 235-242.

[30] KARAWITA C, ANNAKKAGE U D. Multi-infeed HVDC interaction studies using small-signal stability assessment[J]. IEEE Transactions on Power Delivery, 2009, 24(2): 910-918.

(编辑 葛艳娜)

DC-segmentation planning based on multi-infeed interaction factor

XU Wei1, CHENG Binjie2, LIN Yong1, XU Zheng2
(1. Grid Planning & Research Center, Guangdong Power Grid Corporation, Guangzhou 510080, China 2. College of Electrical Engineering, Zhejiang University, Hangzhou 310027, China)

The operating performance of receiving terminal power system can be improved by segmenting a multi-infeed HVDC system into a set of asynchronously operated DC-interconnected sectors using VSC-HVDC. Different DC-segmentation schemes have different impact on multi-infeed system. In order to figure out the optimal scheme, this paper firstly analyzes the characteristics of multi-infeed systems by sensitivity method and puts forward two principles of DC-segmentation. Secondly according to these principles, a DC-segmentation method based on multi-infeed interaction factor is presented and then the optimal scheme of receiving terminal power system partition is got. Finally, by applying the method, an actual large scale network is studied and the optimal DC-segmentation scheme is obtained. The effectiveness of the optimal scheme and the DC-segmentation method is verified through simulations on PSS/E. This paper has guiding significance for making DC-segmentation schemes in real projects.

multi-infeed system; DC-segmentation; sensitivity method; multi-infeed interaction factor; DC-segmentation method

10.7667/PSPC151071

：2015-09-11

徐 蔚(1984-)，男，硕士，高级工程师，研究方向为电力系统规划与分析；E-mail：xuwei@gd.csg.cn

程斌杰(1990-)，男，硕士研究生，研究方向为大规模交直流电力系统分析；

林 勇(1973-)，男，硕士，高级工程师，研究方向为电力系统规划与分析。