改进的稀疏表示图像超分辨率复原算法

邱大伟，刘彦隆

(太原理工大学 信息工程学院，山西 太原030024)



改进的稀疏表示图像超分辨率复原算法

邱大伟，刘彦隆

(太原理工大学 信息工程学院，山西 太原030024)

摘要:针对信号的稀疏分解特征，结合图像的超分辨率复原的特点，提出了基于稀疏表示的图像超分辨率复原算法，对两个过完备字典的训练过程、稀疏表示复原算法处理过程进行阐述，同时对改进算法中采用的优化的特征提取算法和自适应边缘方向插值优化低分辨率图像的初始估计两个过程进行详细描述，并通过MATLAB对其进行仿真和验证，实验结果表明，改进算法的复原效果进一步提高，图像细节能够得到恢复，获得更好的鲁棒性。

关键词:稀疏表示；特征提取；边缘插值

超分辨率图像复原一直是一个热门研究对象，它解决的是不改变硬件的条件下改善图像质量的同时重建成像系统截止频率之外的信息的问题。超分辨率复原算法主要分为基于重建的方法和基于学习的方法，基于重建的方法主要是要获取一个精确的图像获取模型，人为地构造高分辨率图像的先验约束，低分辨率图像由模型估计出高分辨率图像，比较经典的算法就是POCS算法，文献[1]就是利用POCS算法进行图像超分辨率重建，论文中复原算法包括3个部分：构造参考帧、进行运动估计和对参考帧进行修正；文献[2]将改进后的小波融合技术运用到运动模糊图像复原中，算法的思想是将Randon变换和微分自相关法巧妙地结合起来得到模糊尺度，再利用小波融合技术进行复原，得到了较好的图像边缘细节信息。由于重建方法的先验约束人为操作因素较大，重建灵活性不高，所以提出了基于学习的重建算法，用学习过程获得先验知识，取代重建中人为定义的平滑约束项，因为不同图像在高频细节上具有相似性，所以通过学习算法获得大量图像高分辨率和低分辨率之间的关系，对于输入的低分辨率图像利用这种关系就能得到高分辨率图像，由William T.Freeman提出的利用马尔科夫随机场实现的基于示例学习的超分辨率复原算法是比较经典的学习复原算法，如文献[3]，Freeman通过大量的输入高分辨率图像训练得到高低分辨率匹配对作为学习字典，利用KD树算法检索补丁对，再通过置信传播算法进行全局能量优化，最终得到复原图像；文献[4]提出的稀疏混合估计的方法实现图像超分辨率复原，通过正交匹配追踪减少混合系数的计算，利用稀疏小波混合插值实现图像复原；文献[5]提出的利用非局部自回归模型进行稀疏表示的图像超分辨率复原，算法利用非局部自回归矩阵S、权重矩阵λ和η、PCA字典ψ不断更新当前图像估计x，通过最小化能量函数进行图像的超分辨率复原；文献[6]寻找每一个输入低分辨率块的稀疏表示，通过这个稀疏表示系数和过完备字典来生成高分辨率图像，过完备字典是通过学习训练库中高分辨率和低分辨率图像的对应关系得到的。

本文算法是在文献[6]算法上的改进，改进过程分为以下两个部分：1)二维特征提取的改进；2)用边缘方向插值代替双三次插值作为高分辨率图像的初始估计。

1图像降质的稀疏表示

设X为高分辨率图像，Y为低分辨率图像，x为X的图像块，y为Y的图像块，则x与y之间有如下关系

y=Lx=LDα

(1)

式中：L为投影矩阵，D为过完备字典，α为稀疏表示。

构造两个字典：高分辨率字典Dh和低分辨率字典Dl，对于每一个高分辨率图像块和低分辨率图像块有相同的稀疏表示。

高分辨率图像块x可以通过高分辨率字典Dh和稀疏表示α得到

x≈Dhα

(2)

稀疏表示α是通过低分辨率图像块y和低分辨率字典Dl得到的，所以组合所有的图像块x即得到复原的高分辨率图像块。

主要的问题就是稀疏表示α的确定，用式(3)来计算

(3)

式中：F为特征提取，后面章节将介绍F的获得过程。

为了使得到的稀疏表示α更加稀疏，用l1范数代替0范数，如

(4)

求解式(5)即可得

(5)

以上算法是经典图像稀疏表示模型，但是算法存在一个主要的问题：没有考虑图像块之间的关系，所以考虑到邻近图像块的相关性，设置了图像块之间的重叠区域，式(4)可写成

min‖α‖1

(6)

式中：P为复原区域与复原区域的重叠部分，ω为重叠部分中之前复原部分。进一步得到

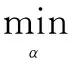
(7)

解此式即得到稀疏表示а，进一步可得到高分辨率图像X。

2稀疏表示的图像复原

低分辨率图像Y可以由高分辨率图像X通过模糊和下采样得到，即

Y=SHX

(8)

式中：H为模糊滤波器。

稀疏表示的图像复原过程就是求式(9)的过程

(9)

式中：X0为通过稀疏表示得到的高分辨率图像；X*为最终的高分辨率图像。

完整的算法流程图如图1所示。

3过完备字典学习算法

影响稀疏表示复原效果好坏的一个主要因素是字典的选择，字典通常可以通过两种方法得到：1)由已知的信号变换构造出字典，如小波变换、Contourlet变换等；2)由给定的训练数据进行学习构造出字典，如K-SVD树字典学习算法、在线字典学习算法等[7]。

过完备字典学习算法被广泛用于信号的稀疏表示中，字典学习算法首先从训练数据开始，设M为一组训练数据，把M放入一个N×L的矩阵中，即M∈RN×L,通过字典训练求的字典D∈RN×L和对应的稀疏表示α∈RN×L，这时要满足约束条件即保证信号残差ε=M-Dα和稀疏表示α均最小，即

(10)

高分辨率字典Dh计算公式如

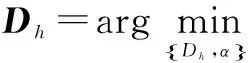
(11)

低分辨率字典Dl计算公式如

(12)

字典训练过程流程图如图2所示。

4改进的稀疏表示复原算法

对原始稀疏表示超分辨率复原算法的改进主要集中在两个方面：特征提取的改进、初始估计的改进。

4.1特征提取方法的改进

图像边缘是图像的重要特征，边缘特征提取是图像复原关键的一部分。前面提到特征提取F就是本文算法提取的图像边缘特征，是为了使训练出来的字典适用于大多数和训练数据相关的低分辨率复原图像，这样可以使得到的复原高分辨率图像分辨率更高。

算法中利用MATLAB函数库中conv2(二维卷积运算函数)进行图像的粗边缘提取，利用的是一阶、二阶梯度滤波算法。一阶梯度滤波算子如图3a、3b所示，二阶梯度滤波算子如图3c、3d所示。

改进算法中对二阶梯度滤波算法的算子进行改进，如图4a、4b所示。

以图5为例，分别进行原始二阶梯度滤波的图像特征提取和改进后二阶梯度滤波的图像特征提取处理，结果如图6所示，改进后的特征提取算法提取的特征更细腻，保留了更多的高频细节。后文将讲述这样改进将使图像的复原效果进一步提高。

4.2复原算法初始估计的改进

原始算法对于输入低分辨率图像先进行双三次插值放大，得到高分辨率的初始估计，双三次插值虽然效率很高，但是插值效果却有待提高，为了提高复原效果，将用边缘方向插值代替双三次插值，改进算法的处理效果较之前明显改善。

边缘方向插值的基本思想为：利用高分辨率图像和低分辨率图像协方差的几何对偶性质，用可以计算

的低分辨率图像的局部协方差系数对高分辨率图像进行自适应插值。

算法原理如下：

输入低分辨率图像Xi,j(尺寸是H×W)，用式(13)进行图像插值

Y2i,2j=Xi,j

(13)

(14)

Y2i+1,2j+1是插值得到的高分辨率图像，α是线性插值系数，它的计算公式如

α=R-1r

(15)

式中：R=[Rkl],(0≤k,l≤3) r=[rk],(0≤k≤3)是高分辨率图像的局部协方差系数，利用高分辨率图像和低分辨率图像协方差的几何对偶性可以由低分辨率图像的协方差计算出高分辨率图像的协方差，几何对偶性是指高分辨率图像和低分辨率图像沿相同方向的协方差是一致的，如图7所示。

图7中可以看到，当从Y2i,2j插值到Y2i+1,2j+1时的高分辨率协方差Rkl,rk和低分辨率协方差Rkl,rk是几何对偶的，几何对偶能促使不用明确估计边缘方向的情况下就能够计算二维信号的局部协方差。

用经典计算协方差的方法很容易计算出低分辨率图像的协方差如下

(16)

y=[y1,…,yk,…,yM2]T是低分辨率图像中M×M像素大小的一个数据变量，C是yk的沿对角线方向的4个相邻像素点，所以根据上面两个公式再根据高低分辨率协方差的一致性可以得到系数α为

α=(CTC)-1(CTy)

(17)

所以可以利用公式(14)进行边缘方向插值，改进复原效果。

5仿真结果

对于输入的彩色图像，根据人眼的视觉特性对亮度信息比较敏感，将彩色图像进行颜色空间的分离，分解成y、cb和cr三个分量，对y分量进行改进的稀疏表示的图像复原处理，对cb和cr分量只进行双三次插值处理。图像的评价是通过计算y分量的峰值信噪比(Peak Signal to Noise Ratio，PSNR)来完成，PSNR值越高，重建的效果越好。

5.1图像复原

对于如图8a所示的大小为256×256的高分辨率图像，对其进行下采样2倍得到128×128的低分辨率图像作为输入低分辨率图像，如图8b所示，算法处理过程中的图像块尺寸是5×5大小的像素，块与块之间的重叠像素是4，字典大小为512，稀疏正则化参数λ是0.15，稀疏正则化参数的取值依赖于输入图像的噪声水平，本次仿真输入的图像是低噪声图像，所以取λ=0.15，采样的图像块的个数取值为110 000。如图8所示为文献[6]稀疏表示原始算法和改进稀疏表示复原算法的复原效果比较图。

从图8可以看出，改进算法重建效果明显优于插值算法的结果，双三次插值结果过于模糊且缺乏高频信息。通过对重建图像的PSNR值比较可以知道改进算法得到的图像的PSNR值较高，说明改进算法有效。

对于Lena输入图像，分别采用双三次插值、稀疏表示算法和改进的稀疏表示复原算法进行处理，目标放大倍数设置为2倍，如图9所示，可见改进算法在视觉效果上较双三次插值有明显提高，不仅保留大部分图像细节，而且复原出的图像更接近于原始图像，比较PSNR值后发现也较稀疏表示原始算法有所提高。

5.2图像特征提取对复原效果的影响

图像复原中的字典学习不是对训练图像直接训练，而是针对图像的特征向量，因为直接对训练样本的特征进行学习，能够更好地抓住图像的高频分量之间的联系，进而准确地预测出高分辨率图像的高频信息，所以图像特征提取算法的选取直接影响重建的效果。

图像特征提取比较典型的方法包括：一阶、二阶梯度滤波算法、拉普拉斯滤波算法、索贝尔算法、普利维特算法和罗伯茨算法等，原始图像稀疏复原算法中的特征提取采用一阶、二阶梯度滤波算法，以低分辨率Lena图像作为输入图像，目标放大倍数为2倍，将以上特征提取算法分别用于稀疏表示的改进算法中，可以得到表1所示的PSNR值。

表1图像特征提取算法对复原效果的影响

从表1的PSNR值可以看到，改进一阶、二阶梯度滤波算法作为低分辨率图像的图像特征提取算法得到更高的PSNR值，说明改进的特征提取方法的有效性。

5.3目标放大倍数对复原效果的影响

对于图像超分辨率复原，还比较关心不同目标的放大倍数进行复原的问题，如图10所示为改进稀疏表示算法对于Lena低分辨率图像分别在放大倍数为2和4时的复原结果。

从图10可以看出，随着放大倍数的增加，复原效果却在减弱。通过比较表2的不同算法在不同放大倍数下的PSNR值可以看到随着放大倍数的增加，复原效果明显变差。

表2不同目标放大倍数对复原效果的影响

6结论

虽然稀疏表示的图像超分辨率复原算法较传统的基于重建的超分辨率复原算法取得更好的效果，但由于其复杂度较高，学习过程效率明显偏低，所以在工程上的应用并不多，如何提高学习过程的效率是接下来要注重研究的问题。

本文改进算法首先对图像特征提取过程进行改进，通过不断探索，找到了一条改进策略，提高了图像复原的效果，同时，算法在初始估计上也进行了改进，对于输入的低分辨率图像，通过边缘方向插值代替原始的双三次插值，实现图像的初始放大。

算法中同时用到了迭代反投影算法对重建的图像进行全局约束，而这种算法有一个很大的缺点：对高分辨率图像的错误校正具有局限性，接下来的工作也将继续寻找最优的全局约束算法，改善复原效果。

参考文献：

[1]肖杰雄．基于POCS算法的超分辨率图像重建[D]．上海：上海交通大学，2009．

[2]赵环旭，滕青芳．小波融合技术在运动模糊图像复原中的应用[J]．电视技术，2014，38(5)：9-11．

[3]FREEMANWT，LIUC．Advancesinmarkovrandomfieldsforvisionandimageprocessing[M].Boston，USA：MITPress，2011．

[4]MALLATS，YUG．Super-resolutionwithsparsemixingestimators[J]．IEEEtransactionsonimageprocessing，2010，19(11)：2889-2900．

[5]DONGWS，ZHANGL，RASTISLAVL，etal.Sparserepresentationbasedimageinterpolationwithnonlocalautoregressivemodeling[J]．IEEEtransactionsonimageprocessing，2013，22(4)：1382-1394．

[6]YANGJC，WRIGHTJ，THOMASS，etal.Imagesuper-resolutionviasparserepresentation[J]．IEEEtransactionsonimageprocessing，2010，19(11)：2861-2873．

[7]吴炜，陶青川．基于学习的图像增强技术[M]．西安：西安电子科技大学出版社，2013：141-143．

Improved image super-resolution via sparse representation

QIU Dawei，LIU Yanlong

(CollegeofInformationEngineering，TaiYuanUniversityofTechnology，Taiyuan030024，China)

Key words:sparse representation; feature extraction; edge interpolation

Abstract:In view of the feature on signal sparse decomposition, together with the characteristic of the image super-resolution, an algorithm of image super-resolution via sparse representation is designed in this paper. The training process of the two over-complete dictionary and the processing procedure of the resolution via sparse representation is described. And then, the improved algorithm of the optimizing the feature extraction algorithm and optimizing the initial value of low-resolution image with adaptively selects the directional edge direction interpolation are described in detail. Meanwhile, the simulation and verification are also given based on MATLAB. Experimental results show that improved algorithm can effectively extract more superior quality than original algorithm, image can be directly restored. At the same time, the improved algorithm can obtain better robustness.

中图分类号:TN957.52

文献标志码:B

DOI：10.16280/j.videoe.2016.01.027

基金项目：山西省自然科学基金项目(2013011017-3)

作者简介：

邱大伟(1991— )，硕士生，主要研究方向为图像处理、模式识别；

刘彦隆(1965— )，硕士生导师，主要研究方向为图像编码、图像处理、语音识别，为本文通讯作者。

责任编辑：许盈

收稿日期：2015-06-13

文献引用格式：邱大伟，刘彦隆.改进的稀疏表示图像超分辨率复原算法[J].电视技术,2016，40(1)135-140.

QIU D W，LIU Y L. Improved image super-resolution via sparse representation[J].Video engineering,2016,40(1)：135-140.