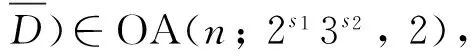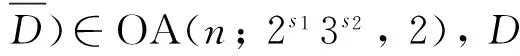混水平饱和正交设计在广义离散偏差下的均匀性

李洪毅，欧祖军，黎奇升

(1. 吉首大学师范学院，湖南 吉首　416000；2. 吉首大学数学与统计学院，湖南 吉首　416000)

混水平饱和正交设计在广义离散偏差下的均匀性

李洪毅1, 2，欧祖军2，黎奇升2

(1. 吉首大学师范学院，湖南 吉首416000；2. 吉首大学数学与统计学院，湖南 吉首416000)

摘要：针对二、 三混水平饱和正交设计d，在适当的划分下d=(D ⋮ ), 给出设计d的广义离散偏差与子设计)的广义字长型及均匀性模式的解析关系. 同时, 给出这类因子设计的广义离散偏差的下界. 最后, 通过例子来验证其结论.

关键词：混水平饱和正交设计; 广义离散偏差; 广义字长型; 均匀性模式

0引言

1基本概念

关于强度为2的二、 三混水平饱和正交设计, Qin[3]给出了下列结论.

(1)

对于任意的设计d∈u(n; 2s13S2)，其广义离散偏差值记为DDd((a1,b1), (a2,b2)), Chatterjee等[2]给出了如下关于[DDd((a1,b1), (a2,b2))]2的表达式：

(2)

其中:a1,b1,a2,b2为常数, 且a1>b1>0,a2>b2>0. 当a1=a2,b1=b2, DDd((a1,b1), (a2,b2))简记为DDd(a1,b1)，即为设计d的离散偏差，关于式(2)的详述参见文[2].

对于n次试验s个因子的设计d, 定义:

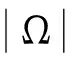
(3)

Ma和Fang[4]基于向量(A1(d), …,AS(d))给出了如下的最小广义低阶混杂(MGA)准则.

定义2对两个设计d1(n;qs)和d2(n;qs), 设r为使得Ar(d1)≠Ar(d2)的最小整数，如果Ar(d1)

现在来简单地描述最小投影均匀性(MPU)准则. 基于中心化L2-偏差，Fang和Qin[5]对于设计d∈u(n; 2s)，利用Ii(d)来衡量设计d的i维投影均匀性，其中:

向量(I1(d), …,IS(d))被称为设计d的均匀性模式[5-6].

引理2设d∈u(n; 2s), 对任意的j(1≤j≤s),Aj(d)和Ij(d)有如下的线性关系：

(4)

定义3对两个设计d1∈u(n; 2s)和d2∈u(n; 2s), 设r为使得Ir(d1)≠Ir(d2)的最小整数，如果Ir(d1)

对于二水平设计的投影均匀性模式的下界,Zhang和Qin[6]给出了下面的结论：

引理3设d∈u(n; 2s), 则:

(5)

其中:Rn, l为n除以2l的余数，1≤l≤s.

2主要结论

(6a)

(6b)

(6c)

证明只给出式(6a)的证明, 其余等式可类似证明. 由式(1)和(2)，可得:

(7a)

(7b)

其中：

证明只考虑式(7a)的证明, 其余等式可类似证明. 据式(4)和式(6a)可得：

根据Zhang和Qin[6]给出二水平设计的投影均匀性模式的下界, 有下面的定理.

(8a)

(8b)

其中:

Rn, l为n除以2l的余数，1≤l≤s1.

证明只考虑式(8a)的证明, 其余的可类似证明，由式(5)和式(7a)即可得式(8a).

表1　d的设计表及数值结果

参考文献：

[1]HICKERNELLFJ,LIUMQ.Uniformdesignslimitaliasing[J].Biometrika, 2002, 89: 893-904.

[2]CHATTERJEEK,QINH.Generalizeddiscretediscrepancyanditsapplicationsinexperimentaldesigns[J].JournalofStatisticalPlanningandInference, 2011, 141: 951-960.

[3]QINH.Characterizationofgeneralizedaberrationofsomedesignsintermsoftheircomplementarydesign[J].JournalofStatisticalPlanningandInference, 2003, 117: 141-151.

[4]MACX,FANGKT.Anoteongeneralizedaberrationfactorialdesigns[J].Metrika, 2001, 53: 85-93.

[5]FANGKT,QINH.Uniformitypatternandrelatedcriteriafortwo-levelfactorials[J].ScienceinChina：SerA, 2005, 48: 1-11.

[6]ZHANGSL,QINH.Minimumprojectionuniformitycriterionanditsapplication[J].Statistics&ProbabilityLetters, 2006, 76: 634-640.

[7] 李洪毅, 欧祖军. 互补设计在Lee偏差下的均匀性[J]. 华中师范大学学报(自然科学版), 2011, 45(1): 1-5.

(责任编辑： 沈芸)

Uniformity in mixed levels saturated orthogonal designs in term of generalized discrete discrepancy

LI Hongyi1, 2, OU Zujun2, LI Qisheng2

(1. Normal College, Jishou University, Jishou, Hunan 416000，China;2. College of Mathematics and Statistics, Jishou University, Jishou, Hunan 416000，China)

Abstract:We consider a kind of mixed two and three levels saturated orthogonal designs d. Under a proper decomposition of d=(D ⋮ ), we give connections between the generalized discrete discrepancy of d and generalized word length pattern or uniformity pattern of D or . Meanwhile, we also present the lower bound of generalized discrete discrepancy of this kind of fractional factorials. Finally, an illustrative example is given to shown our theoretical results.

Keywords:mixed levels saturated orthogonal design; generalized discrete discrepancy; generalized word length pattern; uniformity pattern

DOI:10.7631/issn.1000-2243.2016.03.0368

文章编号：1000-2243(2016)03-0368-07

收稿日期:2014-08-27

通讯作者:欧祖军(1979-)，副教授，主要从事试验设计及计算机试验研究, ozj9325@mail.ccnu.edu.cn

基金项目：国家自然科学基金资助项目(11201177, 11561025); 湖南省教育厅优秀青年基金资助项目(14B146)

中图分类号：O212.6

文献标识码：A