一种二维实空间上构造框架的算法及其实现

王 维，朱玉灿

(福州大学数学与计算机科学学院，福建 福州　350116)

一种二维实空间上构造框架的算法及其实现

王 维，朱玉灿

(福州大学数学与计算机科学学院，福建 福州350116)

摘要：针对二维实空间上具体框架的构造方法问题，提出一种二维实空间上构造具体框架和紧框架的算法. 通过编程实现该算法，得到了在满足一定条件下，利用该算法可以构造不同需求下的二维实空间的具体框架和紧框架的结论.

关键词：框架； 二维实空间； 算法

0引言

Hilbert空间的框架是标准正交基的一种推广，在有限维Hilbert空间中，框架是一个可张成该空间的冗余集. 框架的一些性质在图像处理、 编码和传输、 无线电通讯等领域得到了广泛的应用. 如，由于框架的冗余性，使得框架能够很好地恢复丢失的数据； 在信号处理方面，框架的范数可以代表着物理能量值. 在具体的应用中，时常需要构造满足具体问题中的特殊要求的框架. 因此，如何在Hilbert空间中构造框架成为了一个热点. 文献研究了在给定框架算子或者框架算子的谱和模长等条件下相关框架的存在性，并没有给出具体的算法.

下面介绍框架的相关概念以及几个命题，它们是该算法设计的理论依据.

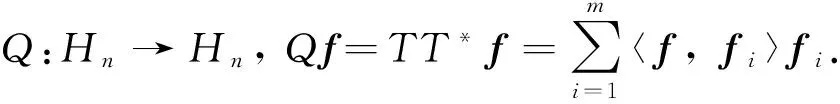
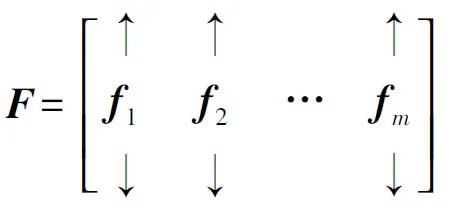
如果Λ为对角矩阵且diag(Λ)=(λ1,λ2, …,λm)，则存在m阶正交矩阵O，使得

1算法分析

1.1算法思想

在R2中，框架算子所对应的矩阵S是一个二阶的正定的实对称矩阵，因而存在二阶正交矩阵O和对角矩阵Λ使S=OΛO*成立，其中diag(Λ)=(λ1,λ2)，λ1,λ2分别为S的两个特征值(设λ1≥λ2>0). 令m×2阶矩阵Δ为：

那么ΔΔ*为m阶对角矩阵，其中diag(ΔΔ*)=(λ1,λ2, 0, …, 0). 由命题2知，当满足条件：

(1)

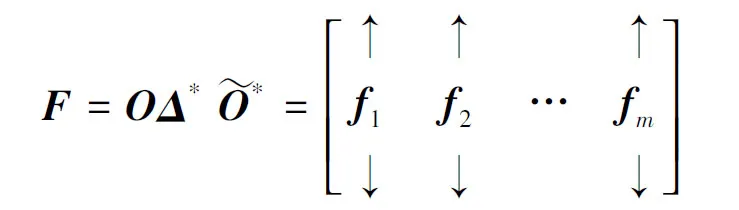
1.2正交矩阵O的构造

对于两个固定的正实数λ1、 λ2，对应着无穷多个以它们为特征值的二阶的实对称矩阵S. 这也说明对R2中每个具有相同框架上界与框架下界的框架，可以对应着不同的框架算子Q. 而在正实数λ1、λ2固定的情况下，改变框架算子Q只能由正交矩阵O决定. 以下面方式构造正交矩阵O：

(2)

此时，根据控制参数z(z∈[0, 2π])可以得到各种不同的正交矩阵O. 其中，当z取遍闭区间[0, 2π]内的值时，就构造出了全部的正交矩阵O. 也即在正实数λ1、λ2固定的情况下，通过z可以控制生成不同的框架算子Q，并且它们都有着公共的特征值λ1、λ2. 特别地，当需求为生成紧框架时，则需要令z=0，即O=I2，其中I2为二阶单位矩阵.

1.3确定需求框架的最佳框架上界λmax与最佳框架下界λmin

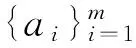
(3)

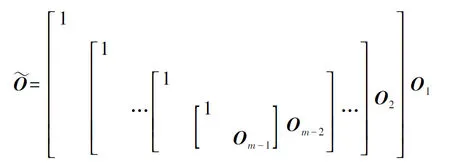
(4)

构造如下形式的l阶正交矩阵Oj：

(5)

其中： *=(Aj(k,k)-Aj(1, 1))sintcost. 此时Aj+1是l-1阶对角矩阵，且Aj+1只有两种可能：

或者

2算法设计及实现的伪代码

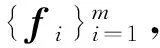
伪代码：

程序开始

Step1： If 不满足式(1) Then输出(“参数有误，请重新输入正确参数”)程序结束

End if

Step2： IfI=0 Then 以式(2)的方式构造O

λmax←λ1

λmin←λ2

Else ifI=1 Then

If不满足式(3) Then 输出(“不存在紧框架，请重新输入正确参数”)程序结束

End if

O←I2

λmin←λmax

End if

Step3～6： 依式(4)构造A1

Forj=1 tom-1

Begin

l←m-j+1

Fori=2 tol

Begin

Break

End if

End

根据k值，依式(5)构造Oj

End if

End

Step7： Ifm>2 Then

Forw=1 tom-2

Begin

Om-1-w←Bw+2Om-1-w

End

End if

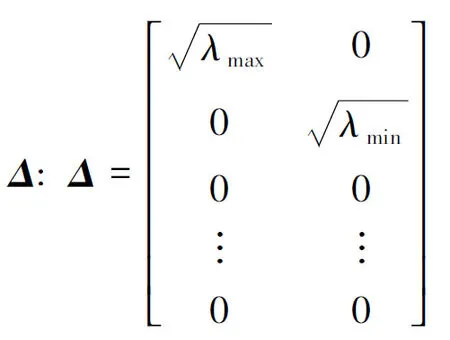
输出： F

程序结束

需要说明的是： 在输入参数λ1、λ2固定的情况下，正交矩阵O的控制参数z提供了可选取不同Q作为最终输出框架的框架算子的机会，当z取遍整个闭区间[0, 2π]的值时，通过该算法可以计算出全部以{λ1,λ2}为特征值的框架算子Q的框架.

3算例以及验证分析

根据上面算法设计的思路，经过计算编程实现，下面给出算例和验证分析.

表1　参数I，z取不同值时输出的结果

另外，从表2可以看出，在其他输入参数不变的情况下，当正交矩阵O的控制参数z取不同值时，意味着可选择特征值一样却又完全不同的Q作为最终输出框架的框架算子，这也验证了该算法的灵活性.

下面将尝试把该框架构造的算法推广到三维以及多维空间上，使其能更广泛地应用在高维信号的处理中.其实现也将更为复杂，需要考虑更多的问题，比如多维正交矩阵的选取将更加多样化等，还要考虑一些数据结构的处理问题.

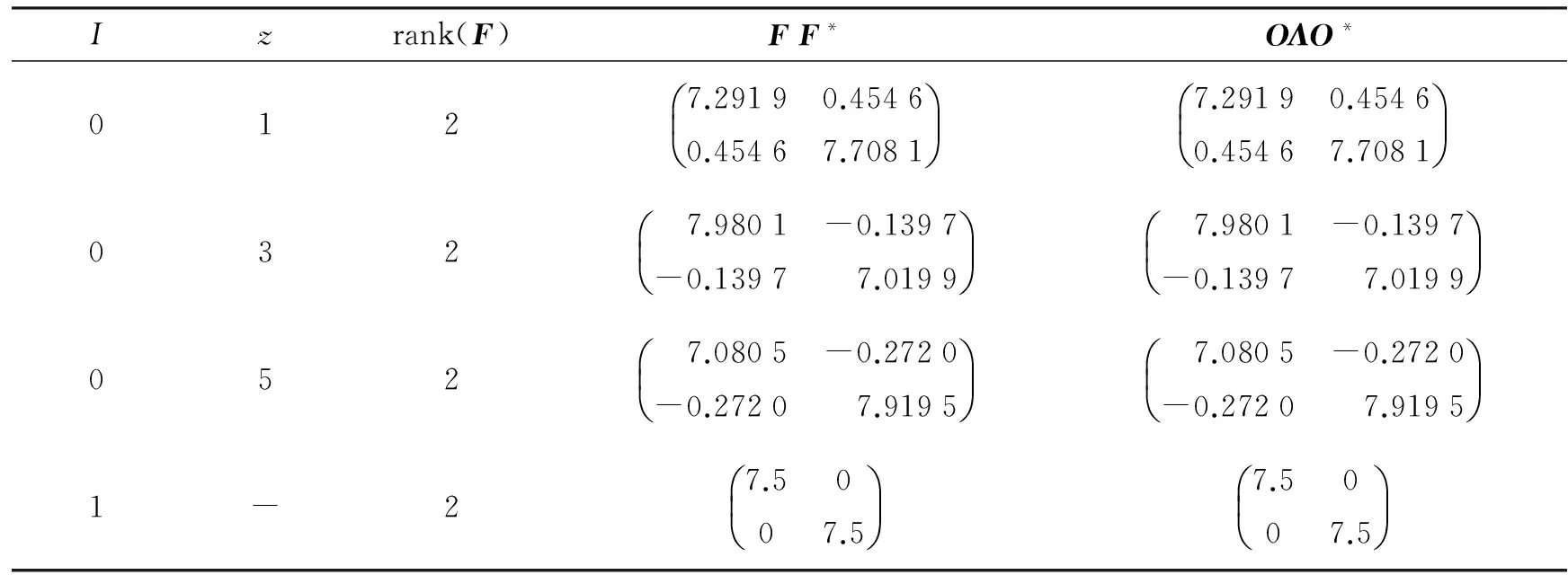
表2　参数I，z取不同值时输出的矩阵F的秩、 FF*以及OΛO*

表3　参数I，z取不同值时输出结果的模长

参考文献：

[1] CHAN R H, RIEMENSCHNEIDER S D, SHEN L,etal. Tight frame: an efficient way for high-resolution image reconstruction[J]. Appl Comput Harmon Anal, 2004, 17: 91-115.

[2] STROHMER T, HEATH J R. Grassmanian frames with applications to coding and communications[J]. Appl Comput Harmon Anal, 2003, 14: 257-275.

[3] HEATH R W, PAUKAJ A J. Linear dispersion codes for MIMO systems based on frame theory[J]. IEEE Trans Signal Process, 2002, 50: 2 429-2 441.

[4] CASAZZA P G, LEON M T. Existence and construction of finite frames with a given frame operator[J]. International Journal of Pure and Applied Mathematics，2010, 63: 149-158.

[5] CAHILL J，FICKUS M, MIXON D G，etal. Constructing finite frames of a given spectrum and set of lengths[J]. Applied and Computational Harmonic Analysis, 2013, 35(1): 52-73.

[6] ROLLI W J. Constructing frames for finite dimensional Hilbert spaces[J]. Journal of Mathematical Analysis and Applications, 2006, 321(1): 388-395.

[7] CASAZZA P G. Finite frames: theory and applications[M]. Boston: Birkhauser, 2012.

(责任编辑： 林晓)

An algorithm for constructing frames and its implementation on a two-dimensional real space

WANG Wei, ZHU Yucan

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China)

Abstract:This paper focuses on the construction of frames on a two-dimensional real space. We present an algorithm for constructing frames and tight frames on a two-dimensional real space and give the Pseudo-code of that algorithm. We get the conclusion that we can construct the specific frames on a two-dimensional real space for different needs by the algorithm.

Keywords:frame; two-dimensional real space; algorithm

DOI:10.7631/issn.1000-2243.2016.03.0348

文章编号：1000-2243(2016)03-0348-07

收稿日期:2014-03-26

通讯作者:朱玉灿(1963-)，教授，主要从事框架理论、 几何函数论、 多复变函数几何理论研究，zhuyucan@fzu.edu.cn

基金项目：福建省自然科学基金资助项目(2012J01005)

中图分类号：O177.1

文献标识码：A