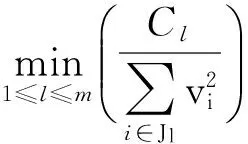有限维Hilbert空间中框架和fusion框架的最大鲁棒度

潘 倩，舒志彪

(福州大学数学与计算机科学学院，福建 福州　350116)

有限维Hilbert空间中框架和fusion框架的最大鲁棒度

潘 倩，舒志彪

(福州大学数学与计算机科学学院，福建 福州350116)

摘要：根据框架的最大鲁棒度的定义，给出框架的最大鲁棒度的性质，并讨论经过一些矩阵扰动后框架最大鲁棒度的变化. 对fusion框架的最大鲁棒度的上界进行估计，得到经过一些特殊扰动后fusion框架的最大鲁棒度的变化.

关键词：框架; fusion框架; Hilbert空间; 最大鲁棒度; 扰动

1引言

在过去30年，框架系统因为其鲁棒性、 稳定性以及不唯一的向量表示，使得它被广泛应用于滤波器组理论[1]、 信号和图像处理[2]等领域. 框架具有冗余性，这样的冗余产生了鲁棒性，这使得框架对传输的错误表现出较低的敏感性. 在更广泛的向量上传播信息时，丢失的信息可以得到还原，还可以减轻信号中噪声的影响，所以对于框架的擦除鲁棒性研究[3-4]显得尤为重要. 由于框架在实际问题中的应用大部分都表现在有限维向量空间中，因此国内外有许多学者对有限维框架进行一些深入、 系统的研究[5-6]. 然而，传统的单一框架系统很难在大量新的应用设置中建立模型. 于是在本文中研究fusion框架的最大鲁棒度[7-8]. 关于fusion框架的擦除鲁棒性研究已经得到了一些结论[9-10], 在文献[11]中, 提出有限维Hilbert空间中框架最大鲁棒度的概念.

本文采用如下记号: Hn表示n维Hilbert空间，l、 m、 r、 k、 n为正整数，N为正整数集，I是N的子集，Rn为n维实向量空间. 矩阵G的秩记为rank(G)，πW:Hn→W表示从Hn到W的正交投影.

首先简要介绍框架和fusion框架的一些基本概念和性质.

成立. A ，B分别称为框架的下界和上界.

则称{(Wi，vi)}i∈I是Hn的fusion框架，C，D分别称为fusion框架的下界和上界.

如果一个矩阵F的所有行向量是Hn中的一个框架，默认该框架的最大鲁棒度用rob(F)表示.

2有限维Hilbert空间中框架的最大鲁棒度

rob(F1∪F2)≥rob(F1)+rob(F2)+1

证明假设rob(F1)=a，rob(F2)=b，其中a和b都是正整数. 假设Φ=(F1)∪(F2). 当Φ中任意去掉a+b+1个向量时，那么这a+b+1个向量一部分属于F1，另一部分属于F2. 设其中属于F1中的向量个数为k1，属于F2中的向量个数为k2，则k1+k2=a+b+1. 下面分两种情况讨论.

1) 当k1≤a时，k1≤rob(F1)，根据擦除鲁棒性以及最大鲁棒度的定义，任意去掉F1中的k1个向量，则剩下的向量仍是框架. 再并上擦掉F2中k2个向量后剩下的向量，则仍然还是框架.

2)当k1>a，则k2

综述所述，任意去掉Φ中a+b+1个向量，剩下的向量仍然是框架. 根据最大鲁棒度的定义，

rob(Φ)=rob(F1∪F2)≥rob(F1)+rob(F2)+1

下面讨论框架的r擦除鲁棒性经过一些特殊的矩阵扰动后的变化.

证明

Φ任意去掉l行所得的矩阵Φ1=A1F1D，其中F1为F去掉l行后的矩阵，A1为A去掉对应l行和l列后的矩阵. 因为D是行满秩矩阵，所以有D=[En0]Q，其中En为n阶单位矩阵，Q为可逆矩阵. 所以F1D=F1[En0]Q=[F1En0]Q，又因为A1为可逆矩阵，那么

rank(A1F1D)=rank(A1[F1En0]Q)=rank(F1En)=rank(F1)

也就是说矩阵Φ的行向量组成的框架和F一样都具有r擦除鲁棒性.

注1上述定理中当矩阵A中互换任意行后，结论也是成立的.

对于定理2，当A为任意可逆矩阵时不一定成立. 因为F的行向量互换两行或者对某一行乘上一个非零的数都不会改变其行向量组成框架的擦除鲁棒性. 但如果把某一行的k倍加到另外一行，则擦除鲁棒性会发生变化. 下面通过一个例子说明定理2中A为任意可逆矩阵时结论不成立.

从定理2和推论1可以发现，右乘一个行满秩矩阵不改变框架的最大鲁棒度. 下面给出左乘一个特殊的列满秩矩阵后，关于框架最大鲁棒度的一个不等式.

证明设rob(F )=r，若矩阵A去掉可逆对角子矩阵所在行以后剩下的l-k行全为0，则根据定理2及注1知等号成立; 若剩下的l-k行不全为0，其实Φ是一个l×n的矩阵. 因为A中存在某k行组成的子矩阵是通过一k×k可逆对角矩阵互换某些行得到的，说明矩阵Φ的行向量对应的框架中存在一组a1f1，a2f2，…，akfk的向量，其它向量则可由它们线性表出，其中a1，a2，…，ak为非零实数. 所以rob(Φ)至少为r，即rob(Φ)≥rob(F).

矩阵的秩通过左乘列满秩矩阵或者右乘行满秩矩阵不改变矩阵本身的秩. 但是对于空间的框架，其元素作为行向量组成的矩阵在进行左乘列满秩矩阵后，所得的矩阵的行向量仍然是空间的框架. 但其最大鲁棒度却发生了改变. 也就是说通过左乘列满秩矩阵作用后，虽然框架本身秩不变，但不能保证框架跟原来一样在擦除一部分向量后仍可以张成整个空间.

3有限维Hilbert空间中fusion框架的最大鲁棒度

根据框架的最大鲁棒度的定义，给出fusion框架的最大鲁棒度的定义.

给出rob(W)的一个上界估计.

S={I⊆{1，2，…，k}:span({Wi}i∈I)=Hn}

注3引理2为文献[8]中的命题5.2在有限维空间中的表达，易看出当ε=0时，结论成立.

在引理2中ε取零的情况下，得出定理5中的等式. 当ε不为零时，仍存在一种特殊情况.

参考文献：

[1] BOLCSKEI H，HLAWATSCH F，FEICHTINGER H G. Frame-theoretic analysis of oversampled filter banks[J]. IEEE Transactions on Signal Processing，1998，46(12): 3 256-3 268.

[2] CANDèS E J，DONOHO D L. New tight frames of curvelets and optimal representations of objects with piecewise C2 singularities [J]. Communications on Pure and Applied Mathematics，2003，57(2): 219-266.

[3] FICKUS M，MIXON D G. Numerically erasure-robust frames[J]. Linear Algebra and Its Applications，2012，437(6): 1 394-1 407.

[4] ALEXEEV B，CAHILL J，MIXON D G. Full spark frames[J]. Journal of Fourier Analysis and Applications，2012，18(6): 1 167-1 194.

[5] CASAZZA P G，KUTYNIOK G. Finite frames: theory and applications[M]. Boston: Birkhǎuser，2012.

[6] CHRISTENSEN O. An introduction to frames and Riesz bases[M]. Boston: Birkhǎuser，2003.

[7] CASAZZA P G，KUTYNIOK G. Frames of subspaces[J]. Wavelets，Frames and Operator Theory，2004: 87-113.

[8] CASAZZA P G，KUTYNIOK G，LI S. Fusion frames and distributed processing[J]. Applied and Computational Harmonic Analysis，2008，25(1): 114-132.

[9] KUTYNIOK G，PEZESHKI A，CALDERBANK R，etal. Robust dimension reduction，fusion frames，and Grassmannian packings[J]. Applied and Computational Harmonic Analysis，2009，26(1): 64-76.

[10] CASAZZA P G，KUTYNIOK G. Robustness of fusion frames under erasures of subspaces and of local frame vectors[J]. Contemporary Mathematics，2008，464: 149-160.

[11] COPENHAVER M S，KIM Y H，LOGAN C，etal. Maximum robustness and surgery of frames in finite dimensions[J].Linear Algebra and Its Applications，2013，439(5): 1 330-1 339.

(责任编辑： 蒋培玉)

Maximum robustness of frames and fusion frames in finite dimensional Hilbert spaces

PAN Qian，SHU Zhibiao

(College of Mathematics and Computer Science，Fuzhou University，Fuzhou，Fujian 350116，China)

Abstract:Based on the definition of the maximum robustness of frames，we give some characterizations about the maximum robustness of frames，and discuss the change of maximum robustness of frames under some matrix perturbation. We also estimate the upper bound of the maximum robustness of fusion frames，and discuss the change of maximum robustness of fusion frames under some special perturbation.

Keywords:frame; fusion frame; Hilbert spaces; maximum robustness; perturbation

DOI:10.7631/issn.1000-2243.2016.03.0337

文章编号：1000-2243(2016)03-0337-05

收稿日期:2014-07-03

通讯作者:舒志彪(1958-), 副教授, 主要从事小波分析、 图像处理、 信息隐藏等方面的研究，szb@fzu.edu.cn

基金项目:福建省自然科学基金资助项目(2012J01005, 2014J01007); 福州大学科技发展基金资助项目 (2012-XQ-29)

中图分类号：O177.1

文献标识码：A