极大单调算子零点的强收敛定理
叶静妮
(福州大学至诚学院,福建 福州 350002)
极大单调算子零点的强收敛定理
叶静妮
(福州大学至诚学院,福建 福州350002)
摘要:利用广义投影算子技巧,在一致光滑、 一致凸的Banach空间中,建立一种关于极大单调算子零点的具有误差项的投影算法,并在适当的条件下,证明了该算法的强收敛性. 所得结果在关于极大单调算子的零点计算中有新颖性,改进了众多熟知的结果.
关键词:极大单调算子; 零点; 强收敛; 误差项
0引言
构造迭代算法去逼近极大单调算子的零点是非线性分析的一个热点问题, 许多纯数学问题和应用数学问题都可纳入极大单调算子的零点框架中加以研究. 因此,它在理论上和实际应用领域都具有重要的意义. 近年来,许多学者引入了各种不同的迭代算法来寻求极大单调算子的零点.
2006年,Yanes 等[1]为提高算法的收敛速度,在Hilbert空间中构造如下具有误差项的投影算法:
(1)
(2)
产生的序列{xn}强收敛于极大单调算子T的零点∏T-10x0.
受文[1-2]的启发,借助于广义投影技巧,本研究在Banach 空间中,构造了一种新的具有误差项的投影算法,并在合适的条件下,证明了算法强收敛于算子零点. 本研究是文[1-3]工作的进一步深入和延续,在一定程度上改进了文献[1-3]的结果.
1预备知识

多值映像T:D(T)⊂E→2E*称为单调的,如果〈x1-x2,y1-y2〉≥0,∀xi∈D(T),yi∈Txi,i=1,2. T称为极大单调算子,如果R(J+rT)=E*,∀r>0. 对单调算子T,用T-10表示T的零点集,即T-10={x∈D(T):0∈Tx}. 下面追述与本研究有关的概念和有用的结论.
引理1[4-5]正规对偶映射J具有如下性质:
1) 如果E是实的自反、 光滑的Banach空间,那么J:E→2E*是单值的且JE=E*;
2) 如果E是实的一致光滑的Banach空间,那么J:E→2E*作用在E的有界子集上是一致连续的;
3) 如果E是实的光滑、 一致凸的Banach空间,那么J-1:E*→E也是对偶映射,且作用在E*的有界子集上是一致连续的.




定义2设E是实的自反、 光滑、 严格凸的Banach空间,C为E的非空闭凸子集,定义广义投影算子:

其中,

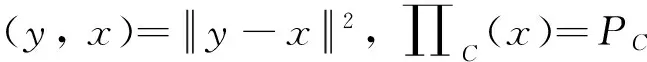
引理4[7]设E是实的自反、 光滑、 严格凸的Banach空间,C为E的非空闭凸子集. 对x∈E,有:


引理6[8]设E是实的自反、 光滑、 严格凸的Banach空间,T:E→2E*是极大单调算子,且T-10≠Φ,那么∀x∈E,y∈T-10,r>0,有:

引理7[7]设E是实的自反、 光滑、 严格凸的Banach空间,C为E的非空闭凸子集,设x∈E,z∈C,那么:
z=∏Cx⟺〈y-z,Jx-Jz〉≤0(∀y∈C)
2主要结论

(3)
如果以下条件满足:

2) {rn}⊂(0,+∞),infnrn>0;
则序列{xn}强收敛于∏Dx0.
证明分为6个步骤来完成定理的证明.
第1步证明Hn∩Wn是E的闭凸子集. 事实上,易看出Wn是E的闭凸子集.
所以,Hn是E的闭凸子集. 于是,Hn∩Wn是E的闭凸子集.
第2步证明D⊂Hn∩Wn.

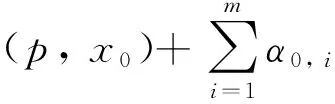
(4)
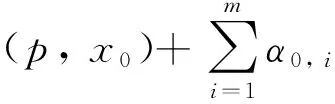


从而p∈Hn. 又由引理7有:
〈p-xn,Jx0-Jxn〉=〈p-∏Hn-1∩Wn-1x0,Jx0-J∏Hn-1∩Wn-1x0〉≤0
所以,p∈Wn. 于是p∈Hn∩Wn. 从而有: D⊂Hn∩Wn,∀n≥0.

∀p∈D⊂Hn∩Wn,因为xn=∏Wnx0,xn+1=∏Hn∩Wnx0⊂Wn,所以: φ(xn,x0)≤φ(xn+1,x0). 从而{φ(xn,x0)}单调递增. 又:


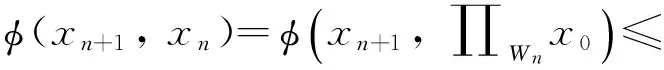
所以:
(5)
从而由引理5,有:
(6)
(7)
而:
(8)
(9)
所以由式(5)和(6),有:
(10)
再由引理5,有:
(11)
由式(6)得:
(12)
另外,∀p∈D,由引理3,有:

(13)


所以:

(14)
而:
由式(12)及引理1,有:
(15)
而:
由式(12)及引理1,得:
(16)
由式(14)~(16),有:
(17)


从而:
又因为infnrn>0,于是:

(18)
所以:
类似于定理1,容易得到如下的定理.
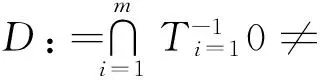
(19)

参考文献:
[1] YANES C M,XU H K. Strong convergence of the CQ method for fixed point iteration processes[J]. Nonlinear Anal,2006,64: 2 400-2 411.
[2] WEI Li,ZHOU Haiyun. Strong convergence of projection scheme for zeros of maximal monotone operators[J]. Nonlinear Anal,2009,71: 341-346.
[3] ALBER Y I. Metric and generalized projection operators in Banach spaces: properties and applications,theory and applications of nonlinear operators of accretive and monotone type[J]. Func Differ Equ,1993(1): 15-50.
[4] TAKAHASHI W. Nonlinear functional analysis[M].Yokohama: Yokohama Publishers,2000.
[5] PASCALI D,SBURLAN S. Nonlinear mapppings of monotone type[M]. Romania: Sijithoff and Noordhoff,1978.
[6] XU H K. Inequalities in Banach spaces with applications[J]. Nonlinear Anal,1991,16: 1 127-1 138.
[7] KAMIMURA S,TAKAHASHI W. Strong convergence of a proximal-type algorithm in a Banach space[J]. SIAM J Optim,2002,13: 938-945.
[8] KOHSAKA F,TAKAHASHI W. Strong convergence of an iterative sequence for maximal monotone operators in a Banach space[J]. Abstr Appl Anal,2004(3): 239-249.
(责任编辑: 沈芸)
Strong convergence for zeros of maximal monotone operators
YE Jingni
(Zhicheng College,Fuzhou University,Fuzhou,Fujian 350002,China)
Abstract:We introduce an iterative scheme by projection scheme for zeros of maximal monotone operators with errors in a real uniformly smooth and uniformly convex Banach space. Under suitable condition, some strong convergence theorems are proved. To some extent, it is meaningful to compute common zeros of maximal monotone operators. The results improve and extend some known corresponding results.
Keywords:maximal monotone operators; zeros; strong convergence; errors
DOI:10.7631/issn.1000-2243.2016.03.0331
文章编号:1000-2243(2016)03-0331-06
收稿日期:2013-12-16
通讯作者:叶静妮(1981-),硕士,副教授,主要从事非线性泛函分析研究,46793299@qq.com
基金项目:福建省中青年教师教育科研资助项目(JA13363,JA14365)
中图分类号:O177.91
文献标识码:A

