摆式-滚珠隔震器试验研究与数值模拟
田志昌,蔡杰峰,范雷彪,赵根田
1.内蒙古科技大学建筑与土木工程,内蒙古包头0140002.内蒙古包头市地震局,内蒙古包头014000
摆式-滚珠隔震器试验研究与数值模拟
田志昌1,蔡杰峰1,范雷彪2,赵根田1
1.内蒙古科技大学建筑与土木工程,内蒙古包头014000
2.内蒙古包头市地震局,内蒙古包头014000
摘要:本文对一种新型摆式-滚珠隔震器在水平低周往复荷载作用下的力学性能进行试验研究与数值模拟。试验结果表明,其滞回曲线规则饱满,具有较好的隔震效果和自动回复性能。ABAUES有限元软件建立实体模型,模拟结果与试验结果相吻合。通过盈建科有限元软件对实际工程案例建立三维框架模型对安装隔震支座结构与未安装隔震支座结构进行对比分析,结果显示出隔震支座具有显著的隔震效果。
关键词:新型摆式-滚珠隔震器;性能试验;数值模拟
地震灾害频繁的发生带来的不仅仅是大量人员的伤亡更多的是经济财产的损失。传统抗震结构通过本身耗能方式进行抵御地震,这极易导致结构的损伤以及倒塌。国内外的抗震理论和技术的发展,隔震技术成为较为有效的抗震手段之一。
最早研究以及得到实际应用的是摩擦滑移隔震装置,但因其不具备自我恢复性能、滑移性能不易把控,极易出现滑移失稳现象而导致滑移隔震发展缓慢。1985年在美国加州大学伯克利分校由Zayas等人对滑移隔震进行改良并成功的解决了平移滑动装置不能自我恢复的难题,并提出了摩擦摆隔震装置(FPB/FPS)[1-3]。摩擦摆隔震支座具备了平面滑移隔震装置对地震激励频率范围低敏性和高稳定性等特性外[4-6],还具有自我恢复性能,不需要增加阻尼向心结构,较好的隔震和消能机制等综合性能,经过30年的研究与发展,国内外许多专家学者对FPS进行了改进并做了深入研究[7-8],为FPS以后发展提供了大量的试验以及理论依据。
本文提出一种新型摆式-滚珠隔震装置,可避免由于传统的球面摩擦摆隔震支座(FPB)一旦曲率半径确定其隔震周期也随之确定,而在近断层常伴有长周期脉冲型地震波容易导致与上部结构产生低频共振现[9-12]。新型隔震器的力学性能研究通过对其进行试验研究和有限元模拟相互印证,结合实际工程案例,分析新型隔震器在多层钢筋混凝土框架中的耗能性能和隔震效果。

图1 摆式-滚珠隔震装置Fig.1 Tilting - Ball isolation device
1 新型隔震器的构造
新型隔震器如图1所示。该装置由上扣盖、滚珠、活动支盘、固定盆座四部分构成,(在固定盆座内放置24颗直径为60 mm滚珠)。新型隔震器能够将地震作用力(水平方向)任意方向进行有效隔离,自复位效果较好。新型隔震器的的滑动面与传统FPB滑动面构造不同,可避免地震出现共振。
2 新型隔震器的试验研究
本次试验为了更加准确的研究隔震器的力学性能[13]加工制作了直径为1 m的大直径的隔震器。材料均为高强度洛钢制成,隔震器由专业工作人员进行加工制造。为了隔震器能够完成加载试验和更加直观试验效果,将隔震装置进行倒置,将上扣盖浇筑在1800×1800×500 mm混凝土基础内,混凝土基础内设置双排双向HRB335 25#钢筋,浇筑C35混凝土。
试验采用150 KN MTS液压伺服作动器对隔震器固定盆座施加水平力,利用液压千斤顶以及反力梁提供竖向荷载,为保证隔震器的受水平力时上扣盖的稳定,将混凝土基础与地沟用高强度锚栓固定,同时将竖向千斤顶安装在滑动装置底部随着隔震器的整体移动。考虑到实际情况将固定盆座上增加5 cm厚度的钢板与水平千斤顶连接。千斤顶与反力墙、隔震器、反力钢梁均采用高强度螺栓连接。试验装置如图2,图3所示。

1.反力墙;2.反力平衡钢梁;3.滑移装置;4.液压千斤顶(500 KN);5.传感器;6.新型隔震器试件;7.固定锚栓;8.基础混凝土;9.MTS液压伺服作动器(150 KN)1. Anti-force wall;2. Anti-force balance steel beam;3. The slip device;4. The hydraulic jack(500 KN);5. The sensor;6. Neotype Isolator specimen;7. Anchor bolts;8. Concrete foundation;9. MTS hydraulic servo actuator(150 KN)
水平力加载以位移控制为加载制度,水平位移量分别是30、60、100 mm,根据不同的水平位移量分别采用0.1赫兹、0.3赫兹、0.5赫兹、1赫兹,等四种频率加载,竖向荷载分为30 kN,60 kN,100 KN等三种情况。
试验过程顺利。为避免繁琐,固此处以竖向荷载为60 KN为例,水平力加载频率为0.1赫兹时所得的滞回曲线,如图4所示。


3 新型隔震器的有限元分析
3.1ABAQUS模型建立
为了验证试验所得滞回曲线与新型隔震器的参数的正确性,结合试验结果,本文通过ABAQUS建立实体单元模拟新型隔震器的力学性能。各个构件的材料属性均按照实际钢材的材料属性建立本构关系;选取E=2.1×105MPa,v=0.3。由于新型减震器模型函数曲面复杂和摩擦系数大引起的网格不易划分及分析难收敛等问题,采用C3D4单元[14],经证明此单元比(C3D8R)可靠性与精度要高[15]。上扣盖的球面与活动支盘设有接触对,接触对的主面为活动支盘,从动面为球面划分更细,采用系统默认的“硬接触”;滚珠采用轴承钢GCr15由于钢珠与上扣盖和活动支盘同时接触,选择钢珠为主面,上扣件、活动支盘设置为从面,接触属性选择“面面接触”。假设接触面的切摩擦力遵循库伦定律,及摩擦系数是常数,且动摩擦与静摩擦一致[16]。加载制度同试验加载一致。摆式—滚珠隔震器的有限元实体模型如图5所示。
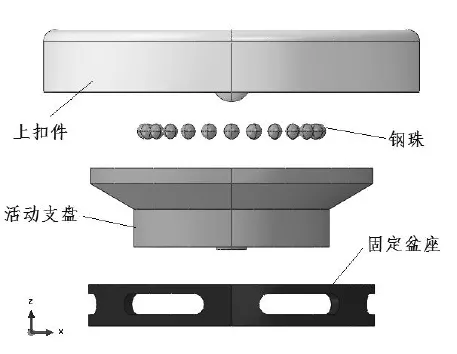
图5 新型隔震器的有限元模型Fig.5 Finite element model of the neotype Isolator

图6 新型隔震器的滞回曲线Fig.6 Hysteresis curve of the neotype Isolator
3.2结果分析
参照国家标准《球型支座技术条件》(GB/T 17955-2000)中的要求对于隔震器的摩擦系数进行测定,经过多次试验测得结果较为接近,表明摩擦系数基本上稳定。表2为摩擦系数。

表2 摩擦系数平均值Table 2 The averages of friction coefficients
图6所示为试验和数值模拟所得到的隔震器的滞回曲线对比,从图中可以得到,试验结果与模拟结果吻合。
新型隔震器的回复力测定:先施加竖向荷载,再由水平力将隔震器推到侧向设计位移,然后释放侧向约束,使得隔震器的竖向荷载下自由运动。通过试验测量以及有限元模拟隔震器均可自动向初始位置回复。但由于存在摩擦力,有部分残余位移存在即。
4 工程案例
本案例以5层框架结构,场地设防烈度是6度,场地类别为I,底层层高为4.5 m,2~5层高度均为4.2 m。称重柱形式分别为:700×700 mm与600×650 mm,梁均为300×750 mm。其中1层为第一标准层,2~5层为第二标准层。混凝土等级为C35,整个建筑结构总质量为:6284.545 t。采用有限元软件盈建科对隔震器的实际应用进行分析,模型如图7所示。
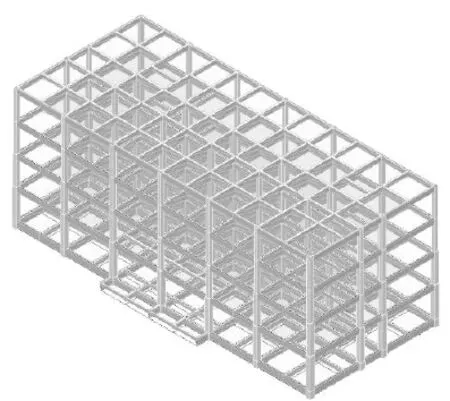
图7 上部结构有限元模型Fig.7 The finite element model of upper structure
选用盈建科软件中的隔震单元模块,具体参数选用表1试验结果所得。地震波从盈建科地震波库中调用适合用于二类场地的Taft(S69)波、EL Centro波和一组人工波。经盈建科软件时程分析所得。

表3 建筑结构的各层间位移、最大位移和剪力Table 3 The displacement, maximum and shearing force between structural layers
表3可知,对于非隔震结构,由于基础与上部结构固接,在任何情况下其位移均为0;其顶层位移为0.064 m,底层的位移为0,所以其相对位移为0.064 m。对于隔震结构,顶层位移为0.04 m,底层位移为0.031 m,其相对位移为0.009 m,其相对位移远远小于非隔震结构,也从另一方面说明隔震器起到很好的隔震效果,是结构整体移动。非隔震结构的最大层间位移是隔震结构的4倍。
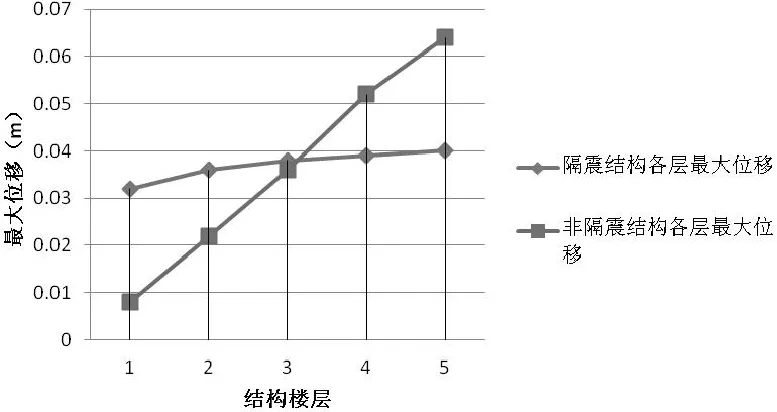
图8 各层最大位移对比示意图Fig.8 Schematic maximum displacement between layers
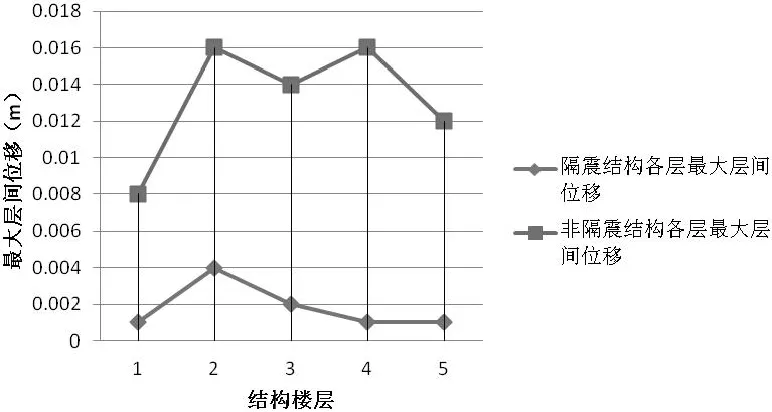
图9 层间位移对比示意图Fig.9 Schematic displacement between layers

图10 层剪力对比示意图Fig.10 The shearing force between layers
非隔震结构基底剪力为6662 KN,采用了新型隔震器结构的基底为1875 KN,相当于非隔震结构的28.1%,层剪力显著减小。在地震作用下,两种结构的基底剪力比值相差1/4。
5 结论
(1)本文提出的新型摆式—滚珠隔震器具有合理的构造,能够很好的隔离水平任意方向地震能量。
(2)通过性能试验研究并结合ABAQUS有限元模型相互印证,新型隔震器的滞回曲线饱满、对称,证明隔震器具有良好的滞回性能和耗能性能。
(3)通过实际工程案例,安装有新型隔震器的结构比未安装隔震器的结构对比分析中得出,新型隔震器具备良好的隔震效果。具有广泛的应用前景。
参考文献
[1]Zayas V,Low S,Mahin S. The FPS earthquake resisting system[R]. Berkeley:University of California at Berkeley,1987
[2]Zayas V,Low S,Bozzo L,et al. Feasibility and Performance Studies on Improving The Earthquake Resistance of New and Existing Buildings Using The Friction Pendulum System[R]. Berkeley:University of California at Berkeley,1989
[3]Zayas VA,Low SS,Mahin SA. A simple pendulum technique for achieving seismic isolation[J]. Earthquake Spectra,1990,6(2):317-333
[4]Mokha A,Constantinou M,Reinhorn A. Teflon bearings in aseismic base isolation:Experimental studies and mathematical modeling[R]. Buffalo,NY:State Univ. of New York,1988
[5]Lin S,Ahmadi G,Tadjbakhsh IG. A comparative study of performance of various base isolation systems,part I:Shear beam structures[J]. Earthquake Engineering and Structural Dynamic,1989,18(1):11-32
[6]Constantinou MC,Mokha A,Reinhorn A. Teflon bearings in base isolation II:Modeling[J]. Journal of Structural Engineering,1990,116(2):455-474
[7]龚健,周云.摩擦摆隔震技术研究和应用的回顾与前瞻(Ⅰ)——摩擦摆隔震支座的类型与性能[J].工程抗震与加固改造,2010,32(3):1-10
[8]周云,龚健.摩擦摆隔震技术研究和应用的回顾与前瞻(Ⅱ)——摩擦摆隔震结构的性能分析及摩擦摆隔震技术的应用[J].工程抗震与加固改造,2010,32(4):1-19
[9]Lu Lyan-ywan,Wang Jain,Hsu Chao-chun. Sliding frequency bearings for near-fault ground motions[C]. Taipei,Taiwan,China:4thInternational Conference on Earthquake Engineering,2006
[10]王建.变曲率滑动隔震防制近断层震波之实验与分析[D].高雄:国立高雄第一科技大学,2006
[11]叶奕麟.摇摆式隔震支承之理论与实验研究[D].高雄:国立高雄第一科技大学,2008
[12]Lu Lyan-ywan,Yeh I-ling,Chang Hsun. Seismic isolators with variable stiffness(SIVS)for earthquakes with strong long-period components[C]. Austin,Texas:ASCE-SEI 2009 Structures Congress,2009:841-849
[13]张季超,李霆,李宏胜,等.新型大直径隔震支座性能检测试验研究[J].建筑结构,2010,8,40(8):31-33
[14]石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006
[15]龚健.新型摩擦摆隔震支座及其隔震结构体系研究[D].广州:广州大学,2010
[16]周云,龚健,邓雪松.变曲率摩擦复摆隔震支座的简化分析与数值仿真[J].工程力学,2012,29(7):163-185层液体传热层。文献[1]研究了直接接触相变传热问题,把相变过程分成三个阶段。两篇文献均分阶段推导了计算模型和求解方法,同时验证了三次多项式热平衡积分法相对于二次多项式、指数热平衡积分法等具有较高的计算精度。
区别于已有文献,本文以第三类边界条件下,长圆柱对流融化过程为研究对象,同时考虑融化后的相变材料被周围流体及时带走,把传热过程分成3个阶段,采用三次多项式热平衡积分方法进行近似求解。最后以冰柱对流换热融化过程为研究对象,分析讨论了冰柱内部各过程的温度分布,以及对流换热系数、冰柱尺寸、冰柱初始温度及水流温度对于相界面移动规律的影响。本文所建立的方法,可以完整的分析第三类边界条件下圆柱相变材料整个融化过程的传热特性,方便的分析显热在各阶段传热特性以及控制参数对于相界面移动规律的影响。
1 物理模型
研究对象为一半径为H的长圆柱,融化温度为Tm,环境温度为θ0,θ0>Tm,对流换热系数为h,圆柱的初始温度为T0,T0<Tm。
本文只讨论如下情形:按照融化时间顺序,融化过程分为3个阶段,如图1所示。第1阶段(图1a),即传热开始至圆柱表面开始融化阶段,从圆柱表面与外界环境之间开始传热为起点(t=0),圆柱边界温度达到融点温度为终点(t=t0),此阶段中温度渗透深度为δ0(t);第2阶段,即圆柱表面开始融化至圆柱中心温度开始上升阶段(图1b),从t1开始,圆柱中心温度开始上升(t=t2)结束,此阶段中温度渗透深度为δ1(t),相界面的位置为H1,当t=t2时,δ1(t2)=0;第3阶段(图c),即圆柱中心温度开始上升至传热结束阶段,从t2开始,圆柱融化完毕(t=t3)结束,相界面的位置为H2。

图1 对流融化过程3个阶段温度分布示意图Fig.1 The temperature profile of convection melting process in three stages
2 求解过程
本文采用三次多项式热平衡积分法对长圆柱内部温度场进行近似求解。该方法是采用三次多项式简单函数来近似描述温度分布的一种方法,且不含二次项三次多项式能更好的反映传热过程的温度场[13]。圆柱内部温度分布方程采用方程(1)形式[1,13]:

其中A,B,C为多项式的系数,可以按照各个阶段的具体条件分别求出。
2.1传热开始至圆柱表面开始融化阶段
在本阶段,圆柱还没有融化。温度渗透深度至圆柱边界范围内([δ0(t),H]))温度发生变化,而其余地方维持在初始温度T0当边界的温度达到Tm时,该阶段结束,时间为t=t1需要说明的是,在温度深度δ0(t)处,假设温度平顺变化,该处存在两个定解条件[13](下文第2,第3阶段中分别出现在δ1(t)和圆柱中心0处)。
圆柱内部导热控制方程,及其定解条件如下:
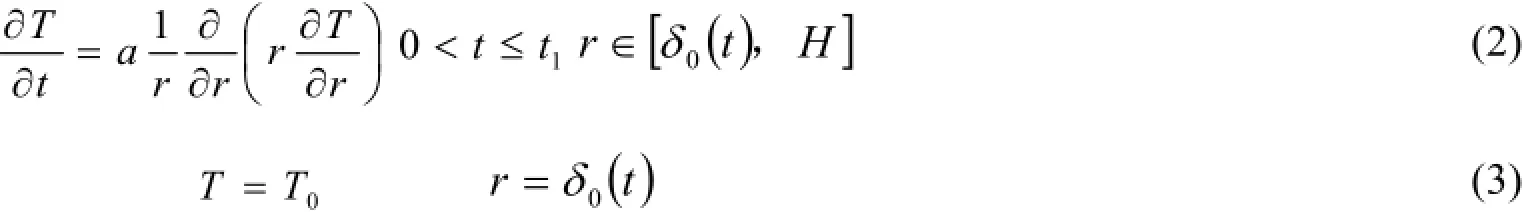

从而圆柱内温度分布可以表示为:


当该阶段结束时t=t1,温度渗透深度为:

2.2圆柱表面开始融化至中心温度开始上升阶段
本阶段,长圆柱表面开始融化,圆柱中心至温度渗透深度([0,δ1(t)]))维持在初始温度,相界面位置为H1当圆柱中心的温度开始上升时,该阶段结束,时间为t=t2。
圆柱内部导热控制方程,相界面能量方程及其定解条件如下:

方程(11)、(12)、(13)分别带入(1)可以得到:
从而圆柱内温度场可以表示为:


方程(10)可以表示为:
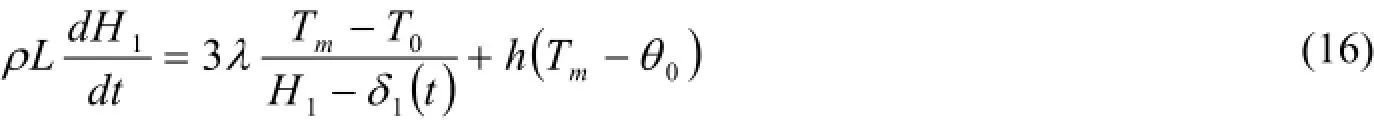
经过上面的转换,方程(9)和(10)转化为易于求解的常微分方程(15)和(16),其中包括两个待求函数H1和δ1(t)。
2.3圆柱中心温度开始上升至传热结束阶段
以上一阶段的结束点t2为开始,至圆柱融化完全为结束,时间为t=t3此阶段温度渗透深度已经达到圆柱中心,且圆柱中心温度不再维持在T0,而是关于时间的函数Tn(t)。
圆柱内部导热控制方程,相界面能量方程及其定解条件如下:

方程(19)、(20)、(21)分别带入(1)可以得到:
从而圆柱内温度场可以表示为:

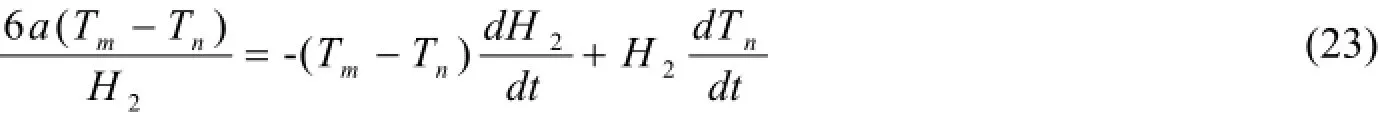
方程(18)可以表示为:

同样经过上面的转换,方程(17)和(18)转化为易于求解的常微分方程(23)和(24),其中包括两个待求函数H2和Tn(t)。
3 分析与讨论
以长冰柱对流融化过程为计算对象,表1为根据文献13所取冰/水的热物性参数值。下文中除了特殊说明的计算数值外,其余均采用表1数值。
在第1阶段,由式(8)可得,t =t1时,当时,温度渗透深度已经达到冰柱的轴心,此时没有第2阶段,这种情况本文由于篇幅问题不予讨论,本文只考虑时的情况。

表1 冰/水参数值Table 1 Parameter values for ice/water
图2为h =763 Wm-2·℃-1融化过程各时间冰柱内部温度分布图。第1阶段整个过程时间约为2.98 s,温度渗透深度较小(5.14×10-3m),此阶段相界面处温度梯度较大,说明此阶段显热交换量较大。第2阶段结束时t2约为92 s,温度渗透至冰柱轴心,相界面位置H1为4.55×10-2m。第3阶段结束时t3=856 s。图中包括了同t2/2(46 s)、t2(92 s)、t3/4(214 s)、t3/2(428 s)及3t3/4(642 s)时冰柱内温度分布图。由图可见,传热开始阶段冰柱内部存在较大梯度,随着融化的进行除了相界面保持温度不变外,其余各点温度均有所上升,在融化后期冰柱内部各点温度趋于一致,并接近于相变温度。
图3为显热量随时间变化图,从图中可见,显热量随时间呈阶段性变化,即第1阶段,该阶段时间非常短暂,且没有发生相变,传热量全部来自显热交换,该阶段显热量相同且最大。第2阶段,显热量迅速下降,t2时显热量约为全部换热量的11%。第3阶段,显热量下降较为缓慢,融化过程后期显热量接近为0。

图2 不同时间冰柱内温度分布图Fig.2 The temperature distribution in icicle at different times

图3 显热量随时间变化图Fig.3 Sensible heat variation the with the time
图4为其他控制参数不变,不同对流换热系数条件下相界面随时间变化图.由图4可见,对流换热系数分别为500、1000、1500及2000 Wm-2·℃-1条件下,相界面随时间约呈线性变化规律,随着对流换热系数的增大,相界面随时间变化率越大(其变化率分别为3.85×10-5、7.69×10-5、1.14×10-4及1.56×10-4m·s-1)。究其原因,对流换热系数越大,水流与冰柱之间的换热量越大,即潜热交换量越大,所以相界面随时间变化率越大。
图5为其他控制参数不变,冰柱厚度分别为0.03 m、0.055 m、0.08 m及0.105 m条件下相界面随时间变化图,从图中可以看出不同厚度条件下,相界面随时间约呈线性变化规律,其变化率基本相同,约为5.88×10-5m·s-1。

图4 不同对流换热系数条件下相界面位置随时间变化Fig.4 Variation of phase interface location with time under the different heat transfer coefficients

图5 不同冰柱厚度条件下相界面位置随时间变化Fig.5 Variation of phase interface location with time under the condition of different pillar thicknesses
图6为其他控制参数不变,冰柱初始温度分别为-5℃、-10℃、-15℃、及-20℃条件下相界面随时间变化图,从图中可以看出不同冰柱初始温度条件下,相界面随时间越呈线性变化规律,随着冰柱初始温度的降低,其变化率越小(其变化率分别为6.25×10-5、5.95×10-5、5.88×10-5及5.68×10-5m·s-1)。究其原因,冰柱温度越低显热所占总换热量越大,潜热交换量所占比例相对较小,所以相界面随时间变化率越小。
图7为其他控制参数不变,外界水流温度分别为9℃、17℃、25℃及33℃条件下相界面随时间变化图,由图可见,不同水流温度条件下,相界面随时间约呈线性变化规律,水流温度越大,其相界面随时间变化率越大(其变化率分别为2.17×10-5、3.95×10-5、5.88×10-5及7.69×10-5m·s-1)。究其原因,水流温度越大越大,水流与冰柱之间的换热量越大,即潜热交换量越大,所以相界面随时间变化率越大。

图6 不同冰柱初始温度条件下相界面位置随时间变化图Fig.6 Variation of phase interface location with time under the different original temperatures on icicle

图7 不同水流温度条件下相界面位置随时间变化图Fig.7 Variation of phase interface location with time under the different water temperatures
4 结论
本文建立了第三类边界条件下长圆柱对流融化过程的分阶段求解方法。获得了各阶段圆柱内部温度分布方程及利于求解相界面移动规律的导热控制方程和相界面能量方程。该方法,可以完整的分析整个融化过程的传热特性,可以方便的分析显热在各阶段传热特性以及控制参数对于相界面移动规律的影响。以长冰柱对流融化过程为研究对象,分析了各控制参数对于相界面移动规律的影响。在本文的计算工况下,通过分析讨论得到结论如下:
2)不同控制参数条件下,相界面均随时间约呈线性变化规律;
3)随着对流换热系数、冰柱初始温度及水流温度的增大,相界面随时间变化率越大,不同厚度条件下,相界面随时间变化率基本相同。
[1]Myers TG,Mitchell SL,Muchatibaya G. Unsteady contact melting of a rectangular cross-section material on a flat plate[J]. Physics of Fluids,2008,20(10):1-12
[2]杨莺,梁艳南,周孑民,等.壳管式相变蓄热器传热效率研究[J].热科学与技术,2011,10(3):226-230
[3]汪玺,袁艳平,邓志辉,等.相变蓄热水箱的设计与运行特性研究[J].太阳能学报,2014,35(4):670-676
[4]莫冬传,吕树申,何振辉.相变蓄冷换热器的优化设计[J].工程热物理学报,2015,36(1):175-178
[5]Ei-genk MS,Cronenberg AW. Solidification in a semi-infinite region with boundary conditions of the second kind:An exact solution[J]. Letters in Heat and Mass Transfer,1979(6):321-327
[6]Gupta SC. The Classical Stefan Problem:basic concepts,modelling and analysis[M]. North-holland:JAI Press,2003:78
[7]贾力,方肇洪.高等传热学[M].第2版.北京:高等教育出版社,2008:90
[8]Cheng kc,Inaba H,Gilpin RR. Effects of natural convection on ice formation around an isothermally cooled horizontal cylinder[J]. Journal of Heat transfer,1988,110(4):931-937
[9]Pedroso RI,Domoto GA. Exact solution by perturbation method for planar solidification of a saturated liquid with convection at the wall[J]. International Journal of Heat and Mass Transfer,1973,16(9):1816-1819
[10]陈则韶.求解凝固相变热传导问题的简便方法—热阻法[J].中国科学技术大学学报,1991,21(3):69-76
[11]Savino JM,Siegel R. An analysis of the transient solidification of a flowing liquid on a convectively cooled wall[C]//Proceedings of the Third International Heat Transfer Conference. USA:NewYork,1962:123-127
[12]Ho CD,Yeh HM,Wang WP,et al. Cool thermal discharge obtained with air flowing over melting ice by complete removal of melt[J]. International Journal of Heat and Mass Transfer,2000,27(6):785-794
[13]Myers TG,Mitchell SL,Muchatibaya GA. Cubic heat balance integral method for one-dimensional melting of a finite thickness layer[J]. International Journal of Heat and Mass Transfer,2007,50(25):5305-5317
ExperimentalResearchonTilting-ballIsolatorandNumericalSimulation
TIAN Zhi-chang1,CAI Jie-feng1,FAN Lie-biao2,ZHAO Gen-tian1
1. College of Architectural and Civil Engineering,Inner Mongolia University of Science and Technology,Baotou 014010,China
2. Inner Mongolia Baotou Municipal Seismological Bureau,Baotou 014010,China
Abstract:This paper studied on the mechanical performances and numerical simulation of a new type tilting-ball isolator under a low cyclic load. The results showed that the hysteresis curve was normal and had a good shock isolation and auto-response performance. Simulation built from software ABAUES was identical with experimental results. The structure with a shock isolator had the better isolation than that without shock isolator through the comparison of 3D models built by finite element software.
Keywords:New type Tilting-ball isolator;performance test;numerical simulation
中图法分类号:TU352.1+2
文献标识码:A
文章编号:1000-2324(2016)03-0437-04
收稿日期:2014-10-22修回日期:2014-10-26
基金项目:国家自然科学基金项目(51268042)
作者简介:田志昌(1961-),男,教授,主要从事工程防灾减灾方面的研究. E-mail:330276700@qq.com

