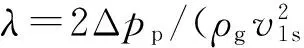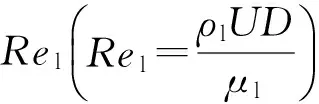湿法脱硫喷淋塔内文丘里棒层构件流体力学
王鹏辉, 庄黎伟, 张 强, 戴干策
(1.华东理工大学化学工程联合国家重点实验室,上海 200237;2.上海天晓环保工程有限公司,上海 201114)
湿法脱硫喷淋塔内文丘里棒层构件流体力学
王鹏辉1,庄黎伟1,张强2,戴干策1
(1.华东理工大学化学工程联合国家重点实验室,上海 200237;2.上海天晓环保工程有限公司,上海 201114)
摘要:在冷模实验观察测定基础上,采用Euler-Euler多相流模型对湿法脱硫(WFGD)喷淋塔内文丘里棒层进行数值模拟,得到不同操作条件下压降和持液量的变化规律。结果表明,棒层区域阻力系数λ分别与和成线性关系(Reg,Rel分别为气相雷诺数和液相雷诺数),持液量H分别与和成线性关系。加入棒层可显著提高持液量,降低液气比(液气体积比为Vl/Vg),此举有利于压降减小。拟合结果对于工程应用有指导意义。
关键词:数值模拟; 喷淋塔; 文丘里棒层; 压降; 持液量
湿法石灰石-石膏烟气脱硫工艺中,喷淋塔得到了广泛应用[1-2]。喷淋塔一般为空塔,液相在塔内经喷嘴分散成液滴与气相接触。空塔内液相分率较低,仅1%~2%,气液两相接触面积有限,为保证塔内传质效果,需提高气相停留时间,且要求气相流速较低。由于流速低,并在大量烟气条件下,喷淋塔体积庞大,直径达5~10 m。在塔内添加内构件可以提高持液量,改善塔内气液两相接触。对此有必要进行详细研究。
林永明[3]、朱敬等[4]测定了不同操作负荷下未加构件空塔内的压降变化,都表明压降随气体速度和液体流量的变化显著,压降与气相速率呈平方关系,与液相流量呈线性关系。塔内压降的主要来源是液滴喷淋的阻力效应,单气相压降几乎可忽略不计。本文引入文丘里棒层内构件,分析其中压降机理,并与空塔进行比较。
本文所用文丘里棒层构件是Ducon公司1976年提出的棒层[5]的改型,其结构是两排呈正三角形的圆柱形棒层(如图1),置于距离入口一定高度位置的塔截面上,流体绕流通过棒层。这类绕流在管壳式换热器壳方流动中十分常见[6],可应用作高温蒸汽的冷凝管束[7-8],但在塔内作为改善均布和强化气液接触效率的构件,研究尚少,在目前文献中仅有定性描述[9-11]。本文通过冷模实验结合数值模拟,分析与研究了喷淋塔内文丘里棒层的流体力学性质。同时,区别于Michalski的曳力平衡理论[12-14],本文将从不同角度探讨过程机理。

图1 文丘里棒层
喷淋塔内液相体积分率较低,因而模拟方法普遍采用离散颗粒群方法(Discrete Parcel Method,DPM)方法。文献[3,15-16]均采用该模型对喷淋塔内的流场进行数值模拟,研究塔内的压降、温度以及浓度的影响,但对喷淋塔结构的工程问题未曾提及。文献[17-19]以DPM模型为基础,通过UDF添加传质方程,同时采用动量源项和壁面函数的方式,考察导流环内构件及除雾器的阻力对流场的影响。
虽然对普通喷淋塔的数值模拟已有一定的报道,但对添加棒层的喷淋塔内流体力学行为至今鲜有任何实质性研究,以及有数值模拟的探索。离散相DPM方法在普通喷淋塔中是合适的,但在加入内构件后,塔内的局部区域持液量较高,两相间相互作用强烈,并且在内构件区域附近的液相已不完全为液滴,DPM模型不再适合。Dudek[20]在研究B&W公司开发的脱硫喷淋塔内添加无溢流筛板内构件时,采用Euler-Euler双流体模型。在双流体模型中,两相相互穿插,分别由各自的连续性方程和输运方程表示,两相间的相互作用通过界面实现。这种方法避免了DPM方法在液相体积分数较大区域的局限性,同时能更准确描述此处两相流行为。实验观察发现在棒层区域持液量较大。因而文丘里棒层(以下简称“棒层”)区域作为主要研究区域时,Euler-Euler双流体模型显然更为适合。Euler-Euler方法在局部采用相分率形式表达各相含量,而两相相互作用需要另外给定。对于本文来说,空塔区域和棒层区域的两相作用需要各自给定。
1冷模实验
实验所有文丘里棒层如图1所示,置于有机玻璃实验装置中观察流型,设备如图2所示,入口处采用铁皮管方接圆方式由长方形入口进入塔体。风系统由4-72型离心风机供给风量(上海金蓝机电设备成套有限公司,流量2 664~5 868 m3/h,全压1 578~989 Pa)。筒体下方液体进入储水槽,水槽内液体经水系统循环至塔顶,经单个螺旋喷嘴(316L不锈钢喷嘴)喷淋进入塔内,水系统由管道泵(浙江大福泵业有限公司,流量25 m3/h,扬程20 m)进行水循环,流量由转子流量计测量。气速在塔顶采用热线风速仪测定。塔内各段压降如表1(测压点P1,P2各距棒层上下表面60 mm)所示。表1中v1为气相速度,Vl/Vg为液气体积比,Δpp为棒层段压降,Δps为喷淋段压降,Δpt为全塔压降。

图2 实验设备的实物图与示意图
在不同气相速率和液相喷淋量下测定塔内各段压降。棒层区域的高度(224 mm)与喷淋区域高度(1 800 mm)比值为1/8,但棒层区域的压降与喷淋区域压降比值为0.36~0.81,棒层区域的压降是同等高度喷淋区域压降的3~6倍。
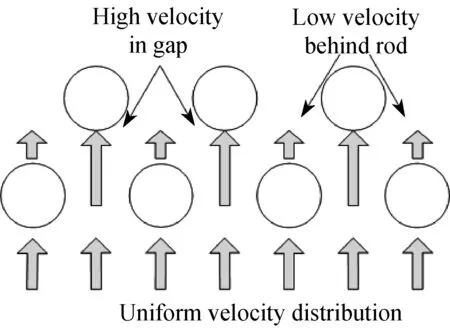
观察发现:空塔区域液滴稀疏,而棒层区域有大量液体聚集,两相间相互作用强烈,且液相有多种存在形式。在文丘里棒上,呈溪流或液膜形式沿棒绕流下落;在棒间隙依然为液滴形式,但气流局部高速使液滴相分率增大。

表1 有棒层构件的喷淋塔压降
2模型基本分析
液滴下落受到气相曳力作用,经短时间的发展,液滴即得以受力平衡(式(1))。当液滴在塔内呈匀速或静止状态时,若不考虑气相与塔壁面的摩擦阻力损失(前文中已叙述单气相压降值可忽略不计)以及对模型做出适当的简化后,根据牛顿第三定律,气相阻力即来自于液滴所受曳力的反作用力。因此,气相在某个区域所受阻力即为此处液滴所受曳力总和(式(2),其中N为单位高度塔空间的液滴数目,y为塔高度)[14]。
(1)
(2)
上述Michalski模型适用于空塔中液相分率较低且均为液滴,但棒层区域气、液两相接触工况与此有很大偏离,需要改变对问题的分析思路,采用新的模型。
通过类比,可将棒层区域视为填料塔段。将棒层区域气相压降分为有、无液相两种情况,即干塔和湿塔两方面考虑,因流体行为主要是单气相和两相的绕圆管层的流动,采用局部阻力表达式(3)分析压降:
(3)
其中:阻力系数采用λ表示,在干塔条件下,λ仅与气相速率有关;湿塔条件下,λ则同时与气相速率和液相流量相关[21]。
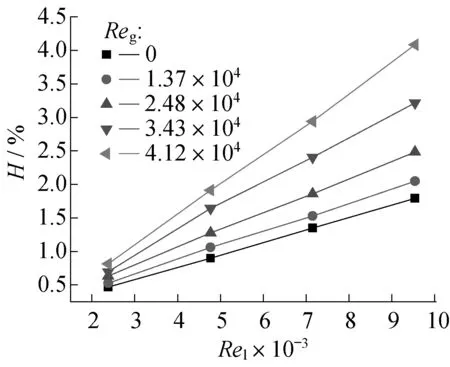
与压降类似,液相在塔内的持液量也可分为塔内气相静止和气相运动两方面考虑,持液量H由区域内液相体积分率表示。气相静止时H仅与液相喷淋量有关,气相运动时,H同时与气相速率和液相流量相关。
利用填料塔的分析形式,可以通过数值模拟研究操作条件对棒层区域压降和持液量的影响,并找出其定量关系。
3数值模拟
3.1计算区域
本文研究三维喷淋塔模型,其几何构型如图3所示。烟气入口尺寸3.2 m×1.6 m,喷淋塔塔径4 m,文丘里棒层位于入口上方2 m,距喷淋层高度1.8 m。棒直径120 mm,棒间距为两倍棒直径。本文主要研究文丘里棒层区域的流场、压降和持液量,故简化计算区域为浆液池上液面至最下层喷淋层。

图3 喷淋塔数值模拟几何结构(单位:mm)
3.2基本假设
为着重研究棒层区域压降、持液量等流体力学问题,简化其他问题,作以下假设:
(1)气体为低速流动,视为不可压缩流体。
(2)忽略塔内喷淋管对流场的影响,同时由于液滴离开喷嘴后很快达到平衡[14],平衡后液滴竖直下落,以此为据,作为近似,认为液滴竖直下落。
(3)假设液滴为球状,暂不考虑塔内液滴的聚并和破碎行为。
(4)气相由空气表示,液相由纯水表示。
(5)暂不考虑塔内传热和传质及其对流动的影响。
根据液滴受力平衡情况及临界韦伯数(Wecr=5.48)联立计算[22],得到塔内液滴的临界液滴大小为dcr=2.4 mm,以该值进行计算。
3.3数学模型
3.3.1多相流模型在Euler-Euler双流体模型中,气液相由各自的连续性方程表示为
(4)
不涉及传质和反应,故相间传质项和反应源项忽略,连续性方程简化为式(4)的形式。其中n为1和2时分别表示气相和液相,α为相体积分率。
气液相运动方程表示为
(5)
不涉及传质,故相间传质引起的动量传递项忽略,方程简化为式(5)的形式。其中-αnp+·τn,αnρng为各相引起动量变化的压力项,剪切力项及重力项、R为气液相间作用力。
在空塔区域,气液两相的作用力主要来自于相间作用力——曳力,表示为
(6)
其中K为相间动量交换系数,由式(7)表达:
(7)
其中f和τ2分别为液滴曳力函数和松弛时间,由式(8)、式(9)定义:
(8)
(9)
根据SchillerandNaumann模型[23],曳力系数CD在Red<1 000时为式(10),在Red>1 000时为式(11)。
(10)
CD=0.44
(11)
其中Red数由式(12)定义:
(12)
根据操作条件估算塔内雷诺数远大于1 000,选择曳力系数为0.44进行计算。
在棒层区域,棒间隙液相受力与空塔区域相同,与棒层接触的液相附于棒层表面,受重力、棒面摩擦力及气相剪切力作用。气相则同时受棒间隙液滴的曳力和绕棒层阻力作用。绕棒层阻力分为压差和摩擦阻力,通过压力项和剪切力项表示。
3.3.2湍流模型以塔内气相平均速度及棒直径为特征速率及特征尺度计算气相雷诺数,判断塔内气相流动状态已经为湍流,计算时需要采用湍流模型。液相为离散相,不考虑液滴群对气体湍流的修正[24]。k-ε模型通过湍流强度和湍流耗散率方程使得动量守恒方程封闭。k-εRealizable模型更加地适合于喷淋塔中两相流的湍流情况[17,22]。
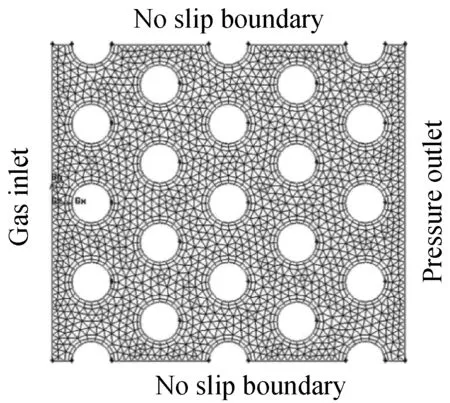
3.4边界条件与计算实施
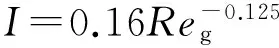
相间耦合为SIMPLE方法,迭代控制方程包括:动量、体积分率、湍流强度、湍流耗散率方程;离散格式均为一阶迎风,各变量迭代松弛因子均为默认值,计算方程残差为10-3。
气相由入口随边界条件加入,由塔顶出口离开。液相由塔顶处设置质量源项Smass,并添加竖直向下的动量源项Smom,使得液滴竖直下落。非稳态计算,通过监控棒层区域及棒层上方区域的相分率变化来判断,计算过程在2 s后基本稳定,取此时的结果进行分析,数值模拟研究的操作条件范围为0 3.5网格无关性分析 计算几何的离散化与计算结果的准确程度关系密切。网格的划分一是方式需合理,二是数量需合理。对计算域进行了3种疏密程度的网格划分,全计算域体积约88.38 m3。棒层区域网格重点考察,各棒表面绘制边界层(如图4),捕捉棒上液相持液量、气相绕流及尾涡行为。棒层区域上方0.4 m内网格节点间距为其余塔体区域的一半。棒层区域与其他区域用interface边界条件分隔。 图4 不同网格密度下棒层区域网格划分 基于合理网格划分,对网格疏密进行无关性分析,划分网格数分别为:(a) 428 840;(b) 1 450 400;(c) 742 984。在v1=5 m/s,L=900 m3/h的操作条件下,对棒层区域上方0.4 m处沿X方向上的持液量及气相速率分布作图,见图5。 图5中,c网格和b网格结果近似(误差均在10%以内),a网格有较大偏差,无法正确模拟。为节省计算量,选择c网格作为计算网格。 图5 网格无关化比较 3.6模拟验证 将模拟结果与经验公式以及实验结果进行对比,气相绕流通过错排管束,参考二维条件下文献[6]中经验关联式,模拟所用工况均在适用雷诺数范围内,建立二维几何模型如图6所示(圆直径、排布方式与文中棒层区域一致,上下平面为无滑移壁面,左边为速度入口,右边为压力出口),模拟出入口两端压降,与经验值对比如表2所示。 图6 单相压降验证几何模型 气液两相逆流通过棒层的过程(气相连续而液相分散),缺乏理论公式与文献实验数据。采用本文所述数值方法,在实验室尺度塔内进行模拟。在v1=1.7 m/s时,不同喷淋密度下冷模实验与模拟压降结果对比如表3所示(两个压降测量点各距棒层上、下表面60 mm)。 表2 气相压降经验计算与模拟结果对比 sim—Simulation result;emp—Empirical result 表3 两相下气相压降实验结果与模拟结果对比(v1=1.7 m/s) sim—Simulation result;exp—Experimental result 单一气相时,气相压降模拟结果与经验计算相比,在低气速下由于绝对值较小,相对误差较大。随着气相速率的增大相对误差减小,模拟值略小于实验值。两相条件下,气相压降模拟结果与实验结果相比两者误差均在10%以内,且模拟值总体略偏小。对比结果表明Euler-Euler多相流方法模拟喷淋塔棒层区域是合理的。 4结果与讨论 4.1概述 根据模拟结果,棒层上表面上方60 mm处及下表面下方60 mm处两平面气相压降差值为棒层区域气相压降。该区域的液相体积分率为棒层区域持液量。 4.2气相模拟 单相流动的阻力研究是多相流研究的基础,分别研究了v1为1,2,3.61,5,6 m/s条件下单气相文丘里棒层区域压降与气速关系,并引入气相雷诺数Reg和阻力系数λ,关系如图7所示。 图7 气相速率与压降v1 (a)以及Reg与λ(b)的关系(单相) 进一步考虑,单圆柱绕流在阻力平方区(104 图8 气相绕棒层流动示意图 从气相绕圆管群的角度考虑,换热器中对于绕二维管群平推流的阻力已有经验公式[6],将通过棒层的阻力系数与经验公式平推流下的阻力系数λ对比,结果如表4所示。 表4 阻力系数λ的经验值与模拟值对比 sim—Simulation result;emp—Empirical result 前文已述,在平推流条件下,二维的模拟结果与经验计算结果相符。但在侧向入口的条件下,流经棒层的流场速率分布不均。结果表明,分布不均将使得通过棒层的平均阻力系数增大,并且在高流速下分布不均现象明显,平推流入口和侧向入口的阻力系数差距更加明显。 4.3液相模拟 图9 液相喷淋量与棒层区域持液量的关系 4.4两相流模拟 4.4.1棒层区域压降及阻力系数在不同的气相速率和液相流量条件下,模拟得到气相通过棒层区域的压降和阻力系数λ,如图10所示。 图10 气相速率与压降(a)以及Reg与λ (b)的关系 由图10可见,棒层区域的压降随着气相速率的增大而增大。干、湿塔压降变化趋势一致,在高液相喷淋量下,压降随气相速率变化更加剧烈。阻力系数λ的变化在湿塔中与干塔不同,λ随气相速率的提高而降低,且在高液相喷淋量下变化趋势更加明显。 棒层区域的压降及阻力系数λ随着液相喷淋量的增大而增大。且阻力系数在低气速下变化趋势更加明显。 气、液相流量对压降的影响敏感程度存在一定差异,气相速率影响更强。液相流量为1 800 m3/h时,气相速率由2 m/s增加至6 m/s,增大2倍,而压降增大420%。而当气相速率为3.61 m/s时,液相流量由900 m3/h同样增大2倍至2 700 m3/h,压降仅增大100%。 随着液相流量的增大,阻力系数λ逐渐增大,表明棒层区域的持液增大了该处的阻力。而随着气相速率的增大,阻力系数λ减小,在Reg大于一定值后λ与Reg无关,近似为常数。 4.4.2棒层区域与喷淋区域压降对比塔内气相压降是设备能耗的重要部分,添加棒层后对塔内压降的影响是衡量其效率的重要标准。本文仅研究最下层喷淋段,但能表达全塔喷淋段与气液相操作参数间的关系。考察棒层区域的压差Δpp与喷淋区域压差Δps的比值,与气相速率的关系如图11所示(干塔条件下空塔段压降相比棒层区域可忽略不计,故不考虑)。 图11 棒层区域与喷淋区域压降比值 由图11可知,Δpp与Δps比值在0.4~1.3之间,即表示加入棒层以后增加的压降倍数。由文献[5]可知,加入文丘里棒层后,产生同样的脱硫效率(>90%),液气比可至少降低一半,在气相速率不变时,则液相喷淋量可减少一半。根据Michalski的压降理论,喷淋段气相压降与液相喷淋量呈线性关系,本文中Δpp也与液相喷淋量呈近似线性关系。这意味着液相喷淋量减少一半,塔内气相压降将减小一半。根据图中所得结果估算,增加棒层后的压降将是原塔压降的0.7~1.2倍,若考虑到实际喷淋塔内喷淋层为3~4层(本文中仅有最下层喷淋层),增加棒层后的压降将会小于原塔压降,则增加棒层有利于压降减小。 另外,Δpp占全塔吸收区域压降比例随气速的增大而增大,随着液相喷淋量的增大而减小。由于棒层区域横截面流通面积仅有空塔区域的50%左右,流速约为空塔区域的2倍,气相速率的影响在棒层区域将更加显著,故随着气速的增大,Δpp与Δps比值将不断增大。而随着液相喷淋量的增大,棒层区域有大量的液滴撞击棒层形成液膜或溪流,对压降的影响不明显,而空塔区域则依然服从Michalski的压降理论,这使得喷淋量的增大对空塔喷淋区域的影响大于棒层区域,从而该比例随喷淋量增大而减小。 4.4.3持液量在不同的气相速率和液相流量条件下模拟得到棒层区域的持液量如图12所示。 图12 液相喷淋量与持液量变化关系 由图12可见,随着气相速率的增大及液相喷淋量的升高,棒层区域的持液量增大。在不同气速下棒层区域持液量变化趋势与气相静止时类似,呈近似线性变化。同时在较大的液相喷淋量下,气相速率对于持液量的影响会更加明显。 相比填料塔来说,棒层区域流动空间较大,固体壁面区域少。液相主要以两种形式存在于棒层区域内,一是液滴形式,其持液量由液滴于棒层区域停留时间决定,液滴受力平衡后,下落速率由气相速率决定,气相速率提高将降低液滴下落速率从而提高持液量。另一种是附于棒层表面的液相,同样也会因为气相速率引起表面剪切力提高而增大持液量。 4.5阻力系数和持液量与操作条件的关联式 4.5.1概述模拟结果表明,压降与持液量均随着气相流速和液相喷淋量的增大而增大。将压降和持液量分别与操作条件进行量纲为一拟合。 4.5.2阻力系数拟合棒层区域阻力拟合得到式(13): (13) 公式适用范围: 1.37×104 2.38×103 4.5.3持液量拟合棒层区域持液量拟合得式(14): (14) 公式适用范围: 1.37×104 2.38×103 阻力系数、持液量的拟合公式的误差值情况分别如图13(a),13(b)所示,由图可知,阻力系数、持液量的模拟值与拟合值误差基本在±15%之内。 sim—Simulation result;cor—Correlation result 5结论 对文丘里棒层区域压降和持液量,在参考填料塔模型基础上,进行了数值模拟,并经实验检验。在研究条件范围内,得到以下结论: (1)Euler-Euler双流体模型描述文丘里棒层区域单相及两相行为是可行的。 (3)棒层的存在对提高喷淋塔持液量有显著作用,研究范围内可以高达4.5%,远高于普通喷淋塔。持液量的增加将有利于喷淋塔脱硫操作液气比的降低。 符号说明: A——喷淋塔截面积,m2 CD——曳力系数 d——文丘里棒直径,mm davg——平均液滴大小,mm dm——液滴大小,mm f——曳力函数 g——重力加速度,m/s2 H——持液量,% I——湍流强度 K——相间动量交换系数,kg/(m2·s2) L——液相喷淋量,m3/h Δpp——棒层区域压差,Pa Δps——喷淋区域压差,Pa Δpt——总压差,Pa R——相间作用力,N/m3 Red——气相绕液滴雷诺数 Reg——气相雷诺数 Rel——液相雷诺数 Smass——质量源项 Smom——动量源项 U——液相喷淋密度,m3/(m2·s) v1——气相速度,m/s v2——液滴速度,m/s v1s——棒间隙气相速度,m/s Wecr——临界韦伯数 λ——总阻力系数 λd——液滴阻力系数 λp——棒层阻力系数 ρ1——气相密度,kg/m3 ρ2——液相密度,kg/m3 α1——气相体积分率 α2——液相体积分率 μ1——气相黏度,Pa·s μ2——液相黏度,Pa·s τ2——松弛时间,s τn——剪切应力,N/m2 参考文献: [1]孙克勤.电厂烟气脱硫设备及运行[M].北京:中国电力出版社,2007,12-17. [2]薛建明,王小明,刘建民,等.湿法烟气脱硫设计及设备选型手册[M].北京:中国电力出版社,2011:25-27. [3]林永明.大型石灰石-石膏湿法喷淋脱硫技术研究及工程应用[D].杭州:浙江大学,2006. [4]朱敬,马强.湿式烟气脱硫喷淋塔内部流场实验研究[J].锅炉技术,2011,42(6):69-72. [5]DuconTechnologies.US-ChinaSOx/NOxTechnicalWorkshop[R].Dalian,China:[s.n.]2005. [6]时钧,汪家鼎,余国琮,等.化学工程手册(上卷)[M].第2版.北京:化学工业出版社,1996:29-32. [7]王银龙,邓科,杨明辉,等.水平管束冷凝换热设计计算问题讨论[J].化工设备与管道,2014,51(3):25-29. [8]刘华,沈胜强,陈石,等.转角正方形管束有降膜流动时的压降实验[J].动力工程学报,2013,33(8):633-636. [9]朱继红,彭卫华.湿式文丘里吸收塔烟气脱硫技术的特点[J].广东电力,2007,20(3):20-22. [10]王新龙,葛介龙,章烨.唐山电厂2X300MW湿法烟气脱硫工程应用[J].电力环境保护,2005,21(4):28-30. [11]戴永阳,蒋春跃,何建华,等.文丘里吸收塔(石灰石/石膏湿法)烟气脱硫技术介绍[C]//中国环保工业协会电除尘委员会:第2届全国脱硫学术会议论文集.南京:电力环境保护出版社,2003:545-549. [12]JACEKAMICHALSKI.Verticalmotionofsphericalparitcles[J].ChemicalEngineeringTechnology,1995,18:434-439. [13]JACEKAMICHALSKI.Two-dimensionalmotionofsphericalparticles[J].ChemicalEngineeringTechnology,1996,19:209-214. [14]JACEKAMICHALSKI.AerodynamiccharacteristicsofFGDspraytowers[J].ChemicalEngineeringTechnology,1997,20:108-117. [15]赵喆,田贺忠,郝吉明,等.颗粒轨道模型用于烟气脱硫喷淋塔两相流数值模拟[J].环境科学,2005,26(6):33-37. [16]赵健植,金保升,仲兆平.烟气脱硫喷淋塔的数值模拟[J].化学工程,2007,35(8):61-64. [17]LUCAMAROCCO,FABIOINZOLI.Multiphaseeuler-lagrangeCFDsimulationappliedtowetfluegasdesulphurisation[J].InternationalJournalofMultiphaseFlow,2009,35:185-194. [18]MONTANESC,GOMEZ-SAMPERA,FUEYON,et al.Computationalevaluationofwallringsinwetflue-gasdesulfurisationplants[J].InternationalJournalofEnergyforaCleanEnvironment,2009,10(4):15-36. [19]WEISSC,WIELTSCHU.Laseropticalflowmeasurementsandcomputationalfluiddynamiccalculationofspraytowerhydrodynamics[J].ChemicalEngineeringResearchandDesign,2005,83(A5):492-507. [20]DUDEKSA,ROGERSJA,GOHARAWF.Compuationalfluiddynamics(CFD)modelforpredictingtwo-phaseflowinflue-gas-deuslfurizationwetscrubber[C]//EPRI-DOE-EPACombinedUtilityAirPollutantControlSymposium.AtlantaUSA:[s.n.],1999. [21]NIKOLAIKOLEV.PackedBedColumns(forabsorption,desorption,rectificationanddirectheattransfer)[M].Netherlands:ElsevierScienceLtd,2006:73-74. [22]ALYHS,ELDRAINYYA,SAQRKM,et al.Amathematicalmodelforpredictingsprayatomizationcharacteristicsinaneulerian-eulerianframework[J].InternationalCommunicationsinHeatandMassTransfer,2010,37:618-623. [23]SCHILLERL,NAUMANNZ.Adragcoefficientcorrelation[J].VDIZeitung,1935,77:318-320. [24]BALACHANDARS,EATONJK.Turbulentdispersedmultiphaseflow[J].AnnualReviewofFluidMechanism,2010,42:111-133. [25]杨纪伟,付晓丽.圆柱绕流研究进展[J].中国水运,2005,8(5):156-158. Flow Behavior through Venturi Rod Banks in WFGD Spray Tower WANG Peng-hui1,ZHUANG Li-wei1,ZHANG Qiang2,DAI Gan-ce1 (1.State Key Laboratory of Chemical Engineering,East China University of Science and Technology,Shanghai 200237,China; 2.Shanghai EnTTention Environmental Engineering Co.Ltd,Shanghai 201114,China) Abstract:Based on the observation and measurement in cold-modelling test,the flow behavior through Venturi rod banks in WFGD spray tower was studied numerically with Euler-Euler multiphase model.The characteristics of pressure drop and liquid holdup under operating conditions were simulated.The results show that resistance coefficient (λ) is proportional to and and the liquid holdup (H) is proportional to and .Introducing rod banks is beneficial to the increase in liquid holdup and the decrease in V1/Vg.The correlation for pressure drop and liquid holdup is instructive for engineering application. Key words:numerical simulation; spray tower; Venturi rod banks; pressure drop; liquid holdup 收稿日期:2015-07-17 作者简介:王鹏辉(1989-),男,江苏常州人,博士生,研究方向为气液两相流数值模拟。E-mail:jaunt_wph@126.com 通信联系人:戴干策,E-mail:gcdai@ecust.edu.cn 文章编号:1006-3080(2016)02-0171-09 DOI:10.14135/j.cnki.1006-3080.2016.02.004 中图分类号:TQ021.1 文献标志码:A