不确定序列子串匹配的概率矩阵算法

段枫凯，吴爱华（上海海事大学信息工程学院，上海　201306）



不确定序列子串匹配的概率矩阵算法

段枫凯，吴爱华
（上海海事大学信息工程学院，上海201306）

摘要：

关键词：

0　引言

字符串匹配问题是计算机科学中最古老、研究最广泛的问题之一。一个字符串是指定义在有限字母表∑上的一个字符序列，而子串就是一个字符串，它是一个长序列的子序列并且任意两个相邻的字符之间没有间隔。例如：在序列w=ACDAB中，AC就是其子串之一，AD则不是，因为AD之间被C隔开。

字符串匹配问题在众多应用中都有着十分重要的作用。例如，生物信息学、信息检索、拼写检查、语言翻译、数据压缩、网络入侵检测、数据挖掘和模式匹配等应用。在现有的研究中，大部分都是对确定序列子串匹配的研究，关于不确定序列的子串匹配的研究较少，而后者的应用需求逐渐增大，比如射频识别测量、轨迹测量和蛋白质在DNA序列中的结合等应用。因此，对不确定序列的子串匹配的研究是十分有意义的。不确定序列是相对于确定序列而言的，例如，上面提到的w= ACDAB就是一个长度为5的确定序列，其字符来源于字符集∑=｛A，B，C，D｝。当w的每一位都不确定，即每一位可能是字符集∑中的任何一个字符时，w便成为了一个不确定序列。如表格1所示，S就是一个长度为8，字符来源于字符集∑=｛A，C，G，T｝的不确定序列。

本文将首先介绍解决不确定序列子串匹配问题的两个算法：可能域算法和简单的概率算法，并对两个算法进行分析，找出简单概率算法的计算结果会出现偏差的原因。接着根据该原因提出一个新算法——概率矩阵算法，并对其进行算法的介绍和分析，最后通过实验验证其正确性和时间复杂度。

1　相关工作

定义1不确定序列：已知一个字符集∑=｛δ[1]，δ [2]，…，δ[c]｝和一个序列S=｛s[1]，s[2]，…，s[n]｝，若满足：

条件（1）s[i]=δ[j]（1≤i≤n，1≤j≤c）；

例1如表格1所示，S是长度为8的序列，∑=｛A，C，G，T｝为字符集。S每个位置可能出现的字符可以是∑中的任何一个字符，满足条件（1），且每个位置可能出现字符的概率之和为1，满足条件（2），因此S是一个长度为8的不确定序列。

表1　长度为8的不确定序列

定义2不确定序列的子串：已知字符集∑=｛δ[1]，δ[2]，…，δ[c]｝和两个序列s、q。s=｛s[1]，s[2]，…，s[n]｝是包含n个字符的不确定序列，q=｛q[1]，q[2]，…，q[m]｝是包含m（＜=n）个字符的确定序列，且两个序列的字符都源于字符集∑。若满足条件q[i]=s[i+k]（0≤k≤n-m，1≤i≤m），则称q是不确定序列s的子串，记为q∈s，记q是不确定序列s子串概率为P（q∈s）。

例2接例1，q= AC时，不确定序列S可能出现的序列有48种情况，当S为ACAGTAGG、GCACTAAA等包含AC且AC之间没有其他字符间隔的情况时，q则为AC的子串。

1.1可能域的方法

可能域方法是解决不确定序列子串匹配问题最直接，同时也是最耗时的算法。可能域方法介绍如下。

例3已知一个不确定序列s如表2所示，根据可能域的定义可以得到其所有的可能域以及可能域的概率如表3所示。

表2　长度为4的不确定序列

很显然，当用可能域的方法计算不确定序列子串匹配的概率时，只需要把所有包含子串的可能域的概率相加即可。

例4接例3，求不确定序列s中，子串q=AC的概率，则：

表3　序列s的所有可能域以及其概率

P（q⊆s）=P（W2）+P（W3）+P（W4）+P（W5）+P（W6）+P （W7）+P（W8）+P（W9）+P（W10）+P（W11）+P（W12）=0.19

可能域方法计算不确定序列子串匹配的概率时，步骤简单，易于理解，计算结果正确，但是其可能域的数量为cn，算法时间复杂度为O（tn），随着n的增大，将算法编程进行运行时消耗时间太长。

1.2简单的概率方法

简单的概率方法解决不确定序列子串匹配的问题时，时间复杂度比可能域算法小的多，可以求得近似值，详细描述如下。

在公式（1）中，s是长度为n不确定序列，q是长度为m（≤n）的子串，其原理为在s中，可能出现n-m+1种情况有连续的m位是子串q而不管其他位是什么，然后再将这n-m+1中情况的概率相加。

例5同例4，计算不确定序列s中，子串q=AC的概率。

运用公式（1），P（q⊆s）≈P（s[1]=q[1]）*P（s[2]=q[2]）+P（s[2]=q[1]）*P（s[3]=q[2]）+P（s[3]=q[1]）*P（s[4]=q[2]）= 0.2。

表4　简单概率方法可能出现的情况

计算完成之后结果为0.2，比用可能域方法计算的结果0.19偏大，原因是如图表4所示，用该方法计算时，共可能出现3种情况，其中？表示可以是字符集中的任何一个字符，那么，情况1和情况3都会有包括ACAC的情况出现，即ACAC的情况被多加了一次，如果减去这种情况的概率一次（由表3可看到出现ACAC的概率为0.01），得到0.19，则与可能域方法计算的结果一致。

简单的概率算法在计算不确定序列子串匹配的结果时，时间复杂度为O（n），但是只能算近似值，随着n的增大，其精确度会原来越差。根据简单的概率算法造成偏差的原因，本文提出了一个概率矩阵的算法，其原理为在不确定序列s中，可能出现n-m+1种情况有连续的m位是子串q而不管其他位是什么，从第一种情况逐渐往第n-m+1种情况计算，并且在计算每种情况的同时，减去前面所有可能与它发生冲突的可能的子情况的概率。

2　概率矩阵算法

2.1概率矩阵算法详细描述

概率矩阵算法分为四个步骤，分别为求重复子串的长度、求子串的行标数组、求概率矩阵和根据概率矩阵求和。

（1）求重复子串的长度

定义4重复子串：已知两个确定字符串q=｛q[1]，q [2]，…，q[m]｝和r=｛r[1]，r[2]，…，r[t]｝（t≤m&&m％t==0），如果满足r[j]=q[j]=q[j+t]…=q[j+（m/t-1）t]（1≤j≤t），则称r是q的重复子串，其长度为|r|=t，且重复次数为m/ t。

例6已知两个序列q=ACACAC，r=AC，则根据以上定义可知，r就是q的重复子串，其长度为2，重复次数为3。

求重复子串长度的伪代码：

Input：m //子串q的长度

Output：t //重复子串的长度

1：t←m //t初始化为m

2：for i←m；i＞1；i←i-1 do //i为重复子串可能的重复次数

3：If m％i == 0 then //满足这个条件可能找到重复子串

4：t←m/i

5：flag←true //用来判断是否找到正确的重复子串

6：for j←t+1；j＜=m-t+1；j←j+1 do //j为和第一个重复子串匹配的子串的第一个下标

7：If！isMatch（1，j，t）then //和第一个重复子串匹配失败

8：t=m

9：flag=false

10：break

11：if flag==true then//所有重复子串和第一个重复子串匹配成功，找到重复子串

12：break

13：return t

求重复子串长度的伪代码如上。其详细过程为，给定一个确定的字符串q，长度为m，其重复子串的重复次数i就可能为1，2，…，m；然后从m开始判断那个值是正确的重复次数，直到找到正确的重复次数或者判断完毕退出循环。在判断的过程，取q的第一个重复子串分别和后面的重复子串匹配，如果匹配成功，则找到正确的重复次数和重复子串，重复子串长度t=m/i，否则，继续判断下一个重复次数。最后，若判断完毕没找到正确重复子串退出循环，则说明q本身就是一个重复子串，重复了一次，其长度t=m。

（2）求子串的行标数组

对于一个长度为n的不确定序列s和一个长度为m的子串q，q中的每个字符都对应s的一个行标，相应的，q中所有的字符就会对应一个行标数组，先将行标数组求出，为下一步求概率矩阵做准备。

求子串的行标数组伪代码：

Input：q，∑//q是长度为m的子串；∑为字符集数组，顺序按照不确定序列s的行标排列

Output：rows//行标数组

1：rows[1...m]←0 //初始化行标数组

2：for i←1；i＜=m；i←i+1 do

3：for j←0，j＜∑.length；j←j+1 do

4：if q[i]=∑[j]then

5：rows[i]=j

6：break

7：return rows

求子串行标数组的伪代码如上，其详细流程为从1至m循环查找m个字符的行标。在每次寻找行标的过程中，将本次的字符依次与字符集数组中元素匹配，若匹配成功，则找到，否则，继续匹配下一个元素，最后将得到的行标数组rows返回。

例7已知一个不确定序列s如表5所示，和一个子串q=ACAC，根据行标数组的算法，显然可知字符集数组∑=｛A，C，G，T｝。首先将q的第一个字符A和∑中的字符一一比较，得到A为∑的第一个元素，因此第一个字符A在s中的行标为0（行标从0开始）。以此类推，求q其他字符的行标，可计算得q的行标数组rows [1...4]=｛0，1，0，1｝。

表5　规模为6的不确定序列s

（3）求概率矩阵

概率矩阵的求解是四个步骤中最核心的一步，它是一个n-m+1行，m/t+1列的矩阵，n-m+1行表示在不确定序列s中，可能出现n-m+1种可能有连续的m位是子串q而不管其他位是什么，每一行i（0≤i≤n-m）都是为了计算第i行除去会与0到i-1行发生重复情况概率的概率。在每行i的m/t+1列的后面m/t列中，依次存放在第i行下的m/t个重复子串的概率。而在每行的第一列则存放1-0到i-1行会与第i行发生重复子情况的概率。

求概率矩阵伪代码：

Input：s，q，t，rows //s：长度为n的不确定序列，q：长度为m的子串，t：重复子串的长度，rows：行标数组

Output：matrix //（n-m+1）*（m/t+1）的概率矩阵，用二维数组表示

1：matrix[0][0]...matrix[n-m+1][m/t+1]←0；//初始化概率矩阵

2：for i←0；i＜n-m+1；i←i+1 do //计算所有除第一列以外的概率

3：for j=1；j＜m/t+1；j←j+1 do

4：p=1；//p必须是浮点型

5：for k=1；k＜t；k←k+1 do //计算第i行第j个元素的值

6：p←p*s[rows[（j-1）*s+t+1]][（j-1）*s+t+ 1+i]

7：matrix[i][j]=p；

8：for i←0；i＜n-m+1；i←i+1 do//计算第一列的概率

9：matrix[i][0]=1；

10：if i＞=t then

11：k←t

12：for l←i-t；l＞=0；l←l-k do

13：p=1；//必须为浮点数

14：count←

15：for j←0；j＜count&&j＜m/t+1；j←j+1 do

16：p←p*matrix[l][j]

17：matrix[i][0]←matrix[i][0]-p；

18：if l=（i-m）then

19：k←1

20：return matrix

求概率矩阵的伪代码如上所示，该代码分为两部分，第一部分是2-7行：计算矩阵中除第一列以外的数据，第二部分是8-19行：进行计算矩阵中第一列的数据。第一部分，在上文中已经提到每行i（0≤i＜n-m+1）的后m/t列中，存放的是该行对应情况下的m/t个重复子串的概率，每个重复子串的概率为t个字符在s对应位置的概率之和。第二部分，计算矩阵中第一列的数据是最关键的一步，当行号i＜重复子串的长度t时，第一列的概率为1，否则，第一列概率则为1-上面行会与当前行发生重复情况的概率。

例8接例7，求子串q在不确定序列s上的概率矩阵。

根据求概率矩阵的伪代码，首先定义一个（n-m+ 1）*（m/t+1）=5*3的矩阵matrix，其中5代表会有如表6所示的5种情况发生，？代表可以是字符集中的任何一个字符。然后执行伪代码的第一部分，首先计算矩阵的后两列，matrix[i][1]（0≤i＜5）是在表6的第i种情况下，子串q的第一个重复子串AC处于位置s[i+1，i+2]的概率；matrix[i][2]是在表6的第i种情况下，子串q的第二个重复子串AC处于位置s[i+3，i+4]的概率。将计算完毕的后两列的概率存入matrix的后两列。最后执行伪代码的第二部分，计算矩阵的第一列，0和1都小于重复子串的长度2，所以0和1两行第一列值都为1。计算第2行，0行和2行都有可能出现ACACAC？？的情况，所以2行的前两位不能是AC，即2行0列的概率matrix[2][0]=1-matrix[0][1]*matrix[0][1]=0.99。同理，第3行的2、3位不可以是AC，matrix[3][0]=1-matrix[1][1]=0.9。第4行的第3、4位不能是AC，1、2、3和4位不能是ACAC，因此，matrix[4][0]=1-matrix[2][0]*matrix[2][1]-matrix[0][0]*matrix[0][1]*matrix[0][2]=0.98。致此，计算完毕，计算结果如表7所示。

表6　可能出现的n-m+1=5种情况

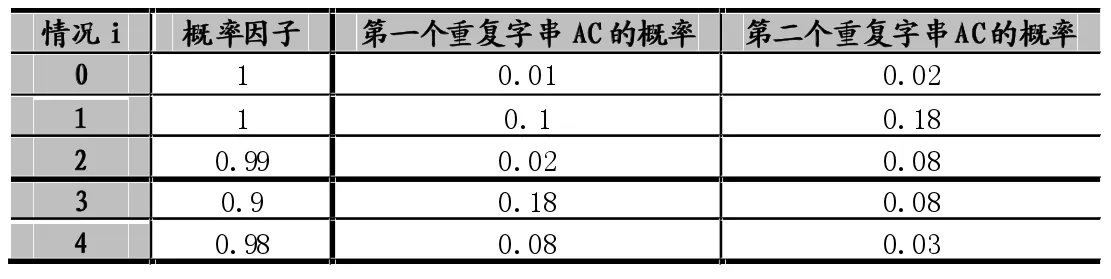
表7　概率矩阵matrix

（4）根据概率矩阵求和

概率矩阵的每行都代表可能会出现的一种情况，因此，当概率矩阵计算结束时，只需要分别将n-m+1行的m/t+1个概率相乘再相加即可。

根据概率矩阵求和的伪代码

Input：matrix //概率矩阵（n-m+1）*（m/s+1）

Output：probability

1：probability←0//初始化概率矩阵

2：for i←0；i＜n-m+1；i←i+1 do

3：p←1//必须为浮点数

4：for j←0；j＜m/s+1；j←j+1 do

5：p←p*matrix[i][j]

6：probability←probability+p；

7：return probability

最后根据概率矩阵求和的伪代码如上所示，其过程为对概率矩阵每行的概率相乘再相加，计算的结果则为最终的不确定序列s匹配子串q的概率。

例9接例8，根据概率矩阵求不确定序列s匹配子串q的概率。

根据伪代码，计算每行的乘积再相加得P（q∈s）= 0.035096。

2.2概率矩阵算法复杂度分析

首先分析概率矩阵算法的空间复杂度。计算重复子串的长度时，占用固定空间的对象是长度为m子串q和重复子串的长度t；占用的可变空间忽略不计。以Java的基本类型字节标准进行计算得子串行标数组的空间复杂度为2*m+4=O（m）。

计算子串行标数组时，占用固定空间的对象是长度为m的子串q，字符集数组∑（假设其个数为c）和行标数组rows（长度为m），占用的可变空间忽略不记，以Java的基本类型字节标准进行计算得子串行标数组的空间复杂度为2*m+2*c+4*m=O（3m+2c）。

求概率矩阵时，占用固定空间的对象有长度为n的不确定序列s（行数假设为c），长度为m的子串q，重复子串的长度t和行标数组rows（个数为m），占用的可变空间忽略不记，以java的基本类型字节标准进行计算得求概率矩阵的空间复杂度为8*cn+2*m+4+4*m=O （4cn+3m）。

根据矩阵概率求和，占用固定空间的对象是上一步得到的（n-m+1）*（m/t+1）的概率矩阵matrix和最后求得的结果probability，占用的可变空间忽略不计，以Java的基本类型字节标准进行计算求得空间复杂度为（n-m+1）*（m/t+1）*8+probability*8=O（m/t（n-m））。

综上所述，概率矩阵算法的空间复杂度为四个步骤之和：O（m）+O（3m+2c）+O（4cn+3m）+O（m/t（n-m）），由于在实际的应用中m、c和t的值非常小。所以，最后的空间复杂度为O（n）。

分析概率矩阵算法的时间复杂度。计算重复子串的长度时，有两层循环，外层循环和内层循环最坏情况执行次数均为m，每次循环基本操作的数量也很小。因此，计算重复子串长度的时间复杂度为O（m2）。

计算子串行标数组时，有两层循环，基本操作执行的次数最多为m*c=O（m）。

求概率矩阵时，第一部分有两层循环，基本操作执行次数为（n-m+1）*（m/t+1）=O（m/t（n-m））；第二部分有三层循环，第一层为n-m+1次，第二层最多执行n-m次，第三层最多执行m/t+1次，因此，基本操作最多执行次数为：（n-m+1）*（n-m）*（m/t+1）=O（m/t（n-m）2）。两部分相加为求概率矩阵时间复杂度的结果：O（m/t （n-m））+O（m/t（n-m）2）=O（m/t（n-m）2）。

根据概率矩阵求和，有两层循环，基本操作执行次数为（n-m+1）*（m/t+1）=O（m/t（n-m）），即求和的时间复杂度为O（m/t（n-m））。

综上所述，概率矩阵算法的时间复杂度为以上四个步骤时间复杂度之和：O（m2）+O（m）+O（m/t（n-m）2）+ O（m/t（n-m））。由于在实际的应用中m、c和t的值非常小，最终的时间复杂度为O（n2）。

3　实验

3.1算法的正确性

首先将可能域算法和概率矩阵的算法用Java语言编程，配置环境为Win7 64位操作系统，Intel Core i3处理器和Eclipse 4.4。然后将不同规模的数据输入进行计算，通过大量的实验，并将概率矩阵算法的结果与可能域方法的结果作对比，证实了概率矩阵算法的正确性。

如表格8-表格10所示，分别为当子串q= ACAC、q= ACGTCAG和q= ACGTACGTA时，在不确定序列s的规模n为10、30、50、100、300、600和1200下两个算法的实验结果的比较，通过观察可以发现随着n的变化，两个算法的结果是相同的，而且不受子串q的长度的影响，其中有一些末位不相同，这是由于Double类型的精度导致的。

表8　m=4时，两种算法求得的结果比较表

表9　m=7时，两种算法求得的结果比较表

表10　m=9时，两种算法求得的结果比较表

3.2算法的时间复杂度证明

通过对概率矩阵算法进行大量实验，获得了不同规模下的运行时间。图1为选取一些数据绘制而成的图，横坐标为不确定序列s的规模n，纵坐标为不同规模数据运行时所消耗的时间，图1描绘了当子串q= ACAC、q= ACGTCAG和q= ACGTACGTA即子串长度m=4、m=7和m=9时，随着n的增大用概率矩阵算法计算耗费的时间图，仔细观察可以发现其曲线趋势和时间复杂度O（n2）相吻合。此外，当q的长度m不同，s的规模不变时，消耗时间相差极小，说明其消耗时间不受子串的长度m的影响。

图1　概率矩阵算法不同长度子串在不同规模下运行的耗时

4　结语

首先介绍了计算不确定序列子串匹配问题的可能域方法和简单的概率方法，然后根据两个算法的比较和分析得出简单的概率算法计算结果会出现偏差的原因，基于这个原因，提出了一个全新的算法——矩阵概率的方法。最后，通过对概率矩阵算法进行分析与大量的实验，证明了矩阵概率算法是正确的，并且其时间复杂度为O（n2），不受子串的长度m大小的影响。

参考文献：

[1]黄建.入侵检测系统中字符串匹配算法与实现[D].华中科技大学，2008.

[2]张宝军.网络入侵检测若干技术研究[D].浙江大学，2010.

[3]刘微.基于生物行为的射频识别系统优化模型与算法研究[D].吉林大学，2011.

[4]韩晓莉.字符串匹配算法在P2P流量检测中的研究与实现[D].北京邮电大学，2007.

[5]聂波.基于流特征的P2P流量检测方法研究[D].北京邮电大学，2009.

[6]C.A GGARWAL，Y.L I，J.WANG，J.WANG.Frequent Pattern Mining with Uncertain Data.in SIGKDD，ACM，2009.

[7]C.C.A GGARWAL，P.S.Y U，A survey of uncertain data algorithms and applications，TKDE，2009.

[8]Y.TONG，L.C HEN，Y.C HENG，P.Y U.Mining Frequent Itemsets Over Uncertain Databases，PVLDB，2012.

[9]L.WAN，C.L ING，C.Z HANG.Mining Frequent Serial Episodes Over Uncertain Sequence Data，in EDBT，2013.

[10]Q.ZHANG，F.L I，K.Y I.Finding Frequent Items in Probabilistic Data.in SIGMOD，ACM，2008：819-832.

[11]Y.X.LI，B.JAMES，K.LARS，J.PEI，Efficient Matching of Substrings in Uncertain Sequences，in SIAM.

Probability Matrix Algorithm of Substrings Matching in Uncertain Sequence

DUAN Feng-kai，WU Ai-hua
（College of Information Engineering，Shanghai Maritime University，Shanghai 201306）

Abstract：

The researches about substrings matching in uncertain sequence are less now.To study possible domain algorithm and a simple probabilistic algorithm，finds the reason of the error of simple probability algorithm，on this basis，puts forward probability matrix algorithm.Describes the probability matrix algorithm in details and complexity analysis，and proves the correctness of the results through programming and comparing with the possible domain algorithm.

Keywords：

目前关于不确定序列子串匹配算法的研究比较少。经过对可能域算法和简单概率算法的分析，发现简单概率算法出现误差的原因，在此基础上，提出概率矩阵算法。对概率矩阵算法进行详细描述和复杂度分析，并通过编程与可能域算法的结果进行比较证明其正确性。

可能域算法；简单概率算法；概率矩阵算法

文章编号：1007-1423（2016）14-0032-07

DOI：10.3969/j.issn.1007-1423.2016.14.007

作者简介：

段枫凯，女，山西人，硕士研究生，研究方向为数据库应用

吴爱华，女，江西人，博士，副教授，研究方向为数据库应用

收稿日期：2016-03-22修稿日期：2016-05-10

Possible Domain Algorithm；Simple Probability Algorithm；Probability Matrix Algorithm